谈五子棋中的数学

朱旭东

摘  要：拉普拉斯认为：“在数学中，我们发现真理的主要工具是归纳和模拟。”恩格斯则以为：“数学是研究现实生活中数量关系和空间形式的学问。”

随着时间的流逝，数学逐渐融入了生活，成为了生活的一部分。“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。”就像中国的爱因斯坦华罗庚先生所说，五子棋盘上也隐藏着数学。

关键词：五子棋盘;坐标;几何

前言：

下棋是棋盘上的战争，下棋的过程中隐藏着一些数学的小心机。你要顾全大局，多方面思考，出其不意攻其不备。根据各棋子的坐標，可以帮助我们分析对方棋路，并以此预判对方下一步棋。同时在下棋的过程中有所发现。

在以下探究中，我们将多方面思考，对一组残局进行研究。探究坐标与棋盘之间的应用，并解决一些关于棋盘的问题。

观察棋盘：

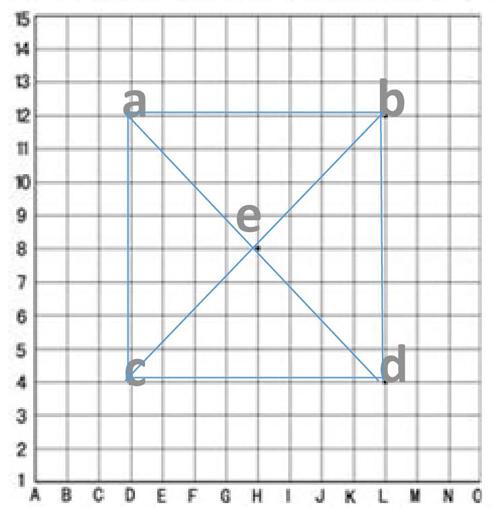
如右图，为一棋盘。棋盘由横纵各15条等距离，垂直交叉的平行线构成，在棋盘上，横纵线交叉形成了225个交叉点为对弈时的落子点。其中直线被称为阳线，而如右图所示由交叉点构成的与阳线成45°夹角的隐形斜线（如：l_cb，l_ad等）为阴线。

观察棋盘，可发现在棋盘上有5个比较特殊的交叉点，这5个点称为"星"。中间的星也称天元。我们设它们为a，b，c，d，e。

如图，a的坐标为（D，12），b坐标为（L，12），c的坐标为（D，4），d的坐标为（L，4），e的坐标为（H，8）。

在下棋时，黑方总是先着棋于天元e，占据棋盘中央的（H，8）相当于包揽了l_ad与l_cb两阴线五子连珠的机会。将五点相连，得一长方形（棋盘上一个小长方形长2.5cm，宽2.4cm）。

由图可知，长方形长为：2.5×8=20（cm），长方形宽为：2.4×8=19.2（cm）

∵长方形的面积=长×宽    ∴S_长方形=20×19.2=384（cm²）

即占据了星和天元后，以天元e为中心面积为384cm²的长方形内五子连珠的机会均为己方所有。

残局对弈：

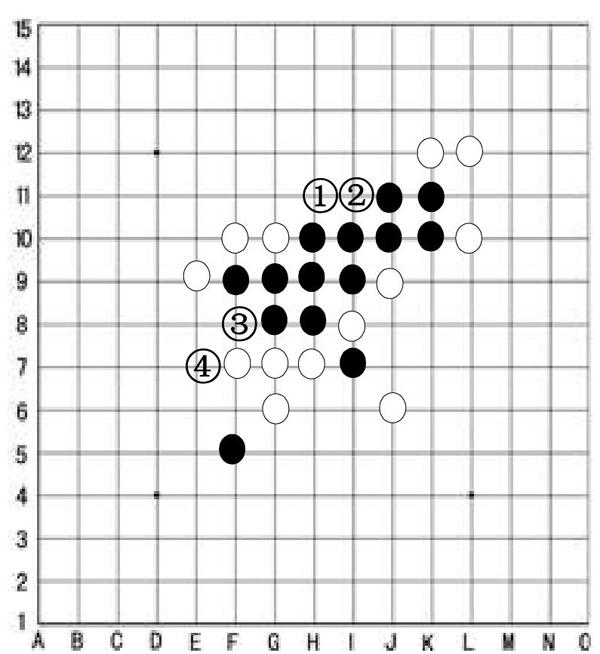
这是一组经典的五子棋残局，可见黑棋主要在以（H，9）为中心集中在一片区域，而白棋则以堵为策，棋路涣散。那么问题来了。

若我方为黑方，对方为白方。问黑方如何落子，可尽快取得胜利？

如图有四种选择，①H，11）②（I，11）③（F，8）④（E，7）

①观察棋局，可发现若下①，黑子立时可完成冲四，如图一。此时为了不使黑子集满五子立即获得胜利。白子必然落子于（H，12），截取所有后路，阻止其冲五。

此时黑方在②着棋冲四，无论白棋在（G，11）堵截还是在（L，11），黑棋只要在两者中一方着子便能获胜。

按其他位置着子，需要下超于2颗棋子。对比之下第一步下①可以更快获得胜利。

拓展提升：

1、在一个平面上，如何用6个围棋子摆出4行，每行3个的图形？

若是要摆出4行，且每行3个，那么一共需要3×4=12个，而一共只能使用6子进行摆放，也就是说1个棋子需要当作2个来用，即一子多用。那么就有多种可能，例如，下图所示的两种方案。

2、除去对称或旋转可以得到的位置，一个棋子在五子棋上有多少种摆法？

比如图中的1号和2号和29号和50号这四个棋子只能算作一种摆法。

我们可以看到这样算的话，五子棋盘有15行，15列。整副棋只需看棋盘的1/2×1/2×1/2=1/8即可，我们以右下角的一半为例来看。（如图二）

即41-49之间的空间39-48及其之间的空间，37-47及其之间的空间，35-46及其之间的空间，33-45及其之间的空间，31-44及其之间的空间，29、43以及最中间天元的位置，那么共有1+2+3+4+5+6+7+8=36种排法。

所以本题的答案是36。

真题实践：

在7×8的长方形棋盘的每个小方格的中心点各放一枚棋子。如果两枚棋子所在的小方格共边或共顶点，那么，称这两枚棋子“相连”。现从这56枚棋子中取出一些，使得棋盘上剩下的棋子没有5枚在一条直线（横、竖、斜方向）上依次相连。问最少取出多少枚棋子才可能满足要求？并说明理由。

第一步证明若任取10个棋子，则余下的棋子必有一个五子连珠，即五个棋子在一条直线上依次相连。利用反证法，假设可取出10个棋子，使余下的棋子没有五子连珠。如图1，在每一行的前五格中必须各取出一个棋子，后三列的前五格中也必须各取出一个棋子，这样，10个被取出的棋子不会分布在右下角的阴影部分。同理，由对称性，也不会分布在其它角上的阴影部分。

第1、2行必在每行各取出一个，且只能分布在（1，4）、（1，5）、（2，4）、（2，5）这些方格。同理，（6，4）、（6，5）、（7，4）、（7，5）所在区域内至少要取出2个棋子。

在第1、2、3列，每列至少要取出一个棋子，分布在（3，1）、（3，2）、（3，3）、（4，1）、（4，2）、（4，3）、（5，1）、（5，2）、（5，3）所在区域。同理，（3，6）、（3，7）、（3，8）、（4，6）、（4，7）、（4，8）、（5，6）、（5，7）、（5，8）所在区域内至少要取出3个棋子。

这样，在这些区域内至少已取出10个棋子。因此，在中心阴影区域内不能取出棋子。由于红色方格的这四个棋子至多被取出2个，从而，从斜方向看必有五子连珠。由此产生矛盾。

第二步构造一种取法，共取出11个棋子，余下的棋子没有五子连珠。如图2，只要取出绿色方格的棋子，则余下的棋子不可能五子连珠。

在7×8的方格中按1、2、3、4、5的顺序依次填入将其编号，可以发现，在该表格中任意一组五子连珠的编号都是1、2、3、4、5各出现一个。其中，56个方格里1出现12次，2、3、4、5均出现了11次。因此，将所有的标号为2的方格中的棋子取出即可（取所有标号为3、4、5亦可）。

结论：最少要取出11个棋子，才可能满足要求。

总结与反思：

（1）反思：在解题的过程中需要在日常下棋过程中观察所积累的经验以及对生活不断的发现，下棋时也需要运用一定的思维能力与空间想象。在生活中运用数学可以让一切变得简单。数学是一种别具匠心的艺术，在棋牌艺术上累计使用，使对弈时，俩者之间更有挑战。

（2）总结：本文在五子棋中寻找数学并通过真题进行实践，完成对坐标思维，列举方法的巩固与应用。事实上，不止五子棋，其他棋牌中也隐藏着很多数学知识。数学家本质上是个着迷者，不迷就没有数学，就无法发现生活中关于数学的种种细节。人们总说细节决定一切，数学家就充分证明了这一点。