基于数学史视角下的双曲线及其标准方程教学设计

陆文婷 韦宏

[摘 要]在数学史视角下可以向我们揭开数学概念、数学思想、数学问题等知识发生和发展的过程。通过数学史融入数学教学，将概念起源和历史向学生展示清楚，不仅可以促进学生对数学概念的深刻认识，而且能把数学文化与教学活动有效结合起来。

[关键词]数学史;双曲线;双曲线方程;数学文化

[作者简介]陆文婷（1999—），女，广西钦州人，南宁师范大学2019级数学与统计学院硕士研究生，研究方向为学科教学（数学）;韦 宏（1968—），男，广西上林人，硕士研究生导师，南宁师范大学数学与统计学院副教授，主要从事学科教学（数学）研究。

[中图分类号] G640[文献标识码] A[文章编号] 1674-9324（2020）45-0-02[收稿日期] 2020-05-14

《普通高中数学课程标准（2017年版）》中明确指出：“数学文化应融入数学教学活动。在教学活动中，教师应有意识地结合相应的教学内容，将数学文化融入教学，有利于激发学生的数学学习兴趣，有利于开拓学生的视野、提升数学学科核心素养。”

在以往的双曲线教学中，学生按照老师的要求直接模仿椭圆概念得出双曲线的概念、标准方程以及性质，但是这样学生并不明白双曲线概念的本质。将数学史融入数学概念教学不仅有利于学生理解数学概念的形成过程，而且能提升学生对数学文化的认同感，彰显数学的育人价值。本文以双曲线及其标准方程的教学设计为例进行分析。

一、教学目标

本节课的教学目标是：一是学生能够理解双曲线的有关概念，掌握双曲线定义的代数形式。二是学生经历分析、归纳、推理和类比的探究双曲线方程过程。三是学生体验数学文化的人文价值和应用价值。

二、数学史融入设想材料选择

圆锥曲线是最先研究为了解决数学“倍立方问题”而引起的。門奈赫莫斯曾经用了两种方法解决了“倍立方问题”，与此也就发现了圆锥曲线。阿波罗尼奥斯在前人的基础上继续研究了圆锥曲线得到了许多圆锥曲线的性质，这些研究成果也就是他的著作《圆锥曲线论》。由于在其著作中关于双曲线的定义正是现在教材中的标准定义及其有关性质的证明符合学生的几何水平，所以本文采用阿波罗尼奥斯的双曲线产生与定义证明的数学史来融入双曲线教学。通过经历历史上对双曲线探索向学生揭示曲线本质，即平面内到定点的距离与定长关系。抓住了本质，学生在探索双曲线时就可以追溯数学定理、法则。本文以数学史融入双曲线概念教学为例，培养学生追溯数学定理、法则能力和解决问题能力，从而在概念教学中渗入核心素养，有助于学生在后续数学的学习起到重要的作用。

三、教学过程设计

（一）复习旧知引入，设置问题驱动

教师引导学生回忆椭圆的定义、标准方程及其性质并提出问题（1）：我们知道椭圆是由一个平面截一个圆锥得到的，有没有其他方式去截圆锥？并引导学生讨论。

师生活动：教师展示平面和圆锥的图片，学生尝试利用图片和空间想象能力找出不同于椭圆的截线并互相交流。然后，教师引导学生将平面与不过顶点且与底面相交的圆锥相截，并得到结论：所截得到的截线不同于椭圆的一个弧形线。

设计意图：复习椭圆的相关知识，可以为后续的双曲线做对比铺垫。学生通过探究截线的过程可以发展他们的空间想象和思维发散能力，同时也让学生明白为什么要学习这个知识，是因为发现圆锥被不同位置的截面可以产生不同的截线。

（二）概念形成，符号定义

1.推广切割，引出概念。教师将问题（1）推广到其他情形，把截一个圆锥改成截两个对顶的圆锥，出示问题（2）。

问题（2）：用刚才的截法去截两个对顶的圆锥会得到什么样的图形？

师生活动：基于问题（1）的做法，教师引导学生将平面与不过顶点且与底面相交的两个圆锥相截得到的截线就是今天要学习的双曲线。

然后，教师指出这种截面得到的图形的方法其实由来已久，并向学生介绍阿波罗尼奥斯的故事和用几何画板展示平面截圆锥的动态过程：

阿波罗尼奥斯对圆锥曲线研究成果写成一本著作《圆锥曲线论》。其中问题（1）中的截线被阿波罗尼奥斯称为超曲线，也就是今天“双曲线的一支”。问题（2）中截线是超曲线，这样的两条截线被称为是“二相对截线”，也就是今天的双曲线。而“双曲线”这个名字是由我国清代数学家李善兰在其著作《代微积拾级》翻译过来的。

设计意图：问题（1）的探究得到了双曲线的一支，问题（2）得到的是今天教材的双曲线。问题探究让学生经历双曲线知识的产生过程，引入数学史是学生体验数学文化的人文价值。借助几何画板来动态向学生展示平面截圆锥得到的双曲线截线，使学生深刻感受双曲线的几何表征。

2.提出猜想，推理验证。问题（3）：对于得到的双曲线，你想研究它的什么？

师生活动：学生模仿已学过的椭圆相关性质来探究双曲线的性质。教师引导学生讨论后，介绍阿波罗尼奥斯研究双曲线的性质并和学生一起证明。

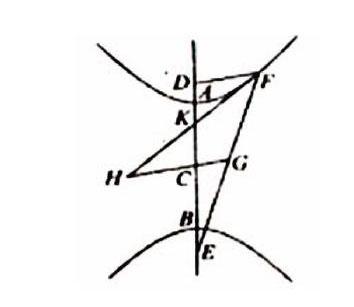
“二相对截线”的轴为AB，中心为C，且矩形AD·DB和矩形AE·EB都等于图形的四分之一，以贴合点E和D到截线上任一点F的连线为EF和FD。且∠KFD=∠GFH。

证明：如图所示，设过F作切线FKH，过C作GCH平行于FD，所以∠KHG=∠KFD;又因为∠KFD=∠GFH，所以GF=GH;因为C为轴AB的中心，所以AC=CB、EC=CD;因为GF=GH、AE=BD，所以GH=EG，所以FE=2GH。又因为已证CH=CB，所以EF=2（GC+CB）;因为FD=2GC，且AB=2CB，所以FE=FD+AB，即FE-FD=AB。

设计意图：教师与学生一起证明得到双曲线上以贴合点E和D到截线上任一点F的连线EF和FD的差是一个定值AB。此证明结果与椭圆定义对比发现都是平面内到定点距离与定长关系的曲线，这也是曲线的本质。学生在椭圆的基础上体验追溯双曲线的定义，在后续的抛物线就顺利追溯出相关定义。

3.概念本质，符号定义。问题（4）：能不能用数学式子表示得到的结论？

师生活动：师生通过类比归纳证明过程与结论共同得到双曲线的定义：把平面内两个定点的距离的差的绝对值等于非零常数（小于F1F2）的点的轨迹方程叫作双曲线。两个定点叫作双曲线的焦点（阿波罗尼奥斯没有给出“焦点”的定义，而把焦点说成是“由贴合产生的”，把它叫作“贴合点”）用数学符号表示：||PF1|-|PF2||=2a（2a

设计意图：教師向学生重构知识的发生，学生体验到数学在发展的过程中数学家经过火热的思考，促进学生对知识的理解。让学生用符号表征概念，有利于树立学生的符号意识，发展数学观念。

（三）双曲线的标准方程

问题（5）：能不能类比椭圆方程推理过程，推理得到双曲线的方程？

师生活动：教师引导学生类似推导椭圆方程一样，建立直角坐标系，并用借助余弦定理和勾股定理探究双曲线标准方程推导。学生合作求出双曲线标准方程后引导学生思考焦点如果在y轴上，得到的双曲线标准方程是？

设计意图：学生经历分析、归纳、推理和类比的探究双曲线方程过程，提升数学核心素养。

（四）巩固练习，加深概念认识

选择一些辨别双曲线定义和求满足某些条件的标准方程（列出具体题目略）

设计意图：利用练习让学生领略数学的美学价值，有利学生理解数学概念的形成过程，提高教学效果完成教学目标，而且能提升学生对数学文化的认同感，彰显数学的育人价值。

四、结语

教师利用数学史融入双曲线教学，通过探究验证过程让学生明白知识的产生与来源，并在探究过程与历史人物的思想产生思维的碰撞，学生可以穿过时间的洪流与历史人物有思维的共鸣。并且在这思维碰撞中培养了学生对数学概念、定理法则的追溯能力与习惯。进而有利于学生理解数学概念的形成过程，能提升学生对数学文化的认同感，彰显了数学的育人价值。

参考文献

[1]中华人民共和国教育部制定.普通高中数学课程标准2017年版[M].北京：人民教育出版社，2018.

[2]Apollonius of Perga，圆锥曲线论（朱恩宽，等，译）[M].西安：陕西科学技术出版社，2007：230-232.

[3]侯代忠，喻平.彰显数学文化：教学设计中的三个自问[J].数学通报，2018，57（9）：32-36.

Teaching Design of Hyperbola and its Standard Equation from the Perspective of Mathematical History

LU Wen-ting， WEI Hong

（College of Mathematics and Statistics， Nanning Normal University， Nanning， Guangxi 530299， China）

Abstract： From the perspective of the history of mathematics， we can reveal the occurrence and development process of mathematical concepts， mathematical thoughts and mathematical problems. By integrating the history of mathematics into mathematics teaching and showing the origin and history of concepts to students clearly， it can not only promote students' deep understanding of mathematical concepts， but also effectively combine mathematical culture with teaching activities.

Key words： history of mathematics; hyperbola; hyperbolic equation; mathematical culture