Research on sliding mode control of manipulator based on RBF neural network optim ized by bionic swarm intelligence
Yu-jia YANG,Fu-quan ZHANG,Yi-ou WANG
(1 Tianhe College of Guangdong Polytechnic Normal University,Guangzhou 510540,China)
(2 School of Computer Science&Technology,Beijing Institute of Technology,Beijing 100081,China)
(3 Beijing Institute of Science and Technology Information,Beijing 100044,China)
Abstract:In order to improve the accuracy of the slidingmode control of themanipulator,the RBF neural network is used to complete the sliding mode control of the manipulator,and the hybrid leapfrog algorithm in the swarm intelligence algorithm is used to optimize themodel parameters.In the process ofmanipulator slidingmode control and manipulator trajectory tracking,theweights and thresholds of RBF neural network are used as frog individuals of the leapfrog algorithm.The frog group is composed of randomly generatedmultipleweights and thresholds,and the frog group is grouped.The global optimal individual is obtained by continuous re-grouping and intra-group iteration,and after the optimalweightand threshold are obtained,the optimal slidingmode controlmodel of themanipulator is determined.The experimental results show that the slidingmode control ofmanipulator based on bionic swarm intelligence optimization RBF neural network has high tracking accuracy.
Key words:Bionic group intelligent optimization,Manipulator slidingmode control,RBF neural network,Leapfrog algorithm,Tracking error
With the development of computer technology,the application of robots is becomingmore andmorewidespread,and the control complexity requirements of robots are gradually increasing.Themanipulator,as the main unit of the control end of the robot,occupies an important position in robot research.In view of the differences in robot tasks,more stringent requirements are put forward for the control accuracy and multi-angle of themanipulator.
In recent years,research on robots has become a hot topic.Many scholars have studied the control of robots from different angles.The coordinated tracking control ofmultiple nodes of themanipulator is studied in Yan M D et al.[1].The movement of multiple nodes uses a distributed motor as the driving force.Themovementof themanipulator in Yu Q etal.[2]is completed by automatic circuit control.The anti-interference ability of the nonlinear manipulator has been greatly improved in Dong X L et al.[3].The detailed motion analysis of the 5R joint of the manipulator is given in Tian F and Mou C J[4],and the key points of the5R jointmotion are proposed.In this paper,the slidingmode control of themanipulator is taken as the research object,and the RBF neural network algorithm is used to realize the slidingmode control of the manipulator.
1 RBF neural network
Let the input sample beXk=(x1,x2,…,xn),k=1,2,…,m,Wherem and n respectively represent the total number of samples and the total number of features of 1 sample.In general,the number of neurons in the input layer is equal to the total number of features.After the sample feature filtering is performed,the number of neurons in the input layer is generally less than the total number of features.The outputof the K-th sample after themodel is:Yk=(y1,y2,…,yn),n is the number of neurons in the output layer.
First,the value of the input sample through the weight to reach the first layer of the hidden layer[5]is shown in formula(1).
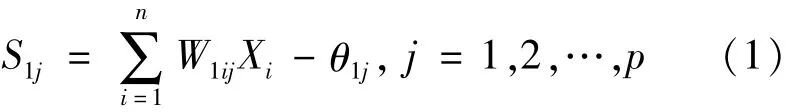
TheS1jvalue can be obtained after the feature conversion function:

The feature conversion function selected by RBF neural network is Gaussian function.Whereσis a real number greater than 0,andcjis the center value of the j-th hidden layer[6].Taking the first hidden layer as input,the value that reaches the second hidden layer after weighting is shown in formula(3).
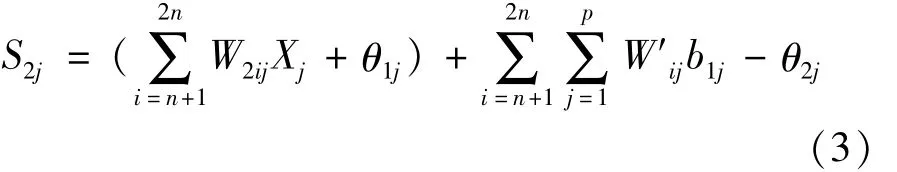
Then the transformation function is solved to get formula(4).
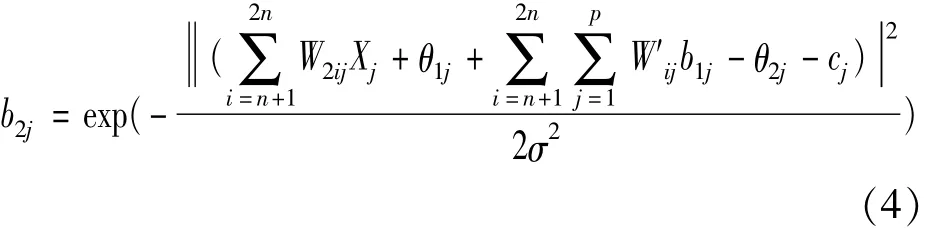
For all hidden layer outputs,the result obtained after weightingVjtis shown in formula(5).

The above formula is solved by Gaussian function to get the output of the entiremodel.
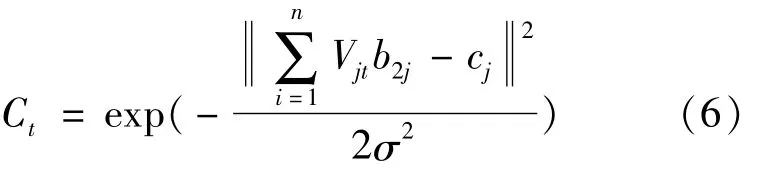
The error result of thek-th sample is shown in formula(7).

The error of all samples is shown in formula(8).

The above formula undergoes first order differentiation to get formula(9).

The weights from the hidden layer are solved to the output layer.Continue to solve the weights of the input and hidden layers.

2 Manipulator sliding mode control
Set the control system[7]as formula(11).

Let sliding surface function[7]iss(x),s∈Rm,then the control function isu.
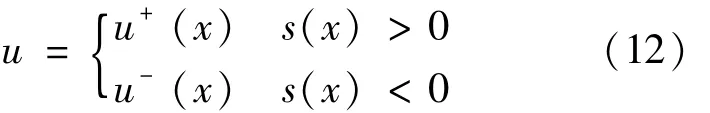
Let the inertial force termM(θ),the centrifugal force termH(θ)and the gravity termG(θ)of themanipulator,then themotionmodel[8]of themanipulator isτ.

The tracking error isE.

Whereθandθdrepresent the actual and target angles of themanipulatormovement,respectively.andrepresent the actual angular velocity vector and the target angular velocity vector of themanipulatormovementrepresents the actual angular acceleration vector of themanipulatormovement.
Then the sliding surface trackingmethod iss.
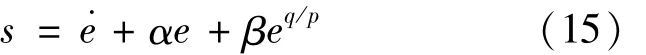
Whereα,β∈R,p>q.
Differentiate formula(15)to get

Let formula(16)be equal to 0,then formula(17)can be obtained.
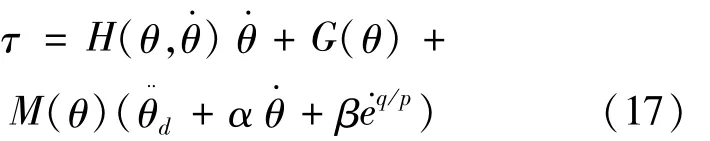
3 Intelligent op tim ization of bionic group
3.1 Leapfrog algorithm
Suppose that there are P frogs in the pond toform a group of frogs,labeledSelect the reciprocal of the tracking error of the robot as the fitness function,calculate the fitness of all frogs,and mark the frogwith the largest reciprocal of tracking error asxg.The number of attributes of the optimization problem iss,and one of its optimal solutions is recorded as=[xi1,xi2,….xis].First,P frogs are randomly divided into M groups,and then themaximum food search is performed in each of the M groups.The movingmethod[9-10]is shown in formula(8).
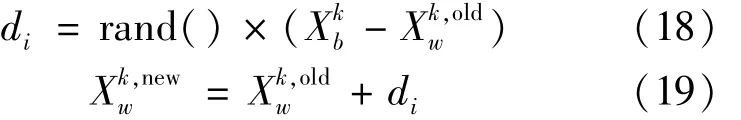
Where,is the best individual in thekgroup,andare theworst individuals before and after the movement in thekgroup,rand()is a random number,anddiis themoving step.
According to the results obtained by formulas(18)and(19),calculateXandXas independent variables to solve their fitness.If the fitness after moving is greater than that beforemoving,itmeans that the position of the worst individual ismoving closer to where food is plentiful.Replacewith,update,compare the fitness ofwithxg,updatexg;Instead,replacewithxg.Then continue to search for the optimal frog of other groups according to equations(18) and (19), and compare withxg, and updatexg.
3.2 RBF neural network optimization of frog jumping algorithm
There are two main ways to optimize RBF neural network.One way is to continuously optimize the weights and weight thresholds of each layer of the RBF neural network through an algorithm[11],and to make the output of the RBF neural network closer to the actual result through weight optimization.Another way is to continuously adjust the number of nodes and node distribution of the RBF neural network through an algorithm,so that the output of the RBF neural network is closer to the actual result.In practice,the two approaches can also bemixed in order to obtain a globally optimal solution.
In this paper,RBF neural network weight and threshold optimization are used as the main optimization approaches.In the optimization process,the frog jumping algorithm is introduced into the RBF neural network.Based on the initialweights and the network model structure generated by randomly preset nodes,the network results aremathematically represented and encoded,and the mathematical representation is in the form of amatrix.The sum thresholdmatrix is used as the input set of the frog jumping algorithm.A network structure model with a smaller error function is selected for algorithm optimization.
The process of the optimal individual obtained by the frog leap hybrid optimization is actually the process of solving the optimal solution of the RBF neural network weights and thresholds[12].With the optimal solution of weights and thresholds,the sliding mode control model of the manipulator of the RBF neural network can be determined.The optimal result of the Leapfrog algorithm training is the optimal RBF neural network structuremodel.
3.3 Manipulator slidingmode control process
According to the optimal RBF neural networkmodel obtained in Section 3.2,inputmanipulatormotion data samples,and obtain the manipulator sliding mode controlmethod after training.In the frog leap algorithm deployment,the entire frog group needs to be continuously grouped,and the positions of individuals with large tracking errors in the group are constantly updated to improve the fitness value of all individuals in the group.The parameter adjustmentmethod of this neural network model is efficient,and each iteration increases the fitness value.
The general flow ofmanipulator slidingmode control of RBF neural network optimized by hybrid frog leap is shown in Fig.1.

Fig.1 SIiding mode contro I fIow of robot hand based on Ieap frog op tim ization RBF neu ra Inetw o rk
4 Sliding mode control sim u lation of m ani-pu lator
In order to verify the performance of frog leap-optimized RBF neural network for manipulator sliding mode control,an example simulation was performed.
Let the target angles of joints1 and 2 beq1d(t)andq2d(t),As shown in formulas(20)and(21),they are derived to obtain the target angular velocities(t)and˙q2d(t),respectively.According toformula(17),we set the basic parameters as follows:α=5,β=3,q=1,p=3.

The RBF neural network algorithm optimized by Leapfrog was used to control the sliding mode of the manipulator,specifically the tracking of themanipulator’s targetmotion.
4.1 Tracking accuracy simulation
The RBF neural network and the RBF neural network through the hybrid frog-leaving algorithm were used to simulate the target angles of the joints1 and 2 of themanipulator respectively,and the tracking error was used as the evaluation standard.In the simulation process,in order tofully verify the impact of frog jump optimization on tracking accuracy,the RBF neural network structure was differentiated and its performance was verified.

Tab Ie 1 Tracking ang Ie error ofm anipu Iato r m o tion track
It can be seen from Table 1 that as the network scale increases,the angular tracking errors of robot nodes 1 and 2 gradually decrease,and the tracking accuracy improves.When the number of neurons in the hidden layer reaches10,the average tracking error degree stabilizes and no longer decreases as the number of neurons increases.Becausewhen the number of hidden layer neurons is 10 and 15,respectively,the maximum error degree of the angle tracking of the two nodes changes little,and the average tracking error no longer changes,reaching stable values of 0.857 2°and 0.947 2°,respectively.
In the following,the trajectory tracking simulation is performed on the RBF neural network that is notoptimized by the frog jumping algorithm and the algorithm in this paper.The number of hidden layer neurons is set to 10,and the error tracking results are shown in Fig.2 and Fig.3.
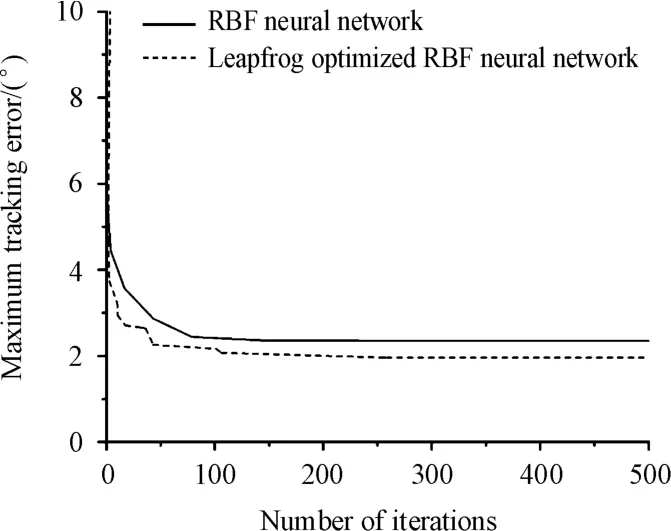
Fig.2 Maxim um ang Ie error of m anipu Iator trajectory tracking based on two a Igorithm s

Fig.3 Mean ang Ie error of robotic trajectory tracking w ith tw o a Igo rithm s
It can be seen from Fig.2 and Fig.3 that under the same neural network scale,themaximum tracking error and average tracking error of the robotic motion of the RBF neural network manipulator based on the Leapfrog optimization are lower,indicating that the tracking accuracy is higher.
4.2 Errors at different tracking trajectory frequencies
In order to verify the impact of the manipulator’s motion speed on the tracking trajectory,the RBF neural network and frog leap optimized RBF neural network algorithm were used to simulate themanipulator’s trajectory at different desired frequencies.The number of hidden layer neurons is 10,and the expected frequency of themotion trajectory is set to 0.3 rad/s,0.4 rad/s,and 0.5 rad/s,respectively.Its tracking performance is shown in Table 2.

Tab Ie 2 Tracking erro r of d ifferen t expec ted trajec to ry frequency
It can be seen in Table 2 that when the expected trajectory frequency of the movement increases,the robot trajectory accelerates,themaximum tracking error and average tracking error of node 1 and node 2 become larger,but the comparison shows that the tracking performance ratio of RBF neural network robot optimized by Leapfrog A pure RBF neural network is better.
4.3 Frog Leaping mixed parameter optimization simulation
In order tofurther simulate the optimization performance of the RBF neural network optimized by the frog leap hybrid,the main parameters of the hybrid frog leap algorithm were simulated differentially.The main purpose is to simulate the number of groups of frog swarms,the step size of frogmovement,and the number of iterations within the group after grouping frog swarms to verify the effects of different parameters on the tracking of the robot’smotion trajectory.The number of neurons in the hidden layer of the RBF neural network is set to 10,and the number of groupings is10,20,30,40,and 50,and the step length is 1,3,and 5.
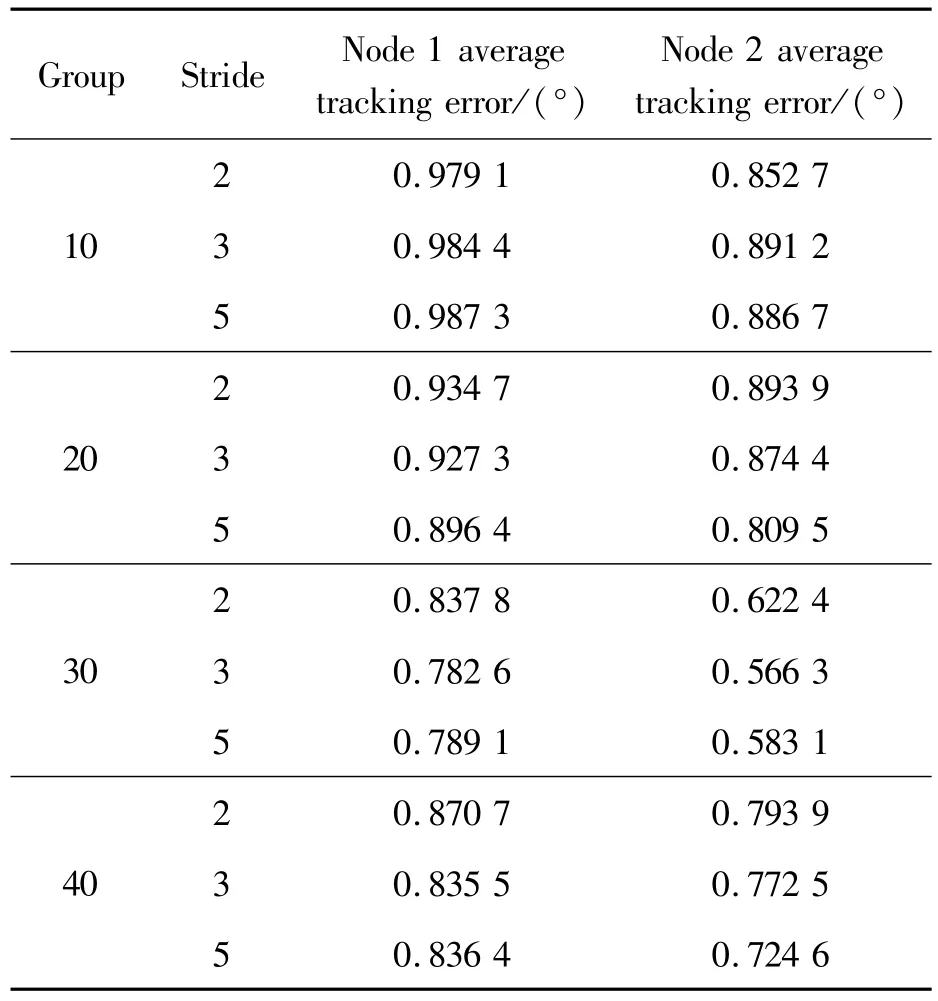
Tab Ie 3 Tracking error of different groups and steps
It can be seen from Table 3 thatwhen the number of packets belongs to[10,20,30,40]and the step size is[2,3,5],the average tracking error of node 1 does not exceed 1.0,and the average tracking error of node 2 Notmore than 0.9.By comparison,when the number of packets is 30 and the step size is 3,the minimum average errors of node 1 and node 2 are 0.782 6 and 0.566 3,respectively.In actual application,the parameters of the frog jumping algorithm can be finetuned by repeatedly changing themain parameter simulationmethod to achieve better tracking results.
In summary,when the number of hidden layer neurons is 10,the number of frog jumping algorithms is set to 30,and the step size is 3,the optimal robot trajectory tracking performance can be achieved.
5 Conclusion
The RBF neural network optimized by the bionic intelligent frog jumping algorithm is used formanipulator sliding mode control with high accuracy,which can improve the tracking performance of the manipulator motion trajectory to the target trajectory.In the actual application process,the scale of the RBF neural network should be set reasonably,and the number and step size of the frog jumping algorithm should be adjusted dynamically in order to achieve the optimal sliding mode control performance of the manipulator.When the movement speed is slow,the trajectory tracking performance is high and the error is low.But when the motion control of the manipulator has time requirements,the applicability of the algorithm will decrease.Therefore,subsequent research will further optimize the time performance of the algorithm to achieve higher tracking accuracy at higher trajectory frequencies.
- 机床与液压的其它文章
- Study on Face detection method based on lightweight convolutional neural network
- Application of genetic optim ization lvq neural network in equipment fault diagnosis system
- Research on bearing fault diagnosis technology based on deep convolution neural network
- Research on the application of improved machine learning collaborative recommendation algorithm in intelligent control
- Design of liquid filling machine positioning system based on RBFneural network activedisturbance rejection controller
- Kinematics and dynam ic performance analysis of a 3-R2H2S parallel robot

