一类NLS方程近似解误差分析

万洲键，龚 祯，牟健生，杨方林

(南京工程学院电力工程学院，南京 211167)

0 引言

很多工程问题都可以转换成非线性方程求解。分数阶方程在社会生活的各个领域应用广泛，因此研究非线性方程的解具有极大意义。至今为止，人们已经找到非线性方程精确解及近似解的各种方法[1-3]。

对于一类NLS方程：

(1)

通过查阅文献[4]得到(1)的精确解表达式如下：

(2)

通过拉式变换迭代法，分析近似解与精确解的数值误差，验证算法的可靠性。

1 定义

卡普托导数

(3)

f(t)的拉普拉斯变换定义为：

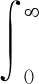
(4)

(5)

2 拉式变换推导近似解

本研究着重误差分析，近似解推导思路如下：

(6)

对该式子两边进行拉氏变换：

(1-x2)u+|u|2u

(7)

(1-x2)u+|u|2u

(8)

对其两边作拉式逆变换得：

(1-x2)u+|u|2u

(9)

取u0=x得：

(10)

(11)

(12)

…

(13)

通过计算，得到系数规律：

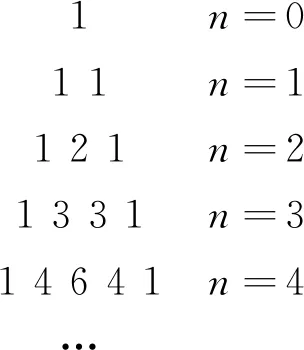
(14)

即第n行系数为：

(15)

3 误差分析与数值结果

为了验证修正Laplace变换迭代法求解结果的有效性，对各级近似解进行误差分析和数值模拟，分别讨论当α=1,β=1时的整数阶方程情形和当α=0.5,β=0.5时的分数阶方程情形。在表1和表2分别给出了整数阶方程和分数阶方程实部和虚部的误差分析数据，在图1～3中分别给出了相关近似解和精确解实部和虚部的立体图和平面曲线图。

表1 当α=1, β=1时，实部和虚部的数值结果Tab.1 Numerical results of the exact and imaginary partswhen α=1, β=1

表2 当α=0.5, β=0.5时，实部和虚部的数值结果Tab.2 Numerical results of the exact and imaginary parts when α=0.5, β=0.5

部分数值模拟结果：

图1 当α=1, β=1时精确解和近似解迭代 1次， 5次， 50次虚部图Fig.1 Imaginary part of the 1, 5 and 50 iteration of exact and approximate solution when α=1, β=1

图2 当α=β=1时精确解与各级近似解虚部Fig.2 Imaginary part of exact and approximate solutions of all levels when α=β=1

图3 当β=1时，α对虚部的影响Fig.3 Influence of α on approximate solution when β=1

由表1发现迭代到5次后误差几乎已经消失了，而图1的数值结果表明，U5,U50已经和精确解靠得很近。在图2，图3中U5和精确解已经重合，因而该算法具有良好的实用性和精度。

4 总结

通过修正Laplace变换迭代法求解一类NLS方程，得到了方程的各级近似解，并进行了误差分析和数值模拟。研究结果表明，这一方法对于NLS类复偏微分方程近似解的处理规范有效。