基于双向门控循环单元神经网络的间歇过程最终产品质量预测

骆 楠， 祁佳康， 罗 娜

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）

间歇过程作为一种重要的生产方式，多用于生产低产量、高附加值的产品。然而，由于原材料成分的不确定性、产品品种的频繁改变及复杂的工艺过程，间歇过程的产品质量波动较大[1-2]。一方面，大多数间歇生产过程由于产品质量指标的检测缺乏在线传感器或难以在线测量，只能通过实验室化验分析得到分析值，难以满足质量指标实时在线控制的需要。另一方面，间歇过程的机理模型很难得到，因而基于数据的模型就成为了研究热点[3-4]。

与连续过程相比，间歇过程数据除变量和时间两个维度以外，还包括批次的维度。针对这种特殊性，Nomikos 等[5]提出了多向偏最小二乘法（MPLS），将作为自变量的三维数据按批次展开为二维数据，建立偏最小二乘模型，从而实现了产品质量预测。支持向量机方法较好地解决了小样本、非线性、高维数、局部极小等实际问题，具有很强的泛化能力，因而被用于复杂非线性间歇过程，特别是生化过程的质量预测问题[6-7]，并在青霉素发酵过程中验证了该算法的有效性。对于间歇过程产生的数据，简单的非线性特征可以使用传统的算法进行提取，但其批次间隐含的时序特征[8]仍难以提取。

循环神经网络(Recurrent Neural Network，RNN)通过将时序的概念引入到网络结构设计中，在时序数据分析中表现出更强的适应性，为提取时间序列特征提供了更好的解决方案。随着处理时间序列长度的增加，使用常规激活函数会使得网络训练期间容易产生梯度消失等问题，从而导致RNN 网络预测精度不足。而其变体，如长短期记忆(Long Short-Term Memory，LSTM)、门控循环单元(GRU)以及模型的双向操作等，通过添加一些阈值门弥补了RNN 的缺陷，这些方法已被广泛应用于多个序列学习问题中。在工业上，Wang 等[9]提出了深度异构GRU 模型的框架，用于刀具磨损预测；Yu 等[10]利用基于双向循环神经网络的自动编码器方法对涡轮风扇发动机进行了寿命预测；Wang 等[11]采用LSTM 对间歇过程中每个阶段的长时间序列进行特征提取，从而得到与质量相关的综合隐藏特征。来自于不同阶段的隐藏特征通过堆叠自动编码器进一步集成和压缩，进而实现了间歇过程的质量预测，但该建模方法只考虑批次内数据，并没有考虑原料的不确定性对不同批次产品质量的影响，因而对于某些复杂的间歇过程难以实现准确的质量预测。

在实际生产中，一方面原料存在一定的不确定性，如作为混合物的原料难以保证所有批次都完全一样；另一方面为防止产品出现不可挽回的质量损失，通常要求模型的预测值尽可能低于或者高于目标值，从而降低由于模型预测误差所带来的生产损失。针对以上问题，本文对双向门控循环单元(BiGRU)的损失函数进行了改进，并将其用于间歇过程质量指标的预测。双向循环神经网络可以整合前后批次数据时序信息，充分挖掘原料不确定性带来的批次间时序特征。改进的损失函数通过对不同的预测值施加不同的惩罚，使得预测值满足实际生产中的要求，提高算法的实用性。

1 基于BiGRU 的间歇过程最终产品质量预测

1.1 间歇过程的数据表示

间歇过程为多次重复生产[12]，与单纯的时序数据相比，其数据中还包含了间歇过程的批次，因而一般以三维数据 X(I×J×K)表示，矩阵 Y(I×1)表示最终产品质量变量，其中I 表示间歇过程的批次，J 表示过程变量的维数，K 表示每一次间歇过程的采样数，如图1 所示。

图 1 间歇过程中的数据Fig. 1 Data in batch processes

在实际生产过程中，常常存在外购原料产品质量不确定或自产原料生产过程不稳定而导致的原料供应波动频繁问题，造成模型输入变量的不确定，对采用传统算法进行系统建模与分析造成严重困扰[13]。然而这种不确定性最终在各批次生产过程变量中得以表现，即各种不确定性的隐藏信息能够通过图1 所示的三维数据间接得到。本文采用双向门控循环单元神经网络对序列数据进行特征提取，以期得到足以反映不确定性的隐藏特征，改善模型的预测精度。

1.2 循环神经网络

循环神经网络的优势在于处理时序数据，具体表现为网络中当前时刻的输出依赖于网络对之前信息的记忆，即隐藏层的输入不再是单纯的当前时刻输入层的输出，还包括前一时刻的隐藏层的输出。常见的循环神经网络的结构主要有3 种，包括两种多对多结构以及一种多对一结构，如图2 所示。

图 2 RNN 结构Fig. 2 RNN structure

图2 中多对多的结构有两种，第1 种要求输入序列与输出序列等长，因此该结构应用范围较窄；第2 种结构中输入、输出为不等长的序列，是一种Encoder-Decoder 结构，常用于机器翻译、语音识别等领域[14-15]。而多对一的结构则常用于处理序列分类或者回归问题，最终只需给定一个输出结果，因而本文选取多对一的循环神经网络结构，具体的网络预测结构如图3 所示。

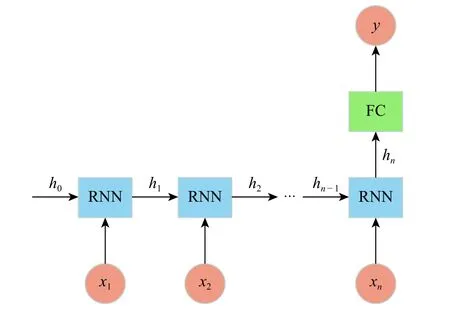
图 3 RNN 网络预测结构图Fig. 3 RNN network prediction structure diagram

对于给定序列 x =(x1, x2, ···, xn)，RNN 通过对输入空间和内部状态空间分别进行操作，计算出隐含层序列 h =(h0, h1, h2, ···, hn)，并由 RNN 的终端输出计算得到最终的预测值，如式(1)、式(2)所示。

其中：xt、ht分别为t 时刻的网络输入、网络输出；Whh为隐含层到隐含层的权重；Wxh为输入层到隐含层的权重；bh为隐藏层的偏置；fa为激活函数；g 为预测问题的仿射函数。

RNN 的单层网络结构以及基于BPTT（Back Propagation Through Time）的网络参数求解算法决定了RNN 在训练过程中会存在梯度消失或者梯度爆炸的情况，网络参数学习困难，很难学到长期的依赖[16]。

1.3 门控循环单元

由Hochreiter 等[17]提出的LSTM 神经网络是在RNN 的基础上发展而来，相对于RNN 的网络结构更为复杂，在RNN 的基础上增加了3 个门结构，即3 种不同的网络结构。每种网络结构的神经元数目是一致的，通过控制门的开关进而控制信息流的传递，在一定程度上缓解了RNN 存在的梯度消失或者梯度爆炸问题。LSTM 的结构单元如图4 所示。其中sigmoid、tanh 分别为神经网络的激活函数，具体公式如式(3)、式(4)所示。

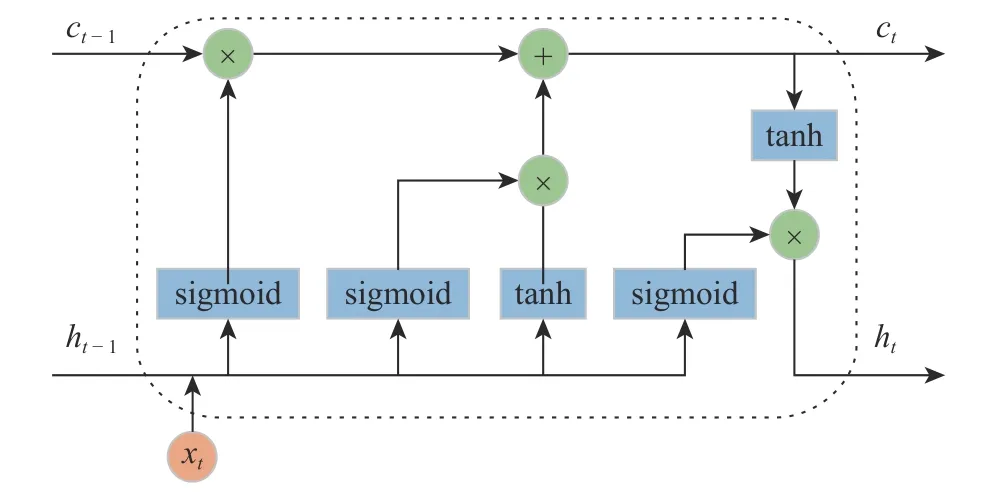
图 4 LSTM 单元结构图Fig. 4 Structure of LSTM

门控循环单元由Cho 等[15]于2014 年提出，并将其用于机器翻译领域。GRU 与LSTM 相仿，都是通过引入特殊的门结构来减少梯度弥散，使得误差得以长距离地传播，从而有了长期记忆的能力。不同的是，GRU 将LSTM 的门结构减少为更新门和重置门，模型更加简单，网络参数更少，收敛更快。GRU 的具体结构如图5 所示。其中GRU 中的更新门替换了LSTM 中的遗忘门和输出门，用于控制当前信息中哪些信息需要流入候选状态。更新门的具体公式如式(5)所示。

门控循环单元

重置门决定了前一时刻隐藏层单元输出ht-1对候选状态的影响。具体公式如式(7)所示：

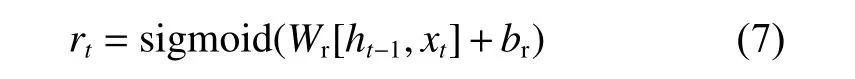
其中：Wr为重置门的权重参数；br为重置门的偏置。

最后GRU 的输出单元由上一时刻隐藏层输出、更新门状态以及当前候选状态共同决定，如式(8)所示：

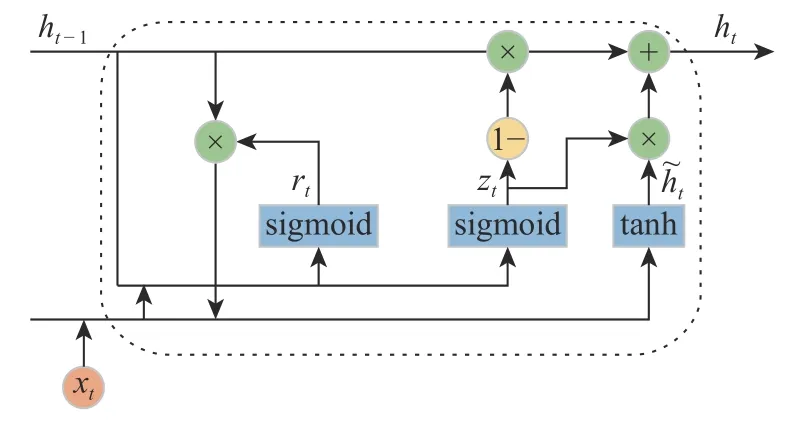
图 5 门控循环单元结构图Fig. 5 Structure of GRU

1.4 双向循环神经网络

Schuster 等[18]于1997 年提出了双向循环神经网络（BiRNN）。相较于普通的单向RNN 信息只能在正时间方向上进行传播，BiRNN 拥有两组隐藏层信息，一个是用于正时间方向上的输入序列，另一个是在负时间方向上的输入序列。因此BiRNN 可以更好地捕获时间序列中的信息，在语音识别、机器翻译、情感分类等方面得到广泛应用[19-20]。具体结构如图6 所示。

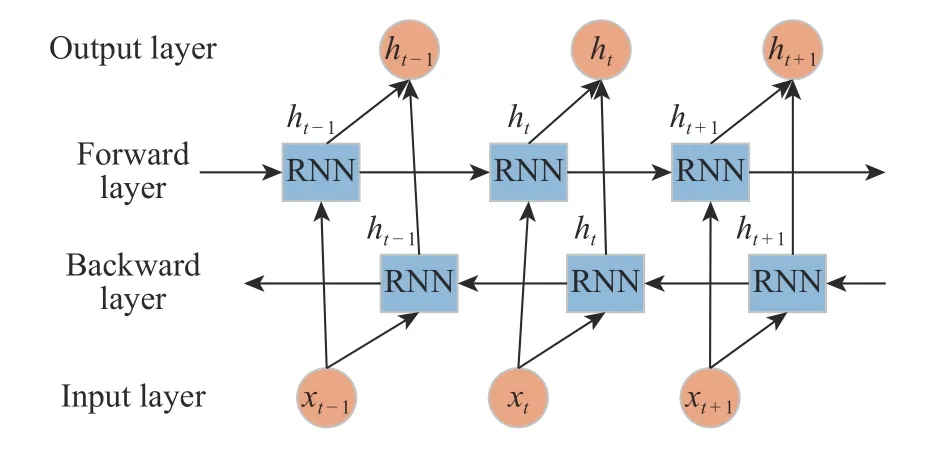
图 6 BiRNN 结构图Fig. 6 Structure of BiRNN

BiRNN 的输出由正向层的隐藏层输出与反向层的隐藏层输出构成，如式(9)所示：

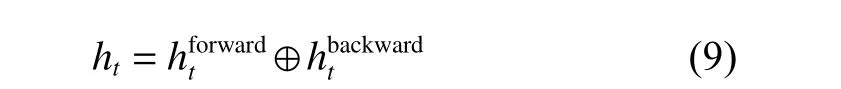
其中： ⊕ 为连接运算符； ht表示 t 时刻 BiRNN 的输出状态。

传统算法被广泛应用于批次内模型的建立，同时传统的批次间的模型无法充分挖掘到批次间的时序特征信息，而RNN 在时序数据建模中表现优秀。考虑到 RNN 存在长期依赖的问题，而 LSTM 和GRU 可以弥补此问题，同时GRU 相较于LSTM 网络参数少，便于模型的训练，因此本文采用BiGRU 作为预测模型的主要部分，从而可以提取到丰富的特征信息，提高模型的精度。

1.5 损失函数的改进

神经网络中的损失函数，又叫误差函数，用于刻画神经网络中输出值与真实值之间的误差程度，损失函数越小，模型的鲁棒性越好。神经网络的训练是经过前向传播计算损失函数值，并通过反向传播不断更新网络的权重和偏置，从而使损失函数不断减小至最低值。均方误差（Mean Square Error，MSE）是神经网络中最常见的损失函数之一，用于表征预测值与目标值之间误差平方的均值，如式(10)所示：

由于MSE 对预测值与目标值的差进行平方操作，仅仅考虑了预测值偏离真实值的程度，当预测值偏高于或者偏低于目标值同一程度时，MSE 给予相同惩罚。

虽然可以使用损失函数评估模型性能，并能提供优化的方向，但没有哪一种损失函数能满足所有预测需求。损失函数的选取依赖于选取的算法、参数数量、异常值、导数求取的难易和预测的置信度等若干方面，因此需要根据要处理的实际问题来确定相应的损失函数[21]。

在实际模型预测中，往往期望在满足预测精度的前提下，预测值尽可能低于或者高于目标值。例如Zhao 等[21]考虑到发动机的维护与更换的实际情况，在利用神经网络对发动机的寿命进行预测时指出，模型预测的原则是在预测值应该处于发动机即将报废时，即在保证模型预测精度的同时，预测值应该尽可能低于真实值。而在某些间歇过程中，为了保证效益的最大化，对于最终产品质量的预测有时也会要求预测值高于或者低于真实值，不同的产品要求不同，需要就具体问题而言。本文针对间歇过程最终质量预测的特点，提出了不对称损失函数（Asymmetric Loss Function，ALF），如式 (11)、式 (12)所示。

式中：ypredict,i为第 i 个样本的预测值；yactual,i为第 i 个样本的真实值；di为第i 个样本的预测值与真实值的差；a 和 b 均为自定义系数。当 a＞b 时，期望预测值大于真实值；当a＜b 时，期望预测值小于真实值。

为了更好地说明该损失函数的优点，选取a＞b 的情况，将其与MSE 进行对比。针对单一样本，两个损失函数的对比结果如图7 所示。

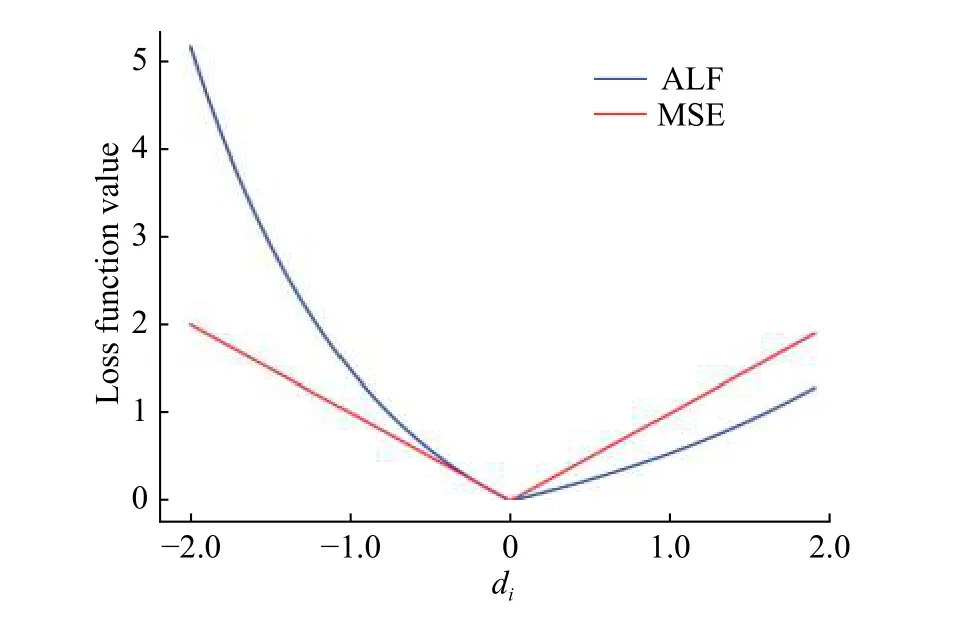
图 7 损失函数对比图Fig. 7 Comparison of loss functions

由图7 可看出，当预测值大于真实值时，ALF 相对于MSE 变化更为平缓，给予的惩罚较小；当预测值小于真实值时，ALF 相较于MSE 增长趋势明显加快，给予的惩罚较大。以ALF 作为神经网络的损失函数对网络进行训练，可以有效地调整惩罚值的大小，使预测值尽可能偏高于真实值，满足期望的预测原则。

2 实例分析

2.1 实验数据集

树脂生产是一个多阶段间歇过程，其生产过程主要包括缩聚和干燥脱水两个阶段，每个阶段都有特定的控制目标、不同的主导变量以及过程特性[22]。在缩聚阶段，首先将酚类、醛、催化剂依次加入反应釜中进行缩聚反应，一段时间后切换至干燥脱水阶段；在干燥脱水阶段，反应釜抽真空，在一定的真空度下树脂脱水，维持一定时间后，破真空取料，生产过程结束[23]。其中作为反应物的酚类本身为一种混合物，存放于中间罐中，随着时间的推移，里面的成分也随之缓慢发生变化，具体可通过色谱分析其组成，但一般情况下不分析，即使分析，也难以分析出所有物质。因而，原料成分的不确定性为准确预测过程最终产品的质量带来很大难度，同时这种不确定性伴随着时间的变化，即过程批次本身存在一定的时序性。本文以某类树脂的生产过程为研究对象，对树脂的软化点进行预测。

2.2 数据采集与处理

采集400 批生产过程中的过程变量数据，包括酚类和醛的流量以及反应釜的压力、温度和质量，实验室离线测得的树脂软化点作为预测变量。由于树脂的操作流程通常是固定的，根据生产过程中的操作条件获取不同操作阶段反应釜温度、质量和压力的起始值和终止值，将原有的不等长过程数据提取为各批次等长的过程数据，并根据原料的流量得到各批次反应物的质量。根据最大信息系数对过程数据和反应物质量进行特征选择，选择出与树脂软化点相关性最强的4 个变量，分别为醛的加入量、反应起始的温度值、反应终止的温度值以及真空度，得到模型的输入变量X400×4。为避免各变量的量纲对模型预测结果的影响，利用最大最小值法对样本进行归一化处理。

2.3 模型评价指标

选取均方根误差(RMSE)、R2来评估模型拟合结果的好坏。其中RMSE 体现模型预测值偏离真实值的平均程度，R2用来评估模型的可靠性。此外，为了更直观地表示改进损失函数后的优越性，采用可达率（Reachable Ratio，RR）来表征预测值高出真实值的个数。3 个指标的定义如式(13)～ 式(15)所示。

2.4 模型的建立

利用树脂生产过程数据，通过程序自循环寻优的方法进行模型参数设定，主要调节的参数包括时间窗口大小、网络结构和训练次数等。通过限定变量法，每次改变一个参数并监测RMSE 值，比较分析确定最优参数，为减小模型训练中随机性的影响，重复操作10 次取平均值。

由于BiGRU 神经网络需要输入时间序列数据，对400 个批次数据以滑动窗口为5 进行连续采样，将各滑动窗口的最后一个批次数据对应的质量指标作为模型预测值，得到396 个样本。为更好地挖掘数据中存在的不确定性，将其中前350 个样本为训练数据集，后46 个样本为测试数据集。最终本文的预测模型结构如图8 所示，设置BiGRU 神经网络的隐藏层神经元个数为80，采用Adam 优化器对网络参数进行训练，epoch 为 100，batch_size 为 20。

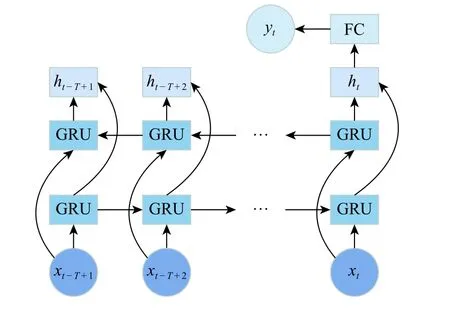
图 8 模型结构Fig. 8 Model structure

为了证明所提出的损失函数的优越性，分别选取MSE 和ALF 作为神经网络的损失函数，对模型进行训练。在树脂生产过程中，当树脂的软化点低于期望值时，可以通过补加醛提升树脂的软化点，而树脂的软化点高于期望值时，会导致该批次产品价值降低。为了保证生产效益，树脂软化点的预测原则与发动机寿命的预测原则恰恰相反，软化点模型预测的结果应该高于真实软化点值。针对树脂软化点预测模型，ALF 中参数 a、b 分别设为 1.7、0.8。

2.5 结果分析

为了说明本文模型在树脂质量预测中的有效性，将 MPLS[5]、SVR[6]、NN[24]、损失函数为 MSE 的GRU 模 型[9]（ GRU-MSE） 、 损 失 函 数 为 MSE 的BiGRU 模型（BiGRU-MSE）[18]与损失函数为 ALF 的BiGRU 模 型 （ BiGRU-ALF） 进 行 性 能 比 较 。 在SVR 中，利用网络搜索进行寻优，最终核函数选择高斯核函数，C 为 3.1，σ 为 0.1；在 NN 中，全连接神经网络层数设置为3，隐藏层使用sigmoid 激活函数，各层的神经元个数为{80，40，1}；GRU-MSE 则由 GRU 以及全连接层构成，神经元个数分别为70 和1，全连接层使用 sigmoid 激活函数；BiGRU-MSE 由 BiGRU 以及全连接层构成，神经元个数为65 和1，全连接层使用sigmoid 激活函数。图9 为6 个模型对43 个生产批次数据的预测结果对比图。

由图9 可以看出，MPLS 的预测效果最差，而SVR 与NN 的预测结果相似，部分批次预测结果偏差较大，都略差于GRU 模型。GRU 模型的预测效果比传统算法有了极大的提升，说明在对存在原料不确定性的间歇过程进行特征提取时，GRU 凭借着更强的记忆能力，挖掘到时序方面的特征，同时也说明间歇过程最终产品质量指标与原材料成分的变化有着密切关联。GRU 的拟合程度总体上较优，但是个别批次表现不够理想。而BiGRU 综合考虑了正向时序特征与反向时序特征，得到更为深层次的全局特征，预测结果较优于GRU。图10 为各GRU 预测结果的绝对误差对比分析图。

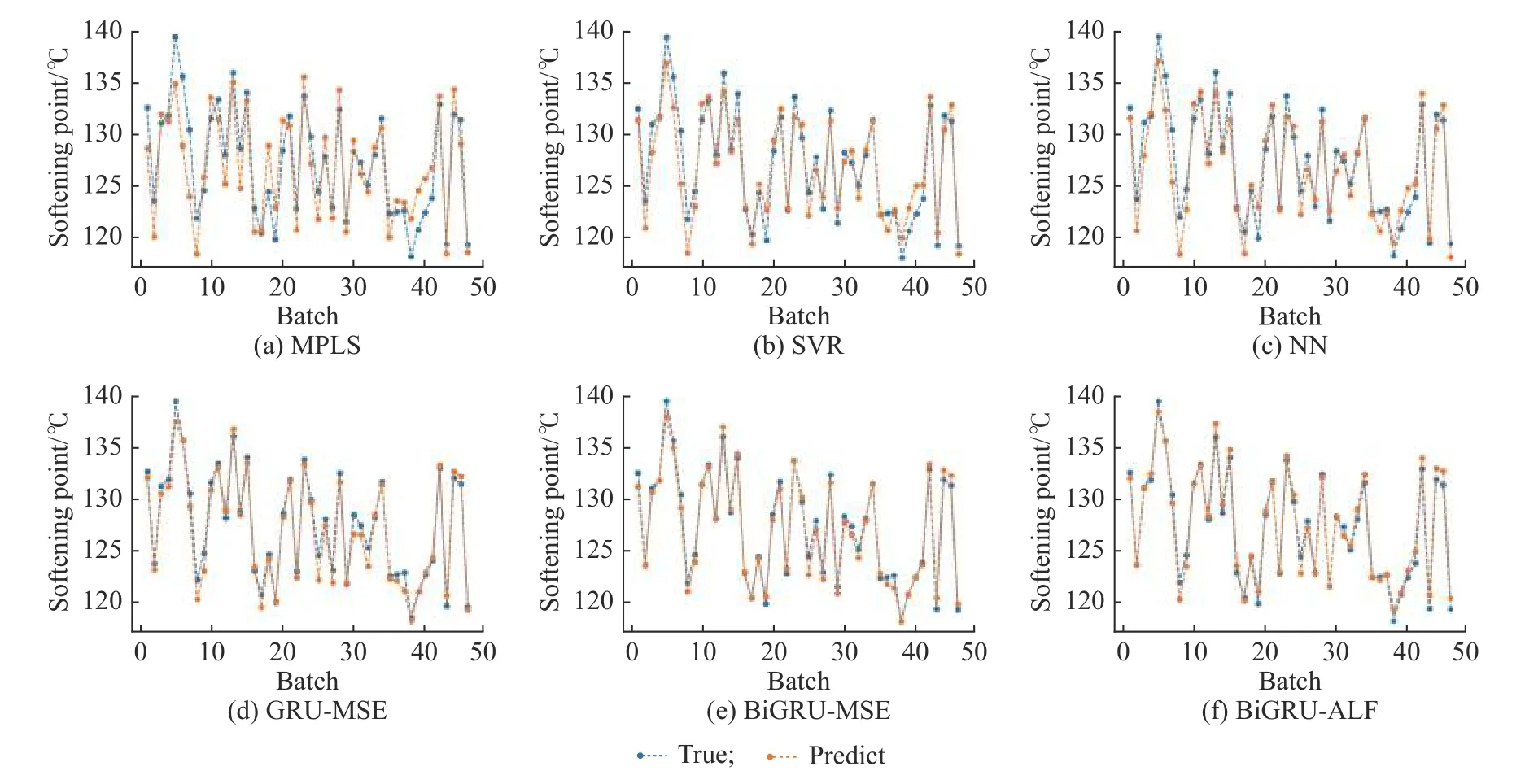
图 9 6 种算法的软化点预测结果Fig. 9 Softening point prediction results of six algorithms

图 10 3 种算法预测结果的绝对误差对比图Fig. 10 Absolute error comparison of three algorithm prediction results

从图 10 可看出，相较于 BiGRU-MSE，BiGRUALF 的绝对误差（真实值减去预测值）大部分在0 刻度线以上，即BiGRU-ALF 预测结果普遍有所提升，表明改进后的BiGRU-ALF 在满足预测精度、确保效益最大化方面的效果符合实际需要，进一步说明了改进后的算法具有更好的工业实用性。因为NN 与GRU 这类机器学习算法在预测结果上存在小范围的波动性，将20 次训练结果的平均值进行算法性能比较，用于更清晰地说明该网络结构的有效性。

表1 列出了针对测试样本计算出的评价指标结果，从表中可看出BiGRU-MSE 模型的预测精度相较于其他模型有了明显的提高，说明BiGRU 可以获得原料不确定性带给批次生产过程的更为准确的时序规律。虽然BiGRU-ALF 的预测精度低于BiGRUMSE，但是其可达率较高，同时BiGRU-ALF 的预测精度也略高于GRU-MSE 的预测结果，即BiGRUALF 模型能够在保证模型精度的情况下，更好地满足工业生产中关于最大化经济效益的要求，也表明改进后的双向门控循环单元神经网络更适合用于树脂软化点的预测。

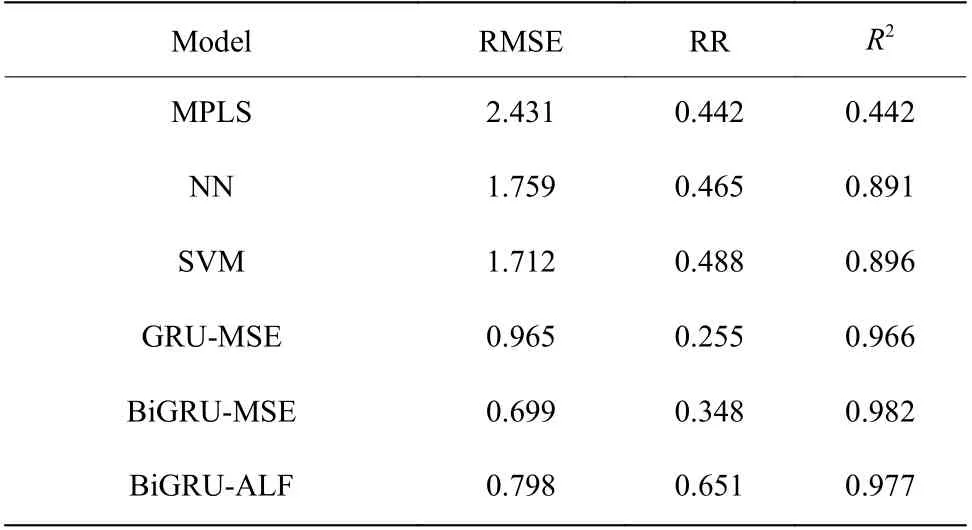
表 1 算法性能对比Table 1 Performance comparison of different algorithms

3 结 论

针对传统算法难以解决原料不确定下间歇过程的建模问题，本文提出了基于BiGRU 模型的间歇过程产品质量预测方法，并在某类树脂的软化点质量预测中进行了方法验证。与MPLS、NN、SVR 以及GRU 算法相比，基于BiGRU 模型的间歇过程产品质量预测方法获得了比传统算法更好的预测结果，验证了双向门控循环单元神经网络对工业间歇过程数据有着更好的预测能力。为了提高系统的容差率和预测结果的实用性，本文采用BiGRU-ALF 模型，通过对预测结果的不同偏差，给予不同的惩罚，使得预测结果拥有更大的安全裕度，为间歇过程的建模研究提供了新的思路，也对深度学习在间歇过程中的现场应用提供了一定的指导。