直升机发动机进气道外形曲面重建方法研究

钟德辉，曾建华，李 明，刘 飞

(1.中国直升机设计研究所，江西 景德镇 333001;2.中国人民解放军32380部队，北京 100072)

0 引言

逆向工程是将已有产品或实物模型转化为工程设计模型和概念模型，在此基础上对已有产品进行解剖、深化和再创造的过程[1]。当前，随着数字化测量技术的迅猛发展，逆向工程技术在航空航天、汽车工业、模具行业、艺术品仿制与破损修复等领域得到了广泛应用。如文献[2-4]论述了基于非接触式测量的汽车零部件、航空螺旋桨桨叶的模型重构，但其面对的对象特征较为简单，且未对建模方法进行系统的总结和研究，适用范围较窄。此外，针对逆向建模过程中经常遇到的点云数据拼接问题，相关研究报道较少。

随着直升机产业的快速发展，逆向工程技术在直升机型号设计、改进、改型等领域的作用越发凸显。本文针对直升机研制过程中的逆向建模需求，开展了多视角点云数据拼接及自由曲面拟合方法研究，成功构建了逆向数模，满足了型号研制需要。

1 数据获取与预处理

1.1 数据获取

点云数据获取是进气道逆向建模的首要环节，是进行数据处理、模型重构的基础。考虑到发动机进气道外形为较复杂的自由曲面，传统的接触式坐标测量法无法满足建模准确度要求，故采用非接触式测量法中的激光三角法来获取点云数据。该方法以空间交会原理为基础，基本原理如图1所示[5]。

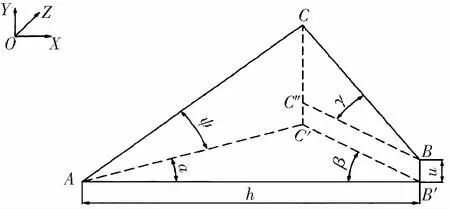
图1 激光三角法原理

图1中A、B分别为设备探头位置，C为被测点，B′、C′分别是B、C在A所在水平面的投影，C″为C在B所在水平面的投影。以A点为原点，AB′为X轴，过A点铅垂线向上为Z轴，定义右手坐标系OXYZ。设C点坐标为(X、Y、Z)，α、β、γ、ψ分别为C关于A、B两经纬仪的水平测角和俯仰测角。

假设AB′=h，BB′=u已知，且令

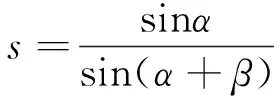
(1)

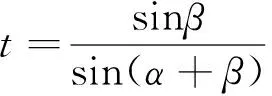
(2)

则

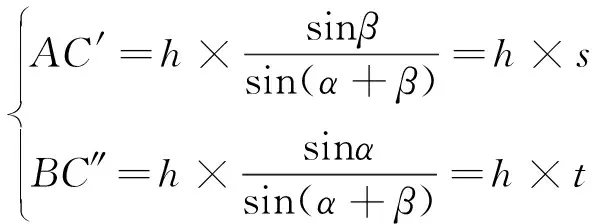
(3)

可推导出C点的坐标为

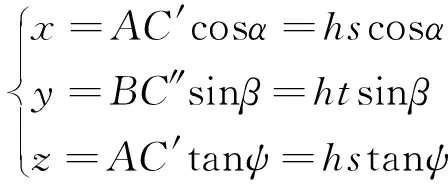
(4)

该方法具有精度较高，适应性强等特点，且能测量各种材质表面，无需进行测头补偿。采用该方法获取某型发动机进气道数模的点云数据如图2所示。

图2 进气道数模点云数据图

1.2 数据预处理

点云数据预处理是逆向建模过程中的重要环节，点云数据的质量直接影响到后期模型重建的质量。采用Geomagic软件平台对点云数据进行预处理，主要包括去除噪声点、补洞、光顺、简化等。

1)去除噪声点：扫描获取的点云中包括许多噪声点，如环境影响带入的噪声点、被测对象周边杂物等，可以结合通过切换视角、放大等操作选择噪声点做删除处理；

2)点云简化：一般原始点云数据量较大，处理速度较慢，可以根据实际需求精简点云，提高数据处理速度；

3)孔洞修补：由于被测对象表面质量及测量环境等因素的影响，局部点云数据缺失形成孔洞，这些孔洞直接影响后续曲面重建，必须对其进行填充，有时候直接填补孔洞的效果并不理想，可以把孔适当挖大，删除孔附近质量不好的点云数据后再填充；

4)光顺：通过采用最小二乘法、能量法和小波分析法来实现，主要用来删除钉状物，减少噪音等，使点云数据变得更平滑光顺。

具体经过预处理后的进气道木模点云数据如图3所示。

图3 经过预处理后的进气道木模点云数据图

2 点云拼接

2.1 拼接原理

当前应用最广泛的点云数据拼接方法有迭代最近点(ICP)算法及其改进算法。ICP算法是一个性能优越的精确拼接算法，但其运行速以及面向全局最优的收敛性却在很大程度上依赖于拼接数据的初始拼接位置[6]。本次需拼接的点云数据为发动机进气道的六块制造木模，各木模之间不存在包含关系，若直接采用ICP算法进行拼接，将导致ICP算法不能收敛，匹配结果不可靠。为此，本文提出一种点云粗拼接与迭代最近点(ICP)算法相结合的拼接方法：首先利用点特征匹配的方法完成点云数据的粗拼接，解决ICP算法对初始拼接位置的要求，再应用ICP算法实现点云数据的精确拼接。

2.2 多视角拼接

点云粗拼接过程实际上是根据在点云上选取的点特征分别建立局部坐标系，然后通过平移和旋转变换的方式将两个坐标系下的数据统一到一个坐标系下。这个拼接过程就是寻找平移和旋转矩阵。

对进气道点云数据进行粗拼接时，分别在相邻两块点云数据的交界处依次构建若干个(3个以上)点特征并一一对应起来，通过数据处理解出两个方位间的坐标变换关系，从而实现两块点云数据的粗拼接。

点云数据的精确拼接采用ICP算法实现。该方法为当前较为成熟的方法，如Geomagic软件中的“最佳拟合对齐”。

本次拼接对象为6块独立的点云数据(木模编号分别为③⑤⑦⑨)，视角较多。实际拼接时发现，若逐一进行拼接，由于拼接误差累计，第一块和最后一块无法拼接到一起，如图4。

图4 逐一拼接效果图

为减小拼接误差的影响，对6块点云数据进行分析，并通过多次拼接尝试，最终得到最优拼接方案：首先将点云数据平均分为三组进行两两拼接(③和⑤，⑦和，⑨和组合)，得到三块新的点云数据、、；然后将其中两块新点云数据、拼接，得到点云数据；最后将、拼接得到最终的拼接点云数据。优化拼接方案如图5所示。

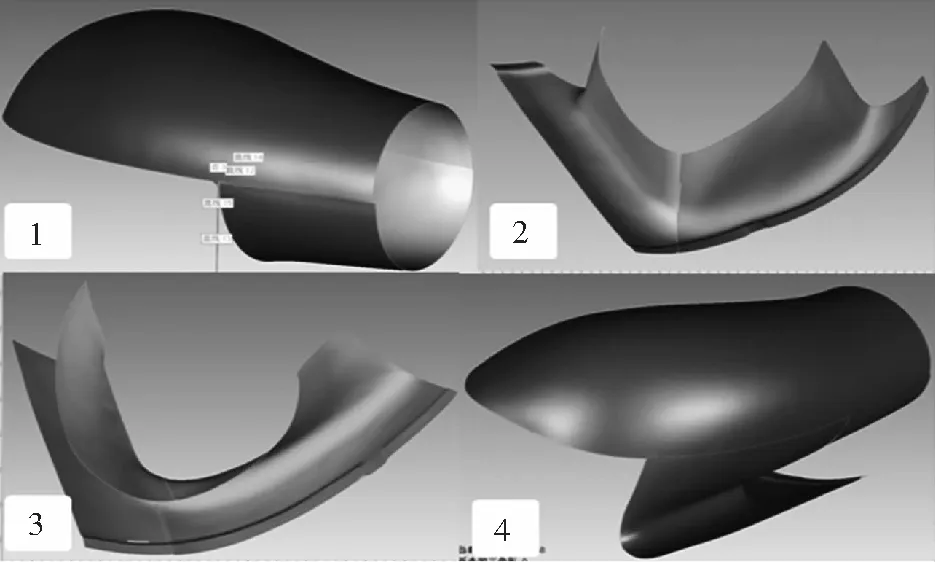
图5 优化拼接方案图

采取优化后的方案进行多块拼接，随着拼接对象逐步增大，拼接处的点云相互间的接触更为充分。可选取更多的特征点进行拼接，减小累积拼接误差，实现多视角拼接方案的优化。经分析,其拼接误差控制在0.25mm内，满足设计要求。优化后的点云拼接如图6所示。

图6 优化后的点云拼接图

3 曲面重建

3.1 区域划分

由于进气道型面由复杂的自由曲面构成，整体完成曲面拟合无法实现，故必须根据点云的特征将其划分成不同的区域，对每个区域分别进行曲面拟合，然后采用曲面间的过渡方法将各区域的曲面片拼接起来。

对进气道点云数据进行曲率分析，根据其曲率变化情况将其划分为三个区域。具体的点云区域划分如图7所示。

图7 点云区域划分图

3.2 曲面拟合

进行曲面拟合前，对划分的区域选取特征截面，建立特征线并对特征曲线进行光顺处理，最后进行曲面拟合。曲面拟合是逆向建模过程中最为关键的环节。针对进气道由自由曲面构成且对曲面精度和光顺度要求较高的特点，采用NURBS方法来进行曲面拟合。NURBS曲面的数学模型为：

有理分式形式：

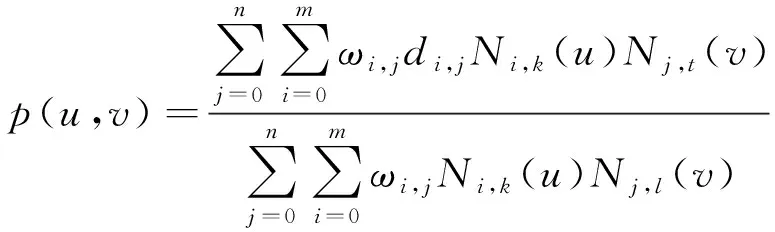
(1)

有理基函数形式：

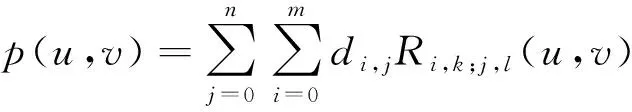
(2)

其中，

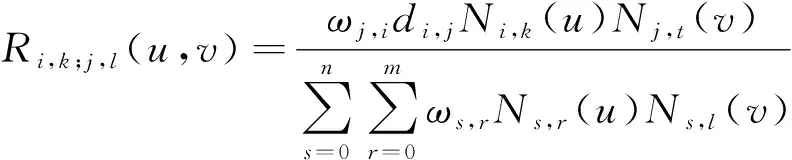
(3)

式中：di,j为控制顶点，呈拓扑矩阵，形成一个控制网络，i=0，1，…m，j=0，1…n，ωi,j为与顶点di,j联系的权因子，规定四角顶点处用正权因子，即ω0，0、ω0，n、ωm，n>0，其余ωi,j≥0，且顺序k×1个权因子不能同时为0；Ni,k(u)，Nj,l(v)分别为u向k次和v向l次规范B样条基。

NURBS方法具有良好的整体光滑曲面拟合能力和强大的局部调控特性，能够精确地表示自由曲面。利用该方法拟合得到进气道曲面拟合如图8所示。

图8 曲面拟合图

3.3 拟合误差分析

拟合误差分析的目的主要是检验曲面的拟合精度，若误差不满足设计精度要求，则需要调整曲面拟合方案，重新对相应曲面进行拟合，直到误差满足设计精度要求。

将拟合好的进气道曲面与原始点云数据进行分析，得到偏差结果为：最大偏差为0.25mm，最小偏差为-0.4mm，满足设计要求的曲面与点云重合度不大于0.5mm的精度要求。具体误差分析如图9所示。

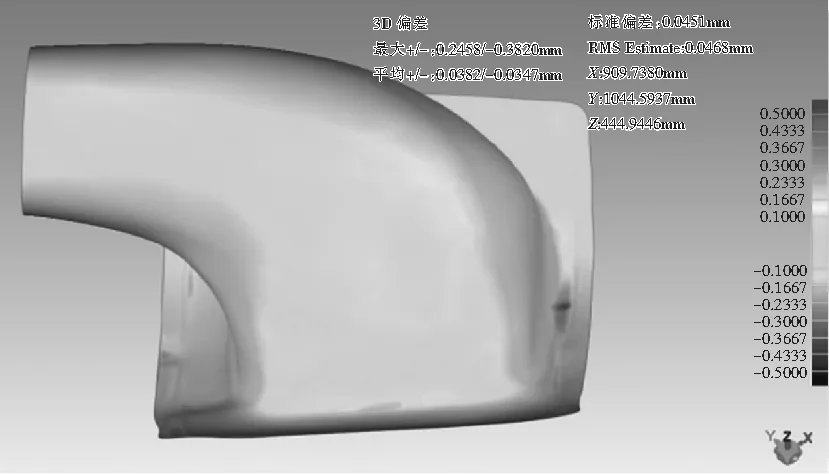
图9 误差分析图

4 结束语

本文以某型直升机发动机逆向建摸为例，提出了一套针对直升机复杂零部件高质量数模重建的方法。通过采用激光三角法高效获取外形点云数据，运用Geomagic软件平台完成了点云的预处理；提出了一种粗拼接与迭代最近点(ICP)算法相结合的点云拼接方法，同时在拼接过程中综合考虑了拼接累积误差的影响，通过多次优化拼接方案最终获得了较好的拼接效果；根据点云特点采用按曲率分块，并使用NURBS方法进行曲面拟合，最终实现了某型直升机进气道的逆向建模。该研究方法已在多个型号测绘任务中得到成功应用和验证，提高了设计效率。