基于多孔介质模型的某型无人直升机散热器仿真分析

严 雄

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

散热器是轻小型直升机发动机冷却系统中必不可少的一部分，其作用是将发动机水套内的冷却液通过散热器二次热交换，使热量在外界强制气流的作用下被空气带走，将发动机高温零件的温度保持在合理的范围内。若温度过高则会导致活塞卡死、零件破裂损坏、积碳、功率降低等问题，影响发动机的经济性甚至发生爆炸；若冷却过度则会导致燃料和功率消耗增加，硫化物与水蒸气凝结为亚硫酸溶液腐蚀零件等问题。故散热器性能的好坏直接影响着发动机性能。随着直升机对其机载设备的尺寸和重量要求都越来越严苛，散热器结构的进一步的优化和完善就显得很重要。

将多孔介质模型应用于模拟换热器中流体的流动和传热问题始于20世纪70年代，Patankar和Spalding首先提出了该方法[1]。之后，Karayannis等采用此方法模拟了换热器中的流动[2,3]，Prithiviraj和Andrews模拟了三维换热器中的流动[4]。国内，常柱宇采用多孔介质模型中的多孔阶跃面来模拟航空滑油滤网的阻力特性[5]，并详细介绍了多孔介质模型三个参数(黏性阻力系数、惯性阻力系数和厚度)的确定方法。朱冬生等人介绍了如何利用Fluent软件中的多孔介质模型，对板翅式燃气热水器换热器芯体内流体的流动与传热进行三维仿真计算[6]。理论基础、应用领域以及相应仿真验证的结果表明，采用多孔介质模型代替热交换器进行仿真计算具有可行性和有效性。

某直升机发动机冷却系统采用管带式散热器，其芯体结构复杂，空气侧布置有多层具有复杂传热面的百叶窗翅片。在进行仿真计算时，倘若直接对热交换器实体进行建模和仿真计算，计算区域离散(网格生成)将十分困难，耗用计算机资源将很大。因此，为了合理简化并有效实施仿真计算，本文确定应用多孔介质模型来替代真实的散热器芯体，对空气流量、液体流量等影响散热性能的因素进行分析和评估，为今后散热器优化提供方向参考。

1 模型建立

1.1 多孔介质模型概述

基于多孔介质模型的数值仿真方法是将流体、固体划入同一个控制体，通过对守恒方程及差分方法的修改来表现固体的影响，就是用体积穿透率即流体体积与整个控制体体积的比值表示固体构件对控制体内流体体积的影响，用表面穿透率即流体表面与控制体表面的比值来表示固体构件对控制体表面作用力的影响。

多孔介质模型适用的范围非常广泛，包括填充床，过滤纸，多孔板，流量分配器以及管束系统等。在参数设置过程中，多孔介质模型由黏性阻力系数、惯性阻力系数和厚度三个参数来确定。在Fluent中，多孔介质可以被应用于网格区域或者面区域。本质上，多孔介质模型就是在多孔区域设置了一个以试验结果和经验假设为主的流动阻力，即在动量方程上叠加了一个动量源项，所以，多孔介质可以大大简化模型的复杂程度，在显著缩减计算量的同时，保证了仿真计算结果的稳定性和准确性。

1.2 物理模型

本文研究对象为直升机管带式散热器，散热器芯体结构如图1所示。其中：G为扁管外侧宽度，G=2mm；扁管壁厚0.4mm；H为散热带波高，H=7.5mm；W为散热带宽度，W=32mm；B为散热带波距，B=2.5mm；散热带壁厚0.1mm，形式为直翅式。散热器芯体由45排扁管和46排散热带单排排列组成，芯体长、宽、高分别为570mm、32mm和435mm。扁管与散热带材料均为铝合金，牌号3003，相邻依次排列。

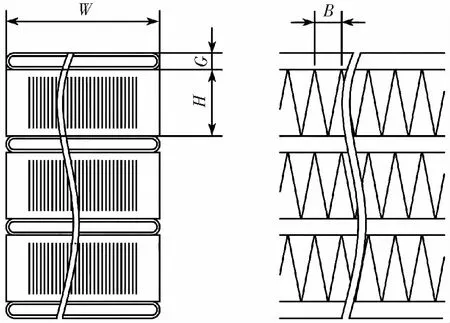
图1 管带式散热器芯体结构示意图

1.3 基本假设

根据管带式散热器的实际情况进行一定的假设以简化运算量，即：

1)流体为定常流动；

2)散热器两侧流动过程无相变；

3)空气的密度、黏度和导热系数等物理参数仅与温度相关；

4)忽略散热器与大气间的热辐射；

5)管带式散热器中带百叶窗翅片的波浪形散热带结构简化为多孔介质的长方体且无化学反应存在，其具体参数参考了相关文献并通过相关计算得到；

6)散热器水管壁简化成相应厚度的双侧壁面以减少固体网格数量。

1.4 数学模型建立

1.4.1 控制方程

多孔介质的控制方程与标准控制方程有所区别，但同样满足连续性方程、动量方程以及能量方程，分别介绍如下:

1)连续性方程—多孔介质的连续性方程与标准的连续性方程一样，可表示为:

2)动量方程—多孔介质的动量方程是在标准的动量方程的基础上附加动量源项而得到的:

(2)

其中源项由两部分组成，一部分是粘性损失项，另一个是内部损失项:

(3)

式中，Si—i向动量源项；D、C—粘性和惯性阻力系数矩阵；μ—流体粘度；ρ—流体密度；vjj—向流体速度。

源项直接导致多孔介质内压力梯度分布的改变。因此，压降与速度大小是呈一定比例关系的。

对于简单的均匀多孔介质:

(4)

式中，α—渗透性；C2—内部阻力因子。常数C2可以看成是沿着流动方向每一单位长度的损失系数。

3)能量方程—对于多孔介质流动，FLUENT 仍然解标准能量输运方程，只是修改了传导流量和过度项。在多孔介质中，传导流量使用有效传导系数，过渡项包括了介质固体区域的热惯量:

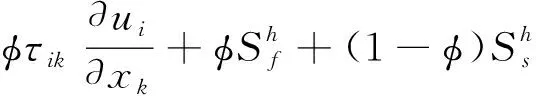
(5)

式中，hf—流体的焓；hs—固体介质的焓；Φ—介质的多孔性；keff—介质的有效传导系数。

1.4.2 边界条件及参数设置

经过简化后，利用Catia软件进行几何建模，获得的模型如图2所示。然后运用ICEMCFD软件进行网格划分，利用Fluent软件进行仿真求解，采用有限体积法将非线性偏微分方程转变为网格单元上的线性代数方程，然后通过求解线性方程组得出流场的解。采用基于压力的求解器进行控制方程的求解，Simple法耦合压力-速度，采用RNGκ-ε模型进行仿真。

图2 散热器模型

对于本文所仿真的对象，共有三类边界条件，分别为入口边界条件，出口边界条件，壁面边界条件。

1) 入口边界条件：本文模型入口边界设定为速度边界条件；

2) 出口边界条件：本文模型出口边界设定为压力出口边界条件，均为默认值；

3) 壁面边界条件：本文模型除耦合壁面外，其余壁面均设为绝热壁面边界。

2 计算结果分析

2.1 风量和冷却液流量的影响

由于该散热器在机上使用时是与风扇配套使用的，风扇为散热器提供冷却空气，因而风扇与散热器的良好匹配对散热性能的发挥有很大的影响。同样的原理，冷却液的流量也会对散热性能造成影响。本节通过改变风量和冷却液流量参数仿真计算，来分析其对散热器性能的影响。计算结果如表1所示(风扇性能参数取自同一厂家产品)。

表1 不同风量以及流量的散热器仿真结果

从表1可以看出，相同风量下，液体侧流量的变化对散热性能的影响较小，通过提升泵的性能来换取散热量的增加效率较低；相比较而言，风量对散热性能影响较为明显，但随着大风量风扇的使用，用电功率以及风扇的质量均会提高，这是需要综合考量的。并且如图3所示，风扇的选用需要根据散热器和风扇的结构及性能特性来匹配，两者组合工作时，需要保证散热器在额定流量条件下的流阻与风扇在额定流量下的压升指标相当以及非额定流量点流阻与压升的匹配，以满足散热器对空气流量的需求，最终保证所需散热功率。

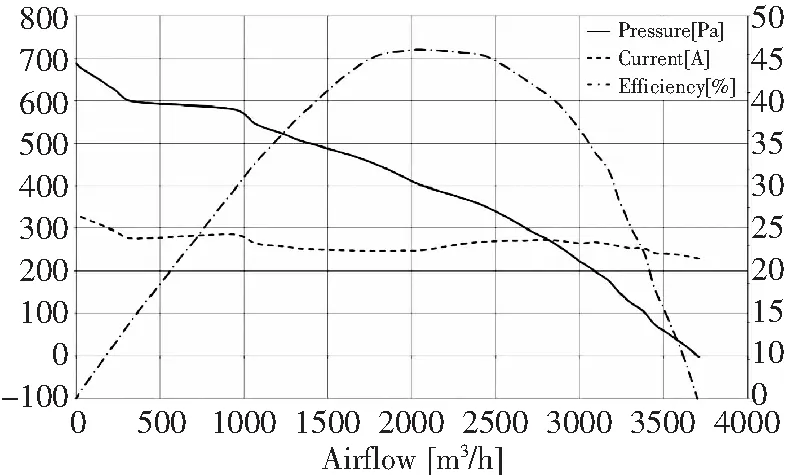
图3 风扇性能曲线

2.2 散热器芯体厚度的影响

本节对原散热器结构进行一定的改变，将散热器芯体厚度减小至27mm，但是迎风面长、宽不变，进行仿真计算，并将其与32mm厚度芯体的计算数据进行比较，如表2所示。

从表2可以看出，虽然27mm芯体相对32mm芯体而言，通过减小芯体厚度使芯体减重约20%，但是散热性能损失只有12%，液体边流阻也进一步降低。故综合考虑，在机载设备散热量富裕较多时，可以通过减小散热器芯体厚度，以较小的性能损失达到较好减重效果。

表2 不同芯体厚度的散热器仿真结果

3 结论

本文以管带式直升机散热器为研究对象，对散热器芯体进行了仿真计算。结果表明：

1)在其他条件不变的情况下，仅仅改变液体侧流量对散热性能影响十分有限；

2)通过增大空气侧流量，可以明显提升散热性能，但是随之而来的是用电量的提升，建议在机上用电相对富裕的情况下采用该方案；

3)通过减小散热器芯体厚度，可以在牺牲少量的散热性能的情况下减去较多重量。