汽车转向系统力矩波动优化及仿真分析

张 吉

（中国第一汽车集团有限公司研发总院，吉林 长春 130011）

1 前言

汽车转向系统因转向轴线不在同一条直线上，故存在不等速传动的特性，当波动量超过一定数值时（一般单侧不超过5%），驾驶员便会感到方向盘“时轻时重”的不舒适感。转向硬点优化就是为了减小力矩波动对驾驶员手感的影响。

整车制造厂都有各自转向力矩波动的优化方法[1][2][3]。将双十字轴简化为单十字轴万向节采用“等效夹角”的优化方法，经分析其存在计算误差；而基于Adams和Catia的优化方法，因建模和处理过程复杂，工作效率较低。本文基于Catia模型分析，通过实例阐述“等效夹角”方法存在的问题，并创建了满足多工况下转向力矩波动计算程序，经检验计算结果准确、可靠、高效。

2 转向力矩波动理论

单十字轴万向节传递关系如下[1]：

其中：φ1、φ2分别为输入轴和输出轴转角，β1为输入轴与输出轴夹角，ω1、T1、ω2、T2分别为输入轴和输出轴的转速和转矩。由式（2），ω2/ω1周期为π，即输入轴旋转一周，力矩波动出现两次。

空间双十字轴万向节传动如图 1，中间轴与输入轴、输出轴夹角分别为β1、β2，中间轴与输入轴、输出轴所成平面分别为P1、P2，两平面夹角为θ，输入轴、中间轴和输出轴的角速度、转角和转矩分别为ω1、θ1、T1、ω2、θ2、T2、ω3、θ3、T3，沿中间轴轴线自上而下（即M向）上、下两节叉所在平面沿顺时针方向的夹角定义为中间轴相位角α，取值范围 α∈ [0,180°]。

与（2）式同理，中间轴与输出轴的传递关系：

由式（2）和（3）得双十字轴万向节传递关系：

输出轴相对输入轴的力矩波动K（双侧）：

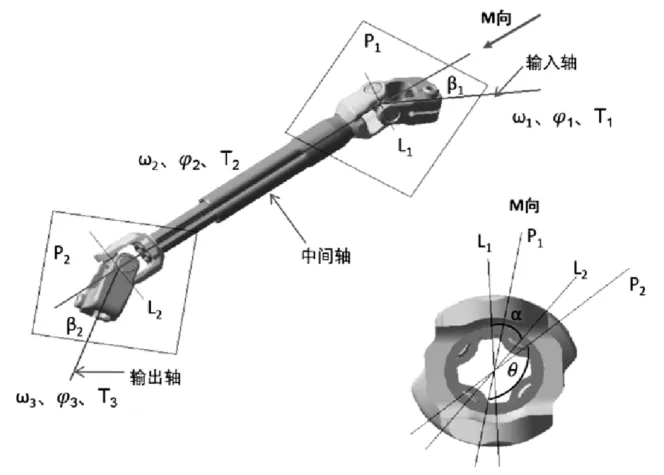
图1 空间双十字轴万向节传动示意图

有文献提出双十字轴万向节可简化为单十字轴万向节传动，其等效夹角βe按（7）式确定[1][4]：

由（7）式可知，当 α+θ=0、90°和 180°时，等效夹角最小值为，此时力矩波动最小。因相位角α∈ [0,180°]，而平面夹角θ一般不可能为0，故 α+θ 取值90°和180°均可满足要求，即当θ确定后会有两个最优相位角均满足最小力矩波动要求，力矩波动值按（8）式计算[1][4]：

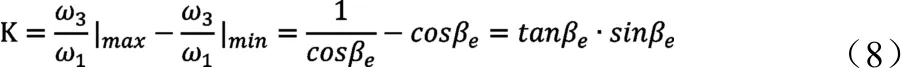
下面将通过 Catia模型进一步分析最优相位角取值及力矩波动值计算问题。

3 空间建模分析

表1为某车型转向系统硬点，如图2建立Catia分析模型，得：AB与BC夹角为30.042°，BC与CD夹角为32.017°，通过向量计算得平面P1和P2夹角θ为151.796°。为了进一步验证α+θ=90°和180°是否都可满足力矩波动量最小，分别取 α1=90°-151.796°=-61.796°，因 α∈ [0,180°]，故 α1=-61.796°+180°=118.204°，取 α2=180°-151.796°=28.204°。

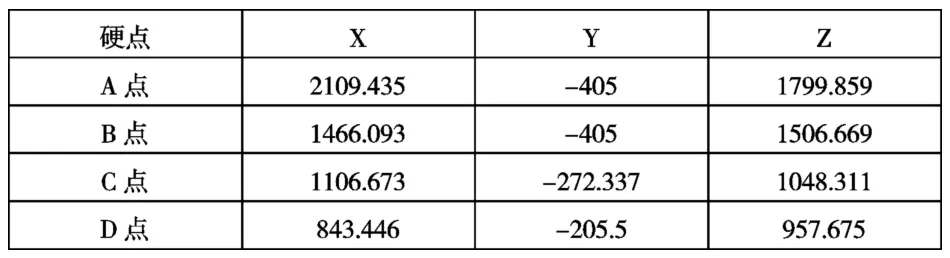
表1 某车型转向系统硬点

图2 转向系统Catia分析模型

为了分析不同相位角对力矩波动的影响，增加 α=60°、90°、150°和180°的情况，分析结果如图3。从曲线可以看出：①当α=28.204°时，转向力矩波动最小；②当α=118.204°时，转向力矩波动最大；③相位角α在[0,180°]内有且仅有唯一值保证力矩波动最小。

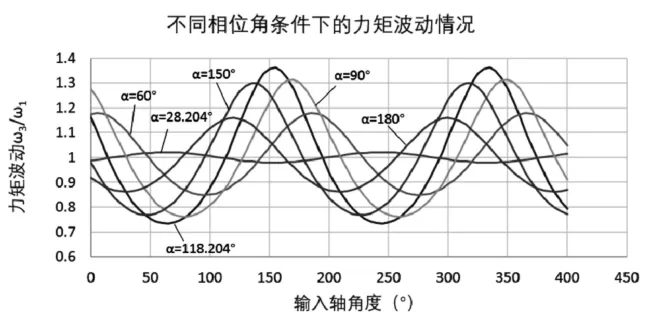
图3 不同相位角力矩波动分析结果

以上分析得知：当中间轴相位角α与两平面夹角θ之和为 180°时，转向力矩波动最小。按“等效夹角”方法，取α+θ=180°，得βe=11.072°，计算力矩波动值为 1.88%，而在同样条件下模型分析结果为 2.07%。当转向柱分别处于角度调节极限位置时（伸缩调节对力矩波动无影响），分别采用两种方法对力矩波动进行分析，结果如表 2，可以看出基于该车型力矩波动结果存在最大0.47%的偏差。

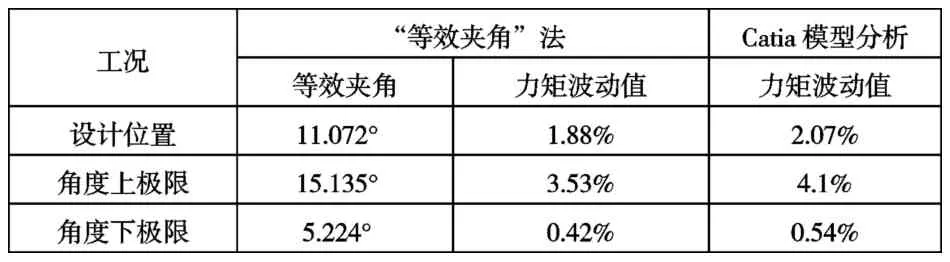
表2 “等效夹角”方法和模型分析结果对比

综上，“等效夹角”方法存在最优相位角取值不合理和力矩波动计算误差问题，在实际工作中不建议采用。

4 GUI编程与验证

为减少设计工作量，创建了面向用户的GUI程序，如图4。通过输入转向硬点参数，可得最优相位角，并基于任意相位角取值计算力矩波动值。

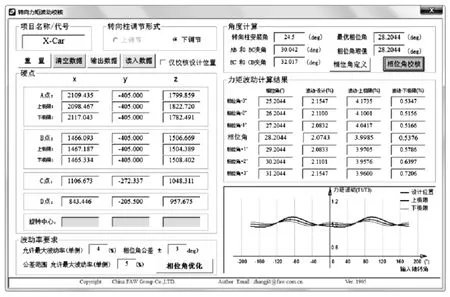
图4 GUI程序计算分析界面

图4为上述车型案例采用GUI程序计算的结果，最优相位角取值和力矩波动值与模型分析结果一致，其角度调节极限位置力矩波动校核结果与Catia模型分析结果（图5）一致。

对于平台化车型设计和设计方案反复优化时，可快速、准确完成计算，且该程序已经过多款现生产车型验证，实测结果与计算结果一致。

图5 不同角度调节位置力矩波动计算结果

5 总结

通过对汽车空间双十字轴万向节传动进行分析，并基于转向系统 Catia计算模型，指出采用“等效夹角”优化方法导致最优相位角不唯一和力矩波动计算误差大的问题，通过创建 GUI程序对最优相位角和任意相位角条件下的力矩波动进行计算，满足不同调节形式、调节位置及考虑相位角公差情况下的力矩波动校核。