基于MATLAB的轮胎侧偏刚度对汽车瞬态响应影响研究

吴云兵，胥峰，李兵，熊乐，张鹏飞，应宇汀

（中汽研汽车检验中心（宁波）有限公司，浙江 宁波 315336）

前言

汽车的操纵稳定性是指在驾驶员不感到过分行、疲劳的条件下，汽车能遵循驾驶员通过转向系及转向车轮给定的方向行驶，且当遭遇外界干扰时，汽车能抵抗干扰而保持稳定行驶的能力[1]。汽车瞬态响应特性是指瞬态状况下的运动响应，一般分为时域响应特性和频率响应特性。时域响应特性一般是基于角阶跃输入下瞬态响应，频率响应特性可以用横摆角速度的增益和相位角表示。

轮胎受力状况、运动状态以及与路面间的相互作用复杂性极大增加了轮胎力学特性研究的难度[2]。而轮胎的侧偏刚度又是轮胎的重要力学参数之一，对整车操纵稳定性有重要影响。因此，研究不同轮胎侧偏刚度对汽车瞬态响应的影响，对提高整车操纵稳定性有着重要意义。

本文通过建立线性二自由度汽车模型的横摆角速度传递函数，并利用 MATLAB编写角阶跃输入瞬态响应试验仿真程序，研究了不同轮胎侧偏刚度对汽车前轮角阶跃输入瞬态响应的影响。

1 轮胎的侧偏特性

轮胎的侧偏特性是轮胎力学特性的重要组成。侧偏特性主要是指侧偏力、回正力矩与侧偏角之间的关系，它是研究汽车操纵稳定性的基础。

轮胎坐标系与地面反力的关系如图1所示。垂直于车轮旋转轴线的轮胎中分平面称为车轮平面。坐标系的原点O为车轮平面和地平面的交线同旋转轴线在地面上投影的交点。车轮平面与地平面的交线为X轴，规定向前为正。Z轴与地平面垂直，规定指向上方为正。Y轴在地平面上，规定面向车轮前进方向时指向左方为正。

图1 轮胎的坐标系与地面反力

由于汽车行驶过程中常受到倾斜路面、离心力及侧风等因素的影响，当侧向力FY未到达附着极限的时候，车轮前进方向偏离车轮平面，上述便是轮胎的侧偏现象，侧偏角α即为车辆前进方向与车轮平面的夹角。试验结果显示，当侧偏角不超过 5°时，侧偏力FY与侧偏角α为线性关系。汽车正常行驶时，侧向加速度小于 0.4g，侧偏角不大于 4°～5°，便可将侧偏力FY与侧偏角α的关系当做线性关系，即：

式中：k为轮胎侧偏刚度。

2 整车二自由度动力学模型

为便于掌握操纵稳定性的基本特性，通常将车辆简化成一个由前后两个有侧向弹性的轮胎支撑于地面、且只具有侧向及横摆运动的二自由度汽车模型。

图2 二自由度汽车模型

当车辆侧向加速度值限制在0.4g范围内时，轮胎侧偏特性呈现线性关系。在车辆坐标系下，根据二自由度汽车沿y轴方向受力及绕质心的力矩情况，得到线性二自由度汽车运动微分方程为：

式中：k1、k2分别为前轮和后轮的侧偏刚度；a、b分别为汽车质心至前、后轴的距离；β为质心的侧偏角，且β=u/v；u、v；分别为质心速度V在车辆坐标系x、y轴上的速度分量，即纵向车速和侧向车速；ωr为汽车横摆角速度；δ为前轮转角；m为汽车质量；IZ为汽车转动惯量。

由式（2）可得：

对式（3）求导可得：

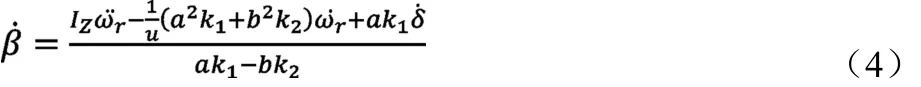
将式（4）代入式（2）得：

式（5）写成以ωr为变量的形式，即：

式（6）是单自由度一般强迫振动微分方程式，通常写成：

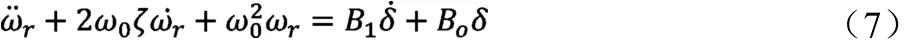
当给定前轮的输入为转角盘角阶跃输入，其数学表达式为：

当t＞0时，式（8）进一步简化为：

3 动力学模型的解析

微分方程（9）为二阶常系数非齐次，显然它的通解为它的对应的齐次微分方程的通解与特解之和。其特解为：

当K=0时，此时车速与横摆角速度与成比例关系，该状态称为中性转向（见图3）。

当K＞0时，较中性转向时偏低，车速与其不再呈现比例关系，此时的横摆角速度增益曲线低于中性转向，当汽车具备这种特性时便称作不足转向。当K值增大时，横摆角速度增益的曲线逐渐降低，不足转向量增加。车速达到的时候，横摆角速度增益的数值达到最大。uch称为特征车速，对汽车不足转向有着重要影响。

当K＜0时，较中性转向时偏高，此时的横摆角速度增益曲线高于中性转向，当汽车具备这种特性时便称作过多转向。当K值增大时（即K值的绝对值增大），带来更大的过多转向。车速达到的时候，车辆转向灵敏度值趋近无穷大，ucr被称作临界车速，对车辆过多转向量有着重要影响。临界车速减小时，带来更大的过多转向。

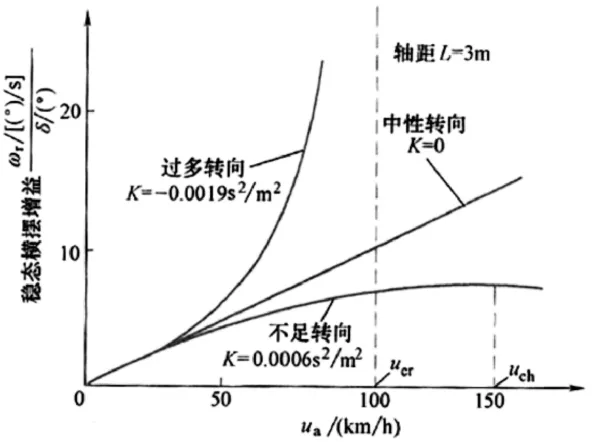
图3 横摆角速度增益曲线

式（10）对应的齐次方程为：

其通解可由如下的特征方程求得：

根据ζ的数据，特征方程的根为：

齐次方程的通解为：

上式中，积分常数 C、Φ、C1、C2、C3、C4的值需依照车辆的初始条件来计算。

当ζ＞1时，横摆角速度ωr(t)为持续增长的，为大阻尼。当时间持续推进时，ωr逐步接近稳态横摆角速度ωr0；一旦车辆速度超过其临界车速ucr，ωr便趋于发散，接近无穷大，该状态下车辆失稳。

当ζ=1时，横摆角速度ωr(t)曲线也是持续增长的且趋近ωr0，称作临界阻尼。

当ζ＜1时，横摆角速度ωr(t)是为减幅正弦曲线，且最终收敛于值ωr0，其瞬态响应为小阻尼。现代生产的汽车的瞬态响应通常为小阻尼，因此本论文只探讨前轮在转向盘角阶跃输入下，ζ＜1时状态下ωr(t)的变化规律，研究影响ωr(t)的结构参数。当ζ＜1时，其横摆角速度为：

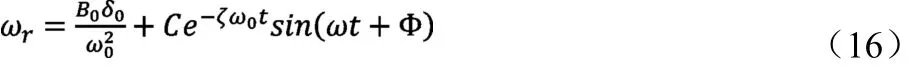
或

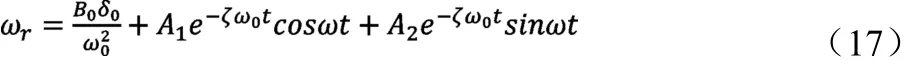
下面确定积分常数C、A1、A2。

车辆的起始运动条件是：当t=0，ωr=0，v=0，δ=δ0。根据运动方程式（2）能够得到t=0的时候，

由于t=0时，ωr=0，求得式（17）中的一个积分常数为：

由于t=0时，，可求得另外一个积分常数为：

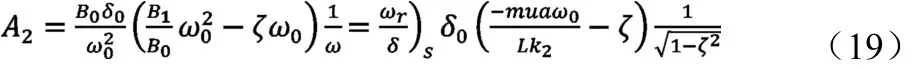
而

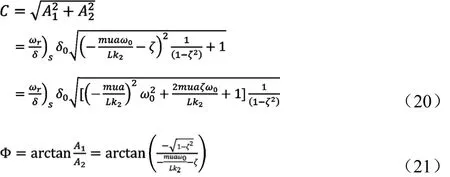
因此

图4 转向盘角阶跃输入下的汽车瞬态响应

式（22）便是当车辆前轮给定转向盘角阶跃输入装填下的横摆角速度瞬态响应。根据车辆的初始条件能够德奥，当t=0，ωr=0。由式（22）可知，t=∞时，也就是横摆角速度ωr(t)最终趋近稳态横摆角速度ωr0。随着t在0与∞之间变化，ωr(t)为一条正弦曲线，且是逐渐衰减的（见图4）。很明显地，当阻尼比增加，衰减速度加快。

影响瞬态响应的参数交通，通常使用以下几个参数来确定车辆瞬态响应品质，以下描述部分参数。

（1）波动时的固有频率ω0

根据方程式（7）能够得到：

固有频率ω0是评价车辆瞬态响应的重要特征参数之一。当ω0值相对高些时，车辆瞬态响应好。所示为部分欧洲及日本轿车的稳定性因素 K值与固有频率f0值关系，固有频率f0=ω0/ 2π。从图5能够看见，f0值为1Hz附近时。欧洲高速公路允许的最高车速最高，所以轿车行驶车速高，其固有频率也较高，在0.9Hz以上[3]。

图5 部分欧洲及日本轿车固有频率f0值与稳定性因素K值

（2）阻尼比ζ

由式（7）可知：

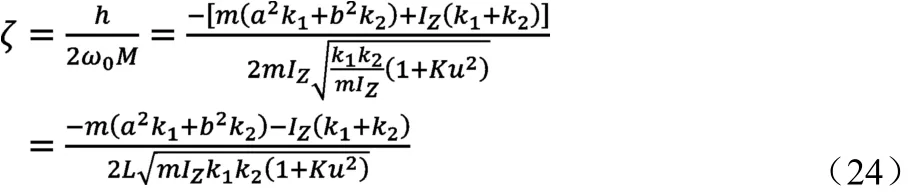
计算表明，随着车速的提高，ζ值减小；在稳定性因素K值不变的条件下，后轮胎侧偏刚度增加有助于ζ值得增大；质量、转动惯量、轴距减小，ζ值亦有所增加[4]。

德国几个大学的研究机构进行了规模较大试验，得出的结论是现代轿车超调量是ωrmax/ω0×100%=112%∼165%，试验条件是31.3m/s（70mile/h），ay=0.4g。与此相对应的阻尼ζ=0.5∼0.8[5]。

（3）反应时间τ

反应时间为车辆前轮输入转向盘角阶跃运动后，横摆角速度第首次到达稳定值ωr0所需时间。也有部分文献取到达0.9ωr0或0.63ωr0值需要的时间，被用来进行定性分析时，没有本质区别。τ也是评价车辆瞬态响应重要特征参数之一。τ值偏小时，车辆瞬态响应较好。

加下来把车辆横摆角速度响应方式（16）重新列出：

当t=τ时，

即sin（ωτ+Φ）=0

故

研究表明：当车速增长时，车辆的响应时间减小；当车辆质量增大时，轴距伸长，车辆的响应时间也相应减小；但转动惯量增加时，车辆响应时间有所增加。

（4）达到第一峰值ωr1的时间ε

车辆到达第一峰值ωr1所需时间ε通常也被用作评定车辆瞬态横摆响应品质的特征参数。ε也称作峰值反应时间。

式（16）两边同时取导数，得到：

当t=ε时，

故

德国几所大学的车辆研究机构进行了转向盘角阶跃响应试验，得到下面的统计数据：近代车辆的ε=0.23～0.59s；而质心侧偏角与峰值反应时间的乘积εβ，即汽车因素 T.B.为0.25～1.45s（°），相应的试验工况为 31.3m/s（70mile/h），ay=0.4g。Benz中型货车装备不同轮胎时，在u=20m/s，ay=0.3g的试验条件下，ε=0.94～1.72s，T.B.=2.06～4.76s（°），质心侧偏角β=2.05°～3.03°。

4 模型的仿真分析

对式（6）进行拉氏变换可得：

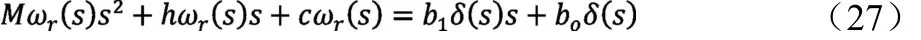
经整理得到：

方程式（28）可以被当作控制系统中的传递函数，也及时把车辆当作一个开环系统。车辆方向盘转角δ是输入激励，车辆横摆角速度ωr是输出响应。式（28）即为汽车系统的传递函数。

二自由度汽车车身参数如表1所示。

选取试验车速为30m/s，在仿真时间为0时给前轮一个阶跃信号，使前轮由 0°转到 10°，并保持不变。为考察轮胎侧偏刚度对汽车瞬态响应的影响，前、后轮侧偏刚度由－23140N/rad、-38320N/rad变为－33120N/rad、-66250N/rad。

表1 二自由度汽车模型仿真参数

图6 转向盘角阶跃输入下的汽车瞬态响应

根据汽车横摆角速度传递函数，编写绘制不同侧偏刚度下的汽车横摆角速度的时域特性曲线的MATLAB程序。运行程序，得到不同轮胎侧偏刚度下的汽车横摆角速度时域特性曲线如图 6所示。可以看出，汽车在行驶速度相同、前轮转角输入相同的情况下，较大的轮胎侧偏刚度，横摆角速度峰值变化不大，但汽车响应时间显著缩短，汽车稳定性变好。

5 结论

本文介绍了轮胎的侧偏特性，建立了汽车二自由度动力学模型，并对动力学模型进行了求解，最后应用 MATLAB对动力学模型进行了仿真分析。仿真结果表明：较高的轮胎侧偏刚度（指绝对值），能显著缩短汽车响应时间，保证汽车具有良好的操纵稳定性。