飞机螺栓双剪连接结构有限元应力分析

陈彦达 范振民 李 军

（1.东航技术应用研发中心，上海 201707；2.上海飞机设计研究院，上海 201210）

0 引言

机械紧固接头是航空航天领域中连接结构部件最常用的方法，如机翼结构中的蒙皮—梁/肋板连接、机翼—机身连接是飞机主结构中螺栓连接的典型示例。螺栓紧固件能够很好地将连接件夹紧在一起，并且具有良好的承载能力。一些研究人员[1-4]详细介绍了螺栓连接的设计方法主要是在静态载荷条件下，但是在构件上钻出紧固件孔本身会在孔附近引入应力集中并减小承载横截面积，钻孔过程也会影响紧固件孔内部的表面光洁度，这在循环载荷下容易产生疲劳裂纹。

飞机结构主要由高强度轻合金和复合材料制成，材料的低密度性能使它们成为了理想的强度/重量比航空航天材料。安全性在航天飞行器中是至关重要的，因此已经进行了大量研究，旨在优化结构螺栓连接的设计，从而防止飞行过程中的灾难性故障[5-11]。

螺栓连接通常通过初始扭矩进行预加载，当扭矩施加到螺母上时，螺栓被轴向拉伸，机械构件被夹紧在一起。以往的研究证实，当接头承受纵向拉伸载荷时，螺栓的夹紧效应可以降低螺栓孔处的应力集中，从而增加接头的断裂强度和疲劳强度[12-16]。基于有限元分析结果，发现预紧力可以在单个夹板的螺栓孔周围引入有益的压应力，且施加的预紧力越高(在一定程度内)，在孔区域的压缩应力的幅度越大，这种压应力可以减小在所施加的拉伸载荷下产生的合成应力的大小。此外，还发现在循环加载条件下，预紧力大幅度增加可能会导致配合面螺栓板的表面产生微动现象[16-17]。

随着紧固件的被夹紧，确定螺栓连接中的局部应力分布通常是三维问题，有一些方法可用来根据夹紧区域内压力分布的常规假设来估计接头构件的刚度[18-19]。Rötscher[18]提出，应力包含在接头中平面对称的两个圆锥形截面内，每个截面的顶角都是2α，然后选择α=45°的半顶角来计算刚度。在之前所述研究[9]中讨论了双圈铝制螺栓连接结构的有限元计算结果，并展示了夹紧板的整体压力分布，包括在外板上形成的一对圆锥体和一个沿中间板厚度均匀分布的中空圆柱体。据研究，有限元法是一种用来确定和分析螺栓连接的应力和应变的方便而有效的方法，然而，文献综述证实[9]，由于预紧力和拉伸载荷而引起的螺栓连接的三维应力分析非常复杂，并且还没有被进行彻底的研究。

本研究的主要目的是确定飞机双搭接铝制螺栓连接处的应力和应变分布，以便预测这种连接的失效模式。在设计和生成结构三维有限元模型后，模拟螺栓预紧力，随后在板远端施加拉伸载荷，为了改善飞机金属和复合材料结构中的螺栓连接设计，研究并讨论了孔区域产生的应力和应变结果。

1 有限元建模过程

使用CATIA三维软件设计了双搭接螺栓连接结构，结构几何形状和尺寸如图1 所示。该结构包含三块相同的铝合金7075-T6 板，厚度均为3 mm，孔的直径为5 mm，并选择直径为4.9 mm的标准航空航天螺栓紧固件(AN3-6A)来夹紧铝合金板。在本算例中，由于两个笛卡尔平面的几何结构和载荷条件是完全对称的，所以只对其四分之一进行数值分析，如图2 所示，并且为这些对称平面上的节点定义了对称位移边界条件。

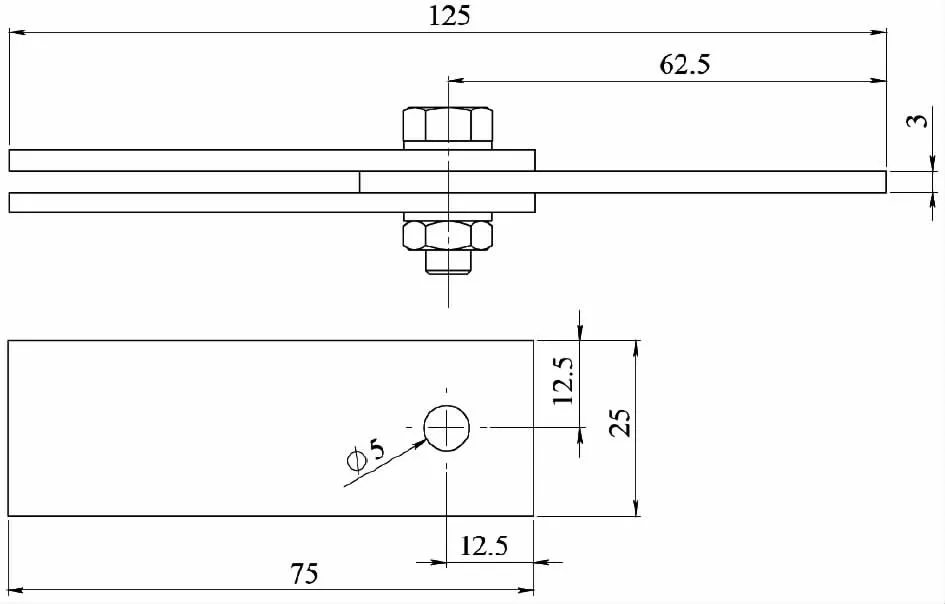
图1 接头几何及尺寸示意图 单位:mm

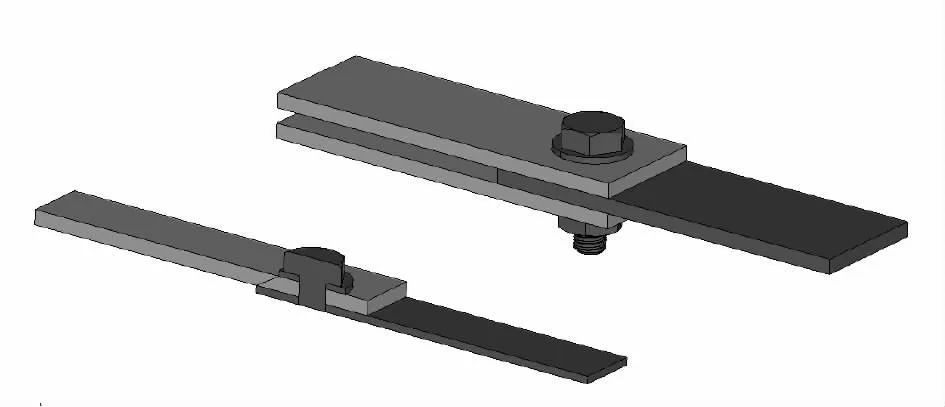
图2 结构完整模型和四分之一模型

在本文中，将螺栓的几何形状定义为圆形的螺栓头，而不是六边形。由于螺栓和垫圈的弹性模量和泊松比几乎相同，将外径为10 mm、厚度为0.75 mm的垫圈与螺栓头几何模型合并成一个整体，以减少接触单元的使用(忽略螺栓头和垫圈之间的接触)。根据参考文献[20]，受剪力接头处螺栓杆的夹紧长度应接近被紧固构件的总厚度，因此根据航空航天AN螺栓标准尺寸，螺栓建模时的紧固长度为9 mm。此外，在这里暂时不需要考虑螺纹建模，如图3 所示，假设螺栓杆和紧固件孔之间的径向间隙为0.10 mm。

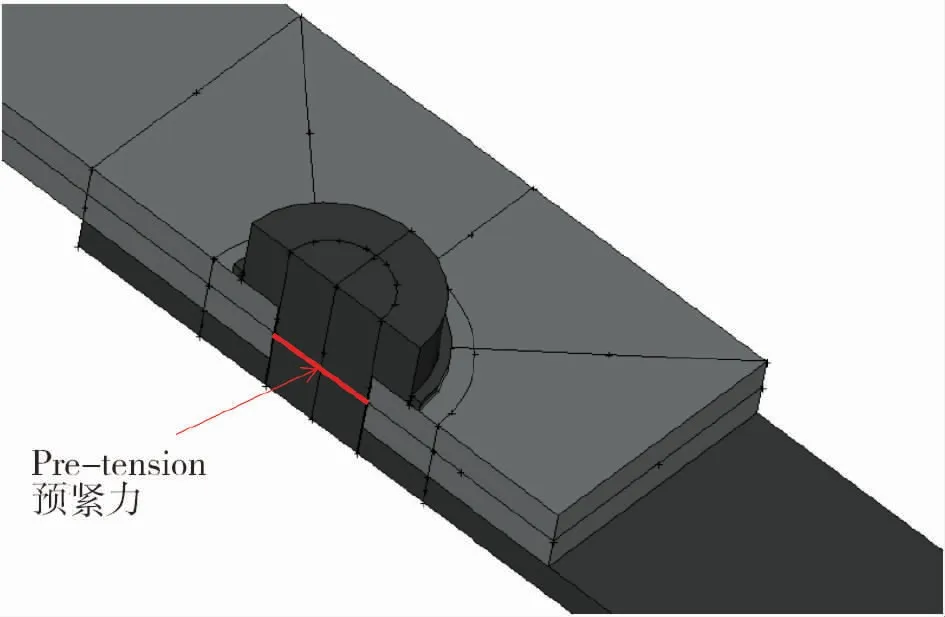
图3 预紧力模拟

为了达到最优的网格密度，对板和螺栓的几何模型进行虚拟分区，然后对单元划分进行多次修改，以实现应力计算结果的网格不敏感性。图4 显示了最终的结构网格模型。

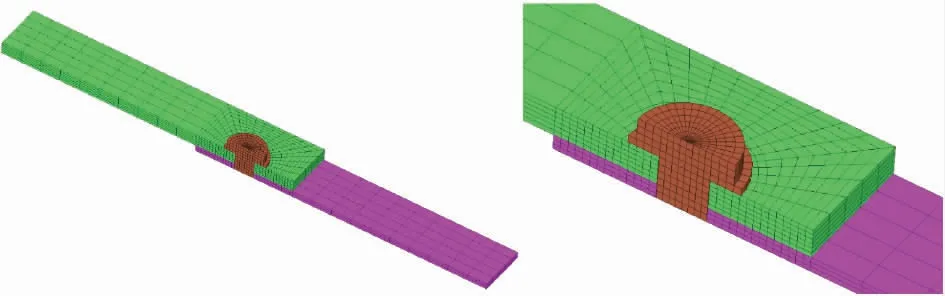
图4 有限元网格模型

由于考虑到结构将受到不同水平的纵向载荷，采用弹塑性多线性运动硬化材料模型对铝合金7075-T6 的应力—应变行为进行了表征。选择这种材料来计算材料塑性区域中的应力和应变，特别是在中间板的孔周围位置。薄铝板由于轧制过程显示出正交异性行为，在某些情况下，这种差异可以达到10%，但在本研究中给忽略了这种正交效应。铝合金7075-T6 的应力—应变曲线如图5 所示[16]，并将此图的7 个数据点作为模型材料的输入参数，如表1 所示，弹性模量和泊松比分别为E=710 GPa和v=0.33。对于钢制螺栓和垫圈，采用弹性模量为210 GPa，泊松比为0.30 的线弹性材料，这是基于所测试的数据，即螺栓材料在受到最大给定扭矩(5.5 N·m)[9]时仍处于弹性变形区域(没有塑性变形)。

图5 铝合金7075-T6 应力—应变曲线图

表1 7075-T6 应力—应变曲线数值

所有接触表面之间的摩擦系数在模型中被考虑，这里使用弹性库仑摩擦模型。将钢制螺栓(头部和柄部)与铝板之间的摩擦系数设置为0.23，顶部和中间的板之间摩擦系数设置为0.22，模型中所有接触表面之间的4 个不同的接触对如表2所示。

表2 接触对设置

接下来施加预紧力和纵向拉伸载荷，并为接头模型定义了两个不同的载荷步。实体螺栓模型作为真实的有限元模型，拉伸、弯曲等载荷通过螺栓进行传递[9，21]，参考文献[9]采用实心螺栓建模，在ABAQUS 中通过Pre-tension 来模拟预紧力(如图3所示)，预紧力大小分别为2 kN、4 kN和6 kN。之后，对于具有特定预紧力的每个待解决的模型，在接头处施加15 kN的纵向远程拉伸载荷，因此，在第二个载荷步中，相应的远程应力在x方向静态地施加到中间板的远端(远离孔)，这个压力分为15 个子步骤递增的方式施加，目的是获取所有1，2，3，...，15 kN拉力下对应的应力值的数值结果。除了对称的位移边界条件之外，顶板的端部也受到所有自由度的约束。

2 计算结果及讨论

夹紧区域内的纵向正应力有限元计算结果表明，在接头处的应力整体呈瓦片形状分布，这些结果在以前的工作中已经经过了讨论[9]。根据计算结果，预紧力的大小对接头的抗拉强度有影响，并且由中间板产生的纵向法向应力(σx)的分量大小来表示。对模型施加不同的预紧力，分析中间板最大应力在不同预紧力下的σx，如图6 所示，可以发现即使对于最大的预紧力，压缩应力也不是很大，当接头受到远端施加的纵向拉伸载荷时，这个应力分量可以起到控制合成应力的关键作用。

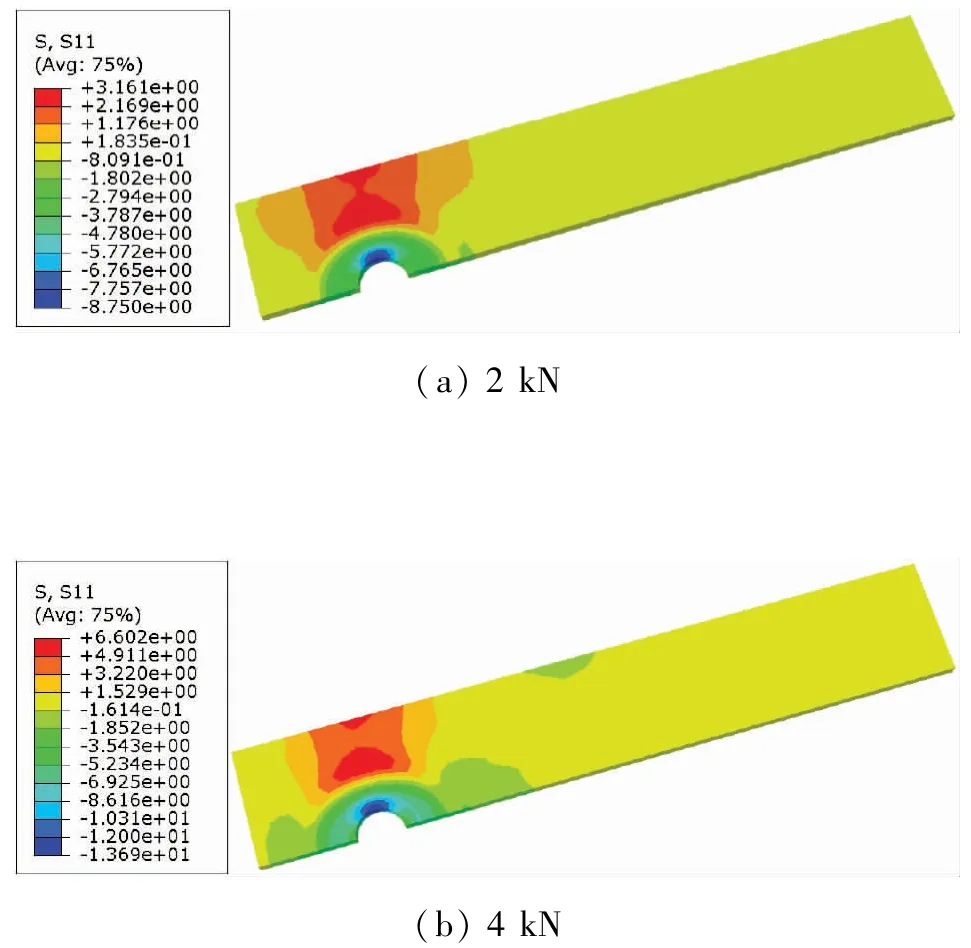
图6 中间板纵向应力σx最大值在不同预紧力作用下 单位:MPa

在对不同预紧力的有限元模型施加1，2，3，...，15 kN共15 个纵向拉伸载荷子步骤之后，对接合处进行数值分析。图7 表示在15 kN的纵向拉伸载荷和预紧力为1 kN的情况下，中间板合成纵向应力(σx)的分布图。如应力云图所示，最大拉应力位于孔的边缘处，特别是由于缺口存在而导致出现局部应力集中的中间板，这也反映了为什么在金属双搭接螺栓连接结构中的中间板容易发生破坏。另外，为了传递施加在接头上的压缩载荷，在螺杆和板之间接触的区域也存在着较大的压缩应力，在正交各向异性复合材料板中，应力结果也会受到中间板的纤维取向和叠层顺序的影响[5，10]。

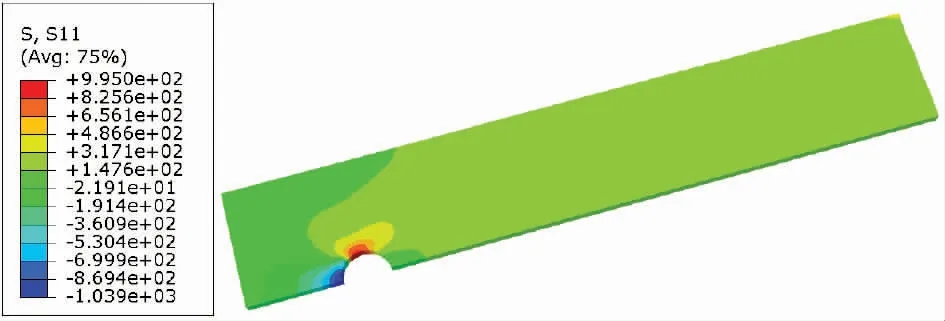
图7 中间板在1 kN预紧力和15 kN纵向拉伸载荷下的纵向应力分布(σx) 单位:MPa

根据Shankar和Dhamari[16]的研究结果，在紧固件孔附近，类似的双搭接螺栓板最终断裂发生在中间板上，图8 显示了在1.15 kN预紧力作用下，试件中间板在最大应力为144 MPa和载荷比为0.1 的循环载荷下发生的疲劳失效。不合格试件的断裂指示疲劳在应力局部集中的孔边缘开始，断裂线穿过紧固件孔的中心线。该试验与获得的有限元模拟计算结果的对比具有很好的一致性，并且验证了结构的有限元建模是合理的。

图8 试件中间板在预紧力为1.15 kN、纵向拉伸应力为144 MPa下的疲劳破坏[16]

对上述45 个模型计算得到的σx应力结果进行比较，揭示出较大的预紧力可以大大减少应力集中和孔周围的压缩应力，数据对比结果如图9 所示。例如，模型在2 kN预紧力和10 kN纵向拉伸应力作用下时，中间板孔边缘的最大拉伸应力(σx)是647 MPa；然而，当预紧力增加到6 kN时，该应力显著降低到524.2 MPa。同样的情况下，中间板孔边缘最大压缩应力(σx)从764 MPa减少到630.6 MPa。需要注意的是，在某些加载情况下，铝板的应力大小超过了材料模型应力—应变关系的极限值，这是因为在ABAQUS 中通过简单地外推曲线来分析这些大的应力和应变。

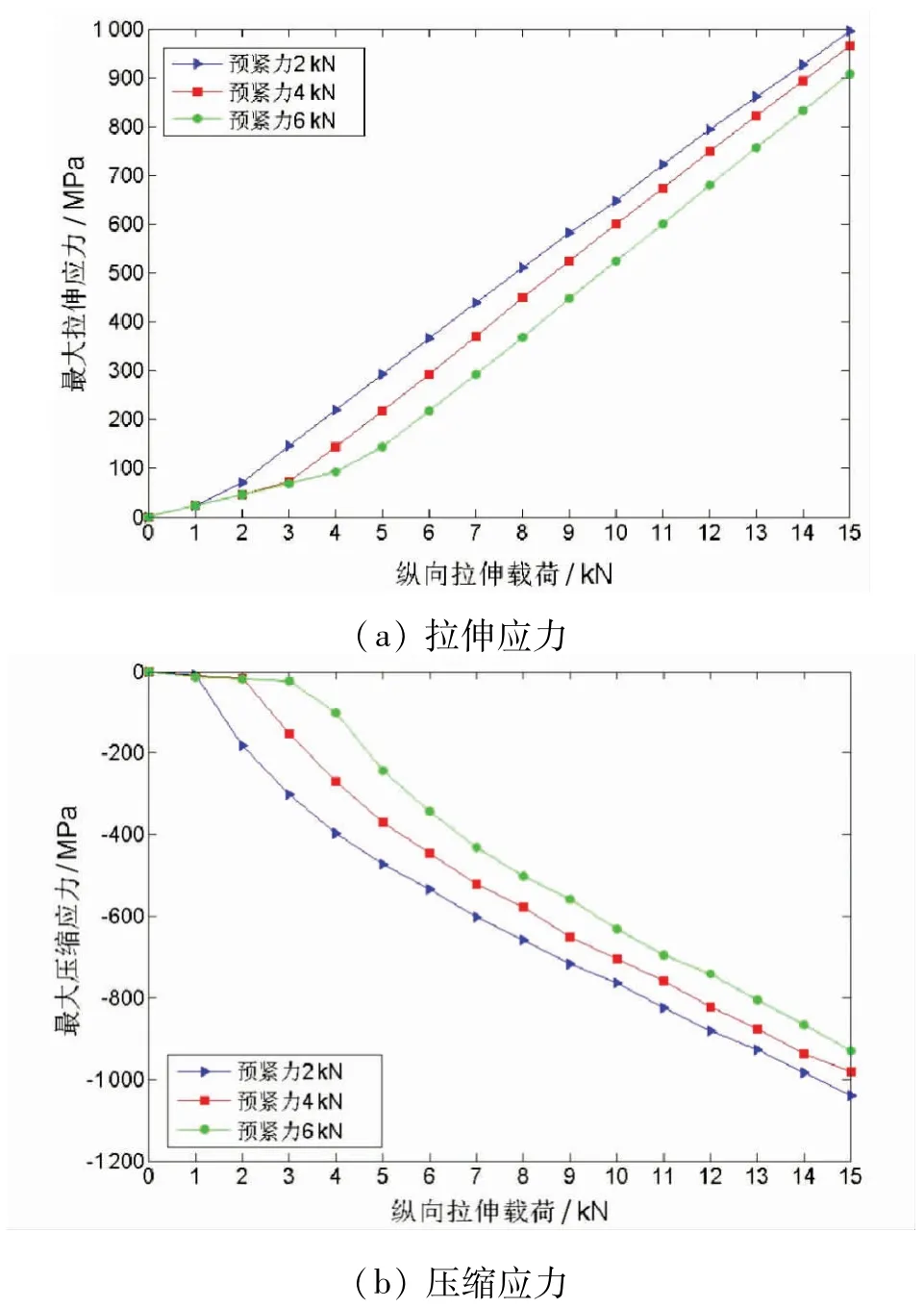
图9 在不同预紧力和纵向拉伸载荷下的中间板孔边缘处最大应力值

为了从数值上发现随着预紧力的增加可以减少局部应力，对不同预紧力模型的拉伸和压缩应力最大值的减少百分比进行了平均，结果如表3 所示，可以发现，当预紧力从2 kN增加到6 kN时，将使中间板的最大拉伸应力和压缩应力分别减小26.93%和30.42%。如之前所述，为了研究7075-T6 板受局部应力下的夹紧效应，使该结构承受不同水平的纵向拉伸载荷，在图10 中分别显示了施加2 kN和6 kN的预紧力模型，在受到9 kN纵向拉伸载荷下的Von Mises应力云图。可以发现，通过施加较高的预紧力，孔边缘的应力幅值较小，因此当施加在远离接头的纵向拉伸载荷相对较高时，塑性应变也较小，它将Von Mises塑性应变的最大值从1.32 ×10-2减少到1.05 ×10-3，共减少了12.55 倍。

表3 随着预紧力的增加拉伸应力和压缩应力的平均减少百分比

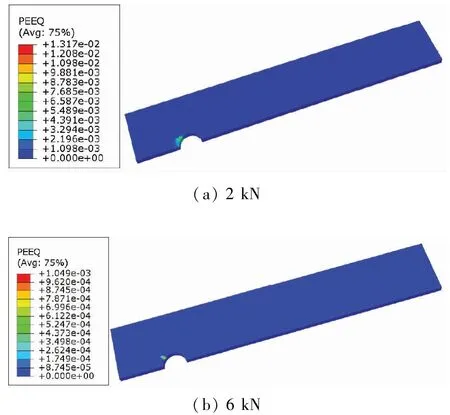
图10 纵向拉伸载荷为9 kN时，不同预紧力作用下中间板孔边缘的塑性应变 单位:MPa

此外，对于预紧力最大(6 kN)而纵向拉伸载荷较小(小于3 kN)的模型，最大拉伸应力(σx，max)出现在远离孔边缘的位置，如图11 所示。在这种情况下，可以认为由于较高预紧力所产生的压应力可以成功克服由于施加较小的拉伸载荷而导致的局部应力，因此，最大拉伸应力不一定发生在孔边缘处。实际上，通过较大的预紧力来紧固接头，产生了较大的法向力来压缩接合板，并因此在配合表面之间产生了较大的摩擦力，由于施加的纵向拉伸载荷较小，所以这些板贴合地非常紧密，因此，大部分的载荷是通过摩擦来传递的，而不是螺杆和孔边缘区域的板之间的压缩应力。

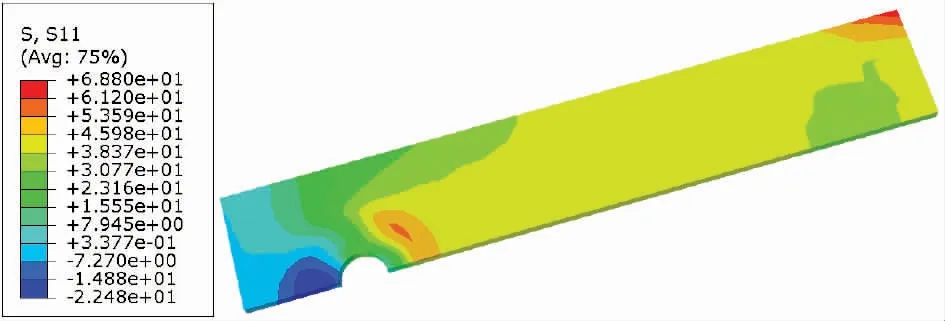
图11 在6 kN预紧力和3 kN纵向拉伸载荷下中间板的纵向应力分布(σx)及最大拉伸应力的位置 单位:MPa

高预紧力对结构承载的好处，很大程度上取决于结构之间的摩擦，但工程结构设计中，摩擦力所带来的好处通常是不允许考虑的。因此本文还计算了在没有摩擦的前提下，预紧力带来的应力变化，如图12 所示。

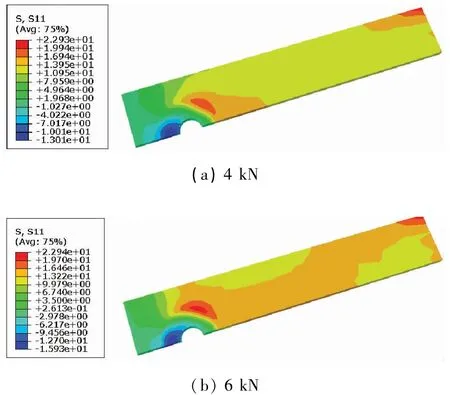
图12 不考虑摩擦且纵向拉伸载荷为1 kN时，不同预紧力作用下中间板应力 单位:MPa

通过进一步的对比发现，在不考虑螺栓和板之间的摩擦力时，当预紧力从4 kN提升到6 kN，纵向拉伸载荷为3 kN时，最大拉伸应力减少的比例为2.68%，而在有摩擦的情况下这一比例为5.1%。当纵向载荷增加到4 kN时，无摩擦和有摩擦两种条件下最大拉伸应力下降的比例分别为35.8%和35.25%。

3 结论

本文利用ABAQUS 有限元分析软件，对典型的飞机螺栓连接结构进行了三维应力和应变分析，提出了一种有限元建模技术，模拟了螺栓连接中的预紧力，根据之前的研究结果成功地验证了该方法的有效性，并对紧固件受预紧力大小的影响进行了研究，结论如下：

1)施加预紧力可以在螺栓孔周围引入有益的纵向压缩应力，从而减少孔边缘处由于局部应力集中产生的合成应力。这些应力在螺栓连接位置处更为集中，并且可以有效减小在施加远端纵向拉伸载荷下的产生的结构变形。

2)数值分析结果表明，对于在施加纵向拉伸载荷下的螺栓连接结构，较大的预紧力将更有利于降低紧固件孔边缘处的应力集中，这可以显著提高接头的拉伸强度和疲劳寿命。

3)这项研究工作证明，即使在较大的纵向拉伸载荷下，施加较大的预紧力来牢牢夹紧紧固件接头，可以通过改变结构载荷传递，将压缩应力转化为摩擦力来有效地减少紧固件孔处压缩应力的破坏效应。这可以成功地防止高负荷结构螺栓连接处的承压损坏，特别是对于主要失效机理是纤维微屈曲的组合结构中。对复合材料层压进行上述分析也将是有意义的，在进行损伤演化[22]和疲劳强度评估方面，了解贯穿整个板厚的应力幅值大小十分重要。