基于时间上下文的个性化电影推荐算法研究

张正风，唐 敏，李清秀

（徐州生物工程职业技术学院 图文信息中心，江苏 徐州 221006）

0 引言

传统的协同过滤推荐算法根据用户历史评分数据进行推荐，未充分考虑时间因素的影响。本文充分挖掘时间上下文信息在推荐算法中的影响，提出一种基于人记忆特性的协同过滤推荐算法，即 HMC-CF（Collaborative Filtering Based on Human MemoryCharacteristics）推荐算法。用户兴趣会随时间流逝而变化[1]，为了追踪用户兴趣随时间变化而产生的偏移，本文以人的记忆特性为出发点，拟合艾宾浩斯遗忘曲线得到时间衰减函数来追踪用户兴趣偏移。考虑到人的记忆遗忘特性和不同年龄阶段用户的记忆遗忘速率不同，将年龄因子融入遗忘时间衰减函数做进一步改进优化。除了遗忘规律，人看到某物品时存在回忆起相似物品的可能，这种现象被称为记忆激活。根据记忆激活理论得到时间权重函数，时间函数能够衡量用户历史行为物品对当前物品的影响权重[2]。前者侧重基于用户群的推荐，后者侧重基于产品群的推荐。综合上述两种情况，得到一种混合的评分预测方法。

1 基于记忆特性的时间函数

1.1 融合用户年龄的遗忘时间衰减函数

记忆是有时限性的，一个人能够回忆起几个小时前发生的事情的大多数细节，但对几个月前甚至几年前发生的事情只能回忆起大概。根据这种现象，可以认为在推荐算法中用户当前评分的物品价值要高于过去评分物品的价值，并且这种价值会随着时间的增长逐渐降低。[2]上下文信息中的时间信息可以直接从日志文件中提取，获取方便，所以很多研究都在推荐算法中融入时间因素来提高推荐准确率，取得了良好的效果。大多数针对时间上下文推荐算法的研究，通常设置一个时间衰减函数，用户或者物品的相关程度会随着时间增长而降低。一些专家学者从人的遗忘特性出发，拟合艾宾浩斯遗忘曲线得到时间函数，李桃迎等[3]将拟合的艾宾浩斯遗忘时间衰减函数融入到评分预测中，可以通过计算得到当前用户对物品的剩余兴趣度，即剩余评分，进一步提升了Slope One 算法的性能。艾宾浩斯遗忘曲线的数学函数公式为：

其中，f 表示初始记忆值，t 表示与当前时间间隔，c 和 k 为控制常量，且当 c 为 1.25，k 为 1.84时，函数最符合正常人的遗忘规律。考虑到记忆力随着年龄增长逐渐衰退，对公式（1）进行改进，融入用户年龄因子后改进的公式为：

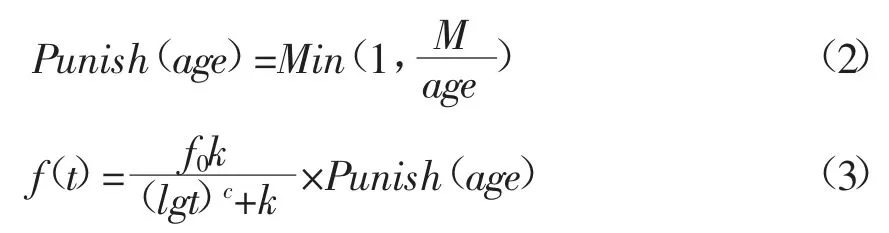
其中，age 是人的年龄，M 是设置的年龄阈值。通过融入年龄因子，时间衰减函数能够根据用户年龄进行调整，从而更加准确地追踪用户兴趣随时间变化产生的偏移。

1.2 融合概率的记忆激活时间权重函数

人看到某物品时存在回忆起相似物品的可能，心理学家Anderson[4]针对这种现象进行研究，提出了记忆激活理论。他认为人类记忆能否被激活取决于相关记忆的使用历史和当前感觉记忆同相关记忆的关联度，经过深入研究记忆激活理论，得到了基于该理论的记忆激活计算公式，设事件S为物品i 能够激活相似物品j 的相关记忆，事件S为物品i 不能激活相似物品j 的相关记忆，则有：

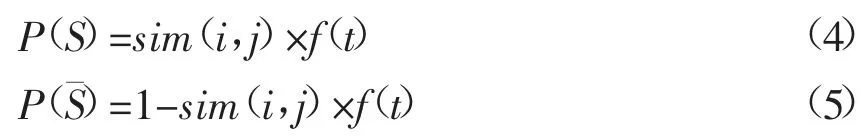
融入概率后的时间权重函数公式如下：

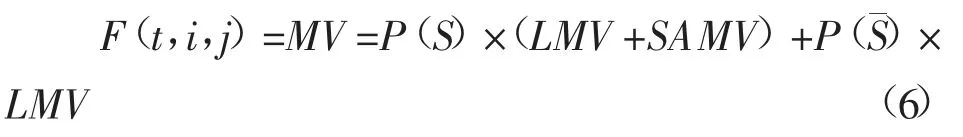
其中，i 代表当前待评分物品，j 代表历史评分物品，t 表示物品 i 和物品 j 的时间间隔。LMV 表示用户对项目的长期记忆，SAMV 表示相似项目激活的记忆值。

2 基于人记忆特性的协同过滤推荐算法

2.1 基于记忆遗忘的评分预测

根据上文给出的融合时间上下文的用户相似度计算方法，可以计算出目标用户的N 个最近邻。然后通过遍历用户评分矩阵得到最近邻用户评分而目标用户未评分的项目集合[5]，把得到的项目集合当作推荐项目候选集，最后计算出推荐项目候选集中项目的预测评分，具体表示如下：

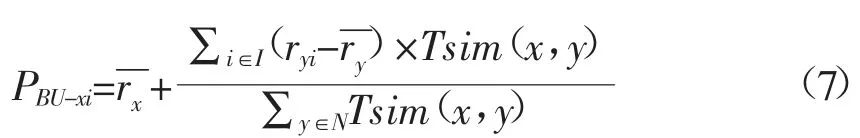
其中，PBU-xi表示目标用户x 对项目i 的预测评分，ryi表示用户y 对项目i 的评分表示用户y对其所有评分项目的平均评分，N 表示用户相似邻居集。

2.2 基于记忆激活的评分预测

根据上文提出融合概率的记忆激活时间权重函数，该函数可以计算出用户历史行为物品对当前物品的影响权重。由此，可以将该时间函数融入到用户评分预测，对用户x 有过行为的物品评分进行加权，权重值由该时间权重函数计算得到，然后对所有物品相似度的和求平均值[6]，就可以得到用户x 对物品i 的预测评分，其公式如下：

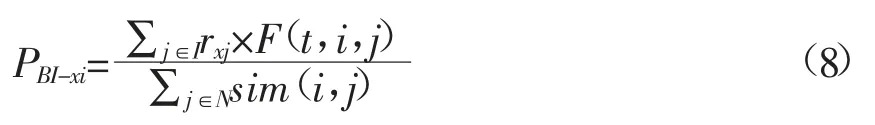
其中，PBI-xi表示目标用户x 对项目i 的预测评分，rxj表示用户x 对项目j 的评分，I 表示用户有过评分的项目集。

2.3 混合评分预测

2.1 和2.2 中分别给出了基于记忆遗忘的评分预测方法和基于记忆激活的评分预测方法。这两种评分方法侧重点不同，基于记忆遗忘的评分预测主要从用户相似度角度给用户进行推荐，而基于记忆激活的评分预测侧重于从物品之间的相关度给用户进行推荐。总的来说，前者关注用户群对目标用户的影响，后者从目标用户自身角度出发，关注历史评分项目群对目标用户的影响[7]。如果仅从相似用户群的角度进行推荐，可能存在相似用户较少或者不存在的情况，这种情况下，推荐准确率不高甚至无法进行推荐。为了避免上述情况，混合两种评分方式，当相似用户比较少时，提高基于项目群推荐的权重，能够有效地改善推荐性能，故融合基于记忆遗忘和记忆激活两种评分预测方式，得到混合后的评分预测公式如下：

λ 是调和参数，当λ=1 时，表示只考虑基于相似用户群的推荐；当λ=0 时，表示只考虑用户历史行为物品的推荐。λ 具体值根据相似用户群和目标用户历史行为物品的具体情况而定。

3 实验与分析

3.1 实验描述

3.1.1 实验环境与实验数据集

该实验运行于单机环境下，实验环境为Intel（R）Core（TM）i5-4210MCPU@2.60Ghz，内存 16G，Windows764 位 OS。实验数据集为 MovieLens，它是GroupLens 研究小组在不同时间段从MovieLens 系统上收集的电影评分数据集，数据真实有效，其中包括电影属性信息、用户人口统计学信息以及对本实验来说最为关键的电影评分信息等内容。

3.1.2 实验设计与评价标准

对MovieLens 数据集按评分时间对评分数据进行升序排序。抽取其中20%的数据作为测试集，80%的数据作为训练集。随机抽取5 组这样的训练集和测试集，分别进行试验，并将得到的5 组实验结果求和取平均值作为最终实验结果。采用对比实验方式，对比了HMC-CF 算法与UserCF、FCCF 以及MA-CF 的准确率和覆盖率[8]。

3.2 实验结果分析

3.2.1 实验参数选取

本文提出的HMC-CF 算法中有两个参数：M和λ。其中，M 是用户年龄阈值，控制用户年龄因素对推荐算法的影响，还需确定λ 的大小。这里先假设λ 的值为0.5，用户最近邻个数k=20，利用混合评分预测公式得到 M 值在 20、25、30、35、40、45、50 时的推荐评分，并计算在不同M 值下的推荐算法的MAE 值，如图1 所示。通过分析，确定M=35。采用同样的方法，确定λ=0.4，体现了综合考虑用户群和物品群的优势，提升了推荐的性能。

图1 参数M 值的选取

3.2.2 结果分析

确定HMC-CF 算法参数M 和λ 的值之后，对比 UserCF、FC-CF、MA-CF、HMC-CF 在不同最近邻个数K 下的MAE 值和在不同推荐列表长度N下推荐的准确率，实验结果如图2 所示。

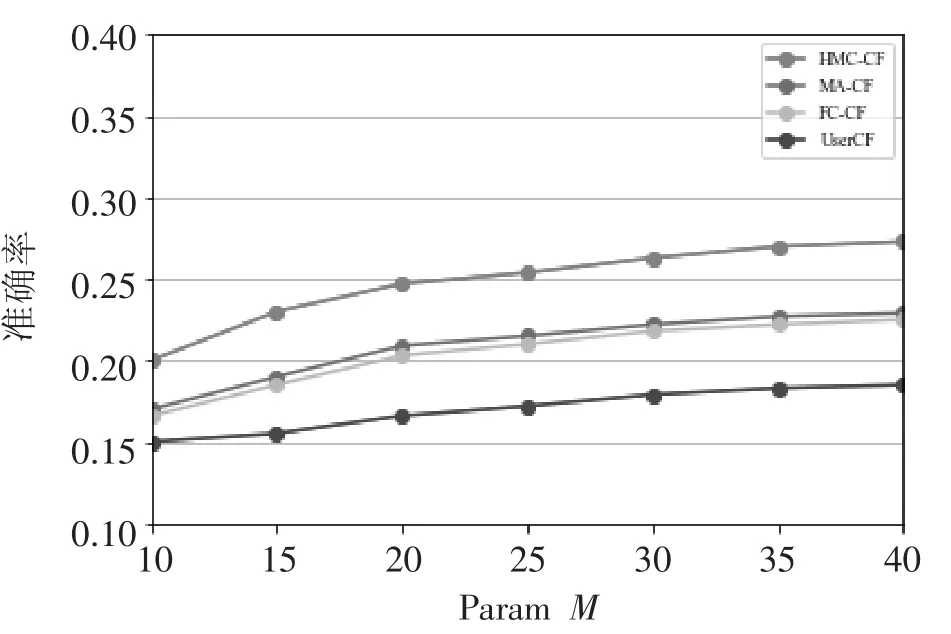
图 2 UserCF、FC-CF、MA-CF、HMC-CF 的准确率

由图2 可以看出，FC-CF 和MA-CF 算法误差和推荐准确率相差不大，但都比UserCF 的算法误差小、推荐准确率高，FC-CF 和MA-CF 仅比User-CF 多融入了时间信息，所以认为时间上下文在提高推荐算法性能上具有重要作用[9]。本文提出的HMC-CF 算法的误差又明显小于FC-CF 和MACF 算法，准确率也更高，验证了HMC-CF 算法在提高推荐准确度上更具优势。

为进一步验证HMC-CF 算法的优越性，文中对比了在不同最近邻下各算法的推荐覆盖率，结果如图3 所示。

图 3 UserCF、FC-CF、MA-CF、HMC-CF 的覆盖率

由图3 可以看出，FC-CF 算法与UserCF 算法的覆盖率相差不大，总体略低，MA-CF 比FC-CF和UserCF 略高。HMC-CF 算法在最近邻比较少时，覆盖率和 UserCF、FC-CF 以及 MA-CF 相差不大，但随着最近邻的增加，覆盖率明显高于这三种算法。分析其原因，主要是HMC-FC 算法综合考虑了用户群和产品群，同时通过项目属性计算项目相似度，也避免了活跃物品的影响，所以推荐物品覆盖率更好[10]。

综上所述，融合时间上下文信息、综合考虑用户群和项目群的推荐方式使得推荐结果更加准确、覆盖率更高，明显提升了推荐系统的性能，具有可行性。

4 结语

本文介绍了HMC-CF 算法的记忆遗忘特性和记忆激活特性。记忆遗忘特性拟合艾宾浩斯遗忘曲线，得到基于用户群的评分预测，记忆激活特性侧重用户历史行为物品的影响，得到基于产品群的评分预测。本文综合考虑两种情况，得到混合评分预测，进行对比实验，实验结果分析表明，该算法在推荐准确率、覆盖率上更具优势。