平安银行结构化理财产品定价分析

王杨 赵丹 张寄洲 傅毅

摘  要： 理财产品作为银行一种较高收益率和较低风险的投资方式，迎合了投资者的需求。以平安银行财富“结构类（100%保本挂钩利率）资产管理类开放型98天人民币002期”理财产品为研究对象，利用现金流贴现模型、LIBOR市场模型进行建模，运用蒙特卡罗模拟法，借助Matlab软件，计算出该产品的理论定价，并与平安银行的实际定价相比较，分析其合理性。得出该理财产品的预期收益率与产品说明书中提到的最高到期收益率相一致，说明该理财产品的价值被低估。

关键词： 结构化理财产品; 现金流贴现模型; LIBOR市场模型; 蒙特卡罗模拟; 定价

中图分类号： F 832    文献标志码： A    文章编号： 1000-5137（2020）05-0533-08

Pricing analysis of structured financial products of Ping An Bank

WANG Yang1， ZHAO Dan2， ZHANG Jizhou1， FU Yi1*

（1.School of Finance and Business， Shanghai Normal University， Shanghai 200234， China; 2.Mathematics and Science College， Shanghai Normal University， Shanghai 200234， China）

Abstract： As a high yield and low risk investment method，financial products cater to the needs of investors.In this paper，the financial product of Ping An Banks wealth structured （100% guaranteed linked interest rate） asset management open 98-day RMB 002 series is taken as the research object.The mathematical model is established by using the discounted cash flow model and the LIBOR market model.The theoretical price of the product is calculated by using Monte Carlo simulation.By comparing the theoretical price with the actual price，it is concluded that the expected yield of the financial product is consistent with the highest yield mentioned in the product description.This shows that the value of the financial product is underestimated.

Key words： structured financial products; discounted cash flow model; LIBOR market model; Monte Carlo simulation; pricing

0  引  言

一方面，随着我国人民个人财富的日益增长，在满足各种刚性和弹性消费需求后，人民口袋里富余的钱越来越多，这激发了人们更为强烈的投资欲望;另一方面，中国金融市场在全球经济一体化的影响下，利率市场不断走向成熟，利率市场化程度显著，这使投资者在银行传统的存款业务中获取的利润空间被进一步压缩。以前，相较于投资各类股票和证券，投资者更青睐于将资金存放于银行进行储蓄，向银行让渡出资金在一段时间内的使用权，来获取相对较为稳定的利息收益，这种收益较为可观，且承擔的风险相对较小。但随着利率市场化带来的利润空间被压缩，较低的存款利率已经难以赢得大多数投资者的青睐。在此背景下，理财产品作为银行一种较高收益率和较低风险的投资方式，迎合了投资者的需求，成为商业银行个人业务中的重要组成部分。然而，我国金融市场起步较晚，国内银行业缺乏经验，尤其在结构化理财产品的核心技术上落后于西方国家。另外，理财产品的市场定价是否真正合理，是否具有投资价值尚待验证。因此，对理财产品进行定价研究，一方面，可以为产品发行方（金融机构）在理财产品的设计、定价、创新等方面提供一定的理论参考;另一方面，还可以为产品购买方（投资者）在理财产品的认知、选择、管理等方面提供一定的投资建议。

结构化理财产品，又称为结构化产品、结构化票据以及联合证券等，它是现货市场和国际金融衍生品市场的一种创新型理财工具。运用金融工程理论，可以将结构化理财产品拆分为一个固定收益证券和一个金融衍生品的组合产品，其收益率与挂钩的标的资产紧密相关。其中，金融衍生品主要有期权、期货、远期以及互换;挂钩的标的资产则包括股价（股指）、商品（商品价格指数）、债券、信用、基金、利率、汇率等。结构化理财产品种类繁多，根据不同的标准，可将其划分成不同大类，如按照标的资产分类、期权类型分类或期限分类等。结构化理财产品的固定收益证券部分可以为投资者带来一定的固定收益，而金融衍生品部分则为投资者获取超额收益创造了可能性，该理财产品的收益率为这两部分收益率之和。

结构化理财产品的概念最早起源于20世纪七八十年代的美国，相隔10年以后，这个概念才传入亚洲。2002年，结构化理财产品第一次进入了中国市场，一年后，中国市场上出现了第一款与利率挂钩的理财产品。各国学者对结构化理财产品进行了大量的研究，核心问题是产品的定价问题。STOIMENOV等[1]对德国市场中挂钩标的为股票的结构化产品进行了研究，得出该产品存在溢价现象。BENET等[2]研究了部分反向可交易证券，发现反向可交易证券的定价被高估。CHEN等[3]将看涨的股票挂钩的理财产品与宏观政策等因素做回归分析，发现此类结构化产品的定价没有偏差。徐承龙等[4]利用偏微分方程方法研究了一类与短期利率相关的期权型外汇存款条约定价问题，当短期利率为无套利Hull-White模型时，可得出显式解，其余情况需用差分法求解近似解。汪航等[5]认为保本型股票挂钩结构类产品是结构化理财产品的一种趋势，并对设计、风险和定价等一系列问题进行了研究。崔海荣等[6]利用行为金融学相关理论研究了嵌入式障碍期权的结构化产品的设计和定价问题。陈金龙等[7]研究了多资产挂钩的结构化理财产品的定价问题。刘宗亮[8]运用产品复制技术、风险中性定价、蒙特卡罗模拟和无套利分析等知识研究了带触发条件的结构化理财产品的定价问题，选取东亚“步步为盈10”精选银行股部分保本投资产品为案例，得出该案例存在3%的溢价。万山[9]对结构化理财产品进行了系统分析，以招商银行一款理财产品为例，运用使用Black-Scholes模型和Monte-Carlo模拟，对其进行实证分析，发现Black-Scholes模型和Monte-Carlo模拟的结果是一致的，并发现该产品属于折价发行，对于投资者有利。DENG等[10]运用蒙特卡罗模拟、数值积分、分解法和偏微分方程4种方法进行了结构化理财产品的定价研究。姜艳等[11]运用非平稳时间序列条件异方差模型和蒙特卡罗模拟方法研究了农业银行“金钥匙·如意组合”理财产品。方艳等[12]运用Copula函数二分性解决资产间的相依性问题，根据多资产挂钩的标的产品收益函数特征，利用蒙特卡罗模拟方法对产品进行定价。可以看出，国内外学者主要集中在选取不同挂钩标的和改进研究方法两方面对结构化理财产品进行拓展和改进。

迄今为止，所查阅的文献中没有关于平安银行“结构类（100%保本挂钩利率）资产管理类开放型98天002期”理财产品定价的研究，此产品属于利率挂钩型结构化理财产品。本文作者以平安银行“结构类（100%保本挂钩利率）资产管理类开放型98天002期”理财产品为案例，研究其定价问题。针对该产品的结构特点运用现金流贴现模型、LIBOR市场模型进行数学建模。利用和讯网（http：//data.bank.hexun.com）关于美元即期LIBOR数据，用Lagrange插值多项式法求出各期即期利率，根据即期利率与远期利率的关系，求得所需的远期利率结构，运用Matlab软件对美元3个月的即期LIBOR未来走势进行蒙特卡罗模拟，得出该理财产品的理论价格高于其实际价格。因此参考本文模型计算结果对于投资者而言，该理财产品是具有投资价值的。

1  收益结构

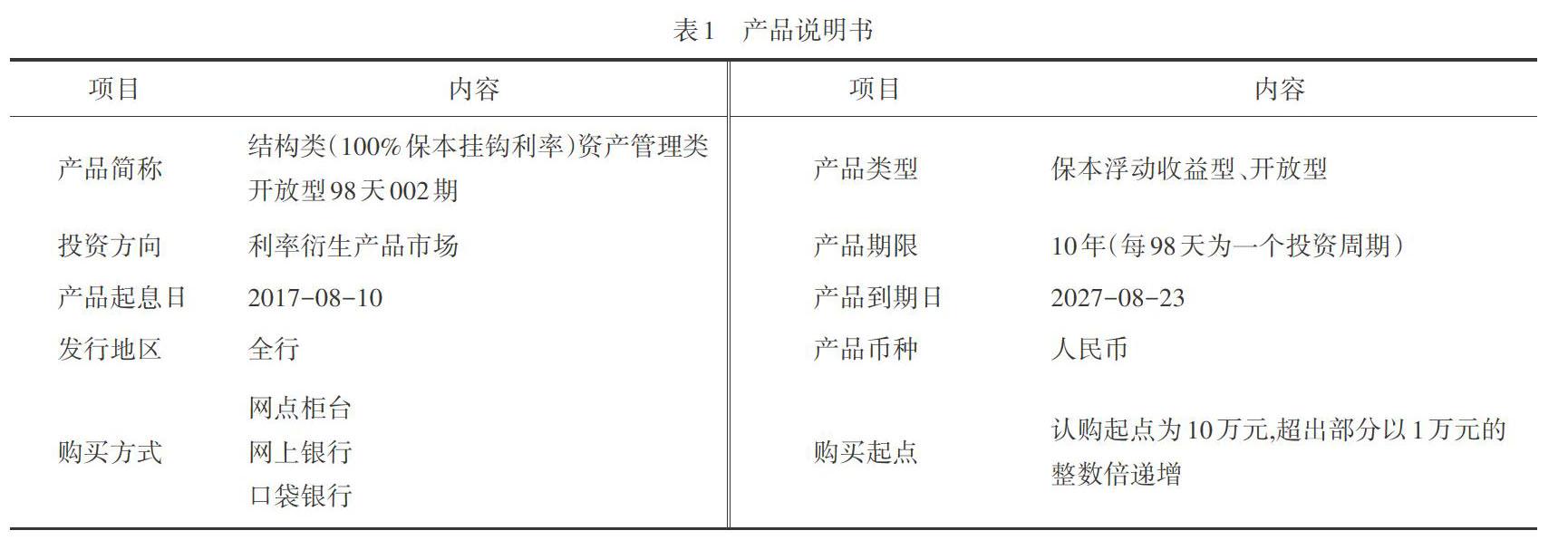
平安银行财富“结构类（100%保本挂钩利率）资产管理类开放型98天人民币002期”理财产品是98天保本浮动收益型理财产品，该产品收益挂钩于国际市场上美元3个月LIBOR。产品说明书如表1所示。

该产品的累积区间为，客户的实际（年化）收益率为固定（年化）收益率和浮动（年化）收益率两部分之和，固定的年化收益率为1.10%，浮动收益率计算公式为，计算结果精确到小数点后4位。

该结构化理财产品的收益可以拆分为固定收益和浮动收益两部分。固定收益部分是相对稳定的部分，期末收益能够可靠测量;对于浮动收益部分，产品发行时事先设定了一个累积区间，产品到期后的收益率与挂钩利率（国际市场上美元3个月伦敦银行同业拆借利率）落入设定的累积区间的天数有关，是一种典型的区间累积型利率挂钩型理财产品。因此，浮动部分的收益取决于挂钩利率在产品存续期间的整体表现。

相对应地，可以将该产品的理论价格也进行上述同样的拆分，得到该理财产品的理论定价为：

其中，代表固定收益部分的理论定价，代表浮动收益部分的理论定价。

2  定价模型

該产品的定价由两部分构成：固定收益部分和浮动收益部分，本小节将分别讨论这两部分的定价。

2.1 固定收益部分定价

固定收益部分定价类似于债券的定价，利用现金流贴现模型[13]，将未来债券可以产生现金流的贴现值来评估该债券的价值，即固定收益部分的价值。公式如下：

其中，为现金流到达的时间，为本金，为时期的利息，为期限，为市场贴现率。结合我国实际情况及案例特点，以上海银行间同业拆借利率（SHIBOR）作为市场贴现率。

2.2 浮动收益部分定价

浮动部分的收益取决于挂钩利率在整个存续期间的整体表现，其大小依赖于整个存续期间的即期LIBOR的大小，因此，在对浮动部分进行定价时，需要对该产品存续期内每日LIBOR可能的变化轨迹进行模拟，从而确定在整个存续期内标的利率处于累积区间的天数。接下来利用LIBOR市场模型对浮动部分进行定价，此模型可以直接观察远期LIBOR的动态变化。

假设理财产品的整个存续期为，将其进行等分，得到个节点，依次记为。在时，将到期间的远期利率记为，换言之，表示在时刻，以为起始日、为期限的远期利率。特别地，当时，表示的就是即期利率。具体地，在时刻，期限为3个月的即期LIBOR，可表示为。由于一般银行理财产品的产品周期大部分以“天”为单位，所以将3个月按照通常研究惯例，取定为90天，即。

在时刻，时刻之前的远期利率早已在国际市场上公布，故对于时刻之前的远期利率并不需要进行模拟，只需到相关网站查询即可。事实上，投资者更为关心的是未知的、时刻之后的远期利率，因此，对于期限固定的情况，在时刻，所需考察的远期利率的结构为，，…，。随着时间的推移，由变为，远期利率结构便变为，，…，。继续下去，当时间由变为时，远期利率结构变为，…，。以此类推，就可以得到时刻对应的远期利率结构，其含有个表达式，具体情况详见表2。表2中对角线上的数据，，…，就是不同时刻对应的即期LIBOR数值。

设和对应的即期利率为和，即期利率与远期利率的关系式如下：

根据LIBOR市场模型[14-15]，美元3个月即期LIBOR利率的远期结构为：

其中，为来自正态分布的随机样本，为时间间隔，为远期利率的漂移项，为远期利率的波动率。

3  实证分析

3.1 固定收益部分

依据产品说明书可知，该产品的认购起点金额为10万元，超出部分以1万元的整数倍递增，所以，不妨规定一个单位是1万元人民币。选取SHIBOR在2019年2月8日的3个月利率2.900 0%作为贴现率，根据固定收益部分定价模型（1）式，可以计算出固定收益部分的理论定价为：

3.2 浮动收益部分

由于平安银行“结构类（100%保本挂钩利率）资产管理类开放型98天002期”理财产品是以98天为一个周期，即，将这段时间进行98等分（即），以此来考察未来98天中每一天的美元3个月LIBOR。挂钩的利率为美元3个月LIBOR，即。确定了具体的、和之后，相应的远期利率结构如表3所示。

在时刻，1天后期限为90天的远期利率为，再过1天对应地变为，即所要考察的未来第1天的3个月即期LIBOR。同样地，在时刻，2天后期限为90天的远期利率为，再过1天对应地变为，再过1天后，也就是到了第2天，对应地变为，即所要考察的未来第2天的3个月即期LIBOR。按同样的递推方法（递推过程如表3箭头所示），可以由时刻的远期利率结构，依次得到未来第1天、第2天、……、第98天的3个月即期LIBOR。

将时刻的远期利率结构：，，…，确定为输入变量，可以利用即期利率和远期利率之间的关系式（2）式来确定上述数值。例如，在时刻，未来第2天期限为90天的远期年化利率计算方法为：，其中，和分别表示期限为92天和2天的即期利率。由于市场上的即期LIBOR若无特殊说明，均指年利率，故将具体的天数除以360来转化为年数。

至此，问题便转化为获取计算时需要用到的期限1～188天的即期利率数值。对此，可以用期初时刻（即2017年8月10日）美元的即期LIBOR市场报价，利用“隔夜”“1周”“2周”“1月”“2月”“3月”“4月”“5月”“6月”和“7月”的即期LIBOR市场报价的相关数据，运用Lagrange插值多项式法[16]求出。

通过对和讯网2017年8月10日美元即期LIBOR相关数据的查询，发现“2周”“4月”“7～11月”的相关数据缺失，故将考察周期扩展到“12月”，得到数据如表4所示。

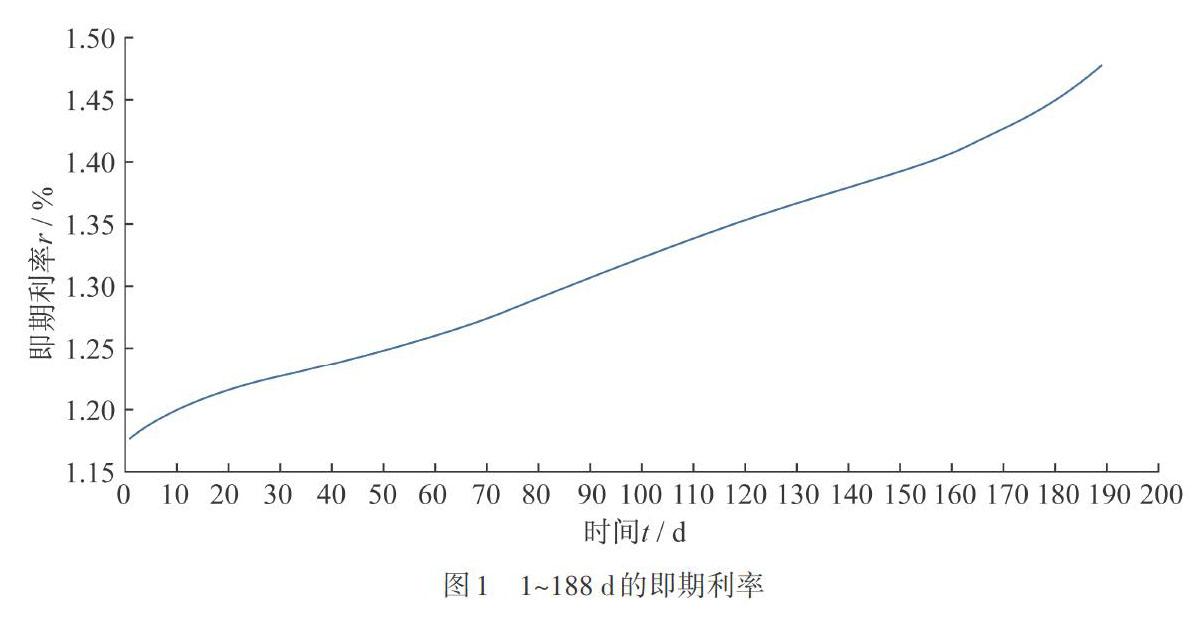
求出后，套用公式（2），即可得到时刻的远期利率结构 如图2所示。

要想使用公式（3），还需求得各期远期利率的波动率。由于本文作者所研究产品的时间周期较短，故利用该理财产品起息日前1个月内的远期利率的历史波动率来作为公式（3）中所需的波动率。采用上述求出时刻（2017年8月10日）的远期利率结构，，…，同样的方法，可以求出产品起息日前1个月（即2017年6月29日—2017年8月9日）每日的远期利率结构，，…，。将每天的一组数（共99个）整理入excel文件中，每个共有30个数据，利用STDEV公式得到对应的波动率。

最后，运用Matlab软件，利用蒙特卡罗模拟方法对利率路径进行模拟。公式（3）中选取远期利率的漂移项，，则未来第1天的即期LIBOR为：

未来第2天的即期LIBOR 需要两步计算：

未来第3天的即期LIBOR需要三步计算：

以此类推，在计算未来第天的即期利率时，需要经过次迭代。计算完98个对应的即期利率之后，便得到了3个月LIBOR的一种可能的变动轨迹，完成了第一次可能情况的模拟。之后，改变随机数的数值，可进行再一次的路径模拟。

4  结 论

经过1 000次的蒙特卡罗模拟估算出美元3个月的即期LIBOR未来可能的变化路径（图3），其全部落在该产品事先设定的累积区间之内，投资者预期获得的投资年化收益率为4.5%，这与产品说明书中所提到的最高收益率的表現情况完全一致。

平安银行相同储蓄金额（10 000元）的3个月的存款收益率为1.1%左右，可见，相较于储蓄，投资者选择该理财产品进行投资能够获取更大的投资收益。另外，由图3可知，美元3个月的即期LIBOR数值突破该产品设定的利率累积区间上限的可能性非常低，因此，投资者有较大可能性获得该产品预计的最大收益率。从投资者的角度来看，该产品的实际收益率远高于同时期的市场基准利率，价值被低估，该产品具有一定的投资价值。受限于模型结构和数据等，本研究的模型并未考虑市场流动性等因素，将在未来研究中对模型继续改进，结论也将得到进一步完善。

参考文献：

[1] STOIMENOV P，WILKENS S.Are structured products ‘fairly priced？An analysis of the German market for equity-linked instruments [J]. Journal of Banking and Finance，2005，29（12）：2971-2993.

[2] BENET B，GIANNETTI A，PISSARIS S.Gains from structured product markets：the case of reverse-exchangeable securities（RES） [J].Journal of Banking and Finance，2006，30（1）：111-132.

[3] CHEN K C，WU L.An anatomy of bullish underlying linked securities [J].Global Finance Journal，2007，18（1）：34-46.

[4] 徐承龙，周晶，任学敏.一类期权型外汇存款的套利分析 [J].同济大学学报（自然科学版），2007，35（7）：994-997.

XU C L，ZHOU J，REN X M.Arbitrage analysis of a class of deposit product with option style [J].Journal of Tongji University （Natural Science），2007，35（7）：994-997.

[5] 汪航，李飞.我国股票挂钩型银行理财产品定价分析 [J].海南金融，2009，248（7）：80-83.

WANG H，LI F.Pricing analysis of Chinese equity-linked financial products [J].Hainan Finance，2009，248（7）：80-83.

[6] 崔海蓉，何建敏，胡小平.结构性金融产品的最优设计与定价：基于发行者与投资者视角 [J].中国管理科学，2010，18（4）：8-13.

CUI H R，HE J M，HU X P.Optimal design and pricing of structured finance products：from the perspective of both issuers and investors [J].Chinese Journal of Management Science，2010，18（4）：8-13.

[7] 陈金龙，任敏.多资产的股票挂钩保本型理财产品定价研究 [J].管理科学学报，2011，14（11）：63-70.

CHEN J L，REN M.Study on pricing financial products with guaranteed equity-linked structure based on the multi-asset [J].Journal of Management Sciences in China，2011，14（11）：63-70.

[8] 刘宗亮.带触发条件结构性理财产品的定价研究 [D].成都：西南财经大学，2013.

LIU Z L.Pricing Research of Structured Financial Products with Trigger Conditions [D].Chengdu：Southwest University of Finance and Economics，2013.

[9] 万山.商业银行结构性理财产品的定价研究 [D].昆明：云南财经大学，2014.

WAN S.Research on the Pricing of Structured Financial Products of Commercial Banks [D].Kunming：Yunnan University of Finance and Economics，2014.

[10] DENG G，HUSSON T，MCCANN C J.Valuation of structured products [J].Journal of Alternative Investments，2014，16（4）：71-87.

[11] 姜艳.中国农业银行“金钥匙·如意组合”理财产品风险与定价分析 [D].泰安：山东农业大学，2017.

JIANG Y.Risk and Pricing Analysis of “Golden Key and Ruyi Combination” of Agricultural Bank of China [D].Taian：Shandong Agricultural University，2017.

[12] 方艳，张元玺，刘津智，等.多资产挂钩的结构性理财产品定价研究 [J].复旦学报（自然科学版），2018，57（5）：554-564.

FANG Y，ZHANG Y X，LIU J Z，et al. A study of pricing for structured financial products linked with multi-asset [J].Journal of Fudan University（Natural Science），2018，57（5）：554-564.

[13] 中国证券业协会.证券投资分析 [M].北京：中国金融出版社，2012.

Securities Association of China.Analysis of Securities Investment [M].Beijing：China Financial Publishing House，2012.

[14] 杨秋平.利率挂钩型结构化理财产品定价研究 [D].成都：电子科技大学，2013.

YANG Q P.The Pricing of Interest Rate Lined Structured Financial Products [D].Chengdu：University of Electronic Science and Technology，2013.

[15] 蒋承，郭黄斌，崔小勇.利率衍生品的定价研究：基于LIBOR市场模型 [J].金融理论与实践，2010（2）：3-9.

JIANG C，GUO H B，CUI X Y.Research on the pricing of interest rate derivatives based on LIBOR market model[J].Financial Theory and Practice，2010（2）：3-9.

[16] 沈燮昌.多项式插值（一）：Lagrange插值 [J].数学进展，1983，12（3）：193-214.

SHEN X C.Polynomial interpolation（1）：Lagrange interpolation [J].Advances in Mathematics China，1983，12（3）：193-214.

（責任编辑：冯珍珍）