胶质阻尼隔振器的力学模型及隔振性能研究

余慕春，赵 鹏，牛智玲，李炳蔚，南宫自军

(1. 中国运载火箭技术研究院，北京100076；2.南京航空航天大学机械结构力学及控制国家重点实验室，南京210016)

振动控制一直是航空航天、轨道车辆等工程领域的重点问题之一，新型减振技术也一直是研究热点[1−5]。纳米微孔功能材料是由水和含纳米级孔道的疏水多孔材料混合而成的新型减振缓冲材料，利用水分子在高压下进、出疏水纳米微孔并储存、释放能量的原理实现隔振、缓冲[6−7]。由于纳米微孔功能材料特殊的工作机理，可提供非线性刚度特性和优异的减振性能，因此近年来受到关注[8− 10]。

常见疏水微孔材料包括沸石、疏水硅胶、金属骨架材料等。根据卸载时水逸出疏水微孔压强的差异，纳米微孔功能材料被分为胶质阻尼(Colloidal damper)[2]和分子弹簧(Molecular spring)[6]两种。在压缩纳米微孔功能材料过程中，水在特定高压下会侵入疏水微孔，而卸载时，对于胶质阻尼，水逸出疏水微孔的压强远低于进入疏水微孔的压强，在加载卸载过程产生较大迟滞，并消耗大量能量；而对于分子弹簧，水逸出疏水微孔的压强接近于水进入疏水微孔的压强，在加载卸载过程几乎不产生迟滞，类似于无阻尼弹簧。

文献[11−13]对分子弹簧的静、动力学特性进行了较为全面的研究，而胶质阻尼的研究进展相对滞后，Suciu 等[2]研究了研究了疏水硅胶纳米微孔内的液体微流，基于接触角迟滞原理阐释了胶质阻尼的工作机理；Eroshenko[14]利用疏水硅胶颗粒和水的混合介质的高耗能特性设计多种结构形式减振器，Kong 等[15]研究了各种添加剂对胶质阻尼性能的影响，Liu 等[16]还将胶质阻尼充入金属蜂窝结构的空腔内，用以改善其缓冲特性，赵鹏等[7]根据试验结果开展了胶质阻尼的静力学建模。目前对胶质阻尼的研究主要集中在微观工作机理研究和应用初步探索，缺少对其力学模型和动力学特性的研究，无法对胶质阻尼隔振器定量设计和减振性能预计提供足够支撑，限制了胶质阻尼的工程应用。

本文设计了一种活塞液压缸式胶质阻尼隔振器，首先通过准静态和动态加载获得了胶质阻尼隔振器的迟滞特性，并研究了加载频率、振幅对迟滞曲线的影响；之后建立了包含三次非线性刚度、粘性阻尼特性和干摩擦阻尼特性的胶质阻尼隔振器力学模型，以实测动态加载迟滞曲线为基础开展了模型参数识别；最后完成了胶质阻尼隔振器的隔振性能评估。研究表明，胶质阻尼隔振器具有良好的低频隔振性能和大阻尼特性，在设备减振领域具有良好的应用前景。本文的研究将对胶质阻尼减振器性能优化设计和工程应用提供重要支撑。

1 胶质阻尼隔振器的动态加载试验

1.1 胶质阻尼隔振器设计

为测试胶质阻尼的准静态力学性能，本文设计了一种活塞液压缸式胶质阻尼隔振器如图1所示。胶质阻尼缓冲器缸体主体直径70 mm，高273 mm，活塞直径为10 mm，液压缸容积为24 mL。试验所用纳米微孔功能材料采用疏水硅胶颗粒，如图2所示，通过在硅胶颗粒表面嫁接C18基团(18-烷基氯硅烷)的方法获得疏水性，颗粒平均粒径为50µm，材料孔径为6 nm；试验过程中液压容器内疏水硅胶颗粒充填量为5 g。

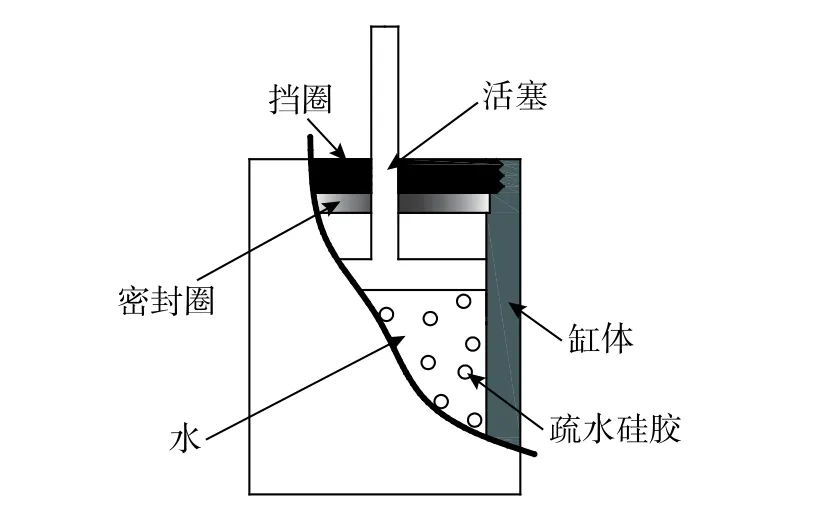
图1 胶质阻尼隔振器结构Fig.1 Structure of colloidal damper isolator

图2 疏水硅胶颗粒Fig.2 Hydrophobic silica gel particles

1.2 准静态加载试验

通过电液伺服疲劳试验机对胶质阻尼进行准静态加载，如图3所示，胶质阻尼隔振器固定在疲劳试验机上，加载和卸载速度均控制为0.2 mm/s。

图3 加载试验装置Fig.3 Test rig

加载卸载循环如图4所示，由于材料的疏水性，水在较低压力下无法克服毛细管力进入疏水微孔，这个阶段为纯水压缩的阶段，此时胶质阻尼具有极高刚度；当压强逐步增加时胶质阻尼进入工作区，水逐渐克服毛细管力时大量进入疏水微孔，胶质阻尼刚度迅速降低；直到所有微孔饱和后，在次进入纯水压缩阶段，胶质阻尼刚度再次增大；卸载过程与加载过程相反。由于接触角迟滞原理，卸载时毛细管力远小于加载时的毛细管力，因此加载卸载过程中出现显著迟滞现象。

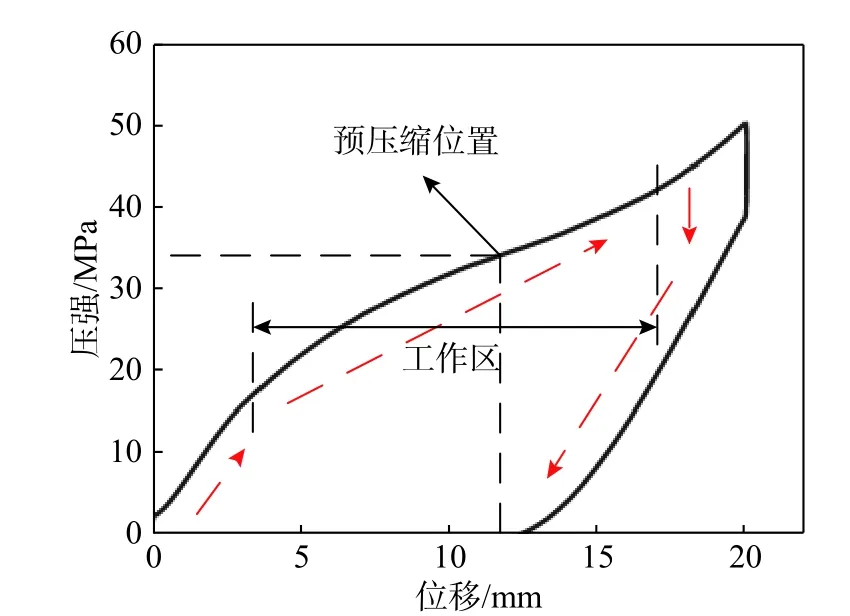
图4 准静态加载卸载循环Fig.4 Quasi-static loading-unloading hysteresis

1.3 动态加载试验

通过夹头对胶质阻尼减振器施加采用正弦输入信号x=Asin(2πft)，其中x为位移信号，t为时间。通过试验测得阻尼器在不同位移激励下的恢复力特性，从而得到减振器的迟滞特性。

为使动态加载过程中胶质阻尼尽量保持在工作区，在试验时，首先将胶质阻尼隔振器压缩至图4中预压缩位移(约12 mm)，之后对胶质阻尼隔振器施加正弦激励。振幅分别取1.5 mm、2 mm和2.5 mm，频率分别取1.5 Hz、1.75 Hz 和2.0 Hz。在不同频率，不同幅值的情况下，位移激励和回复力实测信号都十分类似。图5给出了幅值为2 mm、频率1.75 Hz 位移激励和回复力的实测时域信号。由于疲劳试验机采用位移控制，因此位移曲线为标准正弦曲线，胶质阻尼隔振器的回复力包括弹性回复力、胶质阻尼自身阻尼力和干摩擦阻尼力，因此回复力出现畸变不再是完整正弦。从图中可以看出，由于活塞和轴套之间的摩擦力，导致回复力的时域响应在方向转换时存在显著衰减情况。

另外，需要说明，振幅的选择主要遵循减振器的工作段范围，当振幅过大时，会导致减振器进入承载段和限位段刚度，或是进入两种刚度的结合处，无法充分体现胶质阻尼减振器在工作段的刚度和阻尼特性。而频率的选择主要受疲劳试验机加载频率的限制，加载频率过高，会导致输出位移信号的稳定性较差。同时减振器活塞和轴套之间属于金属配合，过高的频率也会导致两者之间磨损较为严重，无法得到稳定的动态回复力。

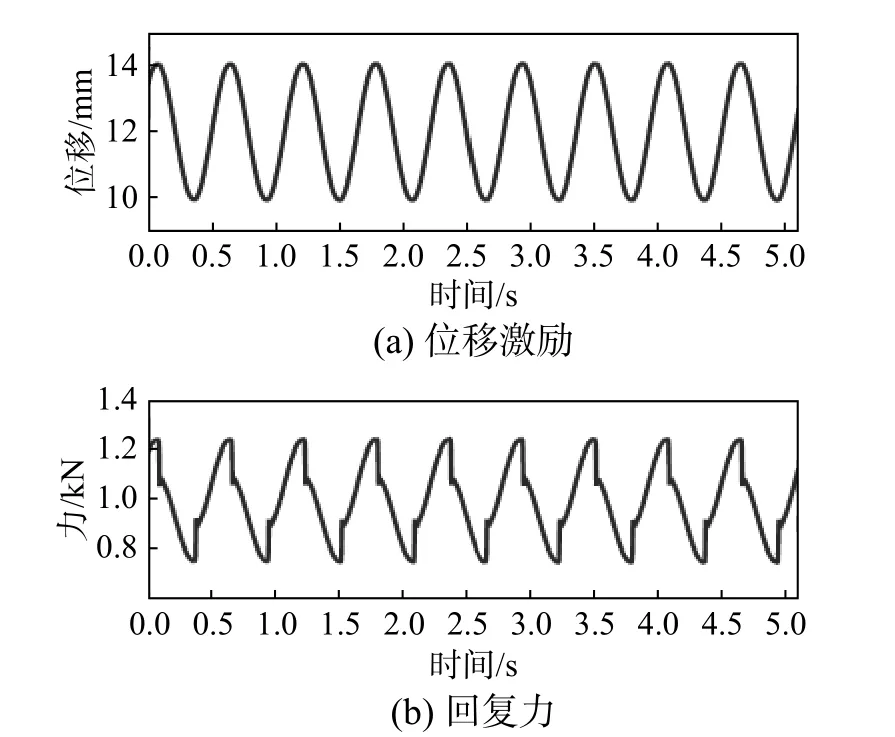
图5 时域响应Fig.5 Time domain responses

图6给出了胶质阻尼减振器等幅变频迟滞曲线，加载幅值分别为1.5 mm、2.0 mm 和2.5 mm，加载频率f分别为1.5 Hz、1.75 Hz 和2 Hz。从图6可以看出，胶质阻尼减振器等幅变频的动态力滞回曲线仅有微小差异，因此加载频率对胶质阻尼迟滞曲线影响不大，这与文献[17]中结论是一致的。

图7给出了胶质阻尼减振器的等频变幅迟滞曲线，加载频率分别为1.5 Hz、1.75 Hz 和2.0 Hz，幅值分别定为1.5 mm，2.0 mm 和2.5 mm。从图中可以看出，当加载幅值1.5 mm 时，滞回曲线斜率较小，表明减振器在小幅振动时动态刚度较小。且随着振幅增加，减振器动态刚度略有降低并趋于稳定。分析认为可能是运动方向变化时需要克服较大的静摩擦力，在振幅较小时对动态刚度影响较大。

为了进一步研究减振器的阻尼构成，向容器中添加纯水，可以得到未填充疏水硅胶时结构的激励位移和恢复力响应，根据得到的系统响应和恢复力，绘制迟滞环，此时迟滞环主要是由于结构阻尼引起的。图8对比了胶质阻尼隔振器和填充纯水时的迟滞环曲线，由图中可以明显看出，添加疏水硅胶后，系统动态力迟滞环的面积增大，说明胶质阻尼减振器不仅存在疏水硅胶材料带来的阻尼，还包括了由于干摩擦带来的结构阻尼。

图6 相同加载幅值不同加载频率的试验结果Fig.6 Experimental hysteresis with different frequencies under equal excitation displacement

2 胶质阻尼隔振器的力学建模

2.1 参数识别模型的建立

根据胶质阻尼的结构形式、准静态和动态试验结果可知，胶质阻尼隔振器包含弹性回复力、密封结构引起的摩擦阻尼和胶质阻尼材料迟滞引起的阻尼。

目前针对干摩擦阻尼的数学模型主要有两种，即理想干摩擦模型(Coulomb摩擦模型)和滞迟干摩擦模型[18−19]。理想干摩擦模型认为一个具有干摩擦交接面的单自由度系统中，交界面上的干摩擦力是突然发生的；滞迟干摩擦模型考虑摩擦交接面之间的弹性作用，胶质阻尼的干摩擦模型更接近理想干摩擦模型，其摩擦力变化规律可表示为：

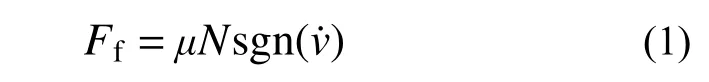
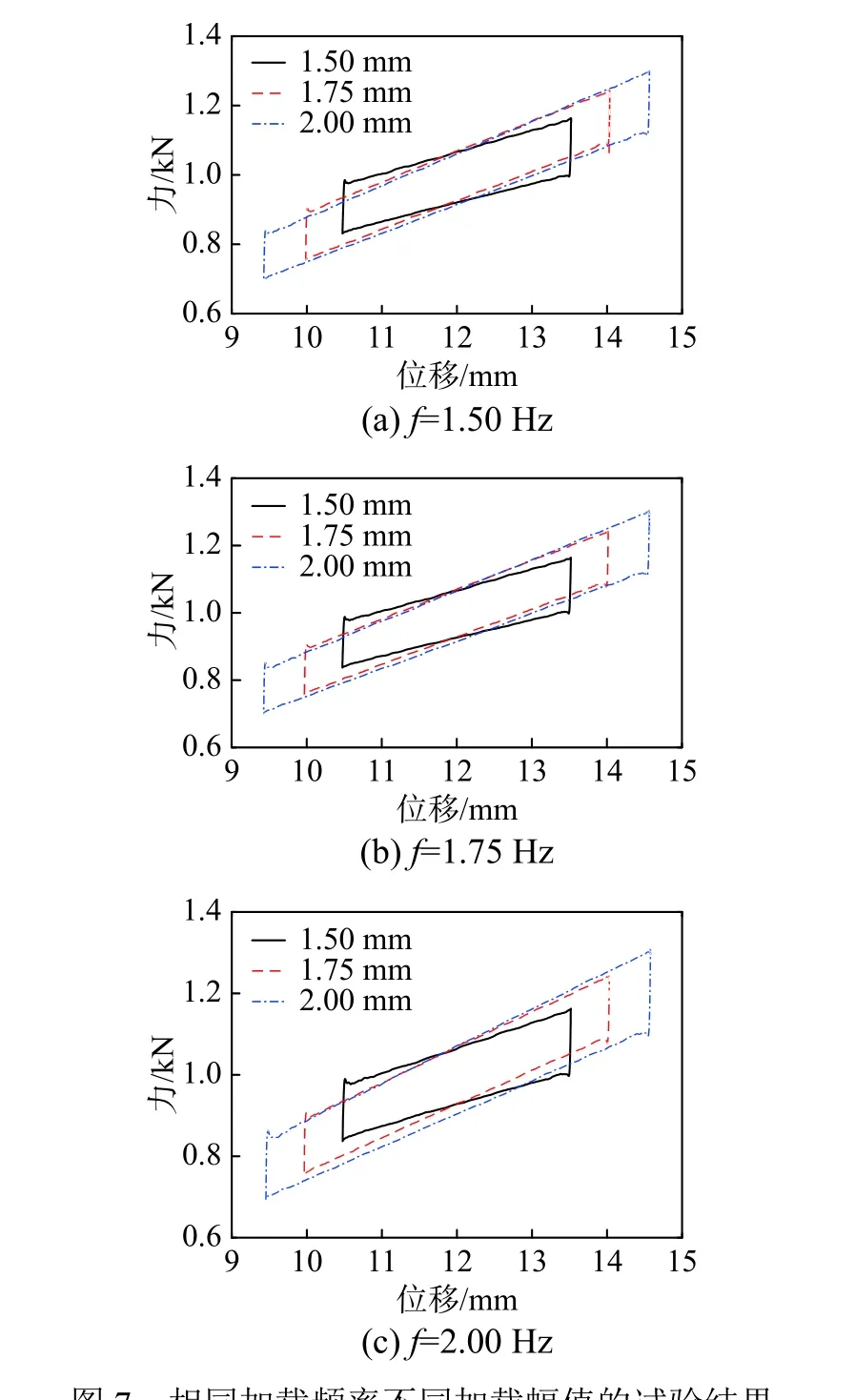
图7 相同加载频率不同加载幅值的试验结果Fig.7 Experimental resultswith different excitation displacements under equal frequency

图8 胶质阻尼和纯水的迟滞环对比Fig.8 Hysteresisof colloidal damper and pure water

为简化模型，采用理想的粘性阻尼模拟胶质阻尼材料迟滞引起的阻尼，考虑胶质阻尼和分子弹簧工作机理和准静态刚度曲线的相似性，采用三次非线性弹簧模拟胶质阻尼的弹性回复力。建立如图9 所示的参数识别模型，胶质阻尼减振器的回复力分解为三个力学单元：非线性弹簧、摩擦力单元和粘性阻尼器，分别对应胶质阻尼隔振器的弹性回复力、密封结构引起的摩擦阻尼和胶质阻尼材料迟滞阻尼。胶质阻尼减振器的恢复力可写为：

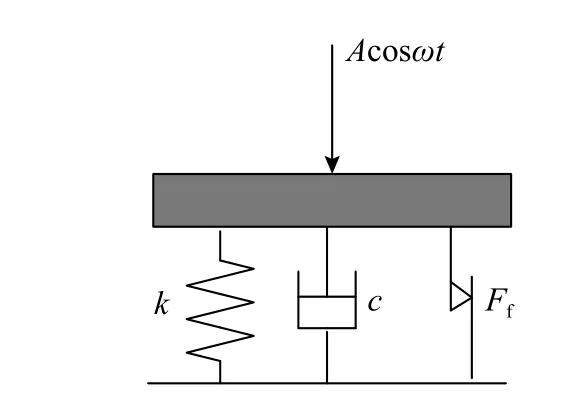
图9 胶质阻尼减振器参数识别模型Fig.9 Model of colloidal damper for parameter identification

2.2 参数识别结果

利用动态加载实测数据开展模型参数识别，模型的预测误差定义为：

式中，m是用于辨识的数据采样点数。

为了能准确获得辨识的模型参数，要求式(5)表示的目标函数最小，这是个最小乘优化问题，用Levenberg-Marquardt 算法迭代求解。

图10～图12给出了不同幅值、不同激振频率下的实测结果和参数识别结果迟滞特性，可以看出，两者具有较好的一致性。

由胶质阻尼减振器等幅变频试验结果可知，同一振幅不同频率下胶质阻尼迟滞曲线一致性较好，从参数识别的结果来看，在每一组激振幅值下，所得到的模型参数也都大致相同。因此表1中选取激振频率为2.0 Hz 的工况作为典型工况，给出了不同激振幅值下的参数识别结果。

图10 振幅1.5 mm 参数识别结果Fig.10 Resultsof parameter identification (A=1.5 mm)

根据胶质阻尼减振器的准静态试验结果，对工作段进行拟合得到弹性恢复力的参考值为k1=7.898×104N/m，k3=3.834×107N/m3。由表1可见，当激振幅值为2.0 mm 和2.5 mm 时，减振器的动态刚度接近准静态刚度。当激振幅值为2.0 mm时，参考值和辨识参数值之间的相对误差分别是2.1%和3.6%；当激振幅值为2.5 mm 时，参考值和辨识参数值之间的相对误差分别是3.7%和7.6%。这两种情况下，参考值和辨识参数值之间的相对误差均较小，说明了理论模型的合理性。同时可以看出，在三种激振幅值下，线性粘性阻尼系数c和干摩擦系数Ff的识别结果十分接近，因此在后续的隔振性能分析中，取线性粘性阻尼系数c为2543 N·s/m，干摩擦力Fc为270 N。

3 胶质阻尼隔振器的隔振性能

以图9所示的第一类隔振(隔力)为例分析胶质阻尼的隔振性能，对于这类隔振系统，其设备是振源。建立胶质阻尼减振器的振动微分方程为：

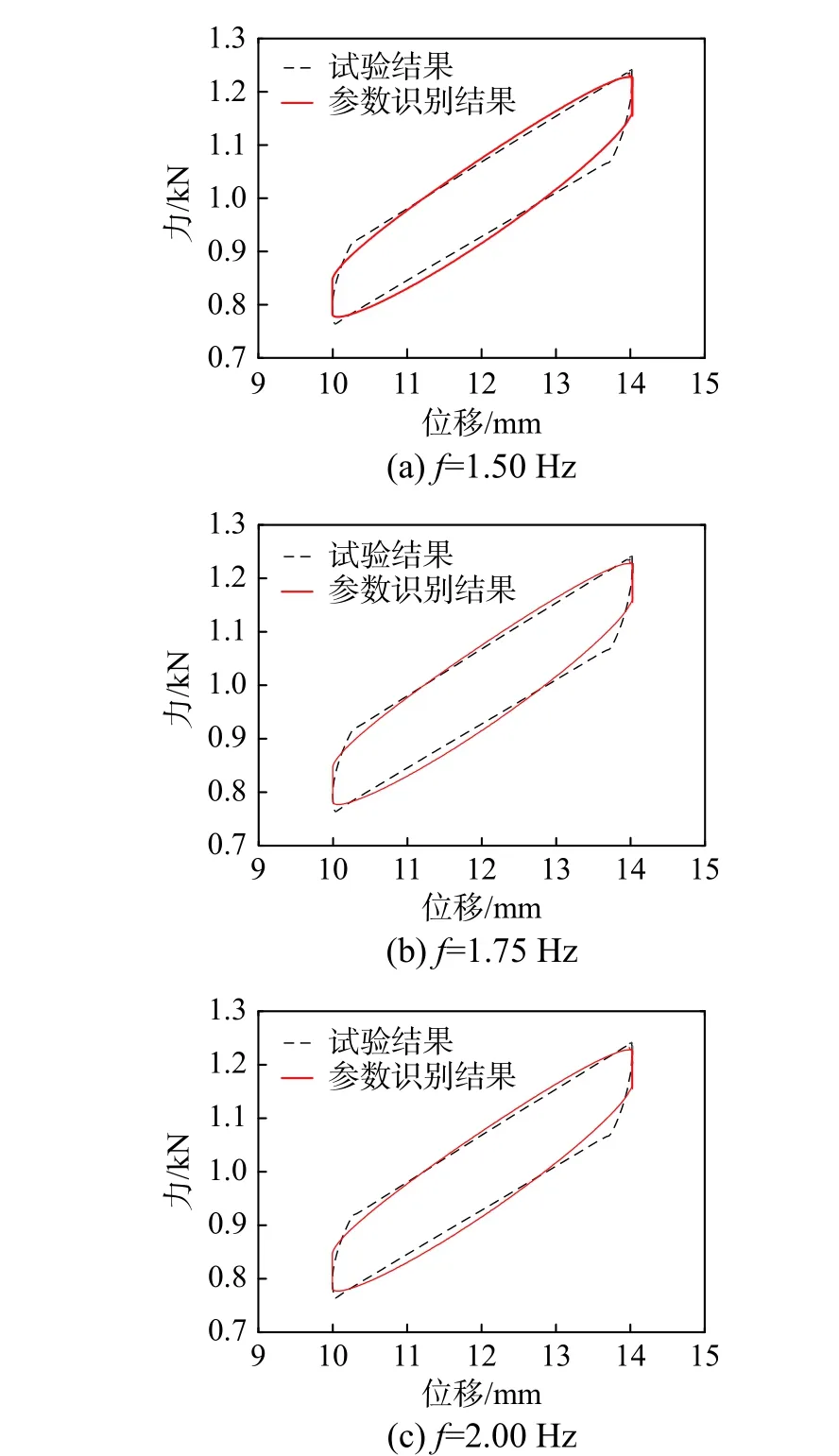
图11 振幅2.0 mm 参数识别结果Fig.11 Results of parameter identification (A=2 mm)

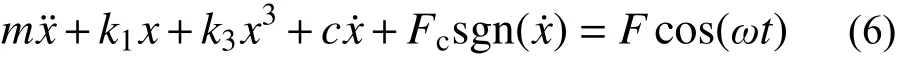
式中，F为激励力幅值。

对于非线性隔振系统，可采用文献[8]中力传递率作为指标评价其隔振性能。即：

式中，ft和f分别是系统的回复力和激励力，尽管在文献[8]中η 被称为能量传递率，其本质其实是平均意义上的激励力和回复力的关系，因此η 认为是广义的力传递率。

对于胶质阻尼减振器，回复力可表示为如下的分段函数：

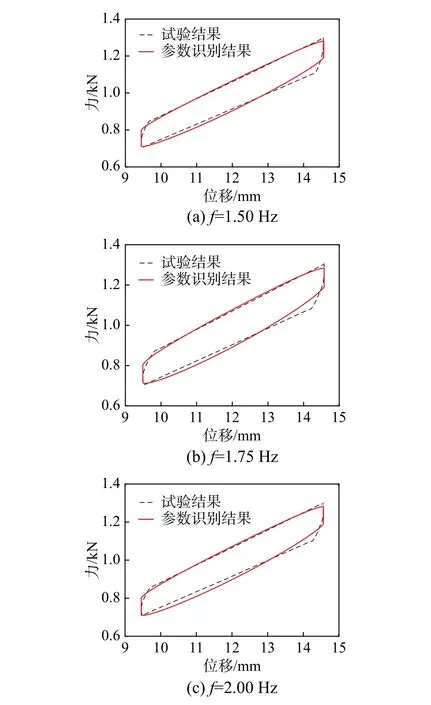
图12 振幅2.5 mm 参数识别结果Fig.12 Results of parameter identification (A=2.5 mm)

表1 激振频率为2.0 Hz 时的参数识别结果Table 1 Identified parameters(f=2 Hz)

其中，N是采样点数。根据力传递率的定义，在η<0的频率范围内系统开始有隔振效果。

基于图9所示的胶质阻尼减振器隔振模型，对隔振系统在频域的力传递率进行了计算分析。为保证胶质阻尼隔振器具有发挥良好减振效果，一般要求隔振系统静平衡状态下胶质阻尼隔振器处于工作区，本文隔振系统负载质量为M=275 kg，此时隔振器内部压强为35 mPa，静平衡位置压缩量约为12 mm，与1.3节中动态加载试验预压缩量基本一致。在振动过程中，为避免隔振器处于拉伸状态，因此一般容许振幅不超过静平衡状态的压缩量(12 mm)。首先用数值仿真(四阶定步长Runge-Kutta 方法)计算分析频带内若干频率点的时域响应，并用这些响应计算式(9)所示的恢复力，代入式(10)得到各个激振频率下隔振系统的力传递率。胶质阻尼隔振器参数为，c=2543 N·s·m−1，k1=7.734×104N·m−1，k3=3.973×107N·m−3，Fc=270 N。

图13给出了胶质阻尼减振器的力传递率曲线。从力传递率曲线还可以看出，胶质阻尼减振器的共振频率为2.8 Hz，胶质阻尼减振器在3.9 Hz进入隔振区胶质阻尼表现出良好的阻尼减振效果。此外，胶质阻尼隔振器还呈现刚度渐硬的非线性特性。

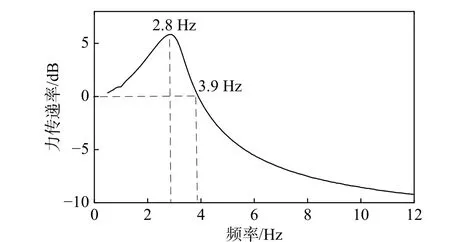
图13 胶质阻尼隔振器的力传递率Fig.13 Forcetransmissibility of colloidal damper isolator

为进一步研究胶质阻尼材料自身阻尼特性，排除结构干摩擦阻尼的影响，图14给出了去除干摩擦阻尼项的胶质阻尼减振器的力传递率曲线。对比包含和不包含干摩擦阻尼项的力传递率曲线，可以发现在共振区域内，干摩擦阻尼能够降低系统的力传递率，抑制系统的共振峰值，但进入隔振区后，隔振频率区的力传递率随着干摩擦力的存在而增加。存在干摩擦阻尼时，系统在整个分析频率内传递率均未达到−10 dB，但不存在干摩擦阻尼时，系统在6.7 Hz 附近传递率达到−10 dB。

图14 考虑干摩擦和不考虑干摩擦情况下的力传递率曲线Fig.14 Force transmissibility with and without dry friction

图15和图16对比了无干摩擦阻尼的胶质阻尼隔振器和线性隔振器的刚度曲线和隔振性能，在相同静位移情况下，尽管存在刚度渐硬的效果，胶质阻尼隔振器的固有频率仍低于对应线性减振器固有频率，在低频减振具有更大优势。此外，当共振峰值相同时，对应的线性隔振系统阻尼比为47.6%，可见胶质阻尼具有大阻尼特性，在阻尼减振领域中具有广阔的前景。

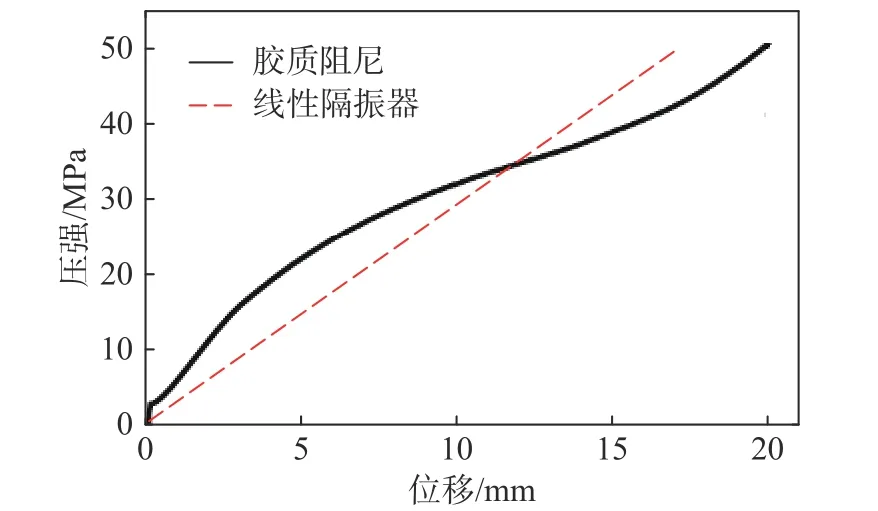
图15 胶质阻尼隔振器和线性隔振器刚度曲线对比Fig.15 Stiffness of colloidal damper isolator and linear isolator

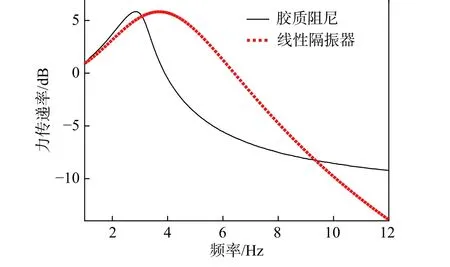
图16 无干摩擦胶质阻尼隔振器和线性隔振器减振性能对比Fig.16 Force transmissibility of colloidal damper isolator and linear isolator without dry friction

4 结论

本文通过准静态和动态加载试验获得了胶质阻尼的迟滞曲线，之后建立了包含三次非线性刚度、粘性阻尼特性和干摩擦阻尼特性的胶质阻尼隔振器力学模型，以实测动态加载迟滞曲线为基础识别胶质阻尼模型参数，并完成了胶质阻尼隔振器的隔振性能评估。结论如下：

(1)加载频率对胶质阻尼的性能几乎没有影响，振动幅值对胶质阻尼的性能有一定影响，随着振幅增大，胶质阻尼性能趋于稳定；

(2)胶质阻尼隔振器具有非线性刚度特性，因此在相同静变形下其固有频率低于线性隔振器，具有良好的低频隔振性能；

(3)由于独特的耗能机理，胶质阻尼具有优越的阻尼性能，仅需填充5 g 硅胶材料等效阻尼系数可达47.6%，因此在设备阻尼减振领域具有广阔应用前景。