双轴受压状态下的高延性纤维增强水泥基复合材料本构模型

陈善富，陈静芬，杨凤祥，刘志明

(暨南大学力学与建筑工程学院“重大工程灾害与控制”教育部重点实验室，广州510632)

高延性纤维增强水泥基复合材料(Engineered Cementitious Composites，简称ECC)是一种高性能水泥基复合材料。ECC纤维掺量低且在受拉和受压时具有高延性的特点，同时因其良好的准应变硬化特性和多缝开裂特性，被广泛应用于桥面板、桥面连接板、建筑防震抗震构件、混凝土保护层等实际工程中[1]。

1992年，密歇根大学的Li等[2]根据细观力学和断裂力学的理论，在水泥基体中添加短纤维研制出具有高延性的水泥基复合材料ECC。在我国，众多研究ECC的学者将其命名为高延性纤维增强水泥基复合材料[3−7]。

自ECC面世以来，国内外学者对其力学性能进行了大量的试验研究[8−17]，主要集中于单轴拉伸、单轴压缩、弯曲和剪切等方面。试验研究[8−17]表明，ECC因纤维桥联作用而具有良好的拉伸，压缩和弯曲韧性，同时具有良好的裂缝控制能力和耐久性。

有限元分析是对工程结构进行设计和研究的重要手段，要对一种材料的工程结构进行有限元分析需要该材料的本构模型。但是，目前的大型通用有限元程序(如ANSYS,ABAQUS等)的材料库中，尚未拥有ECC的本构模型。在对ECC 结构构件进行有限元分析时，一些学者仍然采用有限元程序材料库中现有的混凝土本构模型[5,18−19]。因此，开发一种能够较准确地体现ECC力学行为的本构模型对推动ECC在工程结构中的广泛应用具有重要意义。

为了对ECC结构构件进行有限元分析，许多学者提出了能够用于预测ECC 力学行为的本构模型。Han 等[20]提出了一种基于总应变的正交各向异性二维旋转裂缝模型模拟ECC在循环荷载下的力学响应，该模型分别定义了受拉和受压时的滞回行为，且被吸收进OpenSees地震工程模拟软件的材料库中，便于对ECC构件在承受地震作用时的力学行为进行模拟。但是，二维模型存在受形状、加载方式和边界条件限制的缺点。为了克服上述缺点，Hung等[21]在Han 模型[20]的基础上发展了一种ECC的三维本构模型，并编写了本构模型的用户自定义材料子程序UMAT嵌入LS-DYNA中描述ECC的力学行为，同时建立ECC冲切板与两跨连续梁的三维有限元模型进行数值计算，数值计算结果与试验结果较吻合。张晓悦等[22]基于Rots[23]旋转裂缝理论，提出了一种ECC的三维本构模型，该模型通过断裂能来判断裂缝平面的旋转，通过模拟ECC单轴受拉和四点弯曲试验，得到了与试验较吻合的结果。

上述三种模型都是基于弥散裂缝理论，假定ECC 由于在加载方向开裂后的材料性质与未加载方向的材料性质不同而转化为正交各向异性的材料，较好地模拟出ECC在多轴受力状态下的力学响应。但由于目前对ECC的压缩试验研究还是主要集中于单轴压缩试验，上述模型判定材料受压破坏的强度参数也仅来源于从ECC单轴压缩试验得到的单轴应力-应变曲线中：Han 等[20]根据Kesner等[24]的ECC单轴压缩试验结果采用双线性的应力-应变关系描述ECC的单轴受压行为；Hung 等[21]根据ECC单轴压缩试验结果[25]采用三线性的应力-应变关系描述ECC的单轴受压行为；张晓悦等[22]用一条非线性的Hognestad 抛物曲线[26]来描述ECC的单轴压缩应力-应变关系的上升段，其强度参数取自Yoo等[27]的ECC单轴压缩试验。

目前，对于ECC受压行为的试验研究主要集中于单轴压缩试验。除了上述三种模型所引用的ECC 单轴压缩试验外，一些学者对不同配合比的ECC 进行了单轴压缩试验，得到了不同配合比的ECC 单轴压缩应力应变曲线，并采用不同的曲线方程进行拟合：徐世烺等[28]采用二次抛物线形式描述其上升段，采用双折线形式描述其下降段；姜海军等[29]采用过镇海[30]提出的混凝土本构方程描述其上升段，采用Sargin[31]提出的混凝土本构方程描述其下降段；李艳等[11]用两个非线性的方程分别拟合了其上升段和下降段；Zhou 等[15]用线性和非线性组合的分段形式描述其上升段，用双折线形式描述其下降段。

上述三种模型中判定ECC 受压破坏的强度参数皆取自ECC单轴压缩试验，认为ECC在某一方向达到单轴抗压强度则该方向发生受压破坏。然而，现有的ECC双轴试验结果都表明[32−34]，ECC在承受双轴压应力时，一个方向上的抗压强度是受其垂直方向上压应力的大小影响的。这是由于ECC 在双轴受压时，一个方向上的压应力会对其垂直方向上的压应力所引起的侧向变形产生一定程度的约束，限制了内部微裂缝的发展，从而提高了其垂直方向的抗压强度，导致其垂直方向的应力应变关系与单轴受压时不同。另外，文献[33]研究了ECC 在单轴受压和双轴受压时的应力-应变曲线的非线性特性，并拟合了ECC在不同双轴压应力比下的应力-应变全曲线方程。因此，若在本构模型中不考虑ECC在双轴受压时的非线性应力-应变关系和抗压强度变化，就不能准确地预测ECC在承受不同双轴压应力时的力学行为。

要在本构模型中同时考虑ECC在双轴受压状态下因应力比的不同而产生的非线性应力-应变关系和抗压强度的变化，显然各向同性本构模型无法展现上述行为。Darwin 和Pecknold[35−36]为了展现混凝土在双轴受压时的非线性应力-应变关系和抗压强度变化，提出了一种混凝土的二维非线性正交各向异性本构模型。该模型假定混凝土在相互垂直的两个加载方向上为正交各向异性材料，并采用Kupfer 双轴强度包络线[37]来预测不同双轴应力比下混凝土两个正交各向异性方向上的抗压强度的变化，通过引入等效单轴应变的概念将混凝土单轴的应力-应变关系扩展到正交各向异性两个方向上，能够同时考虑混凝土在双轴应力状态下的强度变化和非线性应力-应变关系，从而能准确地描述混凝土在双轴应力状态下的力学行为。文献[23]的试验研究表明，在双轴受压状态下ECC 两个加载方向上的非线性应力-应变关系和抗压强度是随着双轴压应力比的变化而变化的，且变化规律与混凝土相似。所以，为了在本构模型中展现ECC上述力学行为，可以建立ECC在两个相互垂直的加载方向上的正交各向异性本构关系，然后通过引入双轴强度准则的方式考虑ECC两个加载方向上的强度变化。

因此，本文的主要目的是开发一种能够同时体现ECC 在双轴受压状态下的非线性应力-应变关系和抗压强度变化的本构模型，嵌入有限元分析程序ABAQUSv6.14中，用于预测ECC在双轴受压状态下的非线性应力-应变关系和抗压强度变化。本文建立了本构模型的控制方程，推导了本构模型的显式数值算法，采用Fortran 语言编写该算法的用户自定义材料子程序UMAT，并嵌入大型通用有限元分析软件ABAQUSv6.14中，通过对ECC试件的双轴受压试验进行有限元分析验证了所开发的本构模型的有效性。

1 双轴受压状态下的ECC本构模型

本文提出的双轴受压状态下的ECC本构模型能够描述ECC在双轴受压时的非线性力学行为和抗压强度变化的特点。模型包含：1)ECC在两个相互垂直的加载方向的二维增量型正交各向异性本构关系，适合于在有限元程序中采用增量-迭代法求解非线性问题[38]；2)一条非线性的受压应力-应变曲线用于描述ECC双轴受压时两个加载方向上展现的非线性力学行为；3)一条双轴强度包络线用于描述ECC 双轴受压时两个加载方向上的抗压强度变化。

1.1 ECC二维增量型本构关系

针对ECC双轴受压时展现的非线性特性，在每一增量步内建立ECC 在两个垂直加载方向上的二维增量型正交各向异性本构关系为：

为了将单轴应力-应变曲线扩展为双轴应力状态下的应力-应变曲线，这里采用文献[35]的方法，引入等效单轴应变的概念。等效单轴应变是由实际应变消除泊松比效应得到的假定值，没有实际的物理意义。但有必要指出的是，本研究通过引入等效单轴应变有利于采用应力-等效单轴应变的形式来分别描述ECC 在1、2方向上的受压应力-应变关系，并通过该关系式求解任意应力状态下1、2方向的切线模量。

式中，k为增量步总数。

式(9)表明在模型的数值算法中，1、2方向上等效单轴总应变 εui是加载过程中每一增量步等效单轴应变增量dεui的总和。

1.2 ECC受压应力-应变曲线

图1 ECC 压缩应力-应变曲线示意图Fig.1 Illustration of compressive stress-strain curve of ECC

本文将文献[33]拟合的ECC受压应力-应变多项式曲线方程扩展到引入等效单轴应变后各方向上的应力-等效单轴应变关系，如图2所示，表达式为：

通过将式(11)的 σi对 εui求导可求得式(2)中1、2方向的切线模量Ei(i=1,2)：

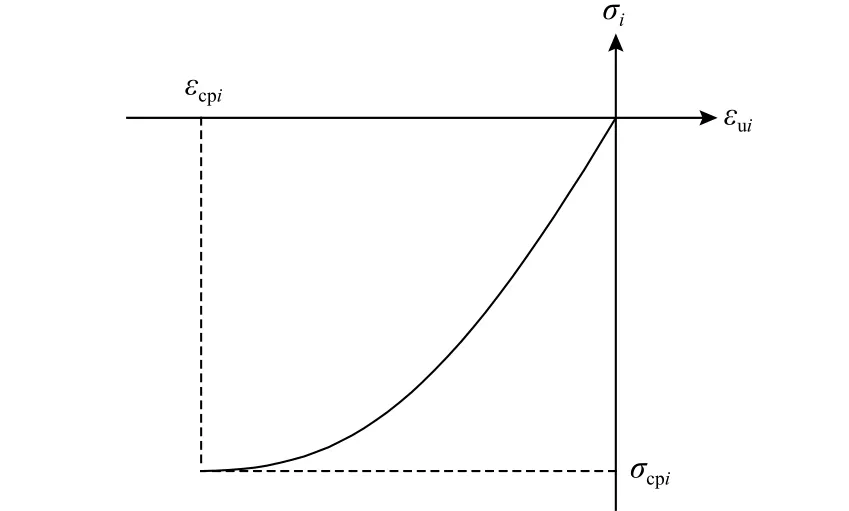
图2 ECC应力-等效单轴应变曲线示意图Fig.2 Illustration of stress-equivalent uniaxial strain curve of ECC

1.3 ECC双轴强度包络线

图3 ECC 双轴强度包络线示意图Fig.3 Illustration of biaxial strength envelope of ECC

为了展示在本文提出的双轴受压状态下的ECC本构模型(下文标记为“模型1”)中考虑双轴受压状态下ECC抗压强度变化的必要性，本文还建立了不考虑双轴受压状态下ECC抗压强度变化的本构模型(下文标记为“模型2”)，即模型2没有引入第1.3节中所述的理论，然后将模型1和模型2应用于不同配合比的ECC试件在不同应力比下的双轴受压有限元分析中，并对采用模型1和模型2进行数值计算得到的结果进行对比分析。

2 数值实现方法

本文分别推导了模型1和模型2的数值算法，并采用Fortran 语言编写了两个模型的用户自定义材料子程序UMAT以更新应力、1和2方向的弹性模量、剪切模量以及相关状态变量，将子程序嵌入ABAQUSv6.14中对ECC 双轴受压试验进行有限元分析。

模型1的数值算法流程如下所示(上标t表示当前增量步，t−1表示上一增量步)：

a)初始条件：

3 模型验证

本文通过对文献[33]中两种配合比的ECC试件在不同应力比下的双轴加载试验进行有限元分析验证模型1的有效性。

两种配合比的ECC 试件均由普通硅酸盐水泥、粉煤灰、精制石英砂、水、高效减水剂和PVA 纤维制作而成。ECC-I 试件的配合比为水泥∶粉煤灰∶石英砂∶水∶高效减水剂=1∶2∶0.6∶0.66∶0.024，纤维体积率为2.0%；ECC-II试件的配合比为水泥∶粉煤灰∶石英砂∶水∶高效减水剂=1∶3∶0.8∶0.92∶0.024，纤维体积率为2.0%。

通过单轴和双轴受压试验获得的材料属性见表1。本文假定ECC-I和ECC-II试件的等效泊松比为ν=0.2；模型参数l、m和n取自文献[35]，分别为−1.6、2.25和0.35。试件尺寸为100 mm×100 mm×100 mm，分别进行了应力比为0、0.25、0.5、0.75 和1时的双轴受压试验。

本文利用有限元程序ABAQUSv6.14进行数值分析，建立了图4所示的有限元模型分别进行ECC-I和ECC-II试件在上述五种应力比下的双轴受压分析。模型尺寸为100 mm×100 mm。在模型的左侧和下侧分别施加1、2方向的约束，在模型的右侧和上侧分别施加均布应力 σ1和 σ2，并令σ2/σ1=0、0.25、0.5、0.75和1以模拟ECC试件在五种应力比下的双轴受压试验。为了保证在各应力比下均能达到抗压强度，本文在ECC-I试件和ECC-II试件的1方向施加的初始荷载分别为75 MPa 和50 MPa，根据应力比可得2 方向上施加的初始荷载。如图4所示，为了考察不同网格划分方案对模型计算结果的影响，以ECC-I试件在单轴受压(β=0)和等压双轴受压(β=1)时为例，分别采用两种网格划分方案进行计算：图4(a)1×1网格和图4(b)5×5网格。有限单元类型采用线性减缩积分平面应力单元(CPS4R)。

表1 材料属性[33]Table 1 Material properties

图4 ECC试件双轴受压有限元模型Fig.4 Finite element model of ECCspecimens under biaxial compression

如图5所示为ECC-I试件在应力比β=0和β=1时分别采用1×1和5×5网格划分方案的主压应力方向的应力-应变曲线计算结果，可以看出在应力比β=0和β=1下，两种网格划分方案计算得到的主压应力方向的应力-应变曲线重叠在一起，并且在β=0时两种网格划分方案计算得到的极限抗压强度和极限抗压应变均一致，分别为−57.657 MPa和−0.298%；在β=1时也一致，分别为−66.527 MPa和−0.327%。由此可知，采用图4所示的不同网格划分方案并不影响数值计算结果。这是由于图4中的模型在两个方向上施加均布应力(σ1,σ2)的情况下，当采用1×1网格划分方案，即只有1个单元时，显然该单元的外力为(σ1,σ2)；当采用5×5网格划分方案时，根据静力平衡条件，每个单元的外力同样为(σ1,σ2)，因此可以得到相同的计算结果。为了节省数值计算时间，后文算例统一采用1×1的网格划分方案。

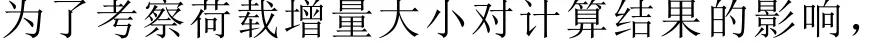
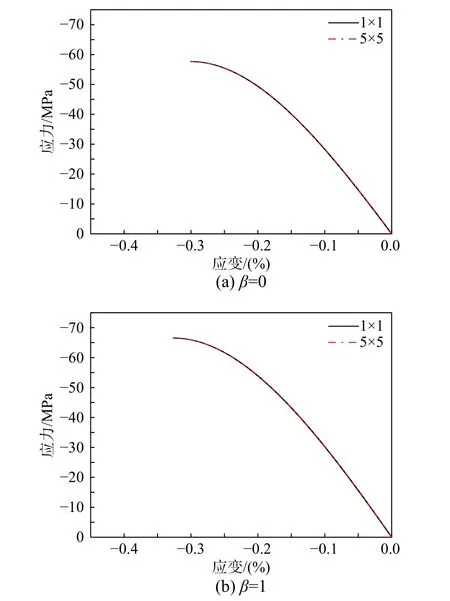
图5 应力比β=0和β=1的ECC-I 试件采用1×1和5×5网格划分方案的主压应力方向的预测应力-应变曲线Fig.5 Predicted stress-strain curvesof ECC-I specimens with stress ratios β=0 and β=1 in the major compressive stress direction with 1×1 and 5×5 meshing scheme

如图6所示为ECC-I试件在应力比β=0和β=1时分别采用三种最大时间增量步长计算得到的主压应力方向的预测应力应变曲线，表明所采用的三种最大时间增量步长均获得高度一致的计算结果。表2所示为ECC-I试件在应力比β=0和β=1时分别采用三种最大时间增量步长时的极限抗压强度和极限抗压应变计算结果，可知随着增量步长的减小，计算得到的极限抗压强度和极限抗压应变越接近于精确解。在应力比β=0和β=1时，采用2×10−4s 进行计算时得到的极限抗压强度和极限抗压应变与精确解的误差分别小于0.1%和1%。为了保证其余算例与精确解的误差也能在可接受的范围内，本文将最大时间增量步长统一设为1×10−4s。

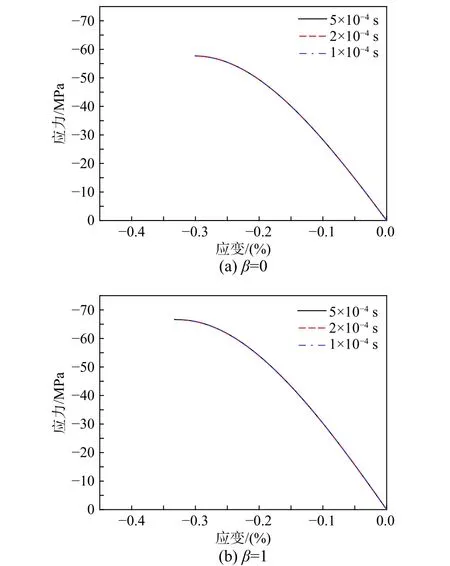
图6 应力比β=0和β=1的ECC-I 试件在不同最大时间增量步长下的主压应力方向的预测应力-应变曲线Fig.6 Predicted stress-strain curvesof ECC-I specimens with stress ratios β=0 and β=1 in the major compressive stress direction under variousmaximum time increments

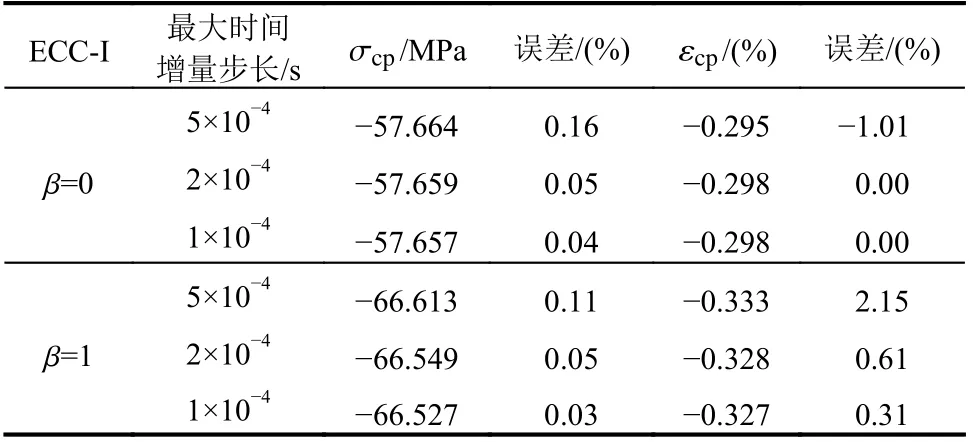
表2 应力比β=0和β=1的ECC-I 试件在不同最大时间增量步长下的主压应力方向预测极限抗压强度和极限抗压应变Table 2 Predicted ultimate compressive strengthsand ultimate compressive strains of ECC-I specimens with stress ratios β=0 and β=1 in the major compressive stress direction under variousmaximum time increments

图7和图8分别为ECC-I和ECC-II 试件在双轴受压时不同应力比β(β=σ2/σ1, σ1<σ2<0)下主压应力方向，即1方向的σ1−ε1曲线的试验和数值计算结果。

由图7和图8可知，在单轴受压(β=0)时，采用模型1和模型2分别进行有限元分析得到的两种ECC试件的σ1−ε1曲线与试验曲线吻合良好，且模型1和模型2的计算曲线重合。这是由于当试件处于单轴受压状态，模型1用双轴强度准则可确定σcp1=fc′p和εcp1=ε′cp，而模型2中令σcp1=fc′p和εcp1=ε′cp，因此每一增量步中模型1和模型2的E1相等，从而计算得到了重合的σ1−ε1曲线。

对于双轴受压(β≠0)的情况，采用模型1计算得到的σ1−ε1曲线与试验结果吻合良好，而采用模型2时则吻合程度较差。试验曲线和采用模型1进行有限元分析得到的σ1−ε1曲线都表现为在加载开始阶段，曲线的斜率变化幅度较小，近似为直线，随后越接近破坏点曲线的斜率下降越明显，到达破坏时曲线斜率为零。表明模型1 能够较准确地预测各双轴压应力比下ECC试件在主压应力方向加载过程中的刚度变化特征。而模型2在各双轴压应力比下的σ1−ε1曲线的初始斜率均相同，说明模型2无法准确预测ECC试件在不同双轴压应力状态下的刚度变化趋势。

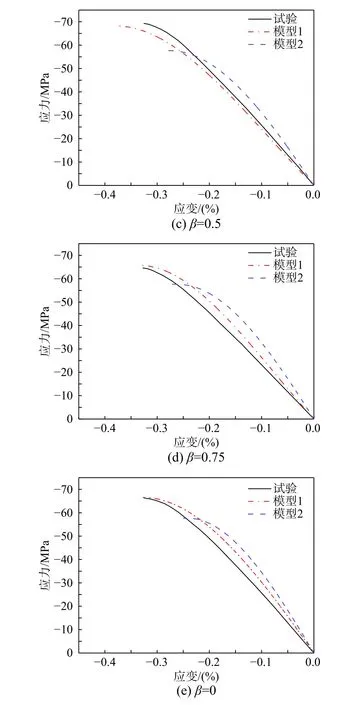
图7 各双轴压应力比下ECC-I 试件主压应力方向的应力-应变曲线Fig.7 Stress-strain curvesof ECC-I specimensin the major compressive stress direction under different biaxial stress ratios

表3为ECC-I和ECC-II试件在各应力比下主压应力方向的试验和预测极限抗压强度和极限抗压应变值。由表3可知模型1预测得到的ECC-I试件的极限抗压强度值与试验值相比，在β=1时最小，仅为0.03%，当β=0.25时的误差亦小于5%，模型1预测得到的ECC-II试件的极限抗压强度值与试验值相比，在β=1时误差最小为−0.00%，在β=0.5时最大，仅为−6.17%。表明模型1能够准确地预测双轴受压时ECC主压应力方向的抗压强度。

模型1预测得到的ECC-I和ECC-II试件在各应力比下的极限抗压应变也同样与试验结果较吻合，但预测到得到的ECC-I试件在β=0.25和0.5时和ECC-II试件在β=0.25时的误差分别达到了16.07%，15.34%和−14.89%，这是由于试验数据离散性较大而式(17)假定抗压强度σcpi与等效单轴抗压应变εcpi为线性关系，在上述三种情况下对应的抗压强度与等效单轴应变的坐标点刚好位于线性关系直线的两侧，故仅此三组有限元预测值与试验结果相差较大。

图8 各双轴压应力比下ECC-II 试件主压应力方向的应力-应变曲线Fig.8 Stress-strain curves of ECC-II specimens in the major compressive stress direction under different biaxial stress ratios

由表3可知模型2预测得到的ECC-I和ECCII试件在各应力比下主压应力方向极限抗压强度和极限抗压应变除了在单轴受压(β=0)时较准确，在双轴受压时皆与试验值相比相差巨大。表明模型2无法预测ECC抗压强度在双轴压应力状态下的变化。

从数值分析算例可知，模型1同时考虑了ECC在双轴受压时的非线性应力-应变关系和应力比的变化对抗压强度的影响，能更准确地描述不同配合比的ECC在不同应力比双轴受压状态下的力学行为。

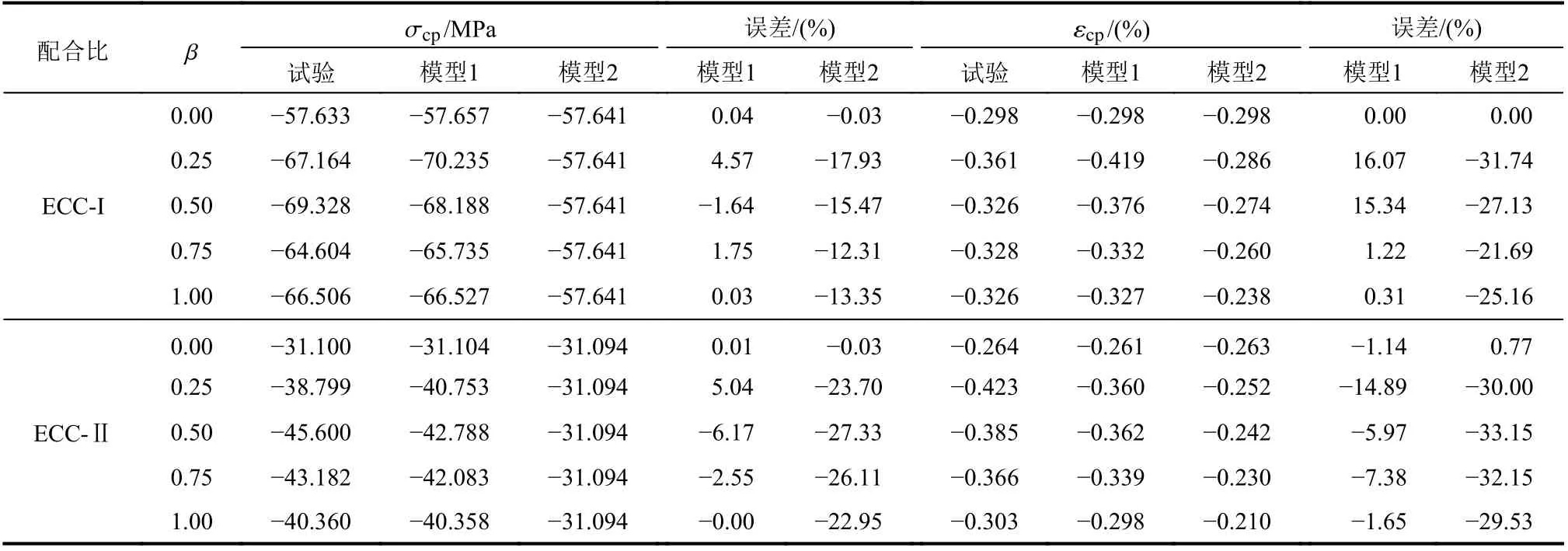
表3 各双轴压应力比下ECC-I 和ECC-II 试件主压应力方向的试验和预测极限抗压强度和极限抗压应变值Table 3 Experimental and predicted ultimatecompressive strengthsand ultimatecompressive strains of ECC-I and ECC-II specimensin the major compressivestress direction under various biaxial stress ratios

4 结论

(1)建立了一个能够同时考虑ECC在双轴受压时的非线性力学行为和抗压强度变化的二维本构模型，开发了本构模型的显式积分数值算法，采用Fortran 语言将模型算法编写成用户自定义材料子程序UMAT，并嵌入有限元分析软件ABAQUS v6.14中，用于预测ECC在双轴受压时的非线性力学行为及抗压强度变化。

(2)由数值计算结果可知，本文模型数值计算得到的两种不同配合比的ECC 试件在五组双轴压应力比下的应力-应变曲线与试验曲线吻合良好，并且能够较准确地预测各应力比下两种不同配合比的ECC试件在主压应力方向上的抗压强度和抗压应变，表明本文开发的ECC 本构模型能够较准确地预测不同配合比ECC试件在双轴受压状态下的力学行为。

(3)作为对比，建立了不考虑ECC在双轴受压状态下抗压强度变化的本构模型，并对上述两种不同配合比的ECC试件在五组应力比下进行数值分析，结果表明为了准确描述ECC双轴受压状态下的力学行为，有必要考虑其双轴受压状态下的抗压强度变化。本文提出的本构模型为准确预测ECC 在双轴受压状态下的非线性应力-应变关系和破坏强度提供了一种有效的分析方法。