简化三阶矩拟正态变换及其在结构可靠度分析中的应用

秦 琪，张玄一，卢朝辉，赵衍刚

(北京工业大学建筑工程学院，北京100024)

结构可靠度分析的一个核心问题是求解结构的失效概率和可靠指标。因随机变量常是多维的，失效概率的理论求解需要进行多重积分，计算难度极大往往无法实现。为提高可靠度分析的计算效率，前人发展了一系列结构可靠度近似分析方法并加以应用，如一阶可靠度分析方法(First order reliability method, FORM)[1−3]、二阶可靠度分析方法(Second order reliability method, SORM)[4−9]、蒙特卡洛分析方法(Monte Carlo Simulation, MCS)[10−14]和响应面法(Response surface method,RSM)[15−16]等。上述方法均需假设随机变量的联合概率分布或边缘概率分布及相关系数矩阵已知，从而基于Rosenblatt 变换[11]或Nataf 变换[12]将随机变量转换至相互独立的标准正态随机变量进行可靠度分析。由于实际工程中随机变量的统计数据往往不足以准确评估其概率分布，Rosenblatt 变换或Nataf变换不能有效进行，从而上述可靠度分析方法无法准确实现。

由于随机变量的前三阶中心矩含有大量统计信息，具有近似拟合随机变量概率分布的能力。因此，可以基于随机变量前三阶矩实现随机变量分布未知条件下的可靠度分析。该类方法大致包含了两种途径：第一种为基于随机变量的前三阶矩拟合其边缘概率分布[17−18]，并利用随机变量的相关系数矩阵进行Nataf 变换，从而实现随机变量分布未知条件下的可靠度分析；第二种方法为基于随机变量的前三阶矩和相关系数矩阵建立多项式拟正态变换模型[19−22]，实现随机变量的拟正态变换(包括正态变换和逆正态变换)，进而实现随机变量分布信息未知条件下的可靠性分析。由于第二种途径避免了对随机变量概率分布的拟合，相比第一种途径减少了分析步骤，计算相对简单。因此本文着重对第二种途径进行研究，其核心为基于随机变量前三阶矩的拟正态变换模型。

针对相互独立的随机变量，Zhao和Ono[19]提出了三阶矩多项式拟正态变换模型的准确表达式。虽然该模型具有显式解析表达式，但其系数的求解需要计算反三角函数，较为复杂，影响了其在实际工程中应用的效率。为考虑随机变量相关性的影响，Lu 等[22]提出了相关随机变量的三阶矩多项式拟正态变换模型，使用多项式模型实现了随机变量相关系数的转换。该模型具有明确的解析表达式，无需使用随机变量的边缘概率分布或联合概率分布即可实现任意相关随机变量与相互独立标准正态随机变量间的相互转换，具有广泛应用于实际工程的潜力。但由于三阶矩多项式变换模型本身求解的复杂性，Lu 模型在使用过程中不可避免的存在计算效率较低的问题。同时，Lu 模型未给出相关系数转换公式的适用范围，这给实际工程应用造成了一定的困难。

针对上述问题，本文首先基于Zhao-Ono模型发展了独立随机变量的简化三阶矩拟正态变换模型。根据简化模型，本文建立了相关随机变量的相关系数转换模型，并提出了相关系数转换模型的简明适用范围，从而实现了相关随机变量的三阶矩拟正态变换。随后，本文将提出的简化三阶矩拟正态变换模型与一阶可靠度分析方法(FORM)相结合，发展了随机变量分布未知条件下的可靠度分析方法，并分别采用独立随机变量和相关随机变量的数值算例对所发展的可靠度分析方法进行了验证。研究表明，本文提出的简化三阶矩拟正态变换模型具有较高的准确性和适用性，通过与一阶可靠度分析方法结合，能够实现在随机变量分布条件未知情况下的结构可靠度分析计算。

1 相互独立随机变量的简化三阶矩拟正态变换

1.1 三阶矩多项式拟正态变换准确模型

1.2 简化三阶矩多项式拟正态变换模型

将式(6)代入式(3)，由反正切函数的值域|θi|≤π/2，假定反余弦函数只取单值，则其值域为[0,π/2)，同时考虑到同一个变量的反正弦函数arcsin(·)与反余弦函数arccos(·)之和为π/2，可得到α3i的连续函数如下：

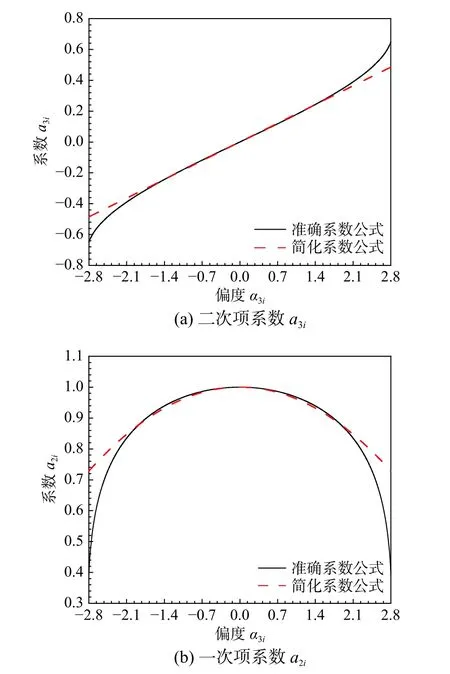
图1 简化公式与准确值对比示意图Fig.1 Comparison of the exact and simplified coefficients

观察图1和图2可知：

1)当−2≤α3i≤2时，本文提出的简化公式计算结果与准确值基本吻合。对于α3i的取值范围大致在−2到2之间的实际工程[23]，可以认为简化公式具有较高的准确性。

2)系数a2i简化公式的误差变化趋势与系数a3i简化公式的误差变化趋势相反，且a3i的误差值比a2i的误差值大。当−2≤α3i≤2时，简化公式得到的a2i和a3i与准确值之间的相对误差分别在0.8%和5%之内，均满足实际工程准确性的容差要求。

将简化公式代回式(1)和式(2)中，可得到三阶矩拟正态变换简化模型定义如下：

图2 简化公式系数与准确值间的相对误差Fig.2 Relative error between simplified and exact coefficients

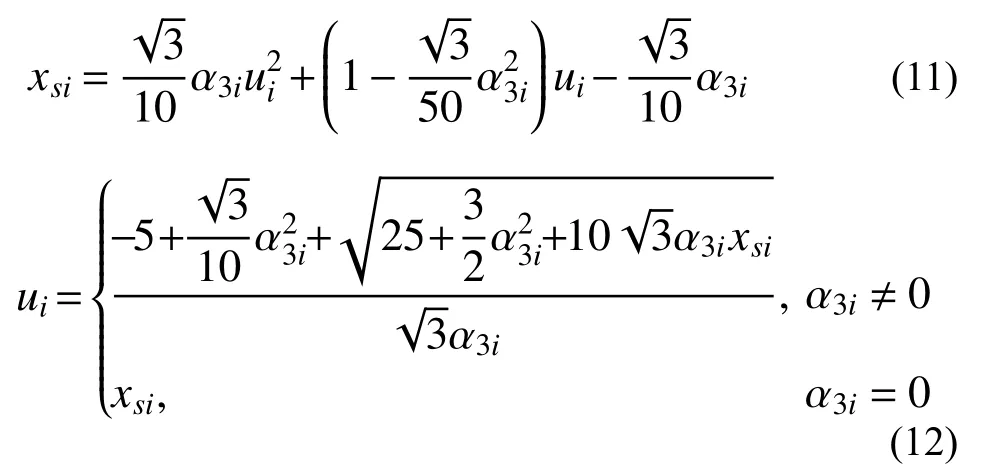
可以看出，简化后的三阶矩多项式拟正态分布系数公式去掉了三角函数与反三角函数，将系数a3i、a2i分别以随机变量偏度α3i的一元线性方程和一元平方方程来替代计算，如此既简化了计算过程又统一了公式中的变量，可以直接明了地表现出随机变量的概率特征及系数结果随特征值的变化情况。

2 相关随机变量的三阶矩多项式拟正态变换

2.1 三阶矩多项式拟正态变换准确模型

当随机变量X的相关性不可忽略时，通过三

式中，L0为对Z的相关系数矩阵R Z进行Cholesky分解后得到的下三角矩阵。基于随机变量前三阶矩得到的R Z有可能出现非正定的情况。为了解决这一问题，Ji等[24]提出了一种使用较小的正值(如0.001)代替R Z原对角特征矩阵中负值的近似分析方法。

将式(15)代入式(13)和式(14)可得相关随机变量X的拟正态变换模型：

根据式(3)和式(5)可知，a3i和a3j的准确求解需要进行三角函数运算，因此ρij和ρ0ij间转换关系的确定需进行较复杂的计算。同时，式(18)～式(20)的适用范围尚未明确，这给三阶矩多项式拟正态变换模型在实际工程计算中的应用造成了一定程度的影响。

2.2 简化三阶矩多项式拟正态变换模型

为简化相关随机变量的三阶矩拟正态变换计算过程，本文首先将提出的简化系数(式(8)和式(9))代入2.1节的准确公式中得到：

对任意随机变量和相关标准正态随机变量的相关系数间的转换公式进行化简。结果如下：

将式(23)～式(25)与式(15)～式(17)联立，即为相关随机变量的简化三阶矩拟正态变换模型。式(23)～式(25)将ρij和ρ0ij间的转换公式定义为与偏度相关的简单运算公式。与需要进行三角函数运算的理论公式相比降低了计算难度，从而提高了运算效率，使三阶矩拟正态变换更适用于实际工程。

为提出相关系数转换公式的适用范围，下面对式(23)～式(25)进行深入探讨。观察式(24)可知，由ρij向ρ0ij进行转换存在一定的前提条件。同时考虑到相关系数的定义，ρ0ij应满足−1≤ρ0ij≤1和ρij·ρ0ij≥0。故可解得ρij的简明取值范围如表1所示。通过表1，可以对相关系数转换公式适用范围进行确定，从而直接判断三阶矩拟正态变换模型是否适用于某工程实际问题。

3 基于简化三阶矩多项式拟正态变换模型的一阶可靠度分析方法

对于随机变量分布已知的情况，一阶结构可靠度分析方法(FORM)[1]具有计算简单适用范围较广等优点，广泛应用于实际工程的可靠度分析中。该方法采用一维线性函数对结构的功能函数进行模拟，将结构的可靠指标定义为标准正态空间内原点到极限状态平面的最短距离。分析过程中，常规FORM需要基于随机变量的分布使用Rosenblatt 变换或Nataf 变换将任意空间中的随机变量转换至标准正态空间。

对于随机变量分布未知的情况，可以基于随机变量的前三阶矩使用简化三阶矩拟正态变换模型进行随机变量的正态及逆正态变换。从而实现随机变量分布未知条件下的FORM分析。基于简化三阶矩逆正态变换模型的FORM 流程如下：

1)首先获得原始变量X前三阶矩与相关系数；

2)将X划分为分布已知的随机变量X1和分布未知的随机变量X2，分别采用Rosenblatt/Nataf 变换和简化三阶矩多项式拟正态变换模型对X1和X2进行正态变换，将任意随机变量X表示的功能函数G(X)转化为独立标准正态随机变量表示的g(U)；

表1 简化三阶矩拟正态变换中ρ0ij 的表达式及其适用范围Table 1 Expressionsand applicable rangesof ρ0ij in the simplified TMNT

3)定义初始可靠度指标β0=0和初始验算点U0=[0,0,···,0]；

4)计算U0处功能函数g(U)对U的导数；

5)计算灵敏度系数αi，

8)将新的可靠指标β 和新验算点U1代回步骤3)，重复步骤3)～步骤8)，直至|β−β0|≤容许误差，β 即为所求得的可靠指标。

综上所述，基于简化三阶矩拟正态变换模型的FORM分析流程与随机变量分布已知条件下的FORM 流程一致，仅在进行变量正态变换的时候与常规FORM采用的模型不同。因此，基于简化三阶矩拟正态变换的FORM无需额外的计算步骤，确保了可靠度分析的高效性。

4 结构可靠度分析算例

4.1 随机变量相互独立条件下可靠度分析算例：屋顶结构可靠度

为验证本文提出方法的准确性和适用性，本算例对一跨长为l，受均布垂直荷载为qr的屋顶结构进行可靠度分析。本算例中屋顶结构的受力图和计算简图分别如图3(a)和图3(b)所示。该结构的顶弦和压杆材料为混凝土，弹性模量为Ec，横截面面积为Ac。底部绳索和拉杆材料为钢材，弹性模量为Es，横截面面积为As。在屋顶结构计算分析中，均布垂直荷载qr近似简化为三个节点集中荷载P=qrl/4。结构的使用极限状态设定为结构最大竖向位移等于容许竖向位移ua的情况，相应功能函数为[25−27]：

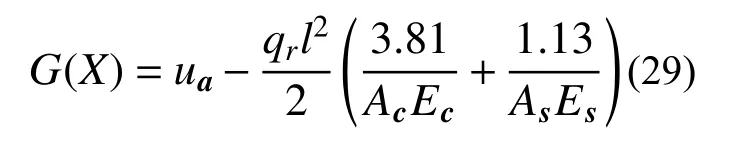
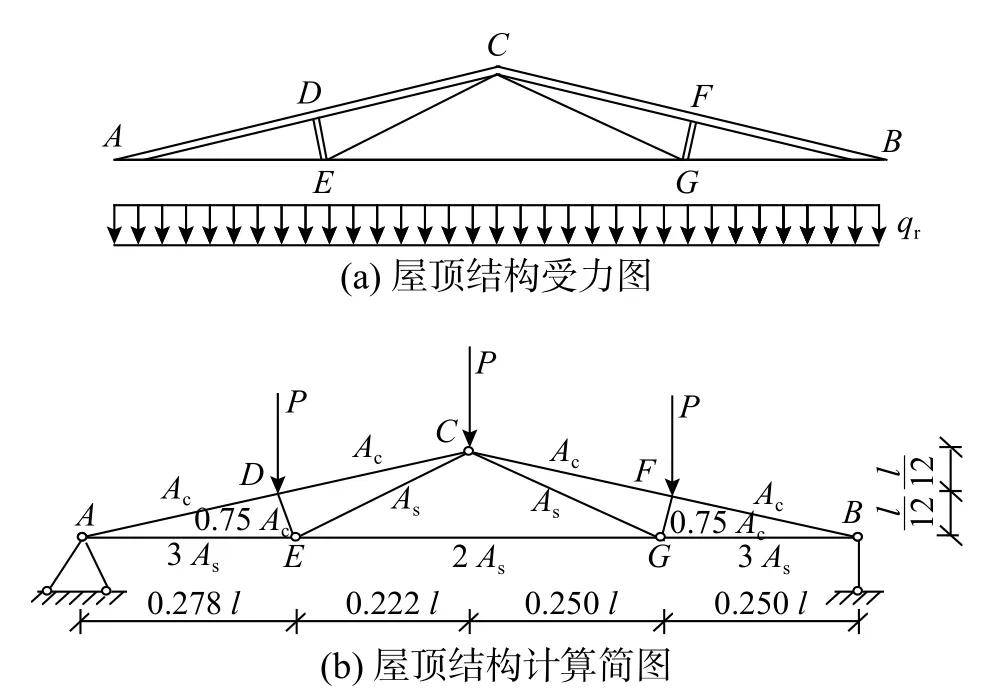
图3 屋顶结构示意图Fig.3 Schematic diagram of the roof structure

本算例中随机变量的统计信息如表2所示，假设各变量间相互独立。为验证基于简化三阶矩多项式拟正态变换模型的FORM的准确性和适用性，本算例分别使用基于三阶矩拟正态变换简化模型和准确模型的FORM法、基于随机变量分布信息的FORM法和MCS法对比研究。

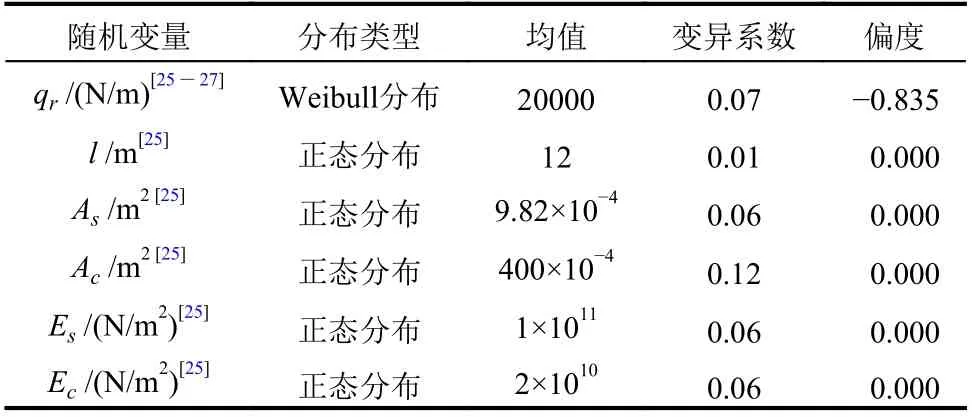
表2 算例1的随机变量分布及前三阶矩Table 2 Distributionsand first three momentsof random variablesfor example 1

图4 随机变量相互独立条件下β 随ua 变化示意图Fig.4 Changesof β with ua considering independent random variables

使用不同方法得到可靠度指标β 随容许竖向位移ua的变化规律如图4所示。其中，细实线、粗虚线以及点划线分别表示基于三阶矩拟正态变换准确模型、三阶矩拟正态变换简化模型、以及基于随机变量分布信息的FORM 得到的可靠指标，圆圈符号为MCS法计算得到的可靠指标。

由图4可知，随着容许竖向位移的增加，结构的可靠度指标有明显的上升趋势。在本算例考虑的允许位取值范围内，简化三阶矩多项式拟正态分布与MCS法和基于随机变量分布信息的FORM法误差满足工程容许值5%。从而证明了本文提出的简化三阶矩拟正态变换在随机变量相互独立条件下的准确性和适用性。

4.2 考虑随机变量相关性的可靠度分析算例：CRTSII 型板式无砟轨道可靠度

为进一步分析简化三阶矩拟正态变换模型在随机变量相关性不可忽略条件下的准确性和适用性，本算例拟采用该方法对高速铁路CRTSII型板式无砟轨道结构的可靠度进行分析。

连续铺设的桥梁地段CRTSII型板式无砟轨道结构，其钢筋混凝土结构在服役期间达到一定的温度条件后，会产生巨大的温差压力，这种由轨道板整体温度升高引起的压力极易造成轨道板与砂浆层的剥离，因此需要对其稳定性进行评估[28]。假设CRTSII型轨道板与CA 砂浆层因为升温导致完全剥离，轨道板失稳的功能函数近似表示为[29− 31]：

式中：λCA为临界失稳压力提高系数，表征CA 砂浆层粘结力对轨道板位移的限制作用；λcr为考虑了轨道板初始偏心等各不利条件引入的折减系数；Ftk为由轴向温度作用产生的应力标准值。临界压力Pcr[31]和轴向温度作用Ftk[28]计算公式分别为：

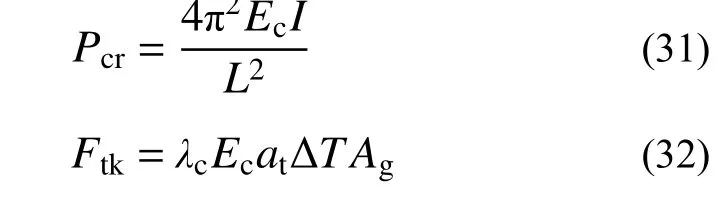
式中：ΔT为轴向温度；Ec为轨道板弹性模量取为35.5 GPa；I为轨道板惯性矩取0.0017 m4；L为计算长度取我国高铁桥梁常用箱梁长32 m；λc为轨道板弹性模量折减系数，一般取0.3～0.6，本例取0.4，线膨胀系数at=10−5℃−1，轨道板截面积Ag=0.51 m2。

本算例将参数λCA、λcr、ΔT看作随机变量。由于统计数据的缺乏，上述随机变量的统计信息暂时无法准确确定。为了对本文提出方法进行验证，假设上述随机变量的分布及相关性已知，相应的统计特征值和两两之间的相关系数分别假定为表3和表4所示的数值。因为随机变量的分布信息已知，因此可以采用常规FORM 对CRTS II型无砟轨道板的纵向失稳可靠度进行分析。

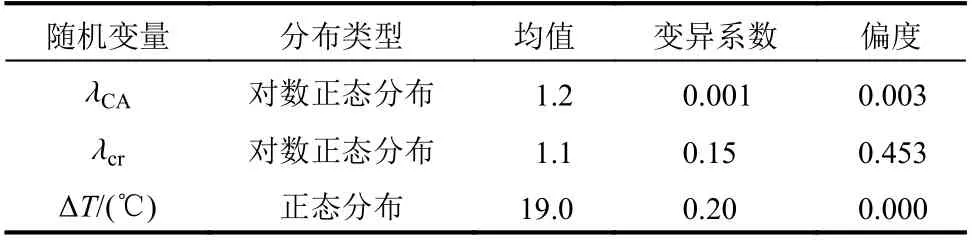
表3 算例2的随机变量分布及前三阶矩Table 3 Distributions and first three moments of random variablesfor example2

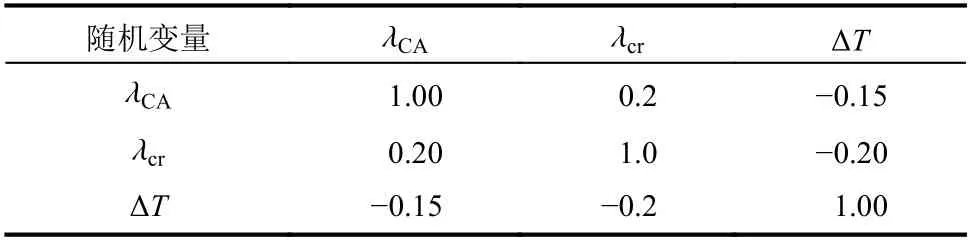
表4 算例2的随机变量间相关系数Table 4 Correlation coefficients between different random variables for example 2

本算例使用提出的可靠度分析方法对轨道板的纵向失稳可靠度进行了分析。并将得到的结果与基于三阶矩多项式拟正态变换准确模型的FORM 法、常规FORM法和MCS法得到的结果进行对比。

考虑随机变量相互独立，使用不同方法得到β 随轴向温度ΔT均值µΔT、变异系数COVΔT和折减系数偏度α3λcr的变化趋势如图5～图7所示。考虑随机变量相关，使用不同方法得到β 随相关系数变化如图8～图9所示。其中，ρ12、ρ13和ρ23分别表示λCA与λcr、λCA与ΔT以及λcr与ΔT两两间的相关系数。图8为单一相关系数的影响趋势，考虑某一特定相关系数时其余值取固定值如表4所示。图9为CRTSII无砟轨道板纵向失稳可靠度随ρ13和ρ23变化的三维示意图。

由图5～图9可以看出：

1)对于所有情况，三阶矩多项式拟正态变换简化公式与准确公式的计算结果基本一致。通过计算，相对误差值普遍小于1%。这表明简化公式具有较高的准确性。

2)针对大多数情况，使用三阶矩多项式拟正态变换与FORM结合得到的结果与基于分布的MCS及FORM 得到的结果高度吻合。但对于COVΔT较小、α3λcr>1.05以及ρ23较小的情况，基于随机变量前三阶矩得到的可靠指标与基于随机变量分布的MCS和FORM分析结果存在一定的误差。前两者可能是因为随机变量的非高斯性较强，前三阶矩无法准确描述功能函数的统计特征，三阶矩多项式拟正态变换模型存在一定误差。此时，可以使用基于随机变量前四阶矩的可靠度分析方法[25]提高计算精度。后者则可能因为使用Cholesky分解时存在负正定情况，直接替换会造成三阶矩多项式拟正态变换模型存在误差，计算可知，误差值在容许范围内。

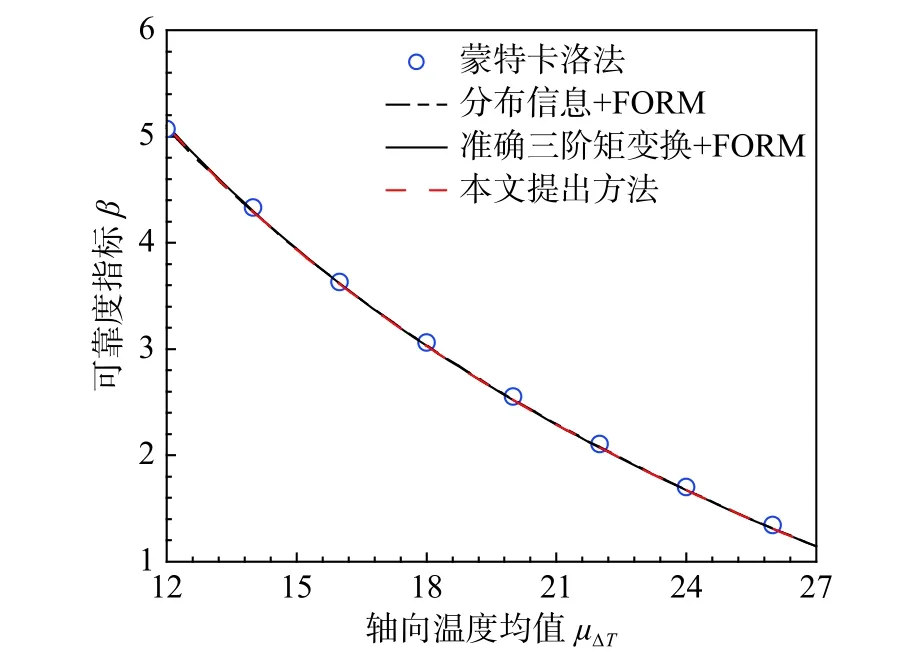
图5 随机变量相互独立条件下β 随µΔT 变化示意图Fig.5 Changes of β with µΔT considering independent random variables

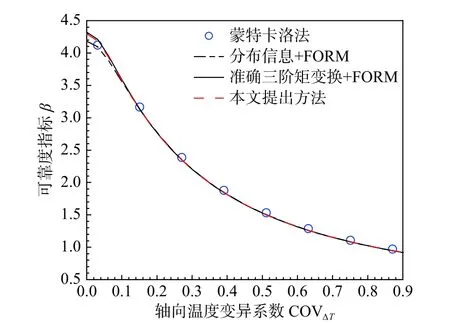
图6 随机变量相互独立条件下β 随COVΔT 变化示意图Fig.6 Changesof β with COVΔT considering independent random variables

图7 随机变量相互独立条件下β 随α3λcr 变化示意图Fig.7 Changesof β with α3λcr considering independent random variables

图8 β 随单一相关系数变化示意图Fig.8 Changes of β with one correlation coefficient

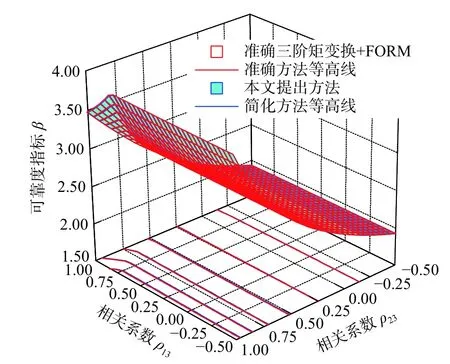
图9 β 随ρ12和ρ23变化三维示意图Fig.9 Changesof β with ρ12 and ρ23

3)CRTSII型无砟轨道板可靠指标均随变量的均值、变异系数和偏度增大而减小。这是因为当均值、变异系数和偏度升高时，功能函数的变异性增大，从而导致轨道板的可靠性降低。

4)当相关系数较小时，CRTSII型无砟轨道板的纵向失稳可靠指标随ρ12和ρ13的增加缓慢增大；当ρ13取值较大(ρ13>0.85)时轨道板可靠指标随ρ13表现出轻微的下降趋势。对于ρ23的所有取值，CRTSII 型无砟轨道板的纵向失稳可靠指标随ρ23上升均呈现出明显的下降趋势。这表明λCA与λcr、λCA与ΔT间的相关性对轨道板的可靠性影响不大，而λcr与ΔT间的相关性越强轨道板的可靠性越弱。

5 结论

针对现有三阶矩拟正态变换模型较为复杂且适用范围不明确的问题，本文发展了独立及相关随机变量的简化三阶矩拟正态变换模型，并提出了相关系数转换模型的简明适用范围。随后，通过与FORM分析方法结合，发展了随机变量分布未知条件下的可靠度分析方法。研究表明：

(1)提出的简化三阶矩多项式拟正态变换模型具有简明的表达式，在实际工程中常见的偏度范围内与准确模型结果吻合，具有较高的准确性。

(2)提出的简化三阶矩多项式拟正态变换模型适用范围具有简明的显式表达，简明扼要地划定了简化三阶矩拟正态变换的适用范围，便于实际工程应用。

(3)提出的可靠度分析方法可用于随机变量分布未知条件下的可靠度分析，在本文的数值算例和CRTSII 型轨道板算例中均表现出较高的准确性和高效性。