基于数字图像相关技术测量刨花板材料力学参数

陈 州，杜新喜，张 慎，袁焕鑫

(1.中南建筑设计院股份有限公司，武汉430071；2.武汉大学土木建筑工程学院，武汉430072)

国标《刨花板》(GB/T 4897−2015)[1]给出了刨花板的准确定义：“将木材或非木材植物纤维原料加工成刨花(或碎料)，施加胶粘剂(和其他添加剂)，组坯成型并经热压而成的一类人造板材”。按使用用途可分为：普通型刨花板、家具型刨花板、承载型刨花板及重载型刨花板。根据刨花板不同的组成结构，又存在单层结构刨花板、三层(包括多层)结构刨花板、渐变结构刨花板、定向刨花板、华夫刨花板、模压刨花板等多种形式。本文研究对象选取的是如图1所示的市面上常见的三层结构“P2 型干燥状态下使用的家具型刨花板”。

图1 三层结构刨花板(已切割成梁样品用于弯曲试验)Fig.1 Three-layer conformation of particleboard (cut into beam specimens for bending test)

我国的刨花板生产始于20世纪50年代后期，经历了由80年代的上升，到90年代由于质量差、规模小、技术设备落后等原因而发展缓慢甚至被市场抛弃。直到本世纪初，在引进了国外先进生产线及提高工艺水平后，我国的刨花板产品质量显著提高，又重新回归市场。近年来，需求量逐年上升加之国家优惠政策的出台，为我国刨花板乃至整个木材行业的发展创造了极好的条件[2]。

目前国内外对刨花板力学性能研究及材料参数测量尚无统一的试验方法与标准。欧美等发达国家对刨花板进行了大量研究，并广泛采取了一批新技术与新方法。Moarcas和Irle[3]利用自制可拆卸式应变计，通过四点弯曲试验测量了P5型刨花板(BS EN 312-5)的泊松比。Wilczyński 和Kociszewski[4]对从刨花板上剥离的各结构层(面层和芯层)材料试件进行了压缩试验，并利用电阻应变片测量了样品的弹性应变，各结构层被当作是正交各向异性材料建模，随后分别测算了各层材料相应的12个弹性参数的平均值。国内学者针对刨花板力学性质的研究尚处于起步阶段，均普遍采用国标《人造板及饰面人造板理化性能试验方法》(GB/T 17657−2013)[5]4.7节中给出的测量方法，局限于对刨花板材料静曲强度和弹性模量的测定。

本文结合近年来数码摄像技术及相应图像算法的改进与飞速发展，采用国标[5]中规定的三点弯曲试验，通过对样品变形前后数字图像分析，来获取刨花板材料力学参数，为今后刨花板力学性能的研究及相关规范的完善提供参考依据。

1 试验概况

1.1 刨花板材料本构模型

国外学者普遍采用正交各向异性本构关系对刨花板力学行为建模[4,6 −7]。由于刨花板材料特殊的物理构造：内部为交叉错落结构的颗粒状，结构均匀，各部方向的性能基本相同。本文采取了“横观各向同性”本构关系用于模拟三层结构(三明治式，见图1)刨花板的力学性能。在工程常用材料各本构模型中，横观各向同性适合于层状介质的宏观建模，其特点是平行于各向同性面(横向)材料都具有相同的弹性性质。根据Wilczyński和Kociszewski[4]公布的试验数据，可见刨花板各结构层在各向同性平面内材料各方向弹性参数大致相同，而垂直此面方向的值不同。由此验证了使用横观各向同性本构关系对刨花板材料力学行为建模的可行性。

如图2，取各向异性方向对应于各向同性面的法线方向(z，1，L方向)，T平面(或xy平面，或23平面)为各向同性平面。板理论中，通常将板厚方向标记为1或z，故本文采用了如式(1)的标注方式：

用于表示定义板局部坐标系的3个坐标轴方向。在弹性阶段，刨花板材料应力-应变关系，即横观各向同性本构方程[8]由广义胡克定律给出：

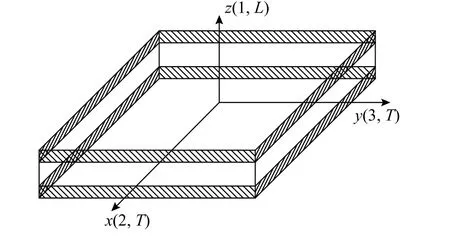
图2 刨花板几何模型Fig.2 Geometric model of particleboard

1.2 三点弯曲力学试验

试验开始前，待测刨花板被切割成27个尺寸为h×b×L=15 mm×50 mm×260 mm 的梁样品(图1和图3(a))，并储存在恒温恒湿(温度20±2℃，相对湿度65±5%)环境中。通常需要在试件表面制作人工散斑，其主要原因是为了在试验后期对所采集样品的数字图像进行分析时能取得较高的测量精度，且喷涂的散斑点越随机，该测量方法越精确。由图1可见，刨花板材料天生的自然纹理分布就具有很强的随机性，其表面本身就可以作为自然散斑图，因而省略了试验前期人工喷涂散斑点的准备工序。

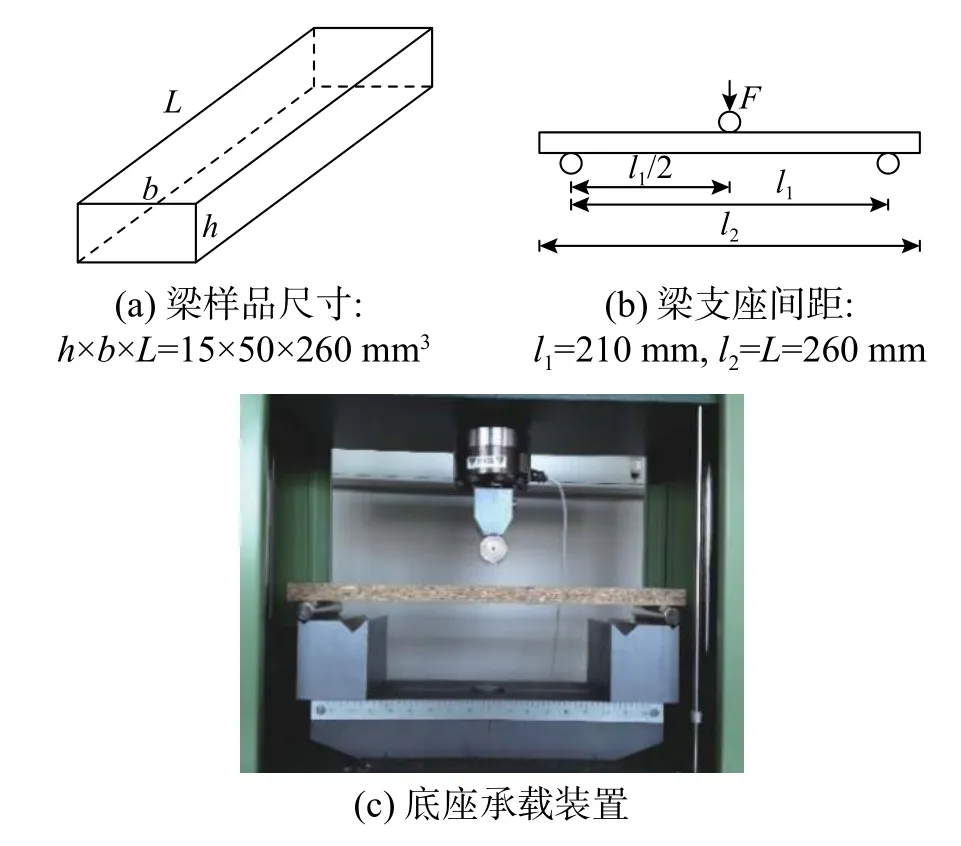
图3 试验样品及支座尺寸Fig.3 Sampleand support sizefor testing

试验时，梁样品试件被水平放置于底部间距可调节的圆柱形支座平台上，底座承载装置见图3(c)。梁支座距离为14倍梁高l1=14h(图3(b))。

试验过程中使用了计算机数控式万能材料试验机DELTALAB EM 550进行加载，及德国产Allied Vision Mako工业相机对梁样品感兴趣区域(Region Of Interest，ROI)进行图像拍摄。该材料试验机与安装有相关专业软件的计算机相连接，可实现伺服控制，数据采集与分析。相机正对于样品ROI，且使用了人工照明设施，以保证所获得的照片图像的质量。试验装置及过程如图4。

图4 三点弯曲试验装置Fig.4 Three-point bending test device

为了减小试验期间在荷载及支座附近局部效应的影响，每个样品试件所选择的ROI(见图5)仅覆盖梁表面左侧局部部分距支座及荷载施加点20 mm 处。试验时，加载速度设定为0.05 mm/s，采用单调分级从零(荷载增量30 N)加载直至试件破坏，每级荷载施加完毕机器停留30 s以获取图像。每个样品拍摄了11张图片(第一张为未加载时初始状态下的参考图片)，对应于施加荷载为0 N～300 N。

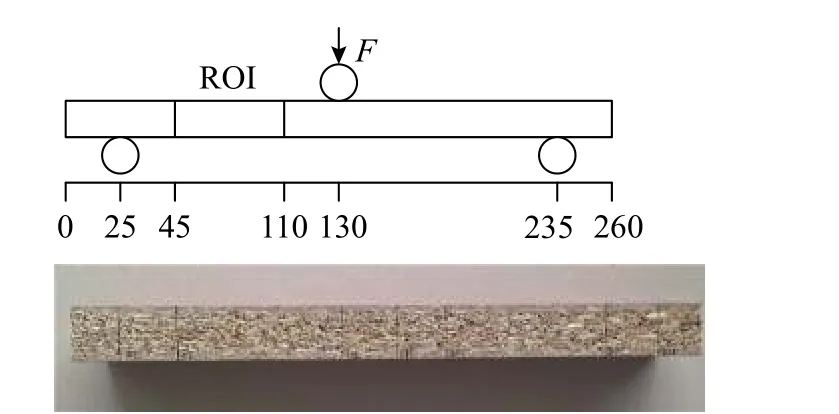
图5 ROI所在梁试件的位置/mm Fig.5 Location of the ROI

图6展示了在同一试验装置(图4)下所有27个样品三点弯曲试验过程中获得的荷载-位移曲线。值得注意的是，由于刨花板材料微观结构的异质性，全部样品的荷载-位移曲线的总体可变性相对较高，且300 N 在弹性范围之内。

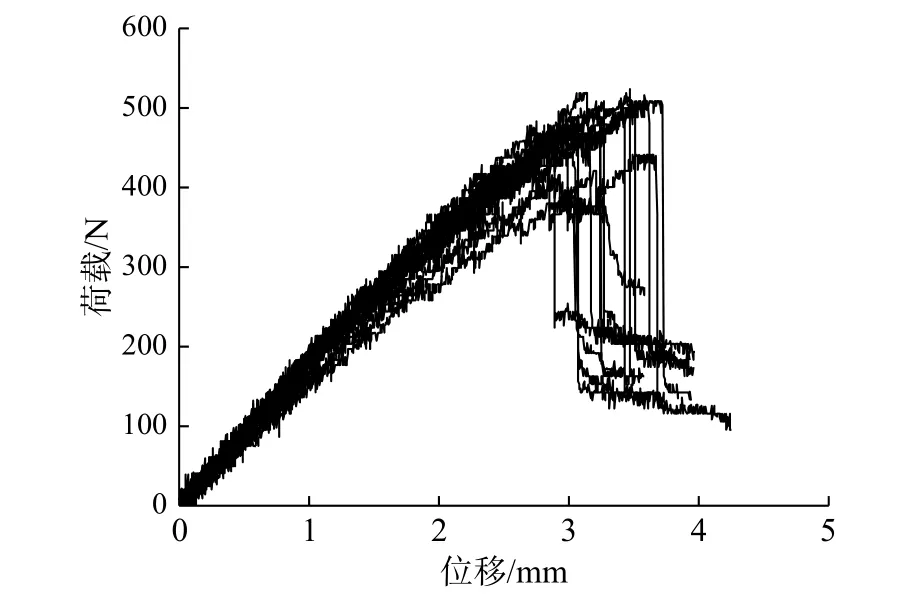
图6 全部样品跨中荷载-位移曲线Fig.6 Load-deflection curvesat mid span

2 材料参数测量方法

2.1 数字图像相关技术

数字图像相关(Digital Image Correlation，DIC)技术，作为一种简单、实用、高效的非接触式全场位移、应变测量方法，目前应用于多个专业领域。其基本原理是通过追踪两张散斑图像中某点在物体表面变形前后的位置从而获取该点的位移向量。本小节通过使用基于MATLAB软件开发平台自主编写的三节点三角形网格化DIC(T3-DIC)程序，对物体在加载的各个阶段所获得的数字照片进行分析，从而实现了对ROI 位移场的测量。不同于传统的子区DIC方法，T3-DIC是基于有限元网格位移表征的DIC技术。限于篇幅限制，对DIC基本原理的阐述并非本文重点内容，本小节只给出了T3-DIC对代表性样品ROI网格节点位移场的测量结果。事实上，从提出到现在三十余年，世界各国科研工作者及工程技术人员对该方法做了大量的研究工作[9−10]，在力学诸多领域取得了重大成果。

对每个样品，通过将第n(n=2,3,···,11)张图像与初始图像(即第1张图像，被视为处于未加载状态的参考图像，如图7(a))相关联，可以计算出图像n中ROI网格节点位移场。图7(b)为一代表性样品ROI的初始(红)网格及经T3-DIC测算后的变形(黑)网格。由于该样品ROI的物理几何尺寸(单位为mm)及像素坐标(单位为pix)均为已知量，经换算，一个单位像素的物理尺寸为52.2µm。三角形单元大小选择为大约16个像素(即0.835 mm)。ROI位移场的测量值记为uexp，其水平分量u及垂直分量v在初始图像像素坐标中的分布见图7(c)及图7(d)。从中可以看出：水平分量u根据两个坐标y和z变化，而垂直分量v几乎仅取决于横坐标y。

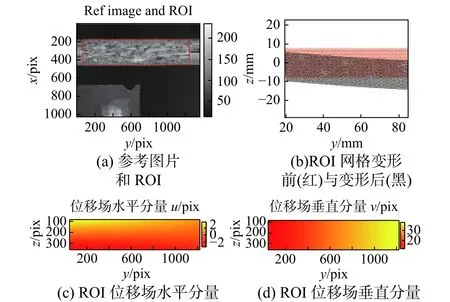
图7 利用DIC技术测量代表性样品位移场Fig.7 Measurement of the displacement field for a representativesample by DICtechnology

2.2 铁木辛柯梁弯曲问题解析解

铁木辛柯梁是经典梁理论考虑横向剪切变形后的修正梁理论。Murata 和Kanazawa[11]对云杉和水曲柳木材梁试件进行了三点弯曲试验，用图像分析法测量了弯曲梁的挠度曲线，并基于铁木辛柯梁理论用多项式回归分析法计算了木材的弹性模量和剪切模量。

如图8(a)所示，长度为L的等直梁中部(y=L/2)受大小为F的横向力。根据材料力学[12]基本理论，在横坐标y处、对x轴惯性矩为Ix的截面，其正应力σyy取决于绕x轴的弯矩Mfx，并在该截面纵坐标为z的任意点处大小为：

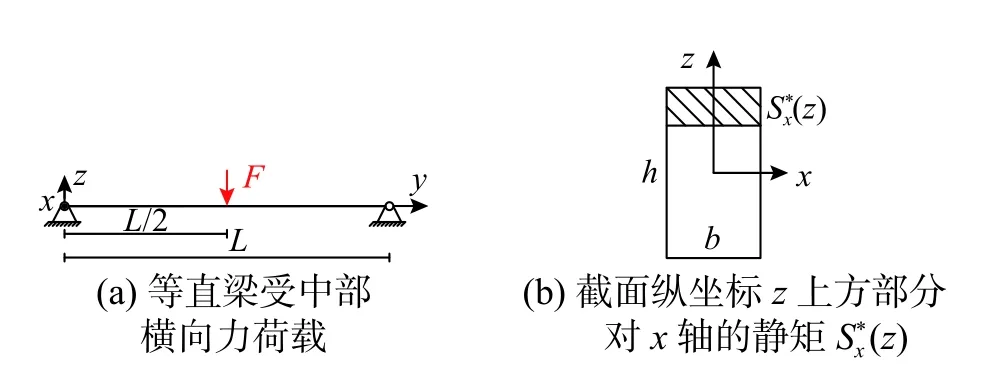
图8 铁木辛柯梁三点弯曲模型Fig.8 Model of Timoshenko beam under three-point bending

由于本文采用的是2维DIC技术，只能获得观察平面内的位移场，故将该空间问题简化为弹性力学的平面应力问题，在平面应力状态下有：

梁试件在截面高度h方向尺寸远小于宽度b及长度L方向，相比于其他应力分量，横向正应力σzz为极小量可忽略不计(σzz≈0)，则前述应力-应变关系(式(7))可表示为：

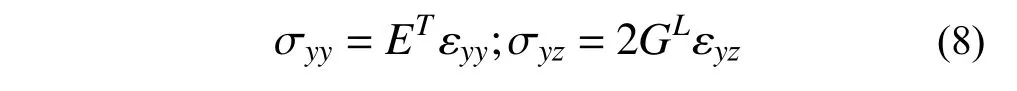
如图9，水平位移分量(沿y轴)及垂直位移分量(沿z轴)分别记为u和v，基于小变形假设，将式(3)和式(4)代入式(8)可得以下微分方程：

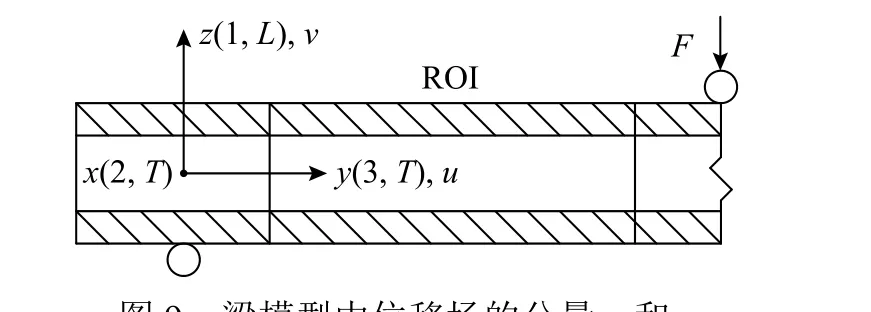
图9 梁模型中位移场的分量u 和vFig.9 Components u and v of the displacement field of the beam model

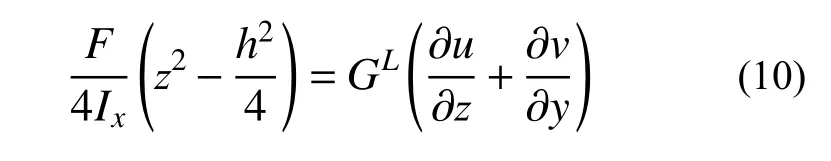
求解上述微分方程式(9)与式(10)则位移分量u和v应具有如下形式：

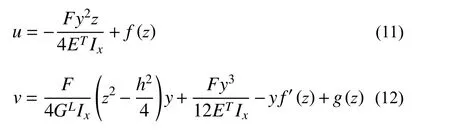
式中，f和g均为仅取决于z的可微分函数。

类似于横向正应力σzz，横向正应变也是相较于其他应变分量的极小量，故可忽略不计(εzz≈0)：

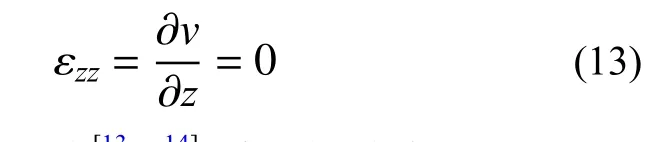
这与经典板理论[13−14]采取的基本假设相同，实际上本试验中使用的梁尺寸h＜b＜L，故引入板理论知识对应力、应变进行分析计算是合理的。由式(12)与式(13)可得：

2.3 有限元模型修正方法

对于给定的荷载条件、几何形状及材料特性，有限元法提供了位移场的数值解。同时，该方法还可以用作数值工具来反向地解决从位移场中识别材料参数的问题，这便是有限元模型修正(Finite Element Model Updating，FEMU)方法的基本原理。

在有限元方法中，通常选择多项式函数作为单元位移插值函数，并利用节点处位移连续性条件，将位移插值函数表示为形函数矩阵N与单元节点位移列阵Ue的乘积形式。如图10，三角形单元Ωe节点i，j，k的坐标分别为(yi,zi)，(yj,zj)，(yk,zk)，节点位移分别为(ui,vi)，(uj,vj)，(uk,vk)，则：

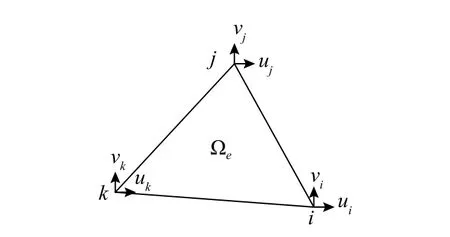
图10 三节点三角形单元Fig.10 Three-nodetriangular element

各形函数Ni(yi,zi)(下标i，j，k轮换)应满足以下性质：在单元相关节点处形函数的值为1，不相关节点处值为0；在单元任一点上三个形函数和为1。基于小变形假设应变-位移关系，由式(18)可推导出ROI内应变场为：

对于该三节点三角形单元，考虑到简单性、完备性、连续性及待定系数的唯一确定性原则，分别选取单元中各方向位移模式：

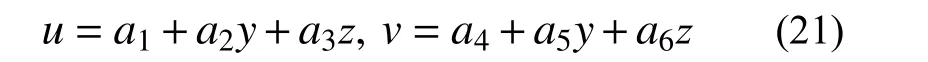
将3个节点坐标和位移分量代入式(21)可得a1,a2,···,a6六个待定系数。各形函数Ni(yi,zi)(下标i，j，k轮换)及几何函数矩阵B的推导为经典有限元理论基础知识，在此不再赘述,可参阅文献[15]。由式(7)可得平面应力状态下的柔度矩阵S表达式为：

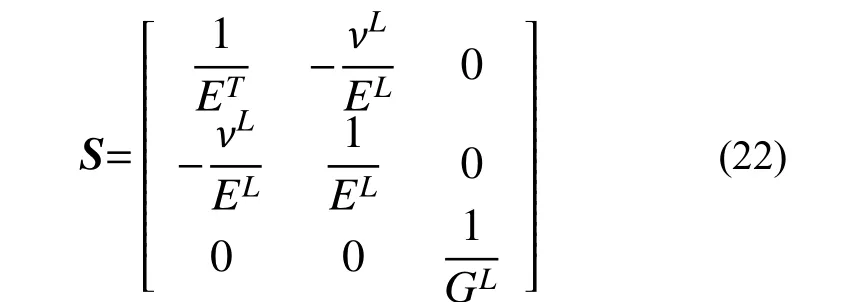
将位移列阵U分解成两部分：

—ROI网格内部节点位移U i，为未知量；

—ROI网格边界节点位移U b，为已知量：取DIC技术测量值(如图11)。

图11 边界条件：ROI 边界节点位移取DIC测量值 u exp ，内部节点位移为未知量Fig.11 Boundary condition:displacement field u exp measured by DICtechnology is imposed on the edge nodes of the ROI,while the displacement field of the interior nodes is unknown

3 测量结果与分析

3.1 材料参数计算准则

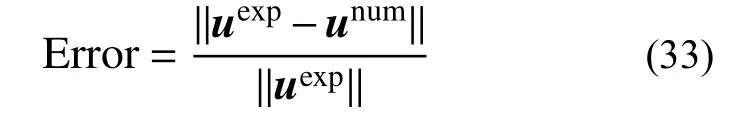
图12 展示了代表样品B14第7张照片(对应荷载180 N)分析结果的函数Error 随材料参数(EL,νL)的变化规律，图中红点显示了该函数极小值点所在的位置，此处对应的(EL,νL)即为该样品在特定荷载作用下所获取照片的分析结果。

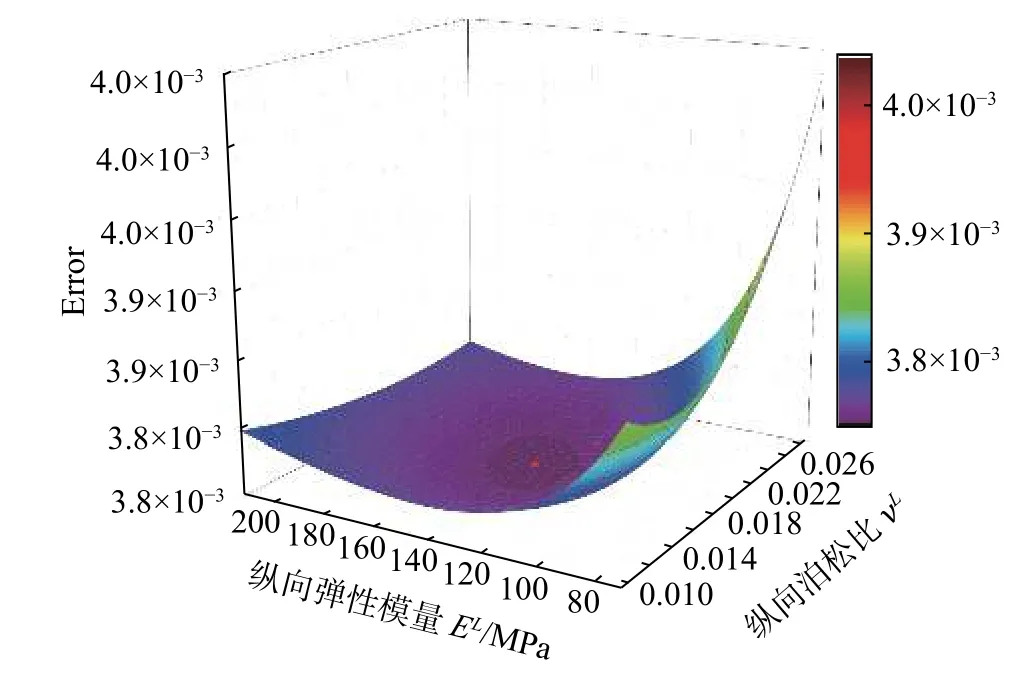
图12 相对误差函数Error 随材料参数(EL,νL)的演变，红点处对应函数Error 的极小值Fig.12 Evolution of the relativeerror according to the parameters(EL,νL),the red dot is the minimum value of the relativeerror

图13比较了同一样品照片(B14 第7张照片)通过DIC技术测量的位移场uexp，2.2小节中铁木辛柯梁模型三点弯曲问题位移场解析解uana，及2.3小节中FEMU 方法位移场数值解unum。可见三者差异极小，相对误差为千分级，侧面验证了本文介绍的材料参数测量方法的精确度和准确性。

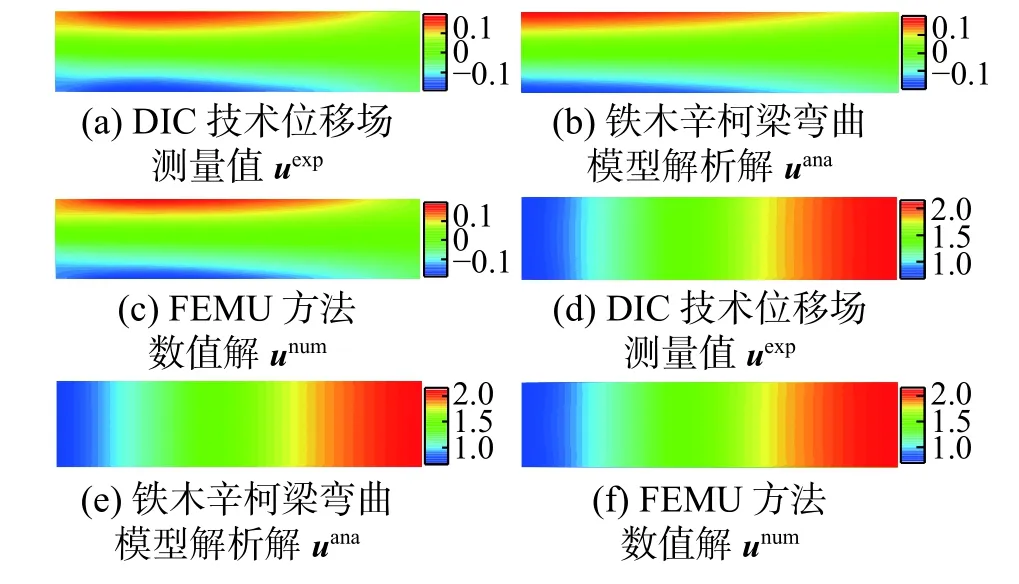
图13 ROI 内位移场的比较Fig.13 Comparison of displacement fieldsin the ROI

3.2 材料参数测量结果

对于全部27个样品，每个样品在试验过程中拍摄了11张照片，第1张照片为样品在初始未受力状态下的参考图像。为了排除加载时由于试验机与样品相接触而造成的扰动影响，并使样品达到稳定状态，每个样品的第2张和第3张照片(对应于荷载F=30 N 和F=60 N)被舍弃不用。

图14为代表样品B14的材料参数(ET,GL,EL,νL)的测量结果，可以看出同一样品在弹性阶段不同荷载作用下获取的8张照片分析结果相似。

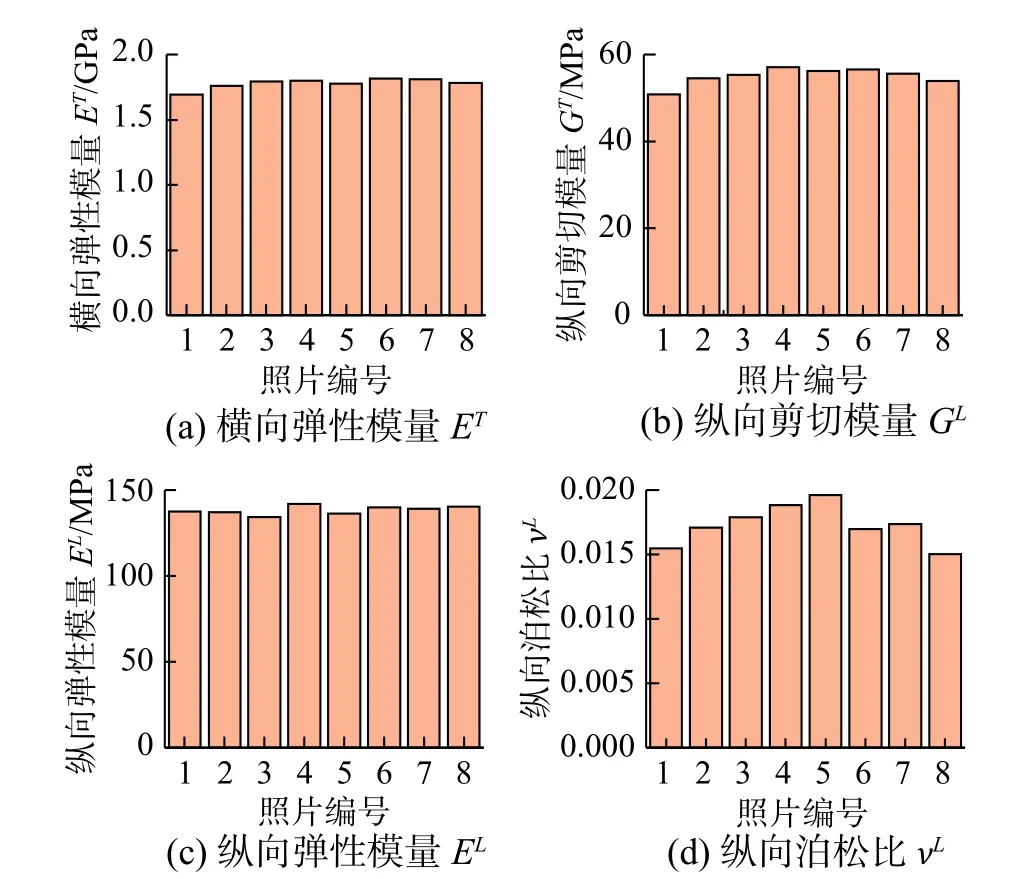
图14 代表样品B14的材料参数测量结果Fig.14 Experimental results obtained for material parameters of the representative sample B14

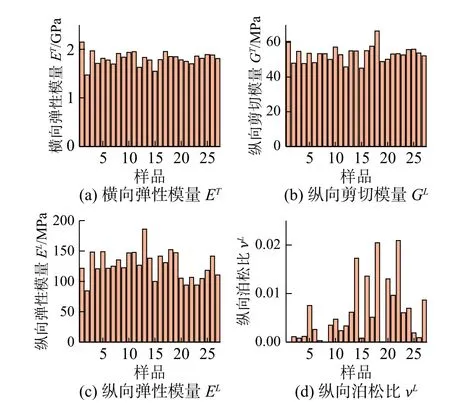
图15 全部27个样品的材料参数测量结果Fig.15 Experimental resultsobtained for material parametersof all 27 samples

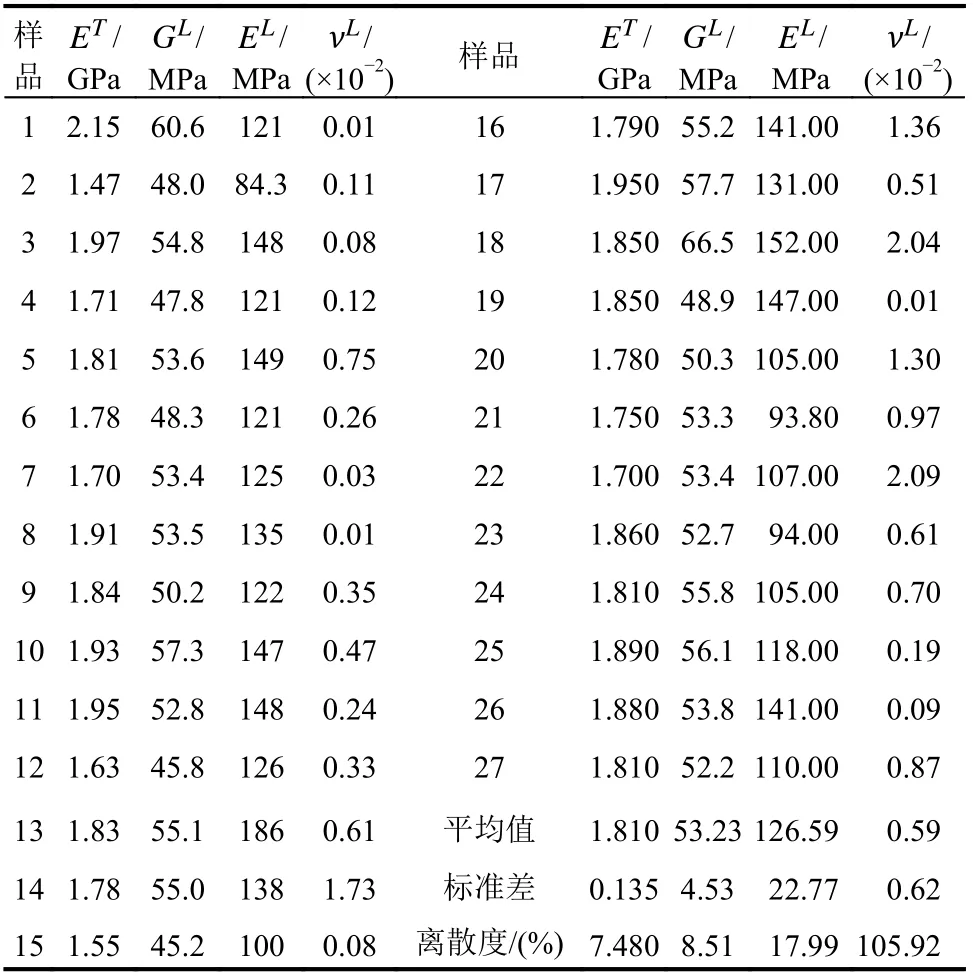
表1 全部样品测量结果统计表Table 1 Measurement results for all samples

通过计算每个试验样品8张图像分析所得到的材料参数的平均值，以代表该样品相应的试验结果。全部27个样品的统计结果见图15和表1。可以观察到试验测量的纵向泊松比νL值很小，且表现出极大的离散性，离散程度(即变异系数，系标准差与平均值之比)为105.92%。本文介绍的测量方法无法计算横向泊松比νT，这是因为梁在yz平面内的弯曲问题(图9)的解答无法给出该参数值。值得注意的是，Moarcas和Irle 在文献[3]中也提到：在关于刨花板材料的弹性特征中，泊松比可能是研究得最少的一项参数，目前尚未提出一种确定木基复合材料泊松比的标准方法。Bodig和Jayne[6]指出：木板产品的横向泊松比νT通常在0.1至0.3的范围内。此外，对比表1与文献[4,17− 18]所记载的刨花板材料参数测量值发现，通过本文方法确定的4个材料参数值(ET,GL,EL,νL)与之具有相同的数量级且取值合理。

4 结论

刨花板作为一种木基复合材料，其材料性质表现出明显的各向异性特征。参考刨花板的制作工艺及其物理构造，本文在弹性阶段将各向异性的刨花板简化为横观各向同性材料，并根据广义胡克定律得知决定其力学性能的材料参数主要有5个：纵向、横向弹性模量EL、ET，纵向、横向泊松比νL、νT及纵向剪切模量GL。

由于其材料表面的多孔性，传统的粘贴应变片的测量方法多有不便，涂胶量不能过多或过少，胶层过厚会影响应变片性能，涂胶过少则粘贴不牢不能准确传递应变。本文结合数字图像相关(DIC)技术，对27个刨花板材料梁式样品进行了三点弯曲力学试验，并利用基于MATLAB 软件开发平台自主编写的三节点三角形网格化DIC(T3-DIC)程序对采集的数字图像进行分析，测量了感兴趣区域(ROI)内网格节点的位移场。对比铁木辛柯梁模型弯曲问题在相同ROI内位移场的解析解，利用最小二乘法测量了ET和GL。通过有限元模型修正(FEMU)方法确定了材料参数EL和νL，使ROI内网格节点位移的有限元数值解与DIC测量值的离差平方和最小。参考相关文献资料，对比本文的试验结果，验证了本文测量方法的可行性与准确性，可作为一种非接触式的全局性测量方法，应用于刨花板材料并推广至各向异性材料的弹性参数测量之中。

考虑到本文所提出的研究方法的局限性，刨花板的横向泊松比νT未能被测量，为此展望如下：结合三维数字图像相关技术，测量物体每个表面点的三维位移分量，通过对比3D有限元数值模拟结果，从而实现对刨花板全部材料参数的测量。目前，双CCD镜头的三维DIC测量及有限元数值分析都是相对成熟的技术。本文相关研究尚处于研究初期，仅以二维DIC测量为基础做了一些试探性的探索工作。

基于目前国内针对刨花板材料力学性质的研究甚少、试验方法欠缺的现状，本文进行了尝试性的研究工作，期望能为相关国内标准的制定及规范的完善提供参考意见。