基于键基近场动力学理论的单裂纹圆孔板冲击破坏研究

刘 宁，胡梦凡，周 飞

(南京理工大学机械工程学院，南京210094)

岩石是隧道、矿山、钻探等大型工程中的主要研究对象，研究其裂纹的起裂、扩展与止裂的规律具有极其重要的意义。动态断裂韧度是控制裂纹扩展的主要参数之一，其数值对工程设计与研究具有重要价值[1−2]。

研究岩石动态断裂行为常用爆炸冲击加载[3]，落锤冲击加载[4]，分离式霍普金森杆(SHPB)冲击加载[5]等，其中分离式霍普金森杆加载目前被广泛用来研究材料的动态断裂行为。倪敏等[6]利用分离式霍普金森杆，采用实验-数值法与准静态法对比研究了单裂纹圆孔板(SCDC)的断裂韧度，对裂纹动态扩展过程研究较少。杨井瑞等[7]研究压缩单裂纹圆孔板试样，提出实验-数值-解析法解算试样起裂韧度和扩展韧度，并研究了试样动态止裂问题。曹富等[8]研究受冲击压缩单裂纹圆孔板裂纹起裂、扩展、止裂和二次起裂过程，用实验-数值-解析法确定起裂韧度、扩展韧度、止裂韧度和二次起裂韧度。李炼等[9]采用霍普金森杆加载系统对偏心圆孔单裂纹圆盘的裂纹扩展进行试验，采用实验-数值-解析法得到动态应力强度因子，分析裂纹起裂、扩展和止裂的全过程。Wang 等[10]提出单裂纹半圆试样(SCSC)，进行纯I型和混合I/II 型岩石的动力断裂实验，并用AUTODYN 软件模拟裂纹扩展行为。为了更好的观测止裂情况，Wang 等[11]采用一种新的V 型底单裂纹半圆试样(VBSCSC)，能有效抑制裂纹的扩展，采用ABAQUS软件计算了应力强度因子，利用实验-数值法确定动态断裂韧性。David 等[12]研究了透明材料在动态载荷作用下裂纹扩展规律，采用XFEM 法模拟实验结果。Ai等[13]研究了巴西圆盘岩石试样在霍普金森压杆作用下裂纹扩展规律，采用动态电阻应变仪和高帧相机进行测试，采用近场动力学方法进行数值模拟，揭示了岩石材料在高应变率载荷作用下的断裂行为和机理。

传统数值方法如有限元方法(FEM)、有限差分法(FDM)等，基于空间连续性与局部接触作用假设建模，通过空间微分方程求解问题，但在处理裂纹扩展、冲击破坏等不连续问题时，还存在相当大的困难[14]。近场动力学理论(Peridynamics,PD)由美国Sandia 国家实验室Silling 教授首次提出[15−16]，基于非局部作用思想建模，用空间积分方程来描述物质点的运动，对于从连续到非连续、微观到宏观的力学行为具有统一的表述，数值上天然具有无网格属性和不连续求解功能，在分析不连续问题时具有较大的优势[17−18]。在霍普金森杆冲击单裂纹圆孔板研究中通常采用实验-数值法[6−9]，需先通过实验测得作用在试件上的加载力，再利用有限元程序计算得到试件的动态断裂韧度。而本文采用键基近场动力学方法(Bond-based PD)建立霍普金森杆冲击加载、试件多裂纹发展全过程近场动力学模型，实现了一体化数值仿真，在裂纹模拟适用性和方法便捷性等方面均具有较大优势。

1 近场动力学理论

1.1 基本思想

如图1所示，设在任意时刻t，空间域R中任一物质点x与其周围一定范围δ(近场范围)内的任意其它物质点之间存在本构力函数f作用，根据牛顿第二定律可得近场动力学方法的运动方程：

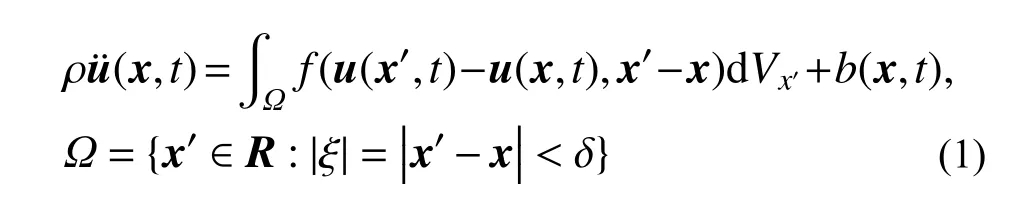
式中：u为物质点位移；u¨ 为物质点加速度；b为体力密度；ρ为材料密度；dV x′表示物质点x′处的体积微元；f为物质点x与x′之间本构力函数，定义物质点间相对位置ξ 及相对位移η 为Ω：

图1 物质点间相互作用关系Fig.1 Grid relationship in PD model

对于键基近场动力学模型，式(1)中物质点间的本构力函数f可以写为：

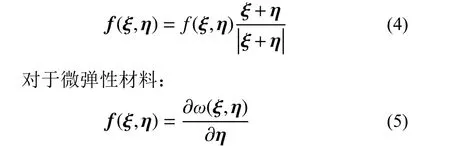
式中，ω(ξ,η)为点对势函数：

式中：c(ξ)表示微观弹性模量；s表示物质点对的伸长率。

式中，G0为材料的断裂能。

引入物质点对的破坏情况占比φ来表示此局部破坏水平：

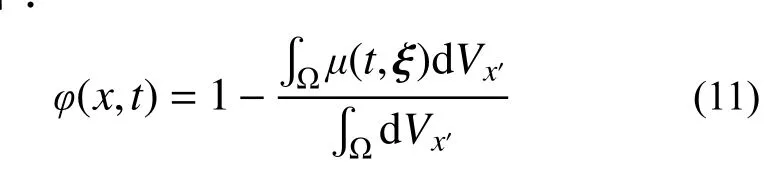
对于均质各向同性材料，将物质点对势能与传统弹性力学应变能等价，可得微观弹性模量c表达式，对于本文试件冲击压缩二维平面应力问题：

式中：E为弹性模量；ν表示泊松比。

霍普金森杆为大长径比结构，可简化为一维PD模型研究，微观弹性模量表达式为：

1.2 数值方法

将岩石板离散为物质点，运动方程式(1)的离散形式可表示为：

时间步长采用文献[16]公式计算：

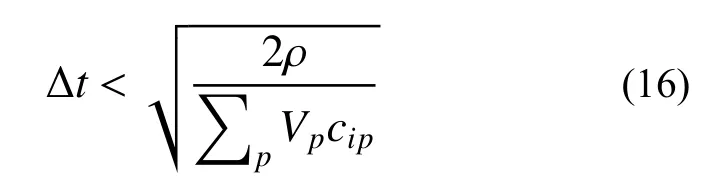
其中，cip=c(xp−xi)。

2 仿真模型

2.1 单裂纹圆孔板冲击模型

根据文献[6]分离式霍普金斯杆冲击单裂纹圆孔板(SCDC)试验装置，如图2所示，建立单裂纹圆孔板冲击破坏PD模型。试件弹性模量为17.67 GPa，密度为3055 kg/m3，几何尺寸如图3所示，试件左端面到圆心的距离L1=42 mm，右端面到圆心的距离L2=121 mm，试样宽度w=80 mm，圆孔直径D=15.5 mm。

图2 霍普金森杆冲击加载实验装置Fig.2 Schematic view of the SHPB

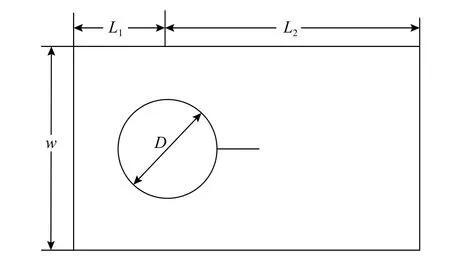
图3 单裂纹圆孔板试样几何形状Fig.3 Geometric configuration of single cleavage drilled compression specimen

霍普金森压杆直径为D=100 mm，入射杆长为4500 mm，透射杆长为2500 mm，压杆弹性模量E1=210 GPa，泊松比ν1=0.3，密度ρ=7850 kg/m3，可求得波在入射杆及透射杆中理论上的传播速度：

应力波从入射杆传播至试样需870µs。为了提高求解效率，入射杆及透射杆采用一维PD模型，SCDC采用二维PD模型，数值离散后一维杆模型节点间距∆xH=0.5 mm，取其临域半径δ=2.2mm；二维模型离散后节点间距Δx=0.5 mm，临域半径δ2=1.65 mm，键临界伸长率s0=0.0042。时间步长统一取Δt=2×10−7s。

2.2 碰撞模型

式中：A=(πD2)/4为压杆的截面积；h为试件厚度。

同理可写出试样右端和透射杆之间的受力模型：

2.3 整形器模型

为了改善加载波形，优化试样受到的激励信号，实验中采用波形整形器来过滤波形中的高频信号，在进行数值模拟时也需考虑整形器影响。通常采用铜作为波形整形器，Frew 等[20]给出了其应力-应变关系：

其中，σ0=625 MPa，n=0.32，m=4.25，计算应力-应变关系如图4所示。卸载过程是弹性的，其弹性模量E=117 GPa。

图4 铜的应力-应变关系曲线Fig.4 Stress-strain curve of copper

冲击部分各部件的尺寸和材料参数如表1所示。

表1 材料参数Table 1 List of Material Properties

在碰撞过程中整形器发生形变，其横截面积可以表示为：

式中：L0为整形器初始长度；A0为整形器初始截面积；L为变形后的长度，等效应力随横截面尺寸的改变而改变：

图5给出了不同撞击速度下应变波形的曲线图，从图中可以看出撞击速度越大，应变峰值越高，到达峰值所用时间越短，采用整形器模型所得的波形曲线较平滑，波形得到明显改善。

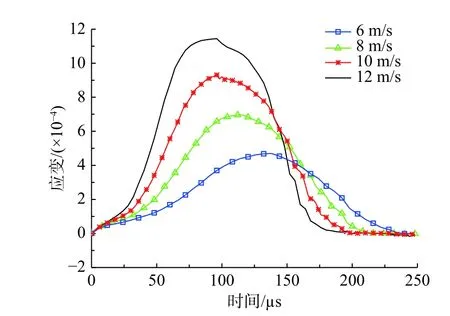
图5 不同撞击速度波形图Fig.5 Strain curvesof different impact velocities

3 数值仿真结果及分析

3.1 不同撞击速度裂纹扩展过程

试件预制裂纹长度为25 mm，采用不同的加载速度撞击，研究试件裂纹扩展过程和破坏模式。当撞击速度较小时，主裂纹沿着预制裂纹方向扩展将岩石一分为二，应变能集中于裂纹尖端以及中心圆孔上下两端，随着主裂纹扩展完成后，次生裂纹逐渐产生，从中心圆孔上下两端萌发，逐渐向上下贯穿将岩石分为四片，如图6所示；当撞击速度较大时，主裂纹仍然沿预制裂纹方向迅速扩展，应力波传播至右端面反射回与入射波相互作用，导致圆孔左上部分与右下部分应力集中，最终产生剪切破坏形成U 型裂纹，与此同时主裂纹停止扩展(止裂)，之后主裂纹起裂继续扩展直达右端面，主裂纹扩展完成后次生裂纹逐渐产生，如图7所示。图8为数值模拟裂纹扩展结果与文献[6]实验结果的对比，二者具有较好的一致性。

3.2 试样端面受力分析

预制裂纹长度为10 mm，当撞击速度为9.43 m/s时，数值模拟所得入射杆与透射杆中应变波如图9所示，和实验数据吻合较好[6]。

图10表示撞击速度为9.43 m/s时试件左右端面所受应力随时间变化的云图。靠近圆孔的左端面，受到冲击后端面受力逐渐增加，且由于中间部分向内凹陷，中间部分受力较两端小，当试样裂纹开始扩展时，端面受力极其不均匀，受力状况呈V 形分布，中间局部区域甚至处于不受力状态；远离圆孔的右端面，在前期受力分布相对均匀，由于裂纹不断扩展，试样逐渐被分为两块，中间部分向会内凹陷，受力较小。

对比文献[6]采用叠加法进行试样端面的平面加载情况，本文模型得到的裂纹起裂后的端面受力和形变分布极不均，充分反映了试件冲击破坏期间复杂的动态响应过程。

3.3 裂纹扩展过程分析

对SCDC 试样主裂纹的扩展情况进行研究，对比试验得到的起、止裂时间及裂纹的扩展特点，分析SCDC的起止裂规律。

图6 冲击速度为6 m/s时试件裂纹扩展过程Fig.6 Crack propagation contour for impact velocity of 6 m/s

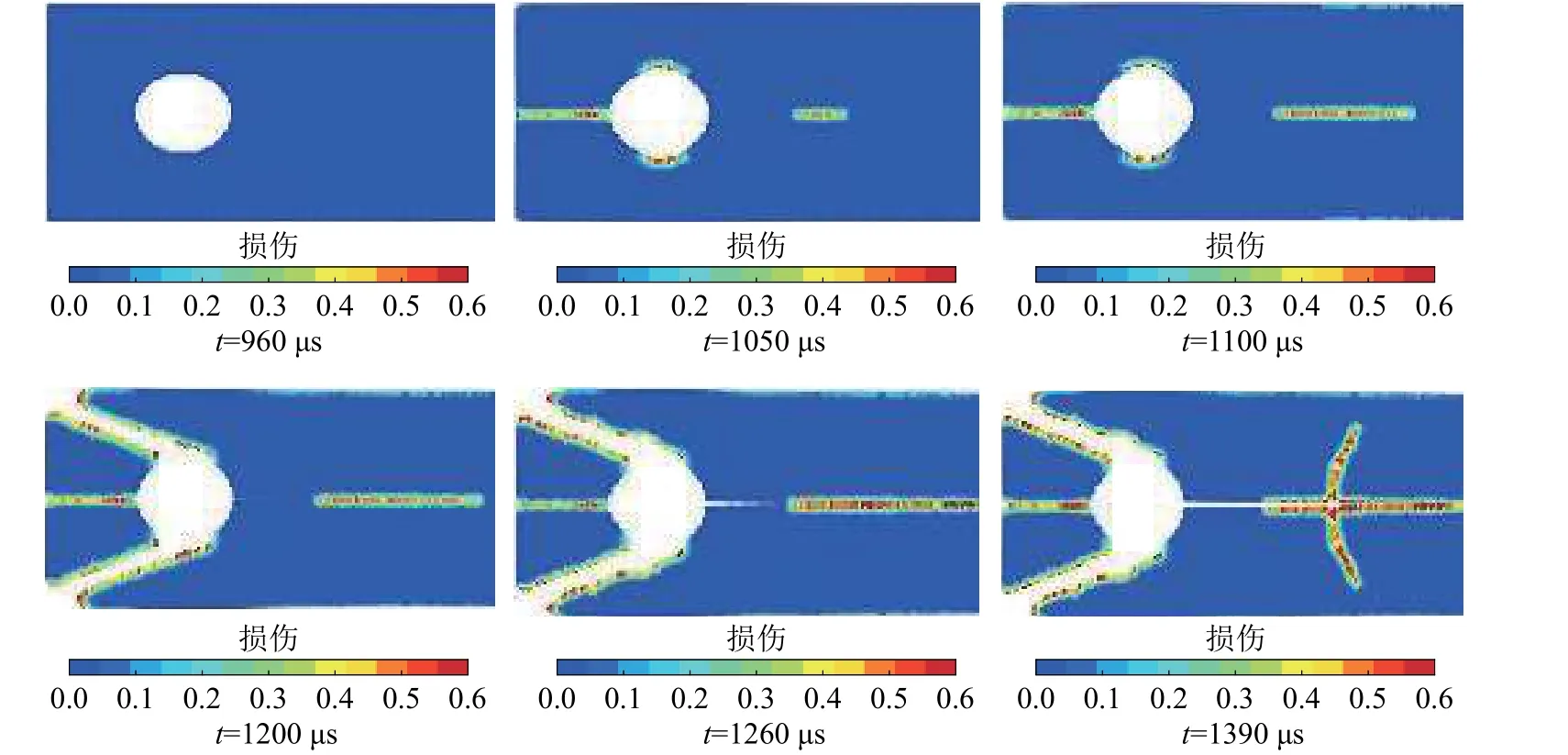
图7 冲击速度为12.5 m/s时试件裂纹扩展过程Fig.7 Crack propagation contour for impact velocity of 12.5 m/s

图8 数值模拟与实验结果对比[6]Fig.8 Comparison of the numerical results against the experiment results[6]

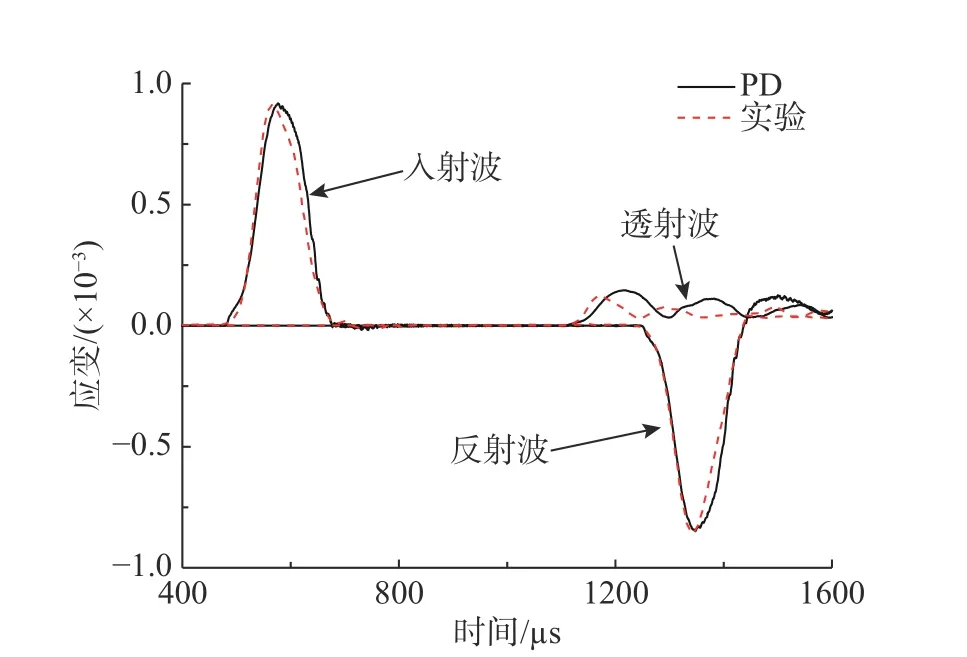
图9 入射杆与透射杆上应变波信号Fig.9 Comparison of the strain signals between the incident bar and the transmission bar

图11与图12给出了撞击速度为9.43 m/s时裂纹的扩展长度、扩展速度随时间变化情况。预制裂纹在973µs时起裂，然后迅速扩展，中途会出现止裂现象，在止裂前扩展速度会逐渐下降。在1164µs时出现二次起裂，裂纹扩展速度瞬间增加，而且二次起裂后的扩展速度较第一次扩展速度大，扩展速度处于不稳定状态。裂纹尖端的时程曲线与实验吻合较好。

为了研究裂纹扩展过程与撞击速度的关系，图13给出了不同撞击速度下裂纹扩展长度时间曲线，可见裂纹扩展都经历了起裂-扩展-止裂-二次起裂的全过程，撞击速度越大，起裂时间越短，第一次止裂时裂纹扩展的长度更长；当撞击速度较低时，裂纹会产生多次止裂现象，第一次加载时裂纹扩展一段距离后止裂，试样获得的能量不足以使裂纹发生二次起裂，等到应力波在入射杆中传播一个来回后再次加载，试样得到足够的能量才能导致二次起裂，因此裂纹会扩展较长的时间(≈1680µs)。

图10 试样端面受力分布(v0=9.43 m/s)Fig.10 Stresscontoursof the left and the right end surfaces(v0=9.43 m/s)

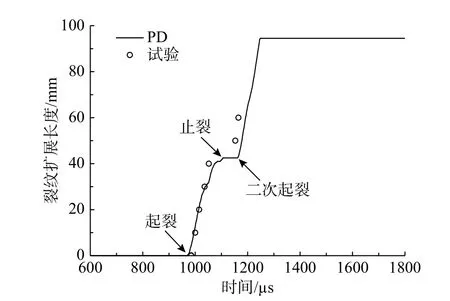
图11 裂纹扩展长度曲线Fig.11 Curve of crack length

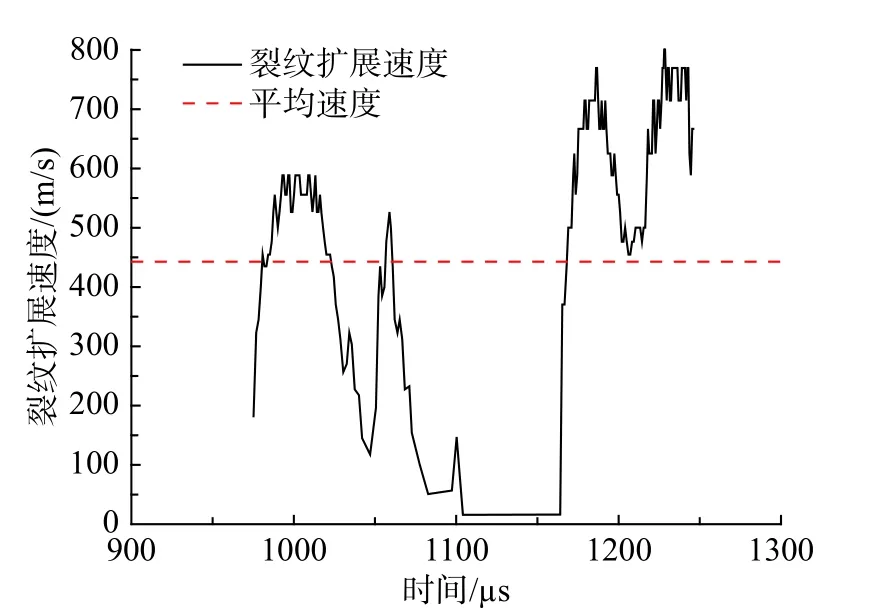
图12 裂纹扩展速度曲线Fig.12 Curveof crack velocity

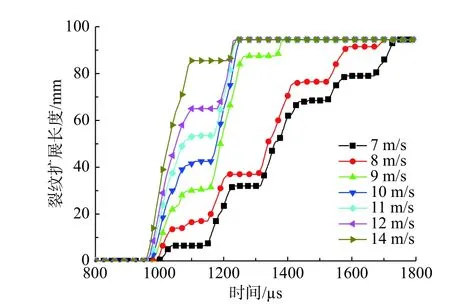
图13 不同撞击速度下裂纹扩展情况Fig.13 Crack growing comparison ofdifferent impact velocities

4 动态应力强度因子计算

通过PD理论计算J积分的方法已有报道[21−23]，对于键基PD理论，采用Hu 等[22]提出了裂纹尖端J积分方法：

为了验证本文动态应力强度计算结果的合理性，首先对经典Chen 的问题进行了分析，结果如图14所示，与Murti 等[24]的求解结果进行对比，采用PD方法计算的动态应力强度因子与其吻合较好。因此本方法可用于SCDC模型的应力强度因子计算。

图15给出了撞击速度为7 m/s时试件动态应力强度因子曲线。由图13可知，裂纹初始起裂时间为1000µs，此时动态应力强度因子为2.9 MPa∙m1/2，二次起裂时间为1147µs，对应的动态应力强度因子为3.24 MPa∙m1/2。在裂纹扩展的时候，能量释放，裂纹尖端的应力强度因子大小逐渐下降，直至裂纹止裂后，裂纹尖端能量逐渐积累，其应力强度因子大小逐渐增加，直至超过二次起裂韧度后再次起裂。

进一步计算了不同撞击速度下裂纹的起裂韧度，如图16所示，可以看出，试件动态起裂韧度随撞击速度的增加而增大。

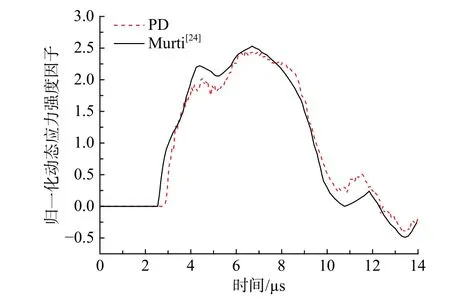
图14 动态应力强度因子算例结果对比[24]Fig.14 Calculated dynamic stress intensity factors[24]

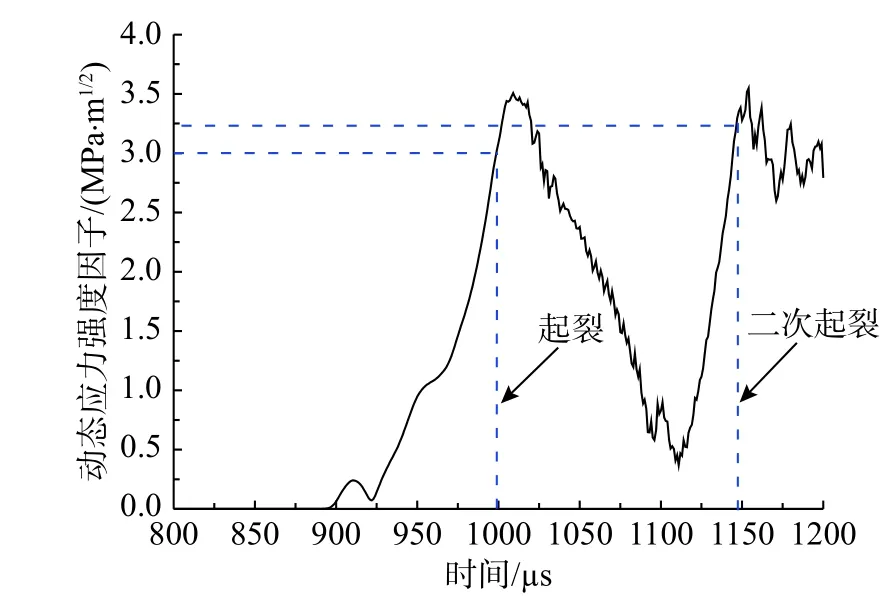
图15 试件动态应力强度因子计算曲线Fig.15 The curve of the dynamic stress intensity factor

图16 不同撞击速度下的动态起裂韧度Fig.16 Crack initiation toughnessunder different impact velocities

5 结论

本文建立了分离式霍普金森杆冲击单裂纹圆孔板(SCDC)近场动力学模型，模拟了试件动态断裂全过程，获得了裂纹扩展模式和发展规律，与实验结果吻合较好。

(1)受圆孔影响，SCDC试样端面受力不均匀，在裂纹扩展时呈现V 形分布。

(2)SCDC试样冲击破坏过程中，裂纹扩展经历了起裂-扩展-止裂-二次起裂的复杂过程。

(3)加载速度较小时，裂纹呈现十字形，当加载速度较大时，圆孔与左端面之间出现剪切破坏，呈现U 形裂纹。

(4)加载速度越大，起裂韧度越大。

本文方法除了可模拟单裂纹圆孔板破坏过程，对脆性材料双裂纹圆孔板、圆盘冲击、预制裂纹三点简支梁、Kalthoff-Winkler 模型等经典冲击破坏问题的裂纹起裂、扩展、分叉均有较好的模拟精度，相比传统数值方法具有明显优势，可推广应用于更广泛的工程断裂问题研究。