改进的Haar 子带变换双滤波器自适应算法

文昊翔，洪远泉，罗 欢

（韶关学院智能工程学院，韶关，512000）

引 言

自适应算法[1‑2]在系统辨识领域有广泛应用。而在某些系统辨识应用(如回声消除、有源噪声控制)，因系统延时不确定，导致目标系统的冲激响应(Impulse response, IR)序列通常具有稀疏性[3]。即序列虽然包含大量系数，但其中大部分系数为零值系数或极小值以模拟延时；真正产生能量的大幅值系数在时域聚集，且数量只占系数总量极小一部分。

传统的最小均方(Least mean square, LMS) 算法与归一化LMS(Normalized LMS, NLMS)算法不考虑目标系统的稀疏性，用一个长的滤波器辨识IR 序列。过长的滤波器导致自适应系统收敛速度下降，计算复杂度增加[4]。

利用稀疏性可有效解决或部分缓解滤波器过长导致的各种缺陷[5]。双滤波器结构(Dual filter struc‑ture, DFS)[6‑7]是其中一种有效的解决方案。它用一级滤波器W1(k)以低分辨率辨识目标系统以定位活跃系数位置；然后一个短的二级滤波器W2(k)在时域覆盖所有活跃系数，并精确辨识活跃系数。W2(k)通过排除大量非活跃系数参与自适应算法以降低滤波器长度。

目前对DFS 的研究主要针对W1(k)，需解决的问题是：在不降低定位精度的条件下，如何降低W1(k)的长度与计算复杂度。传统的解决办法是对W1(k)的输入信号进行降采样以降低W1(k)长度[8]。但降采样将导致信号频谱混叠，高频分量丢失，不利于W1(k)定位活跃系数。

传统的DCT、FFT 变换等将频域局部化而时域信息完全丢失，因此无法应用于时域定位。小波变换[9]可以同时兼顾信号的时频特性。Haar 小波作为最基本的小波，具有支撑区间不重叠，计算复杂度低等优良特性。通过求取Haar 小波与输入信号的内积，可以同时提取信号的时、频信息。Haar 变换为延时估计、自适应辨识稀疏系统提供了新思路[10]。

针对回声消除应用，Ho 等[11]较早将Haar 应用于辨识稀疏系统。受此启发，Bershad 等结合DFS，提出Haar 子带变换 (Partial Haar transform, PHT)[12]算法。PHT 先在某个尺度对W1(k)的输入信号进行PHT 变换以压缩信号长度，然后再进行自适应滤波，并且Bershad 等从理论上证明W1(k)将最终收敛于IR 序列在该尺度下的Haar 变换系数。

以PHT 为基础，Kechichian 等[13]引入模糊逻辑判定活跃系数位置；Ribas 等[14]则尝试进一步降低算法的计算复杂度。在众多学者的努力下，PHT 已经成为一类自适应辨识稀疏系统的有效算法。

本文提出改进PHT (Improved‑PHT, I‑PHT)算法。新算法以PHT 为基础，通过为W1(k)引入时变收敛步长并优化该步长使后验误差最小化以加快W1(k)收敛速度；然后通过分时保存、计算W1(k) 的归一化因子以降低算法的计算复杂度；最后以回声消除为应用背景对新算法进行实验仿真以验证新算法的有效性。

1 问题描述与相关工作

1.1 自适应系统辨识

目标系统IR 序列记为H=[h1,h2,…,hN]T，其中N为序列长度。记k时刻输入信号向量为X(k)=[x(k-1),x(k-2),…,x(k-N)]T，向量X(k)包含最近N个时刻的输入信号。X(k)与H卷积，卷积结果加上背景噪声v(k)形成系统输出d(k)。

系统辨识需解决的问题为：如何根据X(k)与d(k)估计H。根据自适应理论，可以用一个FIR 滤波器W(k)=[w1(k),w2(k),…,wN(k)]以自适应算法更新其系数以逼近、辨识目标系统的IR 序列。其中LMS 算法系数更新方程为

式中：μ为收敛因子，用于平衡算法的收敛速度与辨识精度。滤波器W(k)按自适应算法更新其系数，经过若干次迭代，W(k)将收敛于目标系统的IR 序列。若记E[]为取数学期望，则有

式(4)为基本的自适应理论，与之相关的详细内容可参考文献[1]。

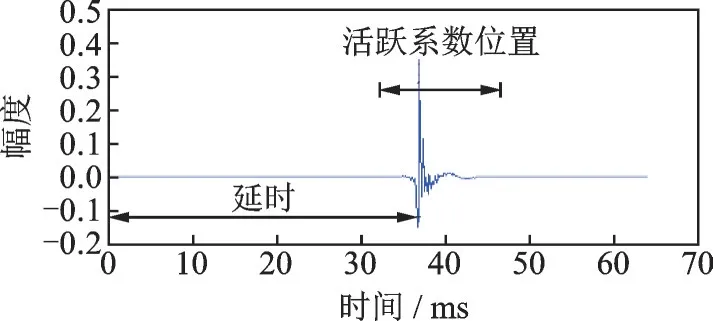
图1 典型稀疏系统的IR 序列Fig.1 Impulse response of typical sparse sys‑tem

1.2 稀疏性与DFS

为保证充分建模，W(k)的长度必须大于等于H的长度。但当目标系统具备稀疏性时，若能获得系统的延时估计，只需精确辨识活跃系数即可完成对整个目标系统的自适应辨识。一个典型稀疏系统的IR 序列如图1 所示[6]。它是电子回声路径的IR 序列，采样频率8 kHz。

DFS 可利用稀疏性提高算法效率，其原理如图2[6]所示。W1(k)以低分辨率辨识目标系统并进行延时估计；然后一个短的W2(k)在时域覆盖所有活跃系数，并精确辨识活跃系数。

1.3 Haar 子带变换

离散Haar 小波母函数定义为

离散Haar 小波定义为

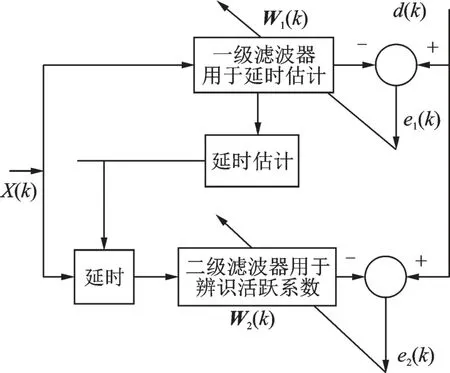
图2 双滤波器结构Fig.2 Dual filter structure

式中：t仅取整数值；m为尺度因子，取值范围1≤m≤log2N，N为输入信号长度，m越大，对应的Haar 时间窗越宽，以利于提取信号低频分量，m越小，则时间窗越窄以提取高频分量；n为时移因子，通过调整n平移小波母函数以覆盖不同的时域范围。

为便于阐述，以输入信号长度N=8 为例说明。Haar 变换矩阵定义如下

式中：第1 列对应m=3，与输入信号求内积后提取信号低频分量；第2、3 列对应m=2，分别提取信号时域前半、后半部分频率信息；第4～7 列对应m=1，分别提取信号对应4 部分的高频分量。

由式(7)可得Haar 子带变换矩阵定义如下

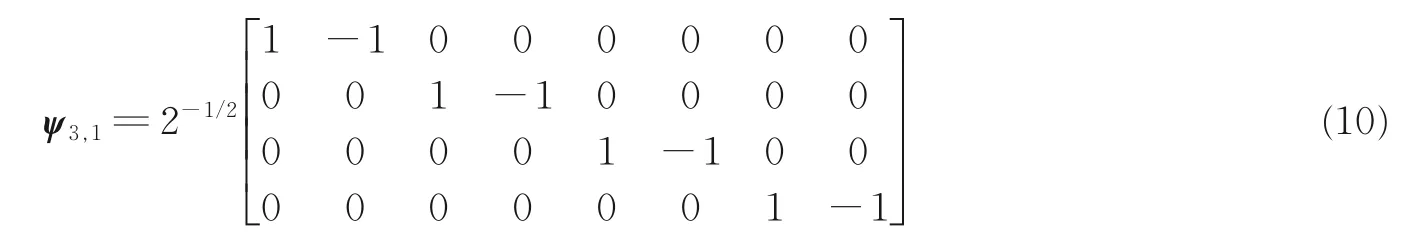
利用Haar 子带变换，Bershad 等[12]提出PHT 算法，W1(k)在Haar 域对信号进行自适应滤波，以降低滤波器长度。系数更新过程为

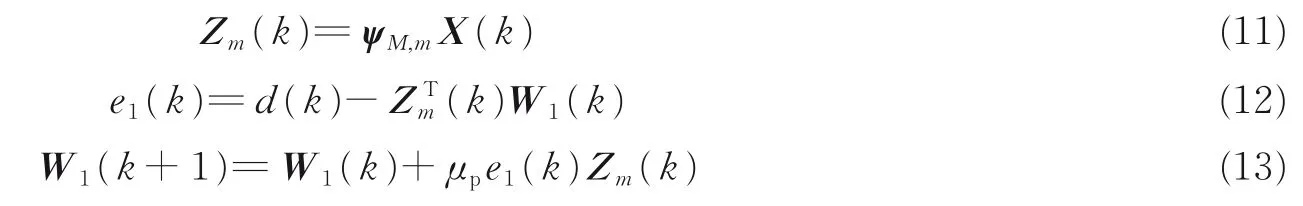
同样以N=8 为例，Haar 尺度因子M定义为M=log2N=3。当取m=3 时，按照式(11) PHT 变换的定义，式(8)的变换矩阵将与输入信号向量X(k)进行矩阵相乘，W1(k)长度N1压缩为N1=1；若m=2，则N1=2；若m=1 时，则N1=4。可得，式(11)的 PHT 变换可大幅压缩W1(k)的长度。

经 Bershad 等证明[12]，W1(k)按式(11—13)进行自适应算法，收敛后有

因此PHT 算法既可压缩W1(k)的长度，又可以获得与目标系统H相关的信息。以W1(k)的信息为基础，再利用峰值系数位置[13]、模糊逻辑[14]或移动窗积分法[15]即可进行延时估计以定位活跃系数。

式(5—14)为PHT 算法的基本原理，与之相关的详细理论推导可参考文献[12]。

2 改进PHT 算法

以PHT(式(11—13))为基础，提出I‑PHT 算法提高W1(k)收敛速度。新算法先为PHT 引入时变收敛步长β(k)，然后以后验误差最小化为目的优化β(k)。

2.1 推导过程

以式(13)为基础引入时变收敛步长β(k)可得

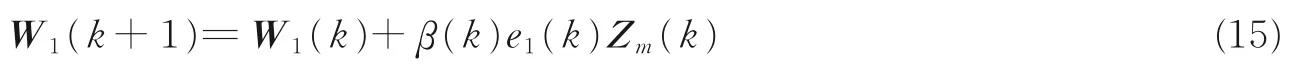
自适应算法的先验误差e1(k)定义如式(12)。后验误差ε1(k)定义为

新算法目的为求取β(k)最优值，使式（17）极大化。

其物理意义为在先验误差e1(k)确定的条件下，使后验误差ε1(k)能量最小化。以下为化简f(β(k))过程。由式(12)可得

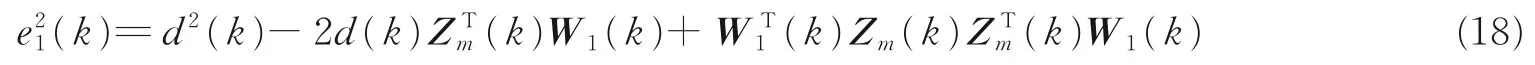
同理，由式(16)可得

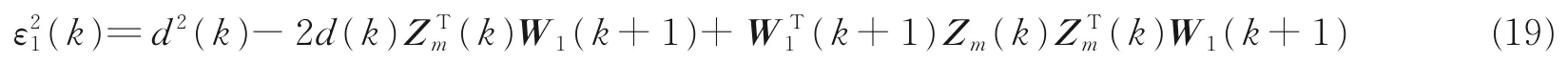
将式(15)代入式(19)，化简、整理后得

式(18)与式(20)两式相减可得

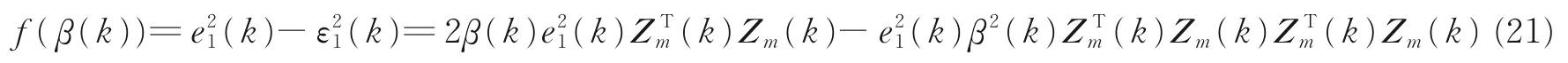
由式(21)可得，f(β(k))是关于变量β(k)的二次函数。对函数f(β(k))关于β(k)求导，当导数为零时，f(β(k))取得极大值，此时β(k)即为最优解。即

解得

将式(23)代入式(15)可得

再次引入收敛步长μi平衡算法收敛速度与稳态失调。最后，新算法的系数更新方程为

2.2 计算复杂度优化

I‑PHT(式(24))与 PHT(式(13))相比，主要是式(24)的分母 [ZTm(k)Zm(k)](即归一化因子)，引入额外的计算复杂度。

在NLMS 算法中，因X(k)与X(k-1)是简单的线性移位关系，可以利用式(25)快速计算归一化因子。

但在I‑PHT 中，因Zm(k)与Zm(k-1)不再满足线性移位关系，因此[(k)Zm(k)]不能直接套用式(25)快速计算获得，需另外寻找新的高效计算方法。

为方便讨论，记Zm(k)=[z1(k),z2(k),…,zN1(k)]。定义压缩比为r=N/N1，式中N为X(k)长度，N1为Zm(k)的长度。通过PHT 变换(式(11))，X(k)中相邻的r个信号被压缩为Zm(k)中的1 个信号。因此虽Zm(k)与Zm(k-1)不再保持线性移位关系，但Zm(k)与Zm(k-r)仍保持线性移位关系。针对该关系，建立向量P= [p1(k),p2(k),…,pr(k)]。记i=1+(kmodr)，式中mod 为求余运算。将(k)Zm(k)值保存在pi(k)中，有pi(k)=(k)Zm(k)。即把算法归一化因子按不同时刻分别保存在向量P中，并以r为循环。此时有

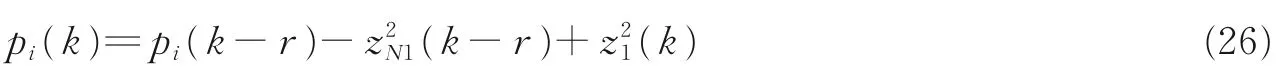
至此，新算法的实现可归纳为按步骤执行式(11,12)与式(27—29)。

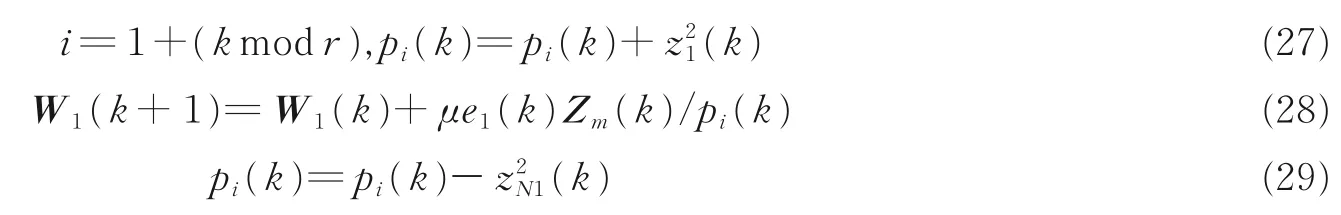
与 PHT 算法相比，I‑PHT 每次迭代仅额外引入 3 次加/减法、2 次乘法。

3 实验仿真

以回声消除为应用背景进行实验仿真以检验新算法的性能。目标系统H采用图1 所示的实际回声路径，长度为N=512。活跃系数定位的判断逻辑采用移动窗积分法[15]。

压缩比r决定W1(k)的长度N1。若r取值过小，则不能有效缩短W1(k)的长度；若r取值过大，则分辨率过低，无法有效定位活跃系数。本实验按文献[13]取r=4，即N1=128。

实验仿真分两部分进行，实验1 检验新算法对W1(k)性能的影响，实验2 检验新算法对整个DFS 的影响。

3.1 实验1

以方差为1 的高斯白噪声作为输入信号X(k)。X(k)与H卷积，再以另一高斯白噪声作为背景噪声v(k)，XT(k)H与v(k)二者信噪比为 20 dB。

实验 1 主要比较 PHT 与 I‑PHT 两种算法。对 I‑PHT，μi=0.5；对 PHT，μp=μi/E[(k)Zm(k)]。其中E[(k)Zm(k)]根据输入信号的先验知识统计获得。对W1(k)的性能评价采用两个指标：失调与有效定位活跃系数所需迭代次数。

(1)失调，单位为dB，计算公式为

式(30)中H1的计算公式为H1=ψM,m H。

两算法的W1(k)失调曲线如图3 所示。由图3 可得，I‑PHT 与PHT 相比，稳态失调相似，但收敛速度有明显提高。

（2)定位活跃系数所需迭代次数。当W2(k)开始覆盖目标系统的峰值系数时，可认为W1(k)已准确定位活跃系数。由图4 所展示的实验得，为准确定位活跃系数，PHT 约需408 次迭代，而 I‑PHT 仅需约 101 次迭代。

图3 一级滤波器失调曲线对比Fig.3 Misalignment curve comparison of the first-order filter

3.2 实验2

因W1(k)仅用于低精度辨识目标系统以定位活跃系数，精确辨识目标系统还需W2(k)完成，所以W2(k)的性能改善才是整个自适应系统的最终目标，对W2(k)性能的评估与W1(k)相比，更显重要。

在计算W2(k)算法失调时，DFS 需先将短的W2(k)在首尾补零扩展至长度为N=512，记扩展后的序列为W(k)，再按式（31）计算失调。

重复实验 1 的参数设置，PHT 与 I‑PHT 的W2(k)均采用LMS 算法更新系数，W2(k)的长度N2=64。μ=0.077。两算法的W2(k)失调曲线如图4 所示。

结合图4 与实验 1 可得，因 I‑PHT 可使W1(k)获得更快的收敛速度，在更短的时间内准确定位活跃系数，所以最终导致W2(k)的收敛速度亦有大幅提高。因PHT 的W1(k)约需400 次迭代才可获得稳定的延时估计，因此其W2(k)只有在400 次迭代之后才进入快速收敛阶段。而I‑PHT 的W2(k)仅需约100 次迭代即进入快速收敛阶段，获得比PHT 更快的整体收敛速度。

为更好地模拟回声消除系统工作环境，以实际语音信号激励目标系统，并再次进行实验仿真。系统信噪比为20 dB。为检验算法跟踪能力，在20 s 时，目标系统IR 序列整体左移 200 个单位。针对W1(k)的收敛步长，I‑PHT 设为μi=0.1；PHT 设为μp=μi/E[(k)Zm(k)]。W2(k)的收敛步长，I‑PHT 与 PHT 均统一设为μ=0.03。单滤波器 LMS算法作为经典的自适应算法亦纳入对比，滤波器长度设为N=512，步长设置为μ=0.03/8。其他设置与实验1 一致。3 种算法的W2(k)失调如图5 所示。

图4 二级滤波器失调曲线对比Fig.4 Misalignment curve comparison of two-stage filter

图5 3 种自适应算法失调曲线对比Fig.5 Misalignment curve comparison of three adaptive algorithms

由于DFS 能有效降低滤波器长度，其W2(k)长度仅为LMS 算法W(k)长度的1/8。随着滤波器长度的下降，算法的收敛速度迅速提高。由图5 得，I‑PHT、PHT 的收敛速度显著高于LMS 算法。

而同为 DFS，针对W1(k)而言，I‑PHT 优于 PHT 的地方主要有以下 3 点：

(1) 因I‑PHT 的W1(k)能更快地定位活跃系数，因此其整体收敛速度明显优于PHT。图3—5 可证明该结论。

(2) 实验发现当输入信号是真实语音信号时，I‑PHT 的W1(k)收敛步长μi取值范围大于PHT 的μp。取μi<0.8 仍能保证W1(k)收敛，但 I‑PHT 必须满足μp<0.1/E[ZTm(k)Zm(k)]才能保证W1(k)收敛。因此 I‑PHT 的稳定性高于 PHT 算法。

(3) I‑PHT 的步长μi取值范围有较清晰的指导值，其理论取值范围为0<μi<1。当输入信号为高斯噪声时，该理论范围可保证W1(k)收敛；当输入为强相关、非平稳的语音信号时，各种自适应算法的稳定性均会减弱，此时I‑PHT 的μi实验取值范围约为0<μi<0.8。但PHT 算法需先获得E[ZTm(k)Zm(k)]的先验知识，才能确定μp的取值范围。因此，与PHT 算法相比，I‑PHT 更易于实现。

4 结束语

针对稀疏系统辨识应用，DFS 是一类有效的解决方案。它用W1(k)定位活跃系数位置，用一个短的W2(k)精确辨识活跃系数。它通过降低滤波器有效长度，以达到提高收敛速度，降低计算复杂度的目的。

本文主要针对W1(k)进行讨论，提出I‑PHT 算法。新算法先对W1(k) 的输入信号进行PHT 变换以压缩信号长度；然后引入时变步长，并以后验误差最小化为目标函数优化时变步长；最后将新算法的归一化因子分时、循环保存到一个向量中，并通过自回归方式维护归一化因子以降低计算复杂度。

以回声消除为应用背景对I‑PHT 进行实验仿真，仿真结果表明，DFS 能有效降低滤波器长度以提高收敛速度。而与PHT 相比，I‑PHT 算法收敛速度与稳定性均有明显提高。