基于迭代p 阈值投影算法的压缩感知磁共振成像
杜秀丽 ,刘晋廷 ,吕亚娜 ,邱少明
(1.大连大学通信与网络重点实验室,大连,116622;2.大连大学信息工程学院,大连,116622)
引 言
磁共振成像(Magnetic resonance imaging,MRI)[1]在临床诊断中扮演着重要角色。尽管MRI 可以提供具有优异软组织对比度信息的高质量图像,但其成像速度不尽如人意,主要是因为受到物理上(如梯度脉冲的幅度和变化率)以及生理上(神经刺激)的约束。压缩感知技术(Compressed sensing,CS)[2]被引入到MRI 中用以显著提升成像速度,称其为CS⁃MRI。近年来,在磁共振成像领域越来越多学者开始使用冗余变换。紧标架[3]的冗余变换提高了对复杂图像的稀疏表示能力。文献[4]提出了一个简单而有效的基于紧标架的压缩感知磁共振图像重建算法——快速迭代软阈值投影算法(projected fast iterative soft⁃thresholding algorithm,pFISTA),它借鉴了快速迭代软阈值算法(Fast iterative soft⁃thresh⁃olding algorithm,FISTA),利用编程使得pFISTA 避免存储整个冗余系统下的表示系数,因此pFISTA可以处理高冗余度变换下的大规模MRI 重建问题。pFISTA 的另一个优点是重建误差对步长不敏感,因此可以在磁共振图像重建中广泛应用于不同的紧标架。与迭代软阈值算法(Iterative soft⁃threshold⁃ing algorithm,ISTA)[5]、FISTA[6]、光滑化的快速迭代软阈值算法(Smoothed FISTA,SFISTA)[7]、基于Moreau 包络的近似平滑迭代算法(Proximal smoothing iterative algorithm,PSIA)[8]、交替方向乘子法(Alternating direction multiplier method,ADMM)[9]相比取得了比较好的重建效果。文献[10]进一步证明了并行成像版本的pFISTA 的收敛性,特别证明了由pFISTA 求解的两个著名的并行成像重建模型SENSE 和SPIRiT 的收敛性。文献[11]提出了pISTA-SENSE 残差网络来解决并行磁共振成像重建问题。但以上算法中采用的软阈值函数收缩功能较差,导致成像速度慢、质量差。
文献[12]提出了一种有效的p阈值算法,使用p阈值替换ISTA 中软阈值来解决稀疏信号恢复问题,并证明了所提出算法的全局收敛性。文献[13]建立了用于恢复稀疏信号的确切条件。Li 等[14]提出用迭代奇异值p阈值算法来解决低秩矩阵恢复问题,并使用随机奇异值分解给出了它的两个加速版本。文献[15]提出了一种基于交替方向法的算法——迭代p阈值算法,用于解决低秩张量恢复问题,进一步证明了迭代p阈值算法的有效性;并得出:最小化p阈值算子的惩罚函数是经典凸L1范数和非凸Schat⁃ten⁃p范数的良好替代。
针对pFISTA 使用的软阈值函数收缩功能较差的问题,本文利用p阈值对小系数的惩罚更大、对大系数产生较小偏置的优势,提出迭代p阈值投影算法(projected iterativep⁃thresholding algorithm,pIp⁃TA),并利用文献[6]中的Nesterov 加速方法,提出快速迭代p阈值投影算法(projected fast iterativep⁃thresholding algorithm,pFIpTA),以提高有效提高MRI 的重构精度和重构速度。
1 迭代软阈值投影算法
1.1 紧标架下CS‑MRI 的重建模型
CS⁃MRI 对全采样k空间数据进行欠采样,数学模型可以表示为

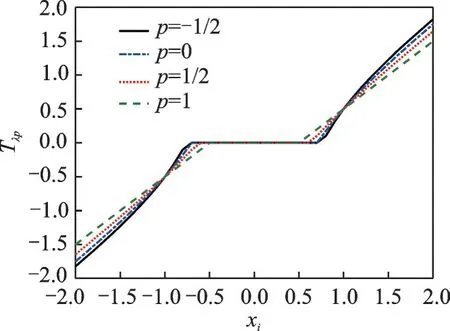
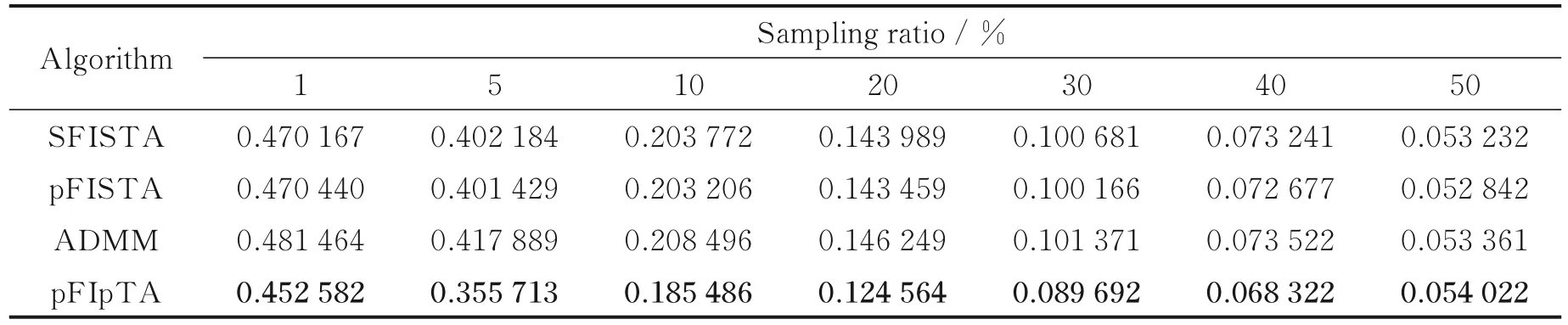
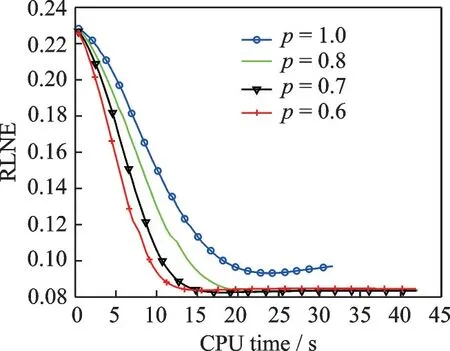
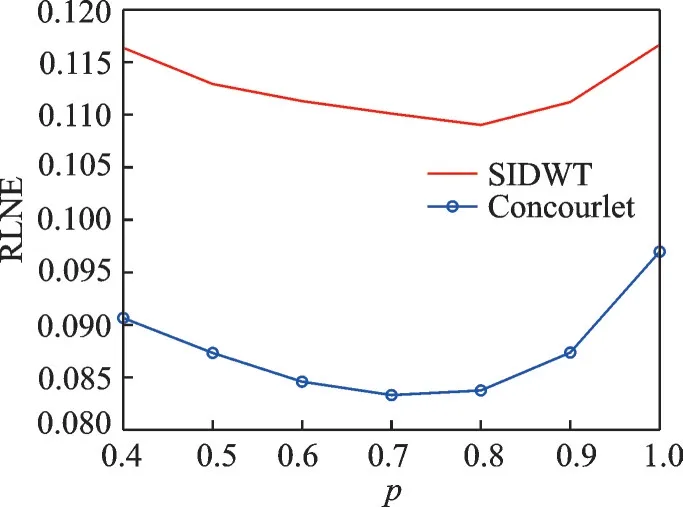
式中:y∈ CM表示采样得到的k空间数据,U∈ RM×N(M 磁共振图像本身不具有稀疏性,磁共振图像的稀疏性有两种表现:一种是被某个字典中的原子信号稀疏表示,另一种是经过某个变换后是稀疏的,因此也对应有两类重建模型:综合型和分解型[16]。 综合型 分解型 式中:Φ表示标架,当Ψ正交且满足Φ=Ψ*=Ψ-1时,综合型模型和分解型模型重建效果相同。α为标架表示的图像系数,λ为正则化参数,权衡稀疏项和数据保真项,标架能够有效地利用图像的冗余信息实现图像信息与噪声的分离,通过求解‖Ψx‖1L1范数的凸优化问题重构出高质量的图像,通过求解范数的数据保真项来拟合噪声。 为了联合紧标架下分解型和综合型模型,文献[16]同时给出了平衡型重建模型,即 式中:ΦH表示一个分解矩阵,当ΦHΦ=Ι时,称Φ为标准紧标架,β为一个近似参数。 文献[4]提出,pISTA 先将分解型模型改写成一个形似综合型模型的等价模型,如式(4)所示,然后计算目标函数中非光滑项的近邻映射,并引进Beck 和Teboulle 在文献[6]中提出的加速策略,得到快速迭代软阈值投影算法。 pISTA 和pFISTA 实际求解的是平衡型模型式(4),而不是精确的分解型模型。对于平衡型模型式(4),首先令 对式(4)中的最小化问题应用ISTA 就需要求解如下的近邻映射(Proximal map)[5] 式中:γ为步长,αk+1表示第k+1 迭代的系数,FH为离散傅里叶反变换,UT为U的转置。prox 表示近邻映射,其定义为 式中:z表示重建图像,x表示磁共振图像,f代表一个基于L1范数的函数。对于综合型模型,f(z) =‖z‖1,因此近邻映射即为 式中:Tλ(⋅)代表对每一个数值计算的软阈值函数,即 式中:sgn(xi)表示符号函数,xi表示x其中一个元素,即当xi>0 时为 1,当xi<0 时为-1;λ表示阈值。 将式(8)的左右两边同乘以Φ,同时令xk+1=ΦTλ(ΦH(xk+γFHUT(y-UFxk))),可得 式中:xk+1表示第k+1 迭代的图像。式(12)为pISTA 的迭代公式,再引入FSITA 的加速策略就可以得到pFISTA。 不论是ISTA 还是FISTA,求解惩罚函数的近端映射的迭代广义p阈值算法是求解正则化逆问题的有效算法。 文献[12]提出一种新的迭代p阈值函数 式中:p值表示为xi增加权重的值。p阈值操作函数如图1 所示。 从图1 可以看出,当p<1 时,p阈值函数比软阈值函数对小系数的惩罚更大,而对大系数产生更小的偏差。噪声分量在所有频带中以小系数进行散射[17],在图像重建过程中,通过p阈值函数与小系数之间的比较来抑制小系数进行去噪,从而获得更好的重建图像。当p=1 时,变成了软阈值算子[4],当p→∞时,为硬阈值算子。通过保留大系数来克服软阈值函数容易失真的问题,通过收缩中间系数来减少硬阈值函数不连续。文献[13]已经证明,当p<1 时,稀疏恢复所需的测量比使用p=1的ISTA 情况下少,或者使用相同数量的测量时,使用p<1 可获得更好的质量。 图1 p 阈值函数图Fig.1 Plot of p-thresholding function 惩罚函数的近端映射可以解决正则化反问题,因此软阈值函数作为相应的惩罚函数的近端映射十分有效。p阈值函数可以看作是具有稀疏约束更宽泛的惩罚函数的映射。针对软阈值函数收缩功能较差的问题,本文提出将收缩性能更好的p阈值函数替换pISTA 中的软阈值,并设计了相关的算法。 因此,针对紧标架下模型重建问题设计迭代p阈值算法。迭代p阈值投影算法求解紧标架下模型重建问题模型如式(4)所示,通过1.2 节了解到迭代软阈值投影算法的迭代公式可以解决平衡型模型重建问题,将p阈值替换软阈值,并融入到pISTA 的核心公式中,得到pIpTA 的迭代公式为 式中:Tλp(t)为迭代p阈值函数,λ表示阈值,γ为步长。 通过灵活改变p值来设计新的稀疏目标函数,以获得更好的重建效果。同时,引入文献[6]提出的Nesterov 加速策略,Nesterov 方法采用从上一步迭代点处朝前走一步处的梯度,以极少的额外计算量大幅度提高了迭代p阈值投影算法的收敛速度,从而得到pFIpTA。紧标架下MRI 重建的pIpTA 和pFIp⁃TA 算法分别如算法1 和算法2 所示。 算法1pIpTA 算法 参数:λ,γ 初始化:x0 循环直到停止: 输出:x 算法2pFIpTA 算法 参数:λ,γ 循环直到停止: 输出:x 图2(a)和图2(b)中的脑图均是使用一台3T 的西门子 Trio Tim 磁共振成像仪扫描一个健康的志愿者头部得到的图像,成像仪使用32 线圈,脉冲序列为T2 加权的Turbo 自旋回波序列,两幅图像分别来自第7、10 层,其中TR/TE=6 100/99 ms,FOV=220 mm×220 mm,厚度为 3 mm。其中图2(c)模拟三维成像中的二维相位编码,图2(d)模拟二维成像中的伪放射性线采样,它的采样点都是在笛卡尔坐标的网格上最接近真实放射线采样轨迹的点。k空间数据的中心区域信噪比较高,远离中心区域的噪声较为凸显,因此CS⁃MRI 中的采样模板在k空间的中心采集更多的数据。以上所有数据来源于http://csrc.xmu.edu.cn/。 仿真实验的硬件配置为:因特尔酷睿i5⁃3360M 处理器、主频3.4 GHz、内存16 GB;软件配置为Mat⁃lab 2081b。 利用式(15)定义的相对L2范数误差作为图像重建质量的数字指标。 图2 实验数据集Fig.2 Experimental datasets 3.2.1 pFIpTA 算法性能分析 本文选用平移不变离散小波变换(Shift⁃invariant discrete wavelet transform,SIDWT)作为典型实验中的紧标架,使用的是具有4 个分解尺度的Daubechies 小波。对于实验中所用到的算法,首先需要对其调节参数,这些参数包括:FIpTA 中的步长γFp,SFISTA 中的步长γS和光滑参数μ,pFISTA 中的步长γp。按如下规则设置:γFp=1;根据文献[6],γS=1/(1+1/μ),而μ也根据文献取不同的推荐值;对于pFISTA,根据文献[2],将γp设置为1。pFIpTA 算法中p的值为0.7。 图3 为T2 加权脑图第7 层图像重建结果,其中第1 行为原图和4 种算法得到的重建图像,第2 行第1幅为30%伪放射线采样模板,剩余4 幅为4 种算法的残差图。图中FIpTA,SFISTA,pFISTA 和pFIp⁃TA 的 RLNE 分别为 0.132 426,0.097 078,0.097 029 和 0.083 288。图4 为加权脑图第 10 层重建结果,使用30% 高斯采样模板进行采样。图中FIpTA,SFISTA,pFISTA 和pFIpTA 的RLNE 分别为0.104 166,0.091 703,0.091 573 和 0.069 123。从图3,4 可以看出,FIpTA 的重建图像含有明显的伪影,而SFISTA 和pFISTA 的重建图像中这些伪影被很好地压制了,pFIpTA 中的伪影最少。pFIpTA 的重建误差比其他3 种算法的重建误差要低。对应的收敛曲线如图5,6 所示,所提出的pFIpTA 比pFIS⁃TA,SFISTA 提高了大约0.013 79 个单位。 图3 T2 加权脑图第7 层图像重建结果Fig.3 Recconstructed T2-weighted brain images with #7 图4 T2 加权脑图第10 层图像重建结果Fig.4 Recconstructed T2-weighted brain images with #10 不同的稀疏化磁共振图像的紧标架对CS⁃MRI 的重建误差影响很大。为了全面评估pFIpTA,在本节实验中选用轮廓波(Contourlets)作为紧标架,Contourlets 应用图像的局部边缘方向性来进一步稀疏化图像,使得重建结果能够尽可能保留边缘信息,并和求解分解型模型的通用算法ADMM 进行了对比,实验结果如图7 所示。图中结果显示,和使用SIDWT 作为紧标架效果一样,pFIpTA 比其他的重建误差都要低,而且pFIpTA 收敛更快。因此,pFIpTA 具备pFISTA 的优势不随使用的紧标架而变化,并且效果更好。 图5 T2 加权脑图第7 层图像收敛曲线Fig.5 Convergence curve of T2-weighted brain images with #7 图6 T2 加权脑图第10 层图像收敛曲线Fig.6 Convergence curve of T2-weighted brain images with#10 图7 Contourlets 下的收敛曲线Fig.7 Convergence curve using Con⁃tourlets 因为pFIpTA 求解的是平衡型模型,而非精确的分解型模型,这部分通过对比ADMM,可了解pFIpTA 与分解型重建结果的效果。从图7 可知,SFISTA 和pFISTA 重建误差比ADMM 的重建误差更小,且本文所提pFIpTA 算法收敛速度更快,精度更高。 为了验证本文提出的重构算法在不同采样率下的磁共振图像的重建性能,对不同采样率下SFIS⁃TA、pFISTA、ADMM 和pFIpTA 的重建误差进行了分析。表1 是不同采样率下各算法的重建误差,实验分别采用1%,5%,10%,20%,30%,40%和50%的高斯采样模板,紧标架为轮廓波。从表1 可以看出在1%,5%,10%,20%,30%,40%和50%采样率下,SFISTA 和pFISTA 重建误差差距不大,pFIp⁃TA 与其他3 种算法相比重建误差更小;在50%采样率下,4 种算法重建误差趋于平稳。 表1 不同采样率下重建误差Table 1 Reconstruction error at different sampling ratios 3.2.2p值的选择 本节将从数值实验验证p值如何影响重建速度和重建误差。图8 中,选用p值分别为1.0,0.8,0.7,0.6 时的收敛曲线,p=1 为pFISTA。图9 为在紧标架为SIDWT 和Contourlets 时,取不同p值对应的RLNE。 从图8 和图9 可以看出,随着p值减小,收敛速度变快,但是RLNE 并不遵循这个规律。从图8 可以看出在0.8,0.7 出现拐点,0.8 和0.7 的收敛精度差不多,但是在0.7 时,速度有所提升。图9 中在Contour⁃lets 下所代表的曲线,也表明在0.7 时重建精度更好一点。综合考虑,本文建议将p的值设置为0.7。 图8 PFIpTA 不同p 值的收敛曲线Fig.8 Convergence curve of PFIpTA at different p values 图9 SIDWT 和Contourlets 条件下不同p 值对应的RLNEFig.9 RLNE with different p values under SIDWT and Contourlets 针对迭代软阈值投影算法中软阈值函数收缩功能较差的问题,本文提出了迭代p阈值投影算法和它的加速版快速迭代p阈值投影算法来求解紧标架下的压缩感知磁共振图像重建问题,将收缩性能更好的p阈值函数替换pISTA 中的软阈值。数值实验显示,pFIpTA 的重建结果比SFISTA 和pFISTA的好,而且pFIpTA 收敛速度比pFISTA 更快;与ADMM 相比收敛精度也有一定提高。p阈值具有能灵活的收缩功能,验证了pFIpTA 在p为0.7 时表现出色。pFIpTA 不仅继承了pFISTA 不随使用的紧标架而变化的优势,甚至效果更好,而且继承了p阈值函数的优势,获得了更好的重构效果。


1.2 迭代软阈值投影算法
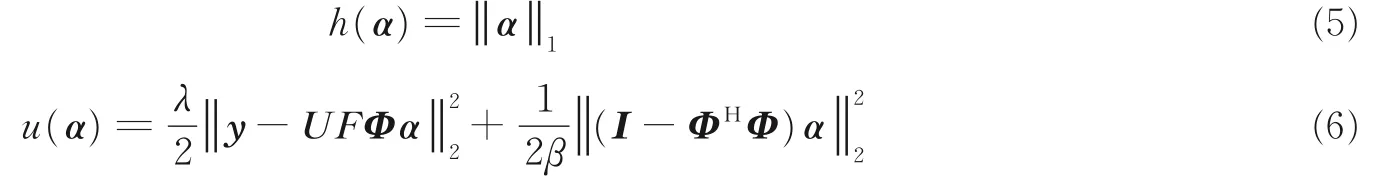




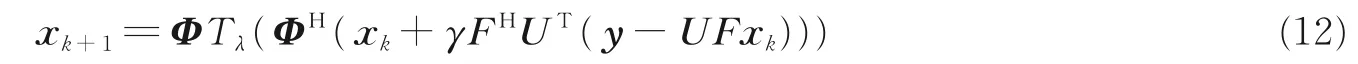
2 迭代p 阈值投影算法
2.1 迭代p 阈值
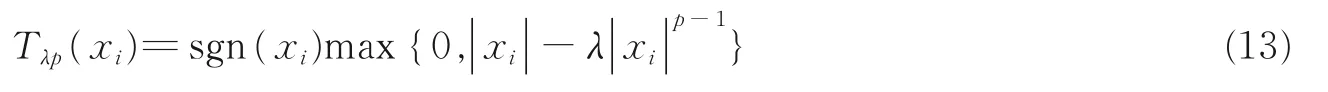
2.2 迭代p 阈值投影算法

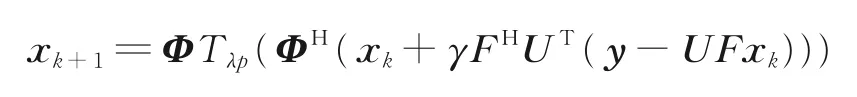
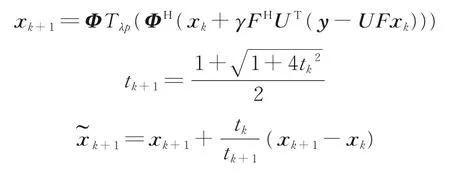
3 实验结果与分析
3.1 实验环境及数据集


3.2 实验结果及讨论





4 结束语

