基于相关分析的电网电能质量缺失数据填充方法*

雷峰津 房 俊

(北方工业大学信息学院，100144，北京)

电网电能质量监测分析系统实时汇集全网电能质量数据，使得数据驱动的电能质量问题分析与决策成为可能. 但电网监测终端数量多、存储系统组成复杂、物理环境恶劣等原因都会造成采集的数据存在缺失、异常等质量问题，这些数据质量问题会导致错误的分析结果，影响电能质量治理决策效果.[1]

在上述数据问题中，以终端故障导致的数据缺失问题尤为突出，主要表现为一段时间内数据的完全缺失. 本文主要研究这一类缺失数据的自动填充问题. 现有学者多是利用单个指标数据特点，采用均值填充、自回归分析算法进行数据填充. 这些算法在缺失数据较多的情况下，准确性较低.

电网电能质量数据一个监测终端可以同时监测包括各次谐波在内的数千个指标，如果能够利用其它指标对当前缺失数据进行预测，有可能取得较好的填充效果.

为此，本文提出一种基于相关分析的缺失数据填充方法，首先使用归一化互信息计算所有与其采样周期一致的指标的相关性，找出其中相关性最强的指标，然后使用分段回归的方法建立指标数据回归模型，基于该模型预测缺失数据.

1 相关工作

1.1 缺失数据填充

缺失值填充常用的方法包括：1)使用描述统计值填充，如使用均值填充缺失数据. 这种方法会导致数据的随机性降低，损失了大量的数据信息. 在许多场合，均值填充是不适用的. 2)基于预测值的方法，如基于贝叶斯定理的缺失值填充方法，找到最大可能性的值来进行缺失值填充. 3)其他方法如多重插补法、ID3算法及其优化算法C4.5、热卡填充等.

电力领域相关的缺失数据填充方面，文献[2]提出一种运用光滑三次样条(Smoothing Cubic Spline)进行电力负载数据的缺失值填充，并且为了解决连续缺值情况下样条曲线不足以表示负载曲线细节的问题，将三次样条和反映负载曲线模式的值进行凸组合填充缺失值. 文献[3]根据等间隔有序的采样值模型推导出了一种基于正弦曲线的插值方法，效果较好，但是电网电能质量数据并不是等间隔有序的，不能使用正弦曲线的方法进行填充.

本文提出的电网电能质量缺失数据的填充方法，核心在于2个部分：一是相关分析，使用归一化互信息计算相关性;二是回归分析，分段回归建立预测模型.

1.2 相关分析

相关分析是求2个或2个以上处于同等地位的随机变量的相关关系. 通常使用皮尔森相关系数计算2个变量的相关性. 皮尔森相关系数无法度量非线性相关关系，为了度量非线性相关关系，引入互信息(Mutual Information). 互信息是2个随机变量能为彼此提供的信息量.[4]文献[5]将互信息用于航空故障检测数据的相关性分析，验证了互信息方法用于相关分析的可行性.

为了更好的对互信息进行量化，对其进行归一化，使值落在[0,1]，设置阈值来表示强相关性. 归一化互信息(Normalized Mutual Information，简称NMI)相关的成果表明了归一化互信息在计算相关方面有比较好的效果.[6]

1.3 回归分析

回归分析方法已广泛应用于电力领域. 文献[7]将回归分析应用到分析电气环境对公共低压电网的电能质量水平的影响中，对电能质量连续参数时间序列的长期趋势进行识别和量化. 文献[8]是时序数据，采用ARMA模型的方法填充缺失值，效果较好.

对于数据点较多的情况，只有1个回归方程有时候效果不够好，选择分段回归方式可以提高回归的准确性. 大部分情况下分段回归要求函数连续，本文对此不作要求，为了避免在同一个数据点2个分段的方程得到的结果差距较大，分段点的值为2个分段回归方程求得值的平均值.

2 基于相关分析的数据填充方法

给定电能质量监测指标的集合I,根据周期将应有数据量和实有数据量进行比较，得到存在缺失的指标的数据集.

1)对指标xi∈I，在集合I′=I-xi中，利用相关系数求得与xi同一采集周期中相关性最大的xj,i≠j.

根据2.1节的NMI(vi,vj)计算vi和vj的相关性. 并判断max{NMI(vi,vj),i≠j}是否大于阈值.

2)寻找最优拟合函数f，使得：f(vj)≈vi.

f包含常见的指数形式、对数形式、多项式以及分段函数形式等.

缺失数据填充的流程如图1所示，计算步骤如下：

1)使用2.1节中的相关分析方法，求出存在缺失值的指标x和其他指标的相关系数，找到相关性最大的指标y并判断相关系数是否大于所设阈值0.8，如果大于阈值，则进行第2)步；否则结束.

2)对监测值组成的数据集进行回归分析，得到拟合效果最好的回归预测模型.

3)使用2.2节中的回归分析步骤得到最优分段预测模型.

4)使用得到的分段拟合函数对缺失数据记录进行预测填充.

2.1 基于相关分析的变量选择

基于电网电能质量监测数据指标多的特点，在这些指标中可能存在着很强的相关性. 为了找出其中可能存在的相关关系，使用互信息作为相关性的度量.

归一化互信息定义式为：

其中I(X;Y)是互信息在联合集{X,Y}上的平均信息量.m和n分别是2个变量的取值个数.

I(X;Y)=E[I(xi;yj)]=

互信息的取值范围有以下结论：0≤I(X;Y)≤min{H(X),H(Y)}即互信息是非负的且以2个变量的熵的最小值为上界.

变量熵H(X)定义为：

对熵的定义式使用琴生不等式，可以得到互信息I(X;Y)满足：

0≤I(X;Y)≤min{log2m,log2n}.

可见，NMI∈[0,1]. 设置阈值用以判断相关性，本文将表示强相关的阈值设置为0.8.

2.2 基于回归分析的预测模型建立

对强相关的2个数据集进行多种形式的回归分析，得到效果最好的预测模型. 为了提高预测模型的准确性，使用分段回归的方式求解.

回归分析求预测模型步骤如下：

1)对于S个数据对(X1,Y1),(X2,Y2),…，(Xs,Ys)选择多种函数模型进行回归分析；

2)回归分析选择综合曲线回归和线性回归，选择其中回归效果最好的，使用实际值和拟合值的均方根误差R来比较回归效果，选择R最小的函数作为当前最优函数方程

3)采用自动分段的方法得到分段点，根据所得分段点分别进行回归分析，重复步骤2).

4)根据以上步骤得到各个分段的最优函数方程.

分段回归关键问题在于分段点的选取，为了解决根据经验选取分段点的不足，采用一种自动分段的方式选择分段点.

自动分段的目的是分段预测的数据集的均方根误差小于不分段回归预测结果，进一步使每个分段的均方根误差均小于不分段回归的均方根误差即可. 整个分段过程如图2所示.

自动分段步骤如下：

1)计算当前数据集的最优回归模型的均方根误差R;

2)取数据集前s个数据，求这s个数据的最优回归方程的均方根误差R1;取s+1个数据进行回归求均方根误差R2;如图3所示.

3)若R1R，则将第s个点视作分段点，通过分段点将数据集T分割成2个数据集T1和T2. 对于数据集T1和数据集T2，数据集T1视为一个分段，对数据集T2再次进行分段，若T2数据集的长度大于s+4,数据集T2重复步骤2)；否则令s=s+1，重复步骤2). 当s+4的值大于当前数据集长度时，分段结束.

3 实验验证

3.1 相关分析实验

电网电能质量监测数据是由监测点、监测指标、时间戳以及监测值组成的四元组数据. 一般情况下，一条数据记录的数据缺失会是四元组中某几个元素缺失，但是本文只关心整条数据记录的缺失情况，而不考虑缺失某几个元素的情况. 对于1条数据记录中的4个元素，监测点、监测指标以及时间戳根据其他数据记录可以得到准确值，电网电能质量监测数据的缺失实际上关注的是监测值的缺失与填充. 电网电能质量监测的原始数据集如图4所示.

为了计算指标之间的相关性，本次实验选取的数据是0303000981监测点2018年3月3日00:00—05:00共5个小时的国网电能质量监测数据. 在本次实验中，将所有指标的数据均视作存在缺失，并计算所有指标之间的相关性. 将NMI>0.8的值视作具有强相关性. 经计算，数据指标总数为2 555个，相关性强的指标为1 538个.

从具有强相关性的指标中选取一个指标进行回归实验，本文选取25次谐波电压相角这个指标作为存在缺失的指标，和其他指标计算归一化互信息的结果如表1所示，求得的NMI最大为1，

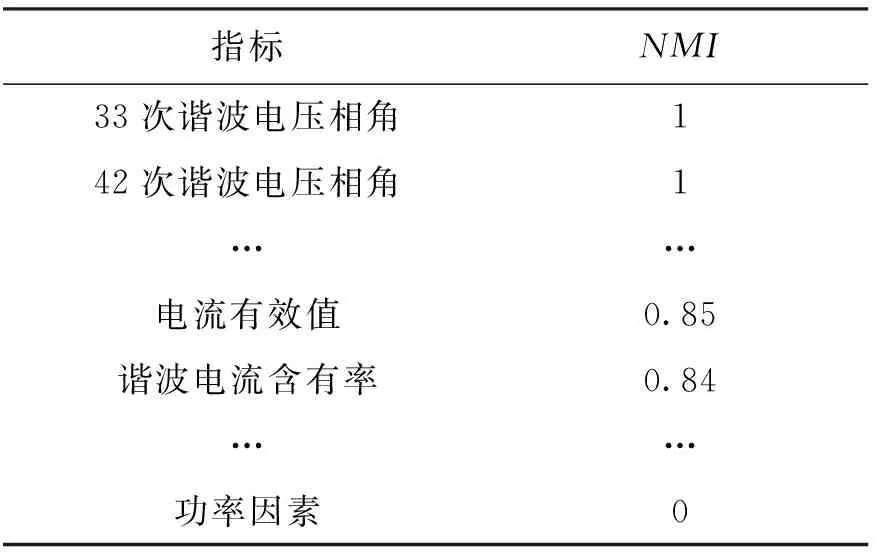
表1 归一化互信息计算结果

对应的指标为33次与42次谐波电压相角，本次实验选择33次谐波电压相角.

将这2个指标的监测值按照时间戳组成新的数据集T,形如表2所示.

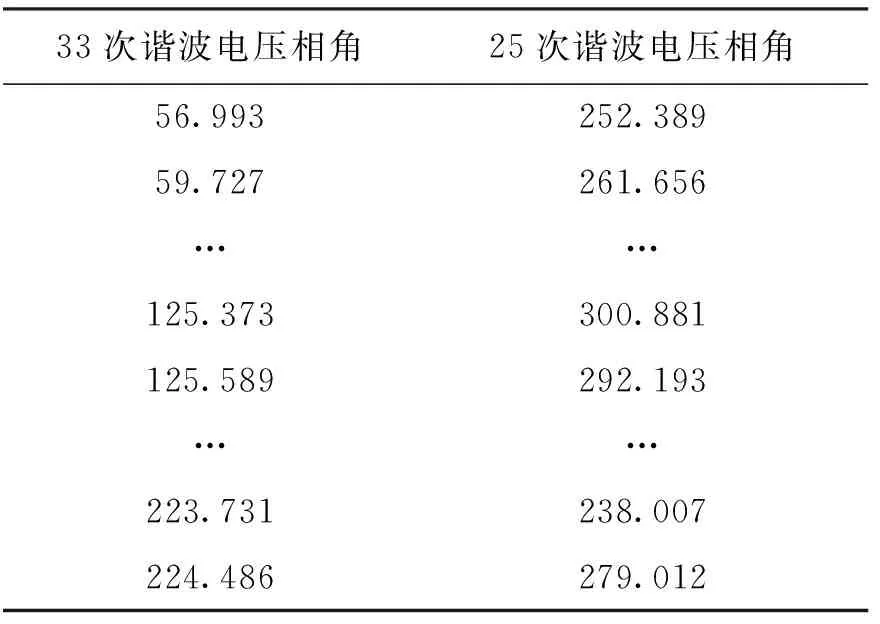
表2 相关指标数据

3.2 分段回归实验

为了比较本文采用的分段回归的填充效果，将其和不分段的回归分析、平均值填充几种方法的填充效果进行比较，采用的数据集为3.1节中得到的数据集T，数据集T中一共300个数据对，从中随机选取240对作为训练集，剩下60对作为测试集. 使用均方根误差(RMSE)和平均误差百分比(MAPE)比较回归效果.

(4)

其中yi是真实值，f(xi)是拟合值.

实验过程中多项式最高阶数的选择很重要，最高阶数过低容易导致欠拟合，最高阶数过高则容易产生过拟合. 在本文实验中，使用多项式进行曲线拟合的最高阶次分别选择为6次、10次以及20次，最终实验结果表明在电网电能质量数据的回归分析中，最高阶次选择10次效果较好，选择6次效果不如10次，选择20次会产生过拟合的情况.

自动分段时选择数据集的前s个数据，实验时s分别取{5,6,7,8,9,10}，比较s取不同值时拟合结果，s=7时均方根误差RMSE和MAPE最小，因此本文的s=7.

对训练集的数据分别进行平均值填充，分段回归和不分段回归求回归模型计算填充值，使用测试集中的数据评价训练集中得到回归模型. 连续时间的数据在数据集T重新排序之后随机分布在数据集中，随机抽取60对作为缺失数据，其他240对数据作为训练集，通过训练集得到缺失数据的预测模型. 图5为训练集数据拟合结果.

回归分析得到的函数方程是一个8次的多项式，使用分段回归的方式得到了7个分段点、8个回归方程，这8个方程能很好的反映数据集中的数据. 使用训练集计算之后得到的实验结果如表3所示.

结合训练集的图5及表3，可以看出，分段回归的预测模型比不进行分段的回归得到的预测模型更能反映出训练集中的数据，平均值填充不仅误差更大，而且完全无法反映出数据集中数据的特点，填充效果较之回归分析要差.

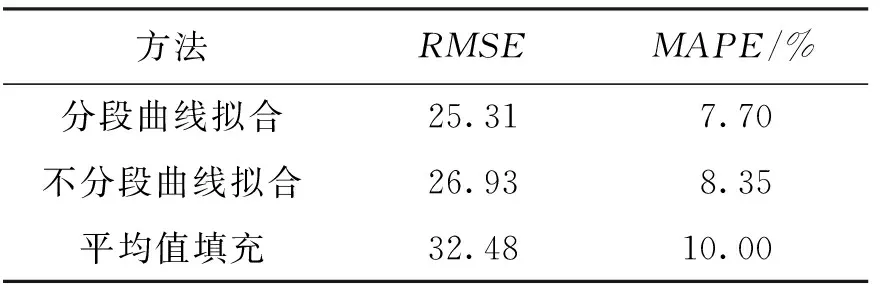
表3 训练集实验结果

测试集测试后，图6～7是测试集结果图.

表4是测试集数据在训练集数据得到的分段回归模型上进行测试得到的结果，可以看出，分段曲线拟合在测试集上的效果也是优于平均值填充的.

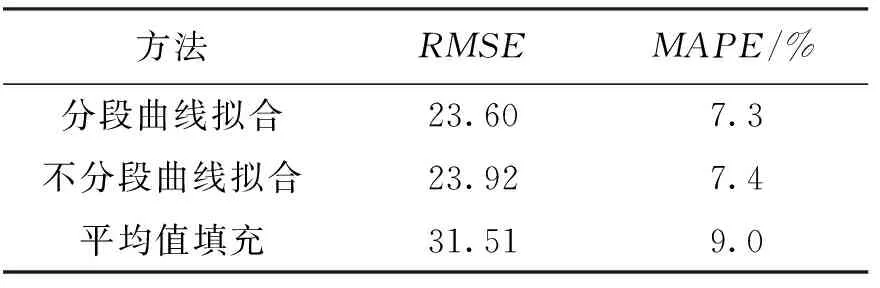
表4 测试集实验结果

可以看出，在缺失率为20%的情况下，测试集的结果和训练集得到的结果是一致的，数据误差比都在8%以下，平均误差百分比与平均值填充相比提高了20%，分段拟合并没有产生过拟合的情况，可以很好的拟合数据集. 同时无需数据本身的曲线模型，计算更加方便.

在缺失率10%、30%的情况下，基于相关分析的缺失值填充方法与平均值填充方法比较结果如表5～6所示.

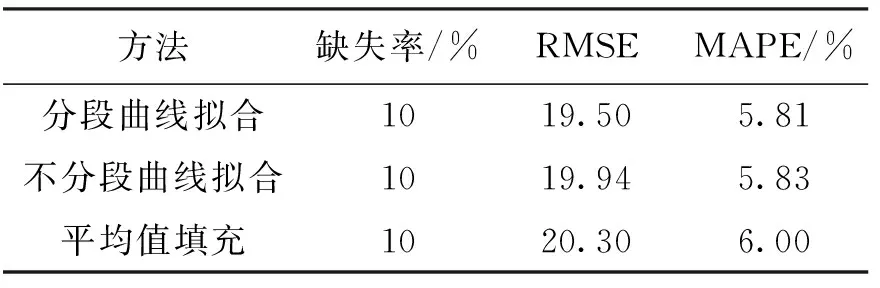
表5 缺失率10%实验结果

综合不同缺失率下填充准确性的比较，可以看到，在缺失率小于20%的情况下，使用分段曲线拟合效果更好；缺失率达到30%,分段曲线拟合误差比缺失值填充效果更差，此时选择不分段的效果更佳.

4 结语

本文根据实际的数据特点，采用相关分析的方式得到具有相关关系的2个变量，然后对得到的1组变量的数据点进行分段曲线拟合，得到1个分段的函数方程，使用得到的函数方程来对缺失数据进行预测. 分段函数采用最高次项为10次的多项式以及指对数函数结合的曲线拟合，避免过多次项导致的过拟合现象，同时具有较好的拟合效果. 实验证明了曲线拟合得到的填充值具有更高的准确度，误差在10%左右. 这种方法准确度较高，但是相对的运行效率较低，接下来工作将主要研究这种方法的优化以提高运行效率.