稀疏二分类数据贝叶斯Meta分析方法及实现

张天嵩

Meta分析可以定量、科学地合成研究结果，已在许多科学领域取得革命性的成果，有助于建立循证实践、解决相互矛盾的研究结果问题[1]。众多医学Meta分析中涉及稀疏二分类数据的现象十分常见，即感兴趣的测量结局(如某种干预措施的不良事件)为二分类数据且十分稀疏，特别是在纳入Meta分析的单个研究中有1个或2个臂的事件发生数为0(分别称为“单零研究”或 “双零研究”)，一项对500项Cochrane系统评价随机抽样调查的研究表明，有30%的系统评价中至少有1个研究1个臂的事件发生数为0[2]。经典的Meta分析方法不适用于稀疏数据(sparse data)，特别是纳入Meta分析中含有多个单零研究或双零研究时，在数据分析方法学方面面临着众多挑战，已引起国内外研究者的关注，相继提出多种模型和方法[3-6]。本文介绍二项式-正态层次模型(BNHM)和贝塔-二项式模型(BBM)，以及基于这两种模型框架下的贝叶斯Meta分析方法，并通过实例来介绍软件实现过程。

1 方法

1.1 研究数据 数据来源于1项Cochrane系统评价[7]，其主要观察长效β2受体拮抗剂(LABA)合用糖皮质激素吸入剂(ICS)对儿童慢性哮喘的干预作用，对照组为单纯应用ICS。本文选取测量结局为严重不良事件且FEV1平均基线值≥ 80% 预计值亚组的数据，共纳入13个研究，其中含有3个单零研究、4个双零研究，表1显示，数据中变量名study、rtrt、ntrt、rctrl、nctrl分别表示研究名称、治疗组事件发生人数和总人数、对照组事件发生人数和总人数。

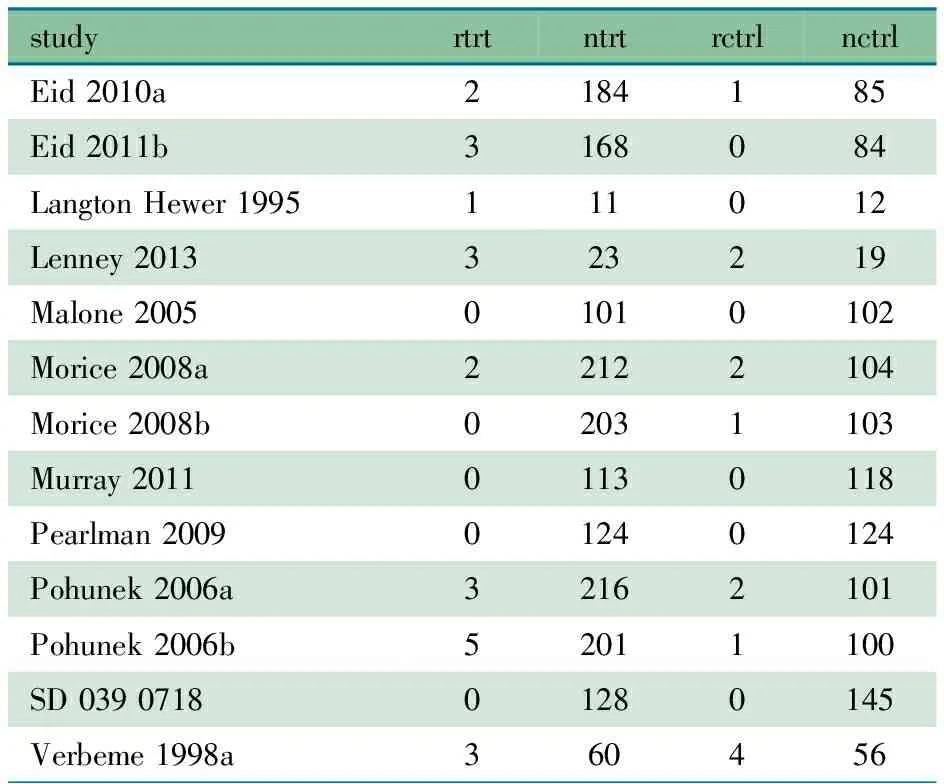
表1 分析数据

1.2 模型与方法

1.2.1 BNHM 针对二分类数据，经典Meta分析基于异质性假设可分为固定效应和随机效应2种模型，随机效应采用正态-正态层次模型(NNHM)最为流行[8],但在某些情况下，该模型假设难以成立，因此，更多的研究者建议采用BNHM。模拟研究表明，在大多数情况下，BNHM表现优于NNHM，可以获得无偏倚点估计及合适的置信区间[4，9]。本文采用的模型由Smith等提出[10]：假设纳入Meta分析第i(i=1,2,...,N)个研究第k(k=0,1)个臂的事件发生人数和总人数分别为rik和nik，每个臂的事件发生率为pik，则有：

rik～Bin(pik,nik)

logit(pik)=μi+θixik

θi～N(θ,τ2)

模型中，μi表示第i个研究中事件发生的基线风险，是比值(odds)的对数尺度，可视为经典logistic回归的截距参数，为固定效应；θ表示平均干预效应，是比值比(OR)的对数尺度；τ2表示研究间干预效应异质性；xik为干预指示器，如果干预为治疗组(k=1)则其为+0.5，如果干预为对照组(k=0)则其为-0.5。可以发现，实际上BNHM为广义线性混合效应模型(GLMMs)家族中的一员，不依赖于正态近似，可以对二项式数直接建模，非常灵活。

1.2.2 BBM 针对二分类数据Meta分析的BBM，是真正的随机效应模型(REM)，实质是两步(two-stage)回归模型[11，12]。

假设纳入Meta分析第i(i=1,2,...,N)个研究第k(k=0,1)个臂的事件发生人数和总人数分别为rik和nik，每个臂的事件发生率为pik，则rik服从带有3参数(n,α,β)贝塔-二项式分布(第一阶段)：rik～Bin(pik,nik)，pik～Beta(αk,βk)，其中贝塔分布的均数为μk=αk∕(αk+βk)，可知期望E(rik)=nikμk，相应方差为Var(rik)=nikμk(1-μk)[nik+αk+βk)∕(αk+βk+1)]，假定所有研究中治疗组和对照组相关系数均相等，均为ρ=1∕(αk+βk+1)。

第二阶段，Meta分析模型为：g(g)=b0+θxk。式中，g(g)为广义线性模型家族常用的连接函数，根据效应量不同选择不同连接函数。如效应量为OR，则采用logit连接函数；如效应量为RR，则采用对数连接函数。θ表示平均干预效应；xt为干预指示器，xt=0表示干预为对照组，xt=1表示干预为治疗组。

因该模型所具有的闭型对数似然函数有利于参数估计，可以比较轻松地在频率学框架或贝叶斯框架的软件实现，如前者可以采用SAS软件的NLMIXED程序实现[11]，后者可以采用R软件的MetaStan包实现。

1.3 模型拟合 本文采用完全贝叶斯策略拟合BNHM(Smith模型)[10]，需要对μi、θ、τ的3个参数指定先验分布。对于μi指定为无信息先验分布N(0,102)[13]，对于θ分别指定为无信息先验分布N(0,1002)[14]及弱信息先验分布N(0,2.822)[15]，对于τ分别指定为均匀分布uniform(0,5)[14]、半正态分布HN(0.5)[15,16]及半柯西分布HC(0.5)等，共6种模型组合，具体如表2所示。

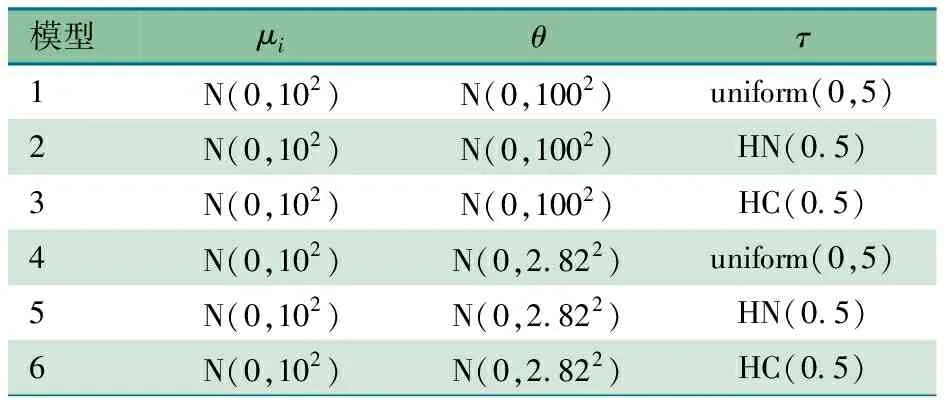
表2 不同参数的先验分布设定

BNHM和BBM均通过R软件(ver3.4.4)的MetaStan扩展包(ver0.1.0)[17]拟合进行贝叶斯Meta分析，迭代50 000次，前20 000次用于退火以消除初始值的影响；采用收缩因子(shrink factor)进行收敛性判断，如果每个参数的收缩因子接近于1，则认为是马尔可夫链收敛[18]。具体代码及简要解释见表3和表4。

表3 基于BNHM稀疏二分类数据贝叶斯Meta分析方法代码(R软件)及简要解释

表4 基于BBM稀疏二分类数据贝叶斯Meta分析方法代码(R软件)及简要解释

2 结果

2.1 BNHM拟合结果 基于贝叶斯分析框架下，拟合BNHM主要结果如表5所示，其中3个参数的收缩因子(结果中Rhat值显示)均为1，表明马尔可夫链已收敛；基于BNHM框架，对参数μi、θ、τ指定相应的先验分布，拟合不同的模型结果如表2所示。可以发现，不同模型中最主要的2个参数干预效应参数θ和异质性参数τ的后验均数及95%CI十分相近，但将τ指定为均匀分布时获得的后验均数估计值较其他先验分布更大且95%CI更宽。

2.2 BBM拟合结果 基于贝叶斯分析框架下，拟合BBM主要结果如表6所示，模型中9个参数的收缩因子(结果中Rhat值显示)均为1，表明马尔可夫链已收敛。主要感兴趣的参数是平均干预效应θ(lnOR)，后验分布均数点估计及95%CI为0.12(-0.83，1.09)，返回OR及其95%CI为1.13(0.44，2.97)。

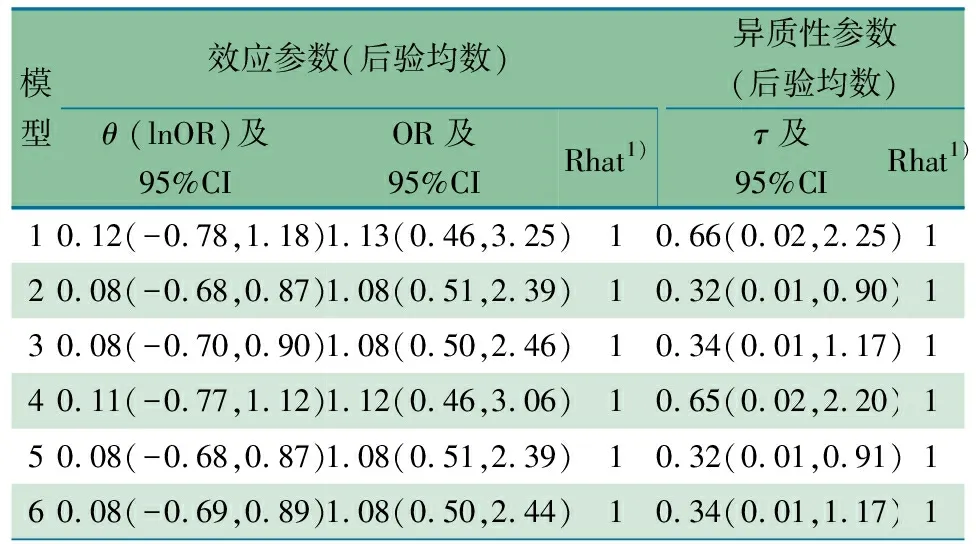
表5 基于不同先验分布稀疏二分类数据贝叶斯Meta分析结果

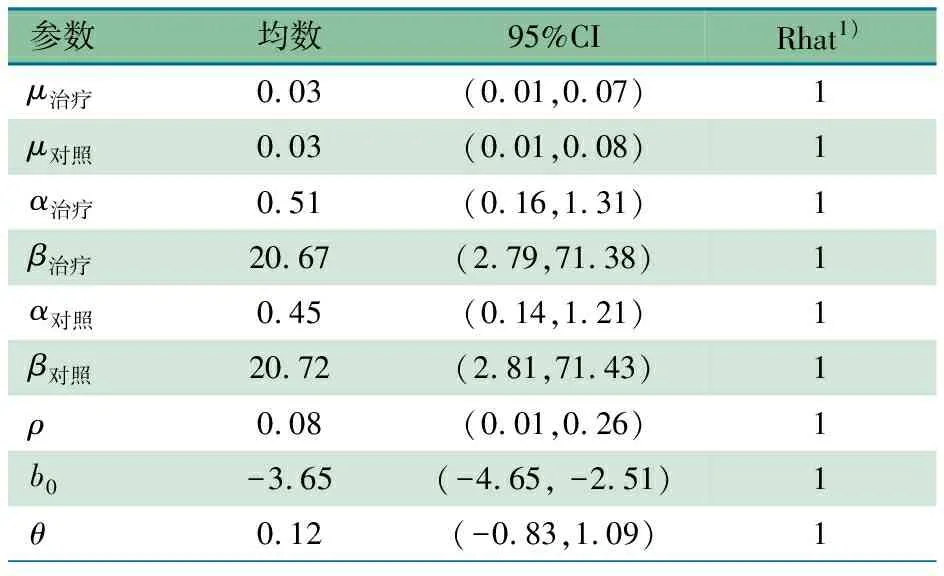
表6 拟合BBM主要参数的后验分布结果

3 讨论

在医学领域内，虽然将发生概率<1/1 000的事件肯定为稀有事件，但更多的是将发生概率< 1/100定义为“稀有”[5，6]，如观察某些药物少见或罕见的不良反应，此类数据称为稀疏数据或稀有数据(rare data)。对于稀有事件，单个研究结果通常不足以发现不同干预措施效果的差异，而 Meta 分析则可以通过汇总来自多个临床试验的数据，增加样本量和统计效能，可能是获得证据的唯一方法[6]，但经典Meta分析方法学并不一定适用于稀疏数据，需要进一步探索和研究相关的分析方法。

目前常用于稀疏二分类数据Meta分析的方法主要有Peto法(Peto's method)、Mantel-Haenszel法、干预臂连续校正(treatment-arm continuity correction)法、Logistic 回归、贝叶斯Meta分析、BBM等，并有文献就相关方法进行了优劣比较，有兴趣的读者可以研读相关文献[5]。简而言之，经典方法(如Peto法、Mantel-Haenszel法等)和通用Meta分析软件一般是对单零研究进行连续性校正(如对四格表数据每格的数据各加0.5)，而将双零研究排除在外，不进行合并；Logistic 回归虽然不需要对单零研究进行连续性校正，但也会将双零研究除外，不纳入分析。这些处理方法存在的主要问题有[4，5]：①采用“连续性校正”对零事件进行修正，对稀疏数据的 Meta 分析会造成结果偏倚；②忽略了双零研究通过样本量而提供的相关信息；③双零研究不纳入分析可能不符合“伦理”。

贝叶斯统计学和经典统计学是当前两大主要统计学学派，Meta分析也主要有频率学和贝叶斯两大策略，尤其是贝叶斯策略，随着现代计算机技术的出现和发展，特别是马尔可夫链蒙特卡洛(MCMC)方法的建立，成功解决了高维积分运算等制约贝叶斯统计发展问题，近年来在Meta分析特别是处理复杂或特殊数据如稀疏数据时应用越来越广泛。针对二分类数据，贝叶斯策略主要有NNHM和BHNM两种建模框架，后者更为合适[19]。基于BHNM框架下有多个随机效应模型，模拟研究表明以Smith模型为优[10，20]。贝叶斯统计方法综合未知参数的总体信息、样本信息及先验信息，根据贝叶斯定理，获得未知参数的后验分布，进而对未知参数进行统计推断，在实践中对先验信息的利用和指定非常重要。在BHNM框架下，Smith模型中[10]不同参数的先验分布可以允许利用先验信息确定，本研究参考既往文献，一般将基线风险参数μi指定为无信息先验正态分布N(0,102)[13]。对干预效应参数θ一般可指定为无信息先验(non-informative prior)，如均数为0、具有很大方差的正态分布N(0,1002)[14]；也有研究者基于Cochrane系统评价计算出1个弱信息先验(WIP)，如均数为0、方差约为8的正态分布N(0,2.822)[15]。对于异质性参数τ一般指定为均匀分布uniform(0,5)[14]，但基于此的先验信息获得的τ后验均数较大、95%CI更宽；鉴于τ值为0.25、 0.5、1和 2分别表示异质性中等、较大、大、很大，而模拟结果显示半正态分布HN(0.5)获得的τ后验均数与众多Meta分析结果更为常见与接近，所以HN(0.5)是一个非常好的先验选择[15,16]，而半柯西分布HC(0.5)则可以作为敏感性分析，这些参数的先验设定对今后稀疏二分类数据Meta分析实践具有一定的指导意义。

BNHM、BBM等几种新的模型和方法为合并稀疏二分类数据提供了更为合理的分析策略。一项模型研究表明[11]，测量结局为稀疏事件的Meta分析，在干预效应估计偏倚和准确性方面，BBM较其他模型为优。实际上，BNHM和BBM均为两阶段REM，但对分布假设有异同，对事件两种模型均假定服从二项式分布，而对事件概率前者认为服从正态分布(经数据转换)，后者认为服从贝塔分布，正因为两种模型对随机效应的分布假设不同，所合并的结果有可能会有差异。在BBM框架下，可以选择OR、危险比(RR)以及危险差(RD)等作为干预效应量，而Bakbergenuly等[21]建议BBM采用OR为干预效应量。

BNHM和BBM等模型均可以通过WinBUGS、OpenBUGS、JAGS、Stan等贝叶斯软件包来实现，但需要系统评价员编写相关代码，以及设定不同马尔科夫链的初始值设定等，而且应用MCMC方法等均需要具备一定的专业知识(如收敛性诊断)和实践经验等，这对于非统计学专业人员而言有一定的难度。有鉴于此，Günhan 编写的MetaStan包，可以通过R软件调用Stan软件，从而避免编写Stan软件实现模型代码(较R软件代码编写难度更高)，轻松地拟合BNHM及BBM等模型而获得相应的结果。此外，收敛性诊断是MCMC算法非常重要的问题[22]，MetaStan包主要采用的是收缩因子法，在实践中，还可以与shinystan包联用，通过绘制和观察Gibbs动态抽样图、迭代历史图、抽样自相关图，以及参数后验分布的核密度估计图等，判断马尔可夫链是否收敛[10]，鉴于篇幅，本研究不再展示，有兴趣的读者可以自行研究和运用。

基于以下优点，针对稀疏二分类数据进行Meta分析，推荐使用基于BNHM和BBM等模型框架下的贝叶斯方法：①建模灵活，并在贝叶斯分析软件中可实现性强，如采用R软件的MetaStan包可以轻松拟合BNHM和BBM；②充分考虑了模型中参数如方差等的不确定性，合并效应量点估计及95%CI来源于参数的后验分布，结果可靠；③二项式似然可以直接对稀疏数据，特别是单零和双零研究数据直接建模，不需要对数据进行连续性校正，降低了经典Meta分析因采用连续性校正造成的偏倚。

值得注意的是，虽然目前有众多的稀疏二分类数据Meta分析模型和方法，但尚无定论明确回答哪种方法是最佳的稀疏数据Meta分析策略，不同的方法基于不同的假说，其效度难以评估。因此，系统评价员在制定系统评价/Meta分析计划时就要考虑到，如果遇到稀疏数据时，应选择多种分析方法进行敏感性分析，以确定结果是否稳健。