基于前景理论和VIKOR法的空战威胁评估

胡 涛，王 栋，黄震宇，孙 曜，姜龙亭,2

(1.空军工程大学航空工程学院，西安，710038；2.95974部队，河北沧州，061000)

合理评估敌机威胁大小并排序，是进行目标分配和机动决策的前提条件[1]。但是，不同的决策者依赖于自身专业知识，使得威胁评估结果各异。

传统的随机决策理论认为决策者可以完全获取决策问题信息且决策者处于完全理性的状态[2]。而前景理论认为，外界的复杂环境会对决策者的个人偏好产生重要影响[3]，因此采用价值函数和权重函数代替随机决策理论中的效用函数和概率函数[4]，可考虑评价对象的不确定性，并且可以反映决策者的主观偏好和风险态度[5-6]，使得决策过程更加符合空战实际环境和飞行员心理行为。

基于上述分析，本文提出一种基于三参考点前景理论和VIKOR法的空战威胁评估模型。首先引入前景理论来体现飞行员偏好的不确定性；针对主观赋权法依赖专家知识的缺陷，考虑各方案间的独立性，建立评估方案集前景价值最大化规划模型求解指标权重；为了克服仅采用指标平均值作为参考点的局限性，避免单参考点带来的信息损失和决策结果分辨率下降的问题，参考TOPSIS理论[7]，引入正负理想点作为另外2个参考点；最后，综合考虑群体价值和个体遗憾并反映决策者偏好，采用VIKOR法对目标进行威胁排序，使得评估结果更加符合决策者认知，符合空战实际情况。

1 前景理论简介

前景理论考虑了复杂环境下的决策者心理特征，通过引入价值函数和权重函数代替传统随机决策理论中的效用函数和概率函数，将决策期望转化为前景价值[8]。当前景价值为收益时，决策者更倾向于风险规避，而当前景价值为损失时，决策者更倾向于风险偏好[9]。同时认为决策者对待同等损失和收益时，对损失更为敏感。决策问题的收益和损失取决于参考点的选择[10]，体现了决策者的不同偏好。

在前景理论中，前景价值由价值函数v(·)和决策权重函数π(·)共同决定。

Vij=∑v(xij)π(p)

(1)

式中：Vij为方案Ai在指标Cj下的前景价值；v(xij)为价值函数，以参考点作为基准，表征在实际情况下决策者的收入和损失主观价值[3]；π(p)为决策权重函数，表征决策者对于执行方案可能得到的收益或损失的心理预期。

价值函数的表达式为：

(2)

式中：xij表示决策者所获得的价值，xij≥0时，说明决策者获得收益，xij<0时，说明决策者遭受损失；α和β分别表征在遭受收益和损失时价值函数的发展趋势，体现决策者的重视程度，0<α,β<1，当α=；β=1时，表示决策者对风险保持中立态度；λ表示损失规避系数，λ>1时表示面临相同的收益和损失时，决策者对于损失更敏感。

权重函数的表达式为：

(3)

式中：π+(p)和π-(p)分别表示决策者对收益和损失的决策权重函数；p为指标概率，θ和μ分别为决策者的收益偏好程度和损失规避程度。

根据文献[11]，一般取α=β=0.88、λ=2.25、θ=0.61、μ=0.69。

2 指标体系的建立和权重确定

2.1 威胁评估指标体系的建立

在空战对抗中，敌我双方的能力参数和态势信息是进行威胁评估的重要依据，根据系统效用理论可知，评估指标应当具有完备性、独立性和最小性等特点[12]。因此威胁评估指标体系应既包括空战能力威胁评估，又包括空战态势因素威胁评估，见图1。

图1 威胁评估指标体系

2.1.1 空战能力威胁评估

根据文献[13]，构建单机空战能力威胁模型：

C=

[lnB+ln(1+∑A1)+ln(1+∑A2)]ε1ε2ε3ε4

(4)

式中：C为战机的空战能力；B为机动能力；A1为火力能力；A2为探测能力；ε1为生存能力；ε2为操纵能力；ε3为航程能力；ε4为电子对抗能力。

2.1.2 空战态势因素威胁评估

在中远距空战中，主要考虑双方的相对角度、飞行速度和相对距离[14]，空战态势几何关系见图2。

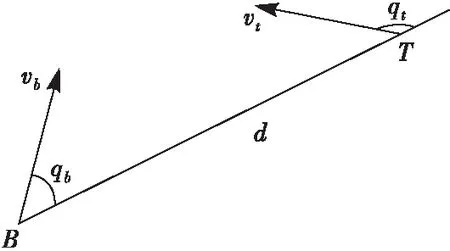
图2 空战态势示意图

图中B为我机，T为敌机；d为我机与敌机之间的距离；vb、vt分别为我机和敌机的速度；qb为我机航向与目标线夹角，qt为敌机航向与目标线夹角。设dm为我机导弹最大攻击距离，dmt为敌机导弹最大攻击距离，dr为我机探测设备最大跟踪距离，分别定义角度威胁指数Ta、速度威胁指数Tv、距离威胁指数Td如下：

(5)

(6)

(7)

2.2 决策矩阵规范化

假设多属性决策问题有评估方案集Ai(i=1,2,…,m)，评估指标Cj(j=1,2,…,n)，则m个评价方案对n个评价指标的评价矩阵为Y=[yij]m×n。

由于所选的评价指标类型和量纲各不相同，导致数据无法直接拿来比较，为了消除不可比性，需要对指标值进行规范化处理，得到规范化评估矩阵X=[xij]m×n。规范化处理方法如下：

效益型指标：

(8)

成本型指标：

(9)

固定型指标：

(10)

式中：δj为固定型指标uj的最佳取值。

2.3 指标权重计算

(11)

(12)

根据拉格朗日乘数法对上述规划模型进行求解，引入参数δ，有：

(13)

对ωj和δ分别求偏导并令其为0，有：

(14)

则可以得到各评估指标权重计算公式为：

(15)

(16)

3 基于前景理论和VIKOR法的决策模型

3.1 选择参考点

在前景理论中，单纯以各指标平均值作为参考点存在诸多局限[15]，因此参考TOPSIS理论，引入正负理想点作为另外2个参考点，从而避免信息丢失和决策结果分辨率的下降。

实际空战过程中飞行员的偏好在很大程度是模糊的，于是本文采用模糊分析法[16]来确定偏好权重。

首先根据决策者对不同参考点的偏好程度，基于式(17)建立模糊矩阵P=[pij]s×s，然后对P进行一致化处理，根据式(18)～(19)得到模糊一致矩阵Q=[qij]s×s；再根据式(20)～(21)确立各偏好权重为L=(l1,l2,…,ls)。

(17)

(18)

(19)

(20)

(21)

3.2 VIKOR排序法

VIKOR法是一种多准则决策方法，同时考虑最大化群体效益和最小化个体遗憾[17]，可以平衡群体和个体之间的关系。相比TOPSIS法，VIKOR法得到的最好方案是带有优先级的折衷方案，最接近理想方案[18]。

结合前景理论，VIKOR法的具体步骤如下：

1)确定综合前景价值矩阵的正理想解f+和负理想解f-：

(22)

(23)

2)计算评估方案的群体效益值Si和个体遗憾度Ri：

(24)

(25)

3)计算评估方案的折衷排序值Qi：

(26)

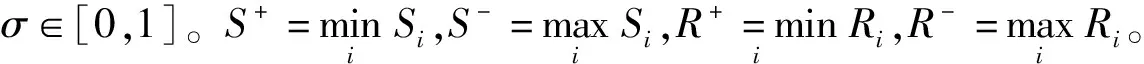
4)根据Si、Ri和Qi的值对评估方案进行排序。Qi的值越小，代表目标的威胁程度越大，即方案越优。

3.3 基于前景理论和VIKOR法模型的评估步骤

1)根据式(4)～(7)建立评估矩阵，并根据式(8)～(10)对评估矩阵进行规范化处理，得到规范化的评估矩阵X。

2)根据式(1)～(3)确定基于3个参照点的评估方案Ai在指标Cj下的前景价值，得到前景价值矩阵Vh(h=1,2,3)。

3)根据式(17)～(21)计算决策者对3个参考点的偏好权重L=(l1,l2,l3)，分别对其前景价值矩阵Vh(h=1,2,3)进行加权求和，得到各方案Ai在各指标Cj下的综合前景价值矩阵V。

4)根据式(11)～(16)确定评估指标权重W=(ω1,ω2,…,ωn)。

5)根据指标权重W和综合前景价值矩阵V，采用VIKOR法对评估方案进行威胁排序。

4 仿真验证

假设我机在空战中遭遇敌方6架飞机(F-16C,F-15E,F-5E各2架)，由式(4)确定敌机空战能力分别为16.8、19.8和9。敌机在我机火控雷达探测范围内，我机速度为320 m/s，导弹最大射程为60 km，雷达的最大探测距离为120 km。空战态势如表1所示。

表1 空战态势信息

根据式(4)～(10)，可得规范化目标属性矩阵X：

根据式(1)～(3)确定各参考点前景价值矩阵Vh(h=1,2,3)：

根据式(17)～(21)计算决策者对3个参考点的偏好权重L：

加权求和得到综合前景价值矩阵V:

根据式(11)～(16)确定评估指标权重W：

根据综合前景价值矩阵V和指标权重W，根据VIKOR法得到排序结果，如表2所示。

表2 σ=0.5时三参考点下决策结果

根据表2～5，得到当σ=0.5时，基于三参考点和其他3种单参考点决策结果的一个综合对比，如表6和图3。

表3 σ=0.5时指标平均值参考点下决策结果

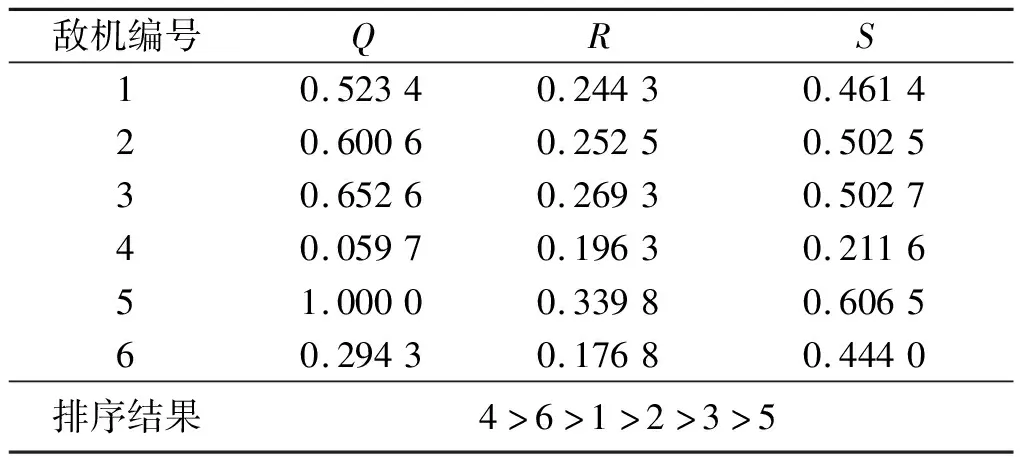
表4 σ=0.5时正理想点参考点下决策结果

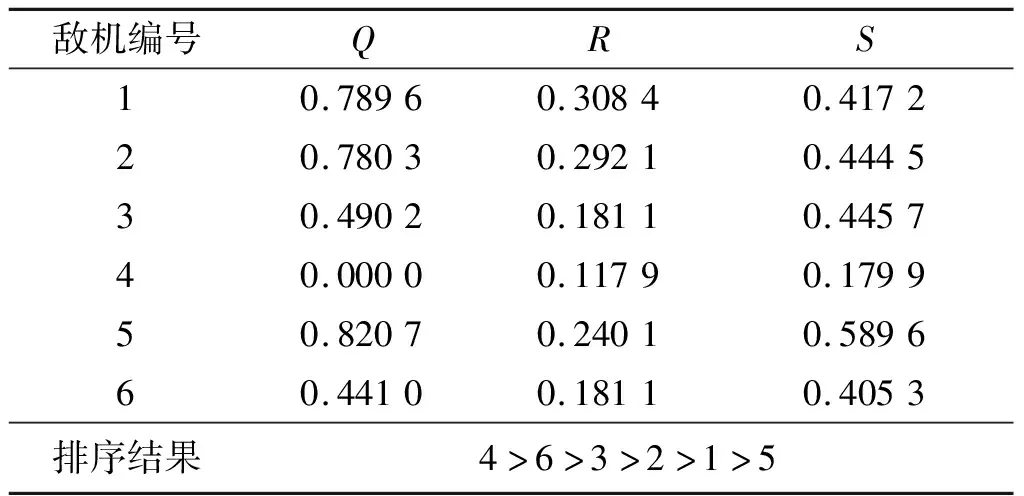
表5 σ=0.5时负理想点参考点下决策结果

表6 σ=0.5时4种参考点下决策结果对比

图3 4种参考点下目标威胁大小对比

从表6和图3可以看出，本文所提的三参考点决策模型和其他单参考点决策模型具有相似的发展趋势，且威胁评估排序结果基本一致，这反映了三参考点决策模型的稳定性。

同时，从威胁排序结果来看，目标4和目标6的威胁较大，其中目标4的威胁最大，在各种参考点情况下威胁排序都是第一；而目标2和目标5的威胁较小。本文提出的三参考点决策模型和其他参考点模型结果存在差异，主要是因为：

1)相比单参考点模型，三参考点决策模型能够充分体现决策者偏好，并从数据的整体分布趋势出发，考虑正负理想点等低概率事件，从而避免了单参考点导致的决策信息损失和决策结果分辨率下降等问题。

2)VIKOR法在决策过程中没有考虑决策者的偏好变动，导致实际中由于决策者对个体遗憾和群体价值的偏好不同而使决策结果产生变动，而三参考点决策模型在构建过程中就充分考虑了决策者偏好变动。

为了更好体现三参考点决策模型相比单参考点决策模型在评估目标威胁区分度方面的优越性，将4种情形下得到的折衷排序值按照从小到大的顺序分别进行排列，再将顺序折衷排序值两两相邻作差，得到顺序折衷排序值差值，并取折衷系数σ=0.25、0.5、0.75，结果见图4和表7，算法编号1～4分别代表三参考点、指标平均值参考点、正理想点参考点、负理想点参考点决策模型。

从图4和表7可知，本文所提的三参考点决策模型在计算折衷排序值时，顺序最小折衷排序值差值的数值最大，顺序折衷排序值均值的数值最大，能够更好体现目标威胁区分度，对目标威胁进行合理评估及排序。

图4 4种参考点下顺序多准则折衷排序值差值

表7 4种参考点下目标威胁区分度比较

4.2 灵敏度分析

为了分析折衷系数σ在考虑群体价值和个体遗憾时对威胁评估结果的影响，将σ∈[0,1]以0.1为间隔，取11次值，通过各参考点决策模型得到威胁评估结果进行比较，其中排序等级1～6表示6个目标威胁由最大到最小，结果见图5。

图5 不同折衷系数下的目标威胁排序

由图5可知，在不同的折衷系数σ下，基于三参考点决策模型的6个目标威胁排序值基本没有发生变化，只有当σ=0.1和0.2时，目标6的威胁超过了目标4；当σ≥0.2，目标4的威胁超过了目标6；基于正理想点参考点的决策结果变化不大，其结果变化幅度超过了三参考点决策模型；而基于指标平均值参考点和负理想点参考点的目标威胁排序结果发生较大偏差。出现上述现象是因为在考虑不同的折衷系数σ时，决策者对于群体和个体的偏好不同，评估结果自然会存在一定的区别。而三参考点决策模型能够充分体现决策者对于个体和群体的偏好差异，在模型的构建过程中就予以充分考虑，因此模型稳定性较强。

5 结论

针对当前复杂环境下空战威胁评估未考虑决策者的认知局限和决策偏好受个人知识背景的影响，以及没有综合权衡单个目标和目标群体之间的威胁大小的问题，构建基于三参考点的前景理论和VIKOR法的威胁评估模型，通过仿真验证，可以得出以下结论：

1)采用基于三参考点的前景理论决策模型能够减少由于单一参考点产生的决策信息损失和决策结果分辨率下降的问题，决策结果区分度更大。

2)基于前景理论的VIKOR法决策模型，能够克服传统VIKOR法没有考虑决策者偏好变动的局限，使得决策更加合理，决策结果稳定性更好。采用VIKOR法进行目标威胁排序，能够综合考虑个体遗憾和群体价值，使得威胁排序更加合理。

3)在实际空战中，参考点的选择也与双方的作战意图相关，下一步需要研究双方作战意图对参考点选取的影响，并针对参数取值进行研究。