地下水污染强度反演识别的SCE-UA算法
王 敬,韩 忠,梁 浩,刘乐军,林艳竹,袁星芳
(1.山东省第六地质矿产勘查院,山东 威海 264209;2.山东省地质环境监测总站,济南 250014;3.中国地质环境监测院(地质灾害技术指导中心),北京 100081)
0 引 言
地下水是非常重要的饮用水源[1]。随着经济的快速发展,我国地下水污染问题已经非常严重[2]。在地下水污染发生后,如何准确、快速通过监测点污染物浓度识别出污染源排放强度及其动态变化就变得极为重要。此类问题属于地下水污染反演识别问题,并已经成为地下水科研领域一个非常重要的研究方向[3]。
面对这一问题,过去几十年间国内外水文地质学家探讨了各种方法来进行地下水污染源反演识别:Wagner开发了一种可以同时反演水文地质参数和污染源特性的非线性极大似然优化算法[4];Alapati等设计了一种基于最小二乘法的一维地下水污染源反演方法[5];Foddis等利用人工神经网络(ANNs)算法对二维含水层进行了污染源反演识别[6];Jha等采用自适应模拟退火算法进行了地下水污染源特征的反演[7];Machiwal 结合多元统计分析方法和基于GIS的地质模型,进行地下水污染的识别[8]。在国内,江思珉等采用和声搜索算法[9]、单纯型模拟退火算法[10]和Hooke-Jeeves吸引扩散粒子群混合算法[11]等,进行地下水污染源相关特性的反演识别;顾文龙等利用改进的MCMC方法与贝叶斯推理进行地下水污染源释放历史反演[12];肖传宁等开发了一种基于径向基函数模型的地下水污染反演优化模型[13]。然而,由于地下水含水层的复杂性、地下水溶质运移的非线性及人类活动影响等问题的存在,导致设计一种高效且可行的地下水污染源反演模型并非易事,如前面提到的各种优化算法均或多或少存在一些弊端:局部寻优算法(最小二乘法和线性规划法等)往往由于容易陷入局部最优解,而无法获得全局最优解;全局寻优算法(遗传算法、模拟退化算法等)能够处理不连续和不可微的方程,并且能够寻找到全局最优解,但此类方法往往涉及到反复的模型调用,并且求解效率会随着数值模型复杂程度的增大而降低[14]。
基于以上分析,亟待提出一种能够高效获得全局最优解的地下水污染源反演优化算法。由Duan等提出的SCE-UA算法结合了随机搜索、生物竞争进化和单纯型法等方法的优点,是一种可以快速、有效、一致地搜索到全局最优解的进化算法[15]。Kuczera等分别比较了SCE-UA算法、MSX算法(拟牛顿法和单纯型法)和遗传算法在进行地表水模型参数反演识别中的搜索效率,结果证明SCE-UA算法收敛效果更好、鲁棒性更强[16]。然而,在利用SCE-UA算法进行水文地质参数反演,特别是地下水污染强度及其动态变化反演方面的应用还很少。为此,开发了一个耦合SCE-UA优化算法、地下水水流和溶质模型,适用于多污染源稳定流和非稳定流、定浓度和不定浓度排放等各种复杂条件下地下水污染源反演识别的优化模型,并进行了不同案例情况下的反演验证。
1 研究方法
1.1 SCE-UA优化算法
最初由美国亚利桑那大学的Duan等在1992年进行降雨径流模型参数优化问题时提出的SCE-UA算法是一种全局优化算法[17]。该算法能够有效处理含水层各向异性及地下水溶质运移强烈非线性所带来的容易停留在局部最优解、早熟收敛等弊端,可以高效、快速搜索到全局最优解,且相较其他类似优化算法效率更高、鲁棒性更强。SCE-UA算法综合了随机搜索、生物竞争进化和单纯型法等方法的优点,引入了种群的概念,在可行域内随机生成复合型点,并依据生物进化规则不断进行优化。
SCE-UA算法的具体实现步骤如下:
(1)算法初始化。设定维数n,参与进化的复合型p个(p≥1)和每个复合型包含的顶点数目为m(m≥n+1),计算样本点数目s=pm。
(2)产生样本点。在可行域内随机产生s个样本点x1,…,xs,分别计算每一点xi处的目标函数值fi。
(3)样本点排序。把生成的s个样本点按目标函数值f升序排列。
(4)划分复合型群体。将s个样本点划分为p个复合型,A1…AK,k=1,2…p。复合型按照如下标准划分,按照排序第一个复合型包含p(k-1)+1,k=1,2…m位置处的样本点,第二个复合型包含p(k-1)+2,k=1,2,…,m位置处的样本点。以此类推。
(5)复合型进化。按复合型进化算法(CCE)分别进化各个复合型,在后面将详细叙述。
(6)复合型混合。把进化后的每个复合型的所有顶点组合成新的点集,再次按目标函数值f升序排列。
(7)收敛性判断。如果满足收敛条件或者累计进化代数达到总进化代数,终止循环;否则返回步骤(4)。若累计进化代数达到总进化代数,但未得到优化结果,终止循环后调整参数重新进行计算。
SCE-UA方法一个关键的组成部分是步骤(5)中提到的复合型竞争进化法则。其基本步骤如下:
(1)初始化,选取参数q,a,b,其中2≤q≤m,a≥1,b≥1。

(3)根据权重在复合型Ak中选择q个父个体(因此q即是每个子复合型中样本点的个数),u1-uq记作集合B,并将父个体在Ak中的位置记作集合L。
(4)通过如下几步产生子个体:
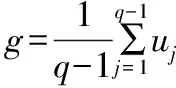
②计算新个体r=2g-uq(反射)。
③如果r在可行解区域内,则计算该点的目标函数值fr并继续进入第④步。否则在可行域范围内随机产生新个体z,使r=z(突变)。
④如果fr ⑤如果fc ⑥重复①~⑤步a次。 (1)地下水流动方程。根据Darcy定律以及质量守恒,不考虑水的密度变化条件下,三维空间孔隙介质中地下水流动的偏微分方程[18]: 式中:Kx、Ky、Kz分别为渗透系数在x、y、z方向上的分量;W为源汇项,用以表示流进汇或来自源的水量;h为含水层水位标高;Ss为含水介质的贮水率;t为时间。 (2)污染物迁移的数学表达式[19]: 在本次优化模型的设计中,地下水流数值模型MODFLOW和溶质运移数值模型MT3DMS用来模拟污染物在地下水中运移的时空分布特征。由于MODFLOW和MT3DMS具有模块化设计的特点,因此能够将其非常方便的耦合到优化模型中,并且能够针对不同的模块进行单独处理。 1.3.1 数值模型与优化模型的耦合 如何实现地下水数值模型(MODFLOW、MT3DMS)和优化模型的有效耦合是决定地下水污染强度优化识别能否高效执行的关键因素。传统的优化模型往往是将MODFLOW和MT3DMS作为单独的外部可执行文件进行调用,并且数据传递是通过文件读写进行。由于符合精度要求的反演结果往往需要成百上千次调用数值模型,通过调用外部可执行文件的方式会造成优化模型的反演效率非常低下。特别是当数值模型模拟范围大、网格剖分精细和反演问题复杂时,反演识别的时间通常需要几天甚至十几天,这种优化识别时间是无法忍受的。为了解决这个问题,本次研究将SCE-UA程序改写为主程序,将MODFLOW和MT3DMS分别作为两个子程序,在此基础上编写了进行子程序调用的接口程序。优化过程中,当主程序需要获得地下水流和污染物的有关运移特征时,则通过接口程序对两个子程序进行调用(如图1所示),以此模拟求解污染物运移的时空分布状况,并将模拟结果通过变量返回到主程序中。由于实现了数值模型和优化模型的内部耦合及数据交换传递由文件读写改进为内部变量传递,可以显著提高优化模型的执行效率。 图1 数值模型与优化模型的耦合 1.3.2 目标函数 反演识别过程中的决策变量是地下水污染强度q,而状态变量则是质量浓度C。目标函数E定义为: (3) 图2 优化模型求解流程 1.3.3 非稳定流反演问题 本次优化模型对非稳定流数值模型的反演采用如下策略,即先反演识别第一个应力期污染源强度信息,然后对所有的反演结果进行排序,用第一个应力期污染源排放浓度的最优反演结果来反演第二个应力期污染源排放浓度;然后在第二个应力期最优解的基础上反演第三个应力期,依次类推,直到所有的应力期反演识别结束。此种设计能够确保每一个应力期均使用优化模型反演的最优解,可以充分保证反演的精度。但是需要指出的是由于当前应力期的反演是基于上一应力期的反演结果,因此上一应力期的反演误差也会累积到当前应力期,这样造成反演误差会随着应力期的增多不断被放大。为了减少误差的累积,对于非稳定流问题的反演需要通过相应增多反演代数或者种群个数来提高每一应力期的反演精度。 如图3所示,研究区为一二维均质各向同性的矩形承压含水层(100 m×100 m),用边长为10 m的正方形网格将整个研究区域剖分为10行10列的有限差分网格(案例模型参考Singh等的污染物反演模型)[20]。含水层厚度为10 m,上下边界为隔水边界,左右边界为水头边界(左边界水头由上到下线性变化,上侧水头为9.7m,下侧水头为0.4m;右边界水头为7 m)。含水介质渗透系数为1 m/d,孔隙度为0.3,弥散度为20 m;反演时污染物排放浓度变化范围设定介于0~100 mg/L之间。由于本次案例研究的主要目的是评价优化模型的反演效果,因此在进行地下水数值建模时对研究区水文地质条件进行了一定程度的概化。 表1 不同进化代数时反演结果 通过表1可以看出,所开发的优化模型可以迅速反演识别出污染物排放浓度:在进化代数为10代时,反演误差(|反演值-真实值|/真实×100)为3.13,基本可以满足精度的需要;随着进化代数的增加,反演误差值逐渐变小,说明反演精度提高;在进化代数为50代时,可以精确的反演出排放浓度。但需要指出的是,随着进化代数的增加会带来很大的计算负担,造成反演时间增加,因此反演过程中要很好的在反演精度和反演效率之间做出平衡。 在进化代数为300代时,反演浓度随代数增加的变化趋势如图4所示。通过图4可以看出优化模型浓度反演最优值基本在15代后已达到稳定;浓度反演平均值一开始偏离真实值,但在50代左右基本稳定;浓度反演最差值一开始也偏离真实值,但在100代左右也可以达到稳定状态。说明优化模型已经求解到最优解,并且与其他相似优化模型相比,该SCE-UA优化模型求解的收敛速度也较快。 图4 反演浓度随代数增加的变化趋势 图5 案例2含水层示意图(单位:m) (2)案例2。为一非稳定流模型(共有12个应力期),有两口井污染井1和污染井2分别位于模型(3, 2)和(5, 5)处,并在12个应力期分别以30和80 mg/L的定浓度向地下水中排放污染物;在其下游(3, 8),(4, 6),(6, 9)和(7, 8)处有四口监测井,以四口监测井的污染物监测浓度,利用优化模型反演识别污染源处12个应力期的污染物排放强度。 反演识别结果如图6、图7所示。从图6可以看出,当进化代数为20代时,两口污染井的反演结果都出现比较剧烈的震荡[特别是(3, 2)处井],这主要是因为对于非稳定流的模拟,下一应力期的模拟需要用到上一应力期的反演结果,因此会造成反演误差的累积,使得模拟结果变差;随着进化代数增加到50代,虽然反演结果在某些应力期仍然有轻微的震荡,但已基本能满足反演精度的需要;当进化代数增大到100代,浓度反演值与真实值已非常接近,能够取得满意的反演结果。由此也可以看出随着非稳定流应力期的增加,需要相应增加进化代数以获得更加准确的反演结果。 图6 不同进化代数条件下污染井1(3, 2)处反演识别结果 图7 不同进化代数条件下污染井2(5, 5)处反演识别结果 图8 案例3含水层示意图(单位:m) (3)案例3。案例3更接近实际情况,两口污染井污染物的排放浓度不是定浓度排放,而是随着时间的变化而变化,其中旱季排放的少,雨季排放的多(如图9所示);同时与案例2相比,在(4, 6)和(9, 9)处分别增加了两口监测井;通过六口监测井的污染浓度监测值,反演两口污染井在不同应力期污染物排放强度的变化。 图9 进化100代时(3, 2)和(5, 5)处污染井真实值与反演值 通过图9可以看出,进化代数为100代时,优化模型可以非常好的反演识别不同应力期污染源的排放强度,反演值与真实值都较为接近,能够满足反演精度的要求。说明通过增加进化代数可以有效减少反演误差在不同应力期之间的累积;优化模型对于多污染源不定浓度排放时污染源强度的反演同样可以取得令人满意的结果。 通过以上3个不同污染物排放情景实例的反演,进一步说明在足够进化代数前提下,所提出的基于SCE-UA算法的地下水污染强度反演优化模型均能够获得令人满意的结果。 通过污染物浓度监测数据推求污染源排放强度是典型的求逆问题。本次研究将优化算法和地下水数值模拟程序结合起来,建立了一种优化搜索模型,并进行了不同案例情况下的反演验证。 (1)研究将优化算法SCE-UA和地下水数值模拟程序MODFLOW和MT3DMS结合起来,大大丰富了搜索行为,提高了反演识别的能力和效率。 (2)通过案例1的测试,在进化代数较少的情况下优化模型即可高效、准确的搜索污染源污染物排放强度;且反演结果的准确度随着进化代数的增大而增加。但需要注意的是,进化代数的增加同样会带来很大的计算负担,反演时间亦会相应增加。 (3)对于非稳定流的测试,由于不同应力期之间反演误差的累积,反演精度会随着应力期的增多而减小,需要相应增加进化代数以获得更加准确的反演结果。 (4)在足够进化代数的前提下,优化模型可以非常好的反演识别不同应力期多污染源排放强度的变化。 □1.2 地下水控制方程
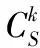
1.3 反演优化模型

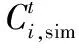

2 算例研究
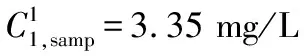



3 结 论

