全钢双芯板屈曲约束支撑的有限元分析

石文龙 张润键

（1.上海大学土木工程系，上海200444；2.上海史狄尔建筑减震科技有限公司，上海200092）

0 引 言

随着建筑行业的快速发展，减震装置越来越广泛地被应用于建筑结构的设计中。传统的支撑虽然在一定程度上提高了结构整体的刚度，但其在大震作用下容易发生屈曲。而屈曲约束支撑能够很好地解决大震作用下支撑屈曲的问题。屈曲约束支撑在小震及风荷载的作用下处于弹性状态，能为主体结构提供侧向刚度；在中震、大震及强震作用下，屈曲约束支撑能提前进入耗能状态。通过耗散大部分地震能量来保护主体结构。屈曲约束支撑又称为防屈曲支撑、无粘结支撑，主要由芯板和外围约束构件组成。传统的屈曲约束支撑外围约束构件由钢套筒中填充混凝土构成。近些年来，为了减少屈曲约束支撑加工过程中湿作业的工作量，降低支撑自身的重量，新型的纯钢型屈曲约束支撑逐渐成为研究重点。

为了克服单核心屈曲约束支撑与主体结构连接段长度较长、螺栓数量多的缺点，蔡克栓等［1］研制出双钢管型挫屈束制消能支撑，并进行了缩尺试验；胡宝琳、石文龙等［2］提出一种新型的双芯板防屈曲支撑，并对其进行了有限元模拟，通过对芯板宽厚比、芯板与外套筒间隙以及摩擦系数等影响因素进行模拟分析，给出了相应的参数选取建议；王玉梅、王爽［3］设计了一种可拆解组合的全钢双芯核防屈曲支撑并对其进行试验分析及数值模拟分析，研究结果表明，该支撑的耗能能力、残余刚度和强度能满足其作为抗震耗能构件的需要，但约束单元需保证具有足够的握裹强度，试件端部连接可靠，才能保证核心单元性能的发挥；为研发轻质高性能的防屈曲支撑，黄镇等［4］提出了一种新型横肋约束防屈曲支撑并对其进行了试验研究，设计了3 组BRB 试件并进行了低周往复加载试验，研究结果表明，横向加劲肋可以为核心单元提供足够的侧向刚度，有效抑制核心单元的屈曲；丁婷等［5］提出了一种新型外围机制，外围约束单元采用钢套管结合横向加劲肋和钢套管结合纵向加劲肋两种形式。通过数值模拟的结果得出结论：支撑横向加劲约束下的核心构件在轴压作用下有发生局部屈曲失稳的趋势，在相同的轴向加载下，其受力性能劣于纵向加劲约束下的支撑构件，而横向加劲肋的疏密程度也会影响核心构件侧向变形分布及失稳模式；林当凯和蔡崇兴［6］对多节强化式防屈曲耗能支撑进行疲劳测试试验，试验结果表明，采用钢板或钢管作为支撑的约束单元都能提供良好的约束作用。采用多段设计可提高核心单元的屈曲轴力，且因核心单元的消能段变短，支撑在较小的应变下便能进入屈服状态；刘怡、蔡崇兴［7］对多节强化屈曲约束支撑进行缩尺度模型测试，根据缩尺原理设计了两组不同屈服力的试件，测试结果表明，两组试件均具有良好的耗能能力，且试验结束后，拆开试件发现破坏位置位于消能段，符合设计的要求。

本文提出了一种新型全钢双芯板屈曲约束支撑，设计了27 个支撑试件，按《高层民用建筑钢结构技术规程》［8］附录 E.4.1 的规定，采用 ABAQUS软件对各试件进行轴向往复拉压受力性能的模拟，研究了内核单元与约束单元间隙、约束单元钢板厚度、加劲肋排布方式对支撑性能的影响。

新型双芯板屈曲约束支撑主要由外套筒和两块芯板构成，外套筒由五块钢板焊接而成，其上焊有加劲肋来增加外套筒的刚度，同时，其内部焊接有限位块。芯板采用两段式设计，在中间设有限位卡，通过外套筒上的限位块对芯板在长度方向上进行变形限制。由于核心板消能段较短，支撑易到达屈服应变，能够较早提供消能的能力。同时，限位卡还可以防止外套筒与芯板的相对滑动。芯板两端设置加劲肋，增加连接段的面外刚度，芯板过渡段采用斜截面，防止应力突变从而导致芯板在过渡段发生失稳。芯板表面涂刷无粘结材料，以减小在轴压状态下芯板发生多阶屈曲变形时与外套筒的摩擦力。支撑总长度为3 m，约束单元长度为2.8 m，其中核心单元采用Q235 钢材，约束单元采用Q345 钢材，图1 为试件DB-2 各部件的具体尺寸，图2为试件DB-2的组装构成。

对比混凝土约束的屈曲约束支撑，该支撑具备以下几个特点：①通过采用加劲肋的方式，可在支撑具有良好滞回性能的前提下减少约束套筒的重量、节约材料成本；②相比单核心屈曲约束支撑，采用双核心形式的屈曲约束支撑在施工现场更容易连接到节点板上；③支撑整体全部采用钢材制作而成，取材容易，制作周期短。

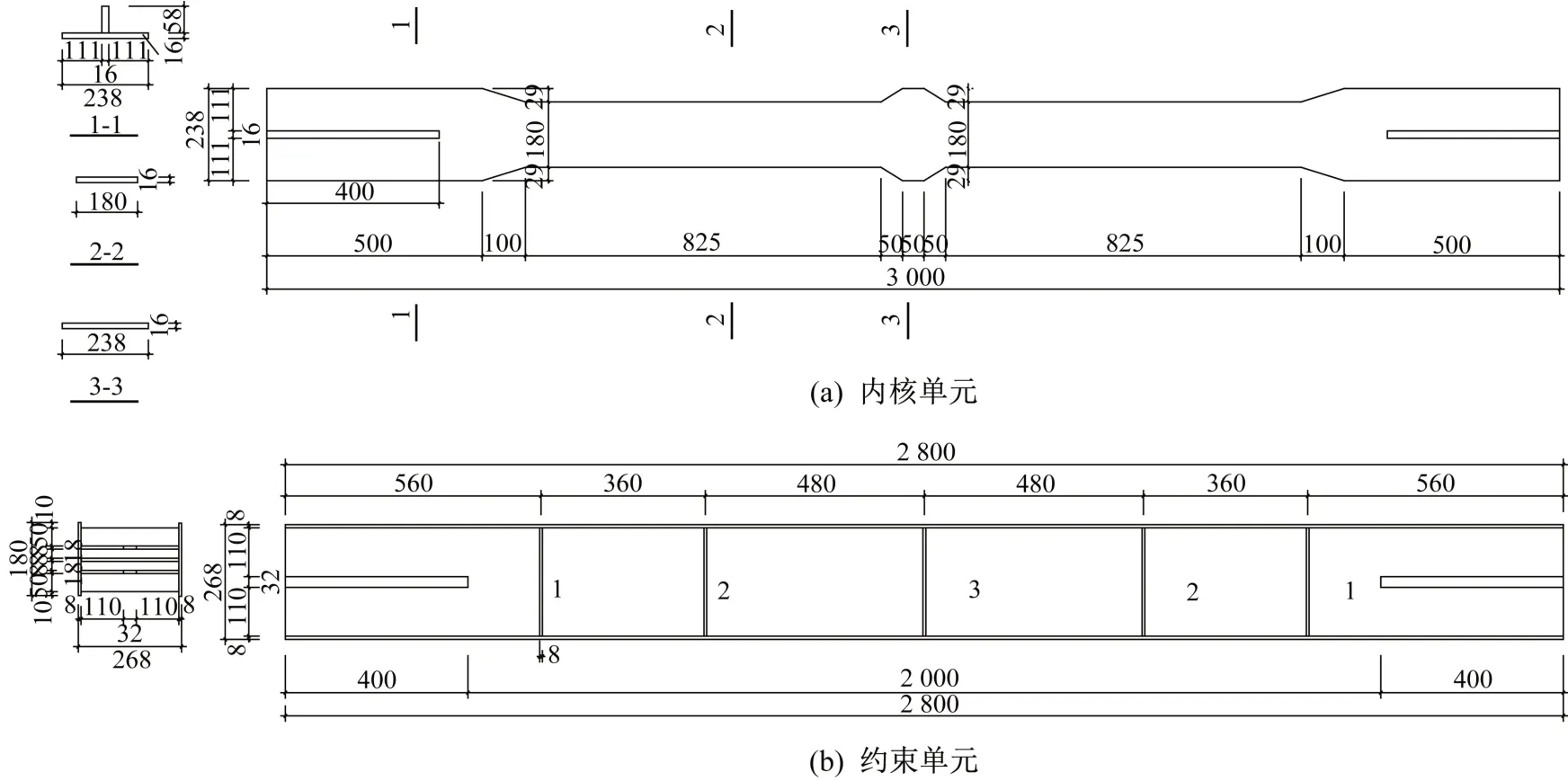
图1 试件DB-2尺寸与构造（单位：mm）Fig.1 Size and constructional detail of DB-2（Unit：mm）

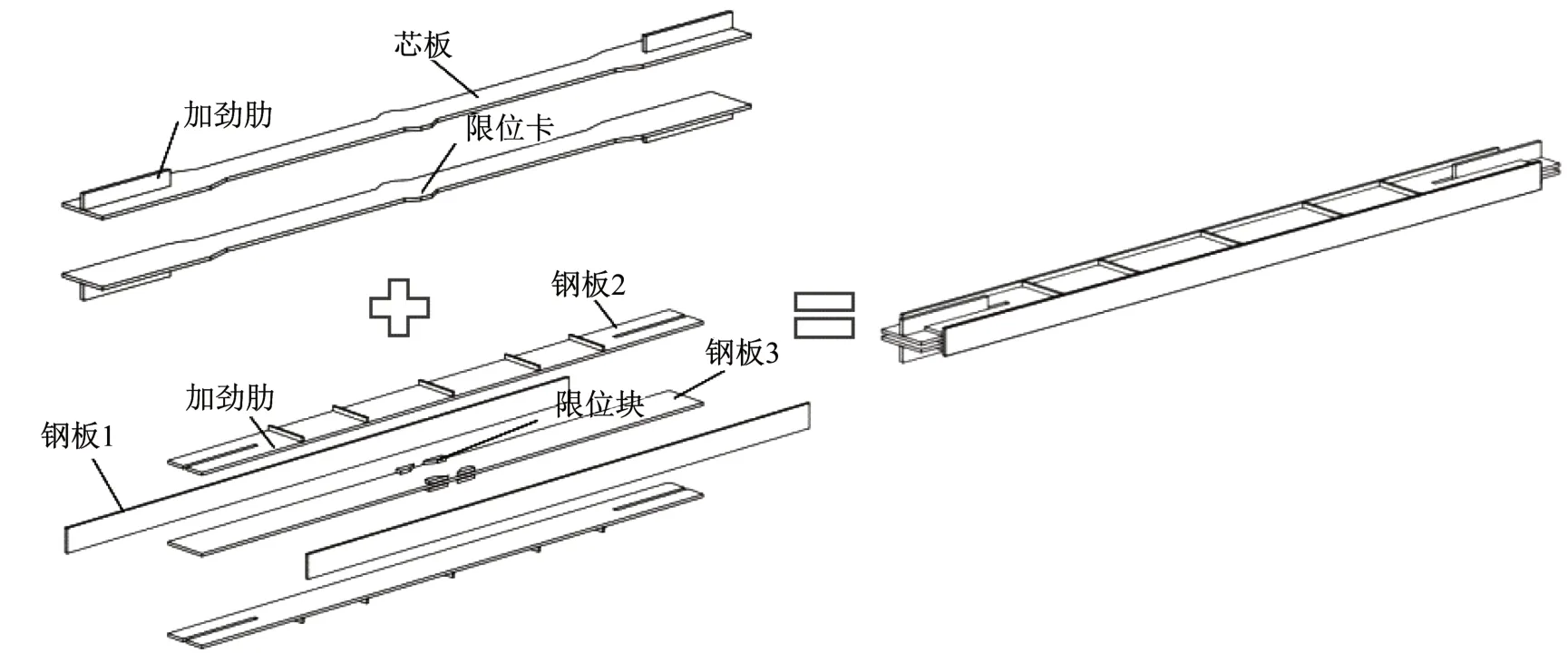
图2 试件DB-2组装图Fig.2 Assembly diagram of DB-2

1 有限元模型的建立

1.1 材料本构与单元的定义

全钢双芯板屈曲约束支撑钢材选用Q235 与Q345 两种材料，芯板采用Q235 钢材，其余组件均采用Q345 钢材。钢材的本构模型见图3，弹性模量E取值为206 GPa，切线模量为0.02E，泊松比为0.3。钢材的应力-应变关系采用理想双线性随动强化模型。为了更好地模拟全钢双芯板屈曲约束支撑在轴向拉压下各部件的变形状态，支撑的内核单元与约束单元均采用C3D8R 来定义（8 节点六面体减缩积分实体单元，沙漏控制）。

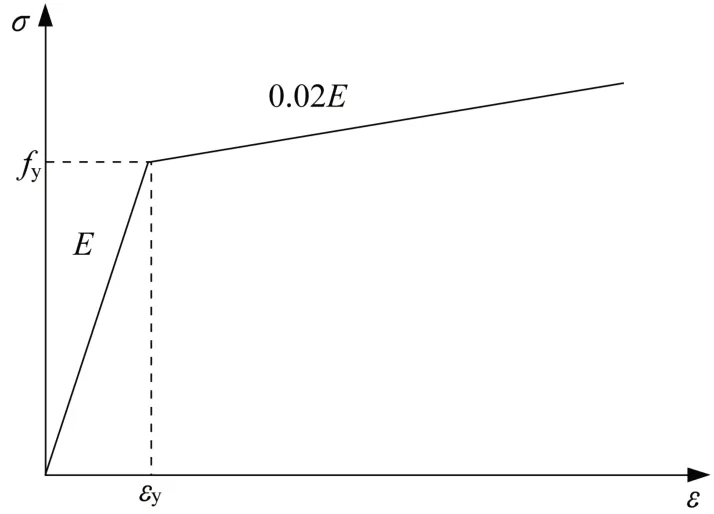
图3 钢材的本构模型Fig.3 Constitutive model of steel

1.2 接触关系

全钢双芯板屈曲约束支撑有限元模型的接触关系有两种——tie 接触与相互接触。相互接触属性分为法向行为与切向行为。法向行为设置硬接触，切向行为设置为无摩擦。核心单元与约束单元之间采用相互接触，其余部件连接采用tie接触。

1.3 加载制度与边界条件

根据《高层民用建筑钢结构技术规程》［8］附录E.4.1 规定，耗能型屈曲约束支撑的单轴试验应按下列加载幅值及顺序进行：依次在1/300（10 mm）、1/200（15 mm）、1/150（20 mm）、1/100（30 mm）支撑长度的位移水平下进行拉压往复加载，每级位移水平下循环加载3 次（图4）。支撑的端部边界条件为一端固定，另一端铰接。采用轴向位移加载。有限元模型见图5。

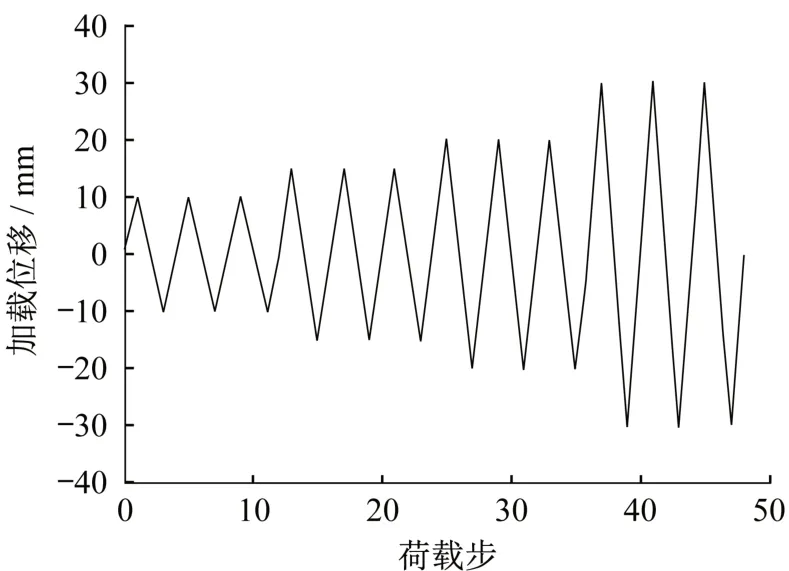
图4 加载幅值曲线Fig.4 Loading amplitude curve

图5 有限元模型Fig.5 Finite element model

2 有限元模型的验证

本文通过对史庆轩等［9］研制的全钢装配式屈曲约束支撑进行模拟（图6，选取文献中试验件QBRB4），验证有限元模型的合理性。模拟结果与试验结果的滞回曲线对比如图7 所示，结果参数对比如表1 所示。可知，除塑性刚度误差较大外（达到20.0%），其余参数误差较小。而塑性刚度相差较大是因为有限元分析中芯板与外套筒的摩擦系数设置为0，试验过程中摩擦力的存在会影响塑性刚度的大小。有限元分析得到的滞回曲线与试验滞回曲线吻合较好，说明有限元模型的建模方式是可行的。

图6 全钢装配式屈曲约束支撑有限元模型Fig.6 Finite element model of all-steel assembled buckling-restrained brace

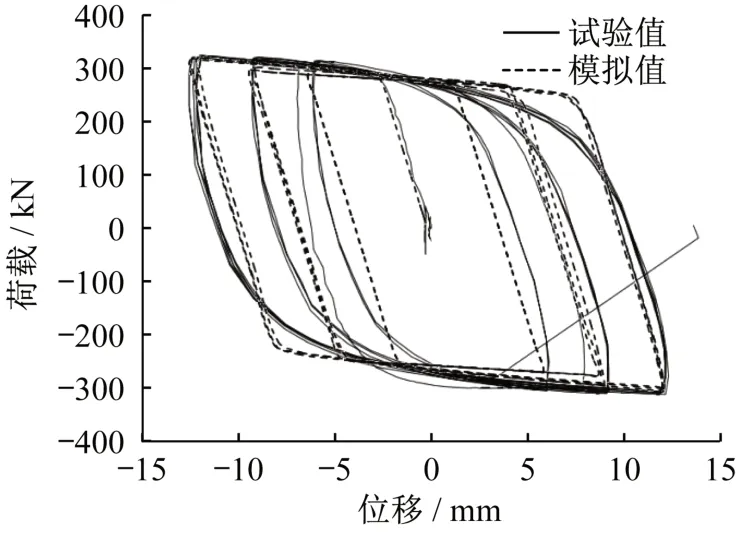
图7 滞回曲线对比Fig.7 Contrast of hysteresis curves

3 支撑性能的影响因素分析

3.1 内核单元与约束单元的间隙

内核单元与约束单元预留的间隙是为了使内核单元的约束屈服段在高阶模态下发生高阶微幅屈曲及容许芯板在受压状态下膨胀。试件DB-1—DB-7的内核单元与约束单元间隙大小从0.5 mm、1 mm、1.5 mm、2 mm、2.5 mm、3 mm、4 mm 进行变化，通过对各个支撑进行1/100 支撑长度单轴压缩模拟，研究内核单元与约束单元间隙对支撑性能的影响，得出曲线如图8 所示：当间隙取值为0.5 mm 与1 mm 时，曲线未出现明显波动，随着加载位移的加大，支撑的承载力平稳上升；当间隙取值大于或等于1.5 mm 时，曲线波动明显，且随着间隙的增加，波动幅度越大，承载力下降越大。原因是过大的间隙使支撑在轴压状态下，约束单元无法为芯板提供足够的约束力，芯板发生幅值过大的变形，导致支撑承载力下降，影响支撑的耗能性能。为了便于支撑性能的发挥，支撑的间隙应取0.5～1 mm。

表1 试验结果与有限元分析结果参数对比Table 1 Comparison between experimental results and finite element analysis results

图8 不同间隙下的支撑承载力曲线Fig.8 Bearing capacity curves of supports with different clearances

3.2 加劲肋的布置

试件DB-8-DB-10 取消加劲肋布置，约束单元板厚分别取值为8 mm、10 mm及12 mm。为满足外围约束单元具有足够的刚度，避免支撑受压时整体屈曲。试件的约束比通过式（3）计算，得出各试件约束比为 1.79、2.33 与 2.92，均满足 Watanabe［10］建议实际使用时约束比不小于1.5的要求。

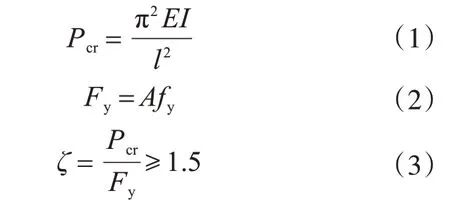
式中：E为约束单元钢材弹性模量；I为约束单元弱轴惯性矩；l为支撑长度；A为芯板约束段面积；fy为芯板钢材屈服强度。

通过分析得到不同厚度下支撑滞回曲线如图9所示。从图9可以看出，在不布置加劲肋的情况下，当厚度取值为12 mm（DB-10）时，支撑的滞回曲线比较饱满，而随着厚度的减小，约束单元的刚度下降，芯板在受压状态下屈曲变形滞回曲线的饱满度下降。当厚度取值为8 mm（DB-8）时，滞回曲线出现了内缩，承载力下降。且从表2 可知，板厚较小时，试件DB-8 与DB-9 各部件的应力与变形值均相对较高，芯板应力达到390 MPa 以上，支撑可能发生破坏。而试件DB-2 约束单元厚度为8 mm，约束单元上布置五排加劲肋，得到滞回曲线如图10所示。从图10中可以看出，该支撑在各幅值加载下滞回曲线比较饱满，对比试件DB-8，加劲肋的使用可使该支撑约束单元钢板厚度在同为8 mm 的情况下仍具有良好的滞回性能。与试件DB-10各部件应力与变形值水平相差较小的情况下，加劲肋的布置可使试件DB-2约束单元的用钢量节约30%以上。表明加劲肋的布置可有效地提高约束单元的刚度，保证支撑在变幅值单轴拉压作用下的稳定性与耗能性能。

图9 DB-8-DB-10滞回曲线Fig.9 Hysteresis curves of DB-8～DB-10

3.3 加劲肋布置方式

试件DB-13-DB-28 外围约束单元布置了四排加劲肋，本节通过增加最外排加劲肋与中间排加劲肋的间距La，缩小中间两排加劲肋的间距Lb，研究加劲肋的布置方式对支撑各部件的应力变形及耗能指标的影响。

3.3.1 各部件最大应力及最大变形对比

从表2 各部件的最大应力值可以得出，在La从160～760 mm变化的区间内，各部件应力数值总体呈现先下降后上升趋势。芯板应力区间为361～419 MPa。部分试件的内核单元出现应力过大的情况，原因是由于加劲肋间距过大，约束单元无加劲肋约束的区段无法为芯板提供足够的约束力，约束单元见图11。在支撑受压状态下发生鼓曲，导致芯板在该处发生较大的变形，产生应力集中，无法实现芯板的全截面屈服。如图12 所示为试件DB-25 的应力云图，从图中可知该试件的最大应力达到418.6 MPa，应力集中区域有可能超过材料的极限强度而发生破坏。而合理的排布间距可以实现内核单元的全截面屈服，如图13 所示为试件DB-20 的应力云图，相比试件DB-25，试件DB-20 加劲肋的布置间距La较为适中，芯板可实现全截面屈服；而约束单元钢板2 应力区间为 204～308 MPa，钢板3 的应力区间为192～310 MPa，表明各试件约束单元在加劲肋不同排布的情况下均未达到其屈服强度。而加劲肋的应力区间则在302～347 MPa 的范围内，表明在加劲肋间距变化情况下，部分试件的加劲肋进入屈服状态。从表2 各部件的最大变形值可以得出，钢板2和钢板3变形值在La从160～760 mm变化的区间内，同其应力值一样总体呈现先下降后上升的趋势，而加劲肋变形值相对比较平稳。约束单元钢板2 变形值区间为6.6～12.9 mm，钢板3 的变形值区间为5.0～10.8 mm，加劲肋的变形值区间为0.51～1.62 mm。约束构件各部件的变形值均在合理范围内。

表2 各试件约束单元尺寸Table 2 The constraint unit sizes of each specimen mm

3.3.2 各试件滞回曲线对比

加劲肋不同的布置间距会影响支撑滞回曲线的饱满程度，图14-图18为试件DB-8-DB-27的滞回曲线。其中DB-16、DB-17、DB-18和DB-19的滞回曲线比较饱满，此时La取值适中。而其余试件的滞回曲线均出现不同程度的内缩，即发生在加劲肋间距较大的情况（表现为La取值过大或者过小时）。

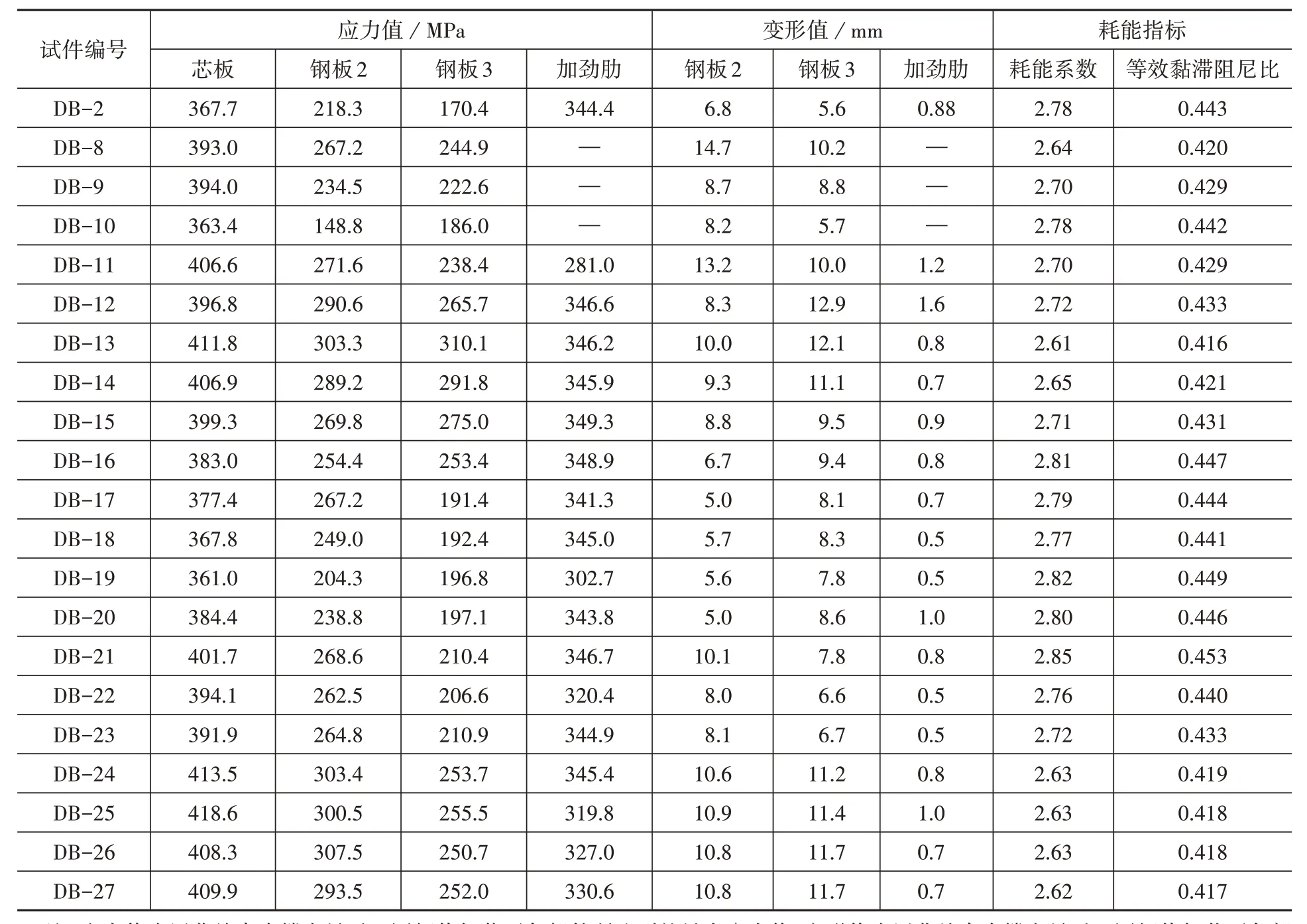
表3 各试件结果参数对比Table 3 Comparison of parameters of each specimen

图10 DB-2与DB-8滞回曲线Fig.10 Hysteresis curves of DB-2 and DB-8

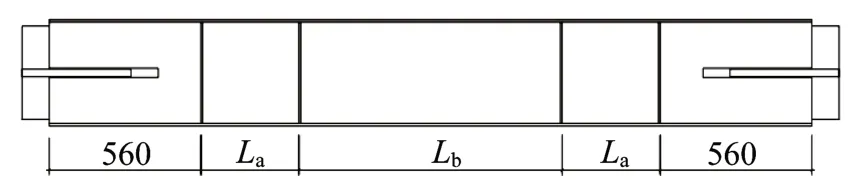
图11 约束单元（单位：mm）Fig.11 Constraint unit（Unit：mm）

图12 DB-25内核单元应力云图Fig.12 Stress contour of DB-25 core element

图13 DB-20内核单元应力云图Fig.13 Stress contour of DB-20 core element

图14 DB-8-DB-11滞回曲线Fig.14 Hysteresis curves of DB-8-DB-11

图15 DB-12-DB-15滞回曲线Fig.15 Hysteresis curves of DB-12-DB-15

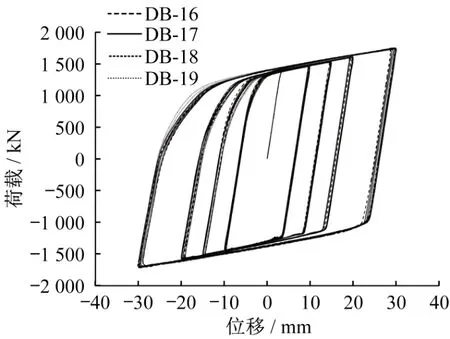
图16 DB-16-DB-19滞回曲线Fig.16 Hysteresis curves of DB-16-DB-19

图17 DB-20-DB-23滞回曲线Fig.17 Hysteresis curves of DB-20-DB-23

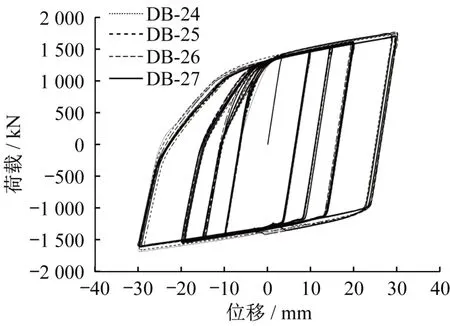
图18 DB-24-DB-27滞回曲线Fig.18 Hysteresis curves of DB-24-DB-27

3.3.3 各试件等效黏滞阻尼比及耗能系数对比

耗能系数和等效黏滞阻尼比是反映非线性结构耗能能力的两个重要指标，支撑的耗能情况可由耗能系数与等效黏滞阻尼比［11］来表征。分别按式（4）、式（5）计算：

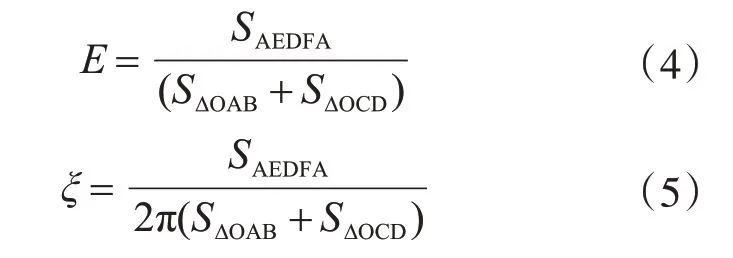
式中：SAEDFA为一个滞回环的面积；S△OAB与S△OCD为△OAB与△OCD的面积。

从表3 可知，各支撑试件的耗能系数与等效黏滞阻尼比分别在2.6 与0.41 以上。其中的加劲肋间距较为均匀的试件耗能数值较高，表现出良好的耗能性。

3.3.4 结果分析

综上，当La的大小控制在 360～480 mm 时，支撑能表现出良好的耗能性能。原因是由于芯板采用分段设置，中间刚性段的存在使得芯板的耗能段由中间向刚性段的两端转移，如图19 所示。而加劲肋为设置在集中荷载处，保证构件局部稳定并传递集中力所设置的加强件。故加劲肋设置在芯板变形较大的区域（耗能段）的试件具有较好的局部稳定性，表现出良好的耗能性能。

图19 耗能段转移示意图Fig.19 Transfer of energy consumption section

对比试件DB-2，试件DB-11 取消了图1 中外套筒两排2 号加劲肋，试件DB-17 取消了外套筒中间一排3 号加劲肋。试件DB-11 由于在芯板耗能段无布置加劲肋，外套筒无法提供足够的约束力，造成芯板局部产生应力集中，应力值较大，可能发生破坏。而试件DB-2 中由于3 号加劲肋布置在中间刚性段处，芯板在该区域本身变形较小，所以试件DB-2 与试件DB-11 在各部件应力值、变形值与支撑整体耗能指标的结果相近，进一步验证了上述结论。

4 结 语

（1）本文通过数值模拟的方法，研究全钢双芯板屈曲约束支撑的耗能性能，结果表明：在轴向反复拉压试验中该支撑具有饱满的滞回曲线，耗能能力强。

（2）过大的支撑间隙会导致支撑承载力曲线波动幅度较大且承载力下降，为保证支撑性能的发挥，支撑的间隙应取0.5～1 mm。

（3）不布置加劲肋的支撑试件随着约束单元钢板厚度加大，支撑滞回曲线的饱满度上升，而布置加劲肋可满足在约束单元钢板厚度较薄的情况下仍能获得饱满的滞回曲线，约束单元用钢量可节省30%以上。

（4）加劲肋的排布间距会影响支撑的滞回性能，过大的间距会导致芯板产生应力集中从而发生破坏；而加劲肋设置在芯板的耗能段可有效限制芯板的局部变形，在加载过程中实现全截面屈服，支撑表现出良好的耗能性能。