混合隔震耗能结构基于Kanai-Tajimi谱的响应简明解析解
王善库 葛新广 李 钢 赵立菊
(1.信阳职业技术学院建筑工程学院,信阳46400;2.广西科技大学土木建筑学院,柳州545006)
0 引 言
隔震结构是一种抗震控制措施,最早由日本学者在 19 世纪 80 年代提出[1],经历一百多年的发展,是成功应用于实际工程中的少数结构减震控制措施之一[2-4]。隔震结构是利用抗侧刚度较小的隔震层将结构与基础或下部结构隔离开来,可有效降低地震能量向结构物的传递,从而提高了结构地震的安全性和舒适感,减少了非结构构件的破坏,具有造价低、施工方便的特点,在各种结构中都得到了广泛的应用[5-7]。根据隔震层设置位置的不同,因为又分为基底隔震[8-9]和层间隔震[10]两类。由于隔震结构具有显著的减震性能,一直受到广大科研人员和工程师的青睐。
然而,隔震层抗侧刚度小,其导致隔震层以上结构部分的刚性侧移较大,可能会与邻近建筑发生碰撞,为此,需要对隔震层设置限位装置。熊仲明等[11]利用摩擦垫既耗能又限位的特点,研究了其基于反应谱型地震激励下的隔震结构的地震动响应。展猛等[12]研究了以软钢圆锥棒为新型限位耗能装置在时程激励下的响应,并考虑了限位器非线性的特点。黏弹性阻尼器具有安拆方便、耗能效果好等优点,而被广泛采用[13-14]。隔震层+抗侧粘弹性阻尼器组成混合耗能减震结构,可为隔振层提供合适侧向变形空间同时充分利用黏弹性阻尼器变形大则耗能大的特点,可产生复合的减震效果,目前此类文献较少。
地震动是一种随机激励,已在工程界成为共识,自 1947 年 Housener[15]提出白噪声激励以来,各种随机激励模型被发明用来模拟地震动,如Kanai-Tajimi 谱[16-17]、Clough-Penzien 谱[18]、欧进萍谱[19]等,其中Kanai-Tajimi谱利用二阶微分方程作为滤波方程开创了利用微分方程表述随机地震动激励的先河,而 Clough-Penzien 谱[18]、欧进萍谱[19]等均是对Kanai-Tajimi 的改进,为此研究基于Kanai-Tajimi 谱地震动下的结构响应是研究基于其他地震动激励下的基础。周福霖等[20]利用状态方程法,研究了层间隔震结构基于Kanai-Tajimi地震的响应问题;邹万杰[21]利用传递函数法研究了带支撑的Maxwell 阻尼器多层隔振结构的基于Kanai-Tajimi地震动响应分析;李创第等[14]利用传递函数法研究了积分型黏弹性耗能减震结构基于Kanai-Tajimi地震动响应分析;以上这些分析仅获得结构的响应,且表达式比较复杂,且未给出谱矩分析。
基于Kanai-Tajimi谱下的地震动位移、速度及其谱矩分析的传统方法存在表达式复杂的窘况,本文提出了一种简明解析解法。首先利用达朗伯原理,获得单自由度混合隔震结构的地震动方程,并运用其基于白噪声的二阶微分方程来表述Kanai-Tajimi谱,将两者联立成运动方程组。利用复模态方法将混合隔震体系的响应化为基于白噪声激励下的响应。运用白噪声激励下响应的简明特点,获得混合隔震各种响应的简明解析解,基于Wiener-Khinchin 定律,得到结构响应的功率谱简明表达式,最后获得可靠度分析的0~2 阶谱矩的简明解析解。
1 混合耗能体系的运动方程
设置Maxwell 型黏弹性阻尼器侧向支撑的单自由度隔震混合耗能结构,其结构层质量、刚度、阻尼分别为m、k、c;隔震层的质量、刚度、阻尼分别为mb、cb、kb;布置如图 1 所示,根据达朗伯原理,在地震动作用下运动方程:
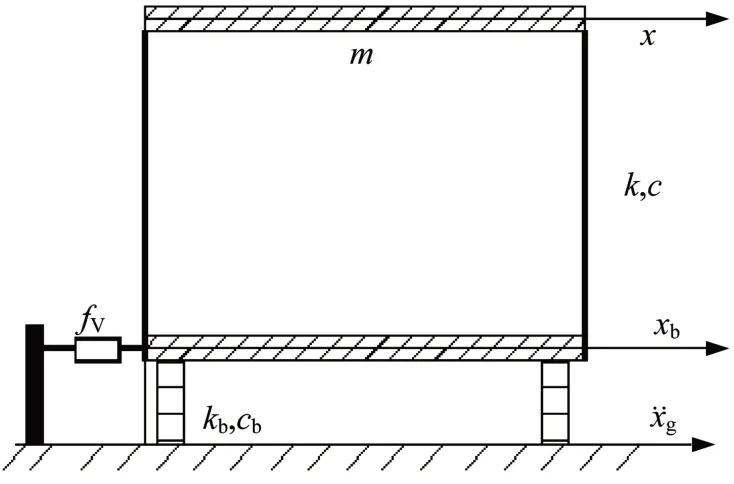
图1 计算简图Fig.1 Caculating diagram of dynamic system
隔震层:

结构层:
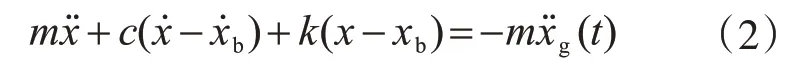
Maxwell黏弹性阻尼器[22]:


基岩运动为白噪声随机激励,具有均值为零,其协方差可表示:
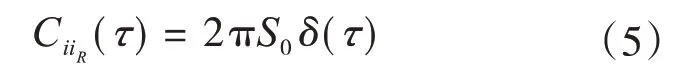
式中:S0为地震动强度常数;δ(τ)为Dirac函数。
地面的运动绝对加速度与地面相对于基岩、基岩绝对加速度存在如下关系:

引入状态变量:
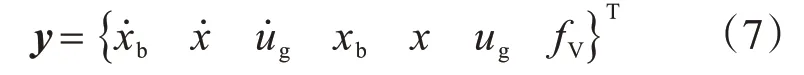
则式(1)-式(4)用矩阵形式表示为

式中:

式中,[·]T表示矩阵转置。
由式(8)可知,基于Kainai-Tajimi 激励的结构响应化为白噪声激励下的响应分析,可利用白噪声激励的简明特点获得结构响应的简明解。由于式(8)为一阶微分方程,属于状态方程形式,故采用复模态方法进行求解。
2 混合耗能体系响应的解析表达式
由复模态法理论[23]可知,式(8)存在左、右特性向量矩阵U、V和特征值矩阵P,满足关系式:

其中,特征值矩阵P为对角阵,其由式(8)的特征值方程决定:

左、右特性向量矩阵U、V的求解方法如下:
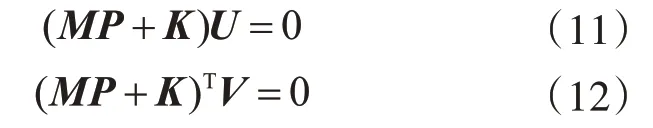
式中,U、V均为7阶矩阵。
为使方程式(8)解耦,引入复模态变量:

式中,Z为广义变量。
把式(13)带入式(8):

式(14)左乘左特征向量VT:
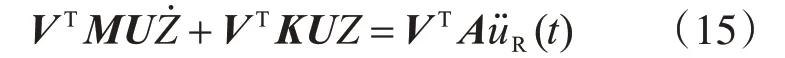
由复模态理论及式(8),式(15)改写为:

式中,γ为复模态阵型强度系数向量,其表达式:

式(16)的分量表达式:
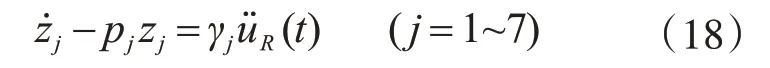
式中,zj、γj、pj分别为Z、γ、P的分量。
式(18)的杜哈梅形式解:
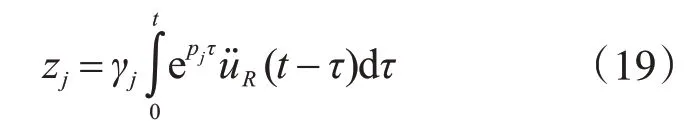
由式(7)及式(18),混合耗能体系结构响应的杜哈梅形式解:
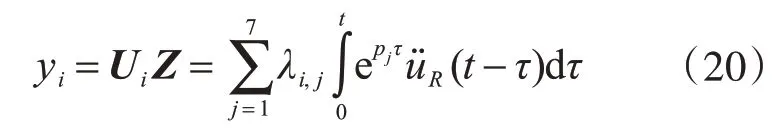
式中:yi表示式(7)中第i个响应分量;Ui为右特征向量矩阵的第i行向量;λi,j=Ui,j*γj,Ui,j为右特征向量矩阵的第i行、j列元素。
由随机振动理论,混合耗能体系某一响应的协方差:

把式(5)代入式(21):

利用Dirac 的函数性质,式(22)积分后改写为
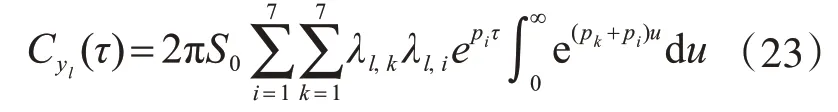
对式(23)运用积分:
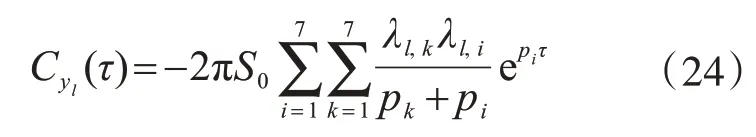
由式(24)可知,混合耗能体系基于Kanai-Tajimi 谱响应的协方差可用结构振动特征值函数的线性组合表示,简洁明了。
当τ=0 时,混合耗能结构某一响应的协方差即为结构响应的方差,由式(7)可知,
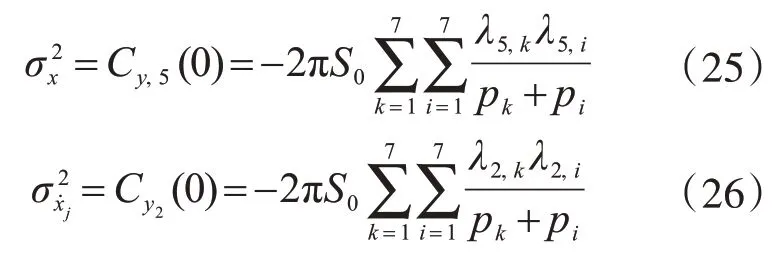
同理,隔振层的位移及速度的方差:
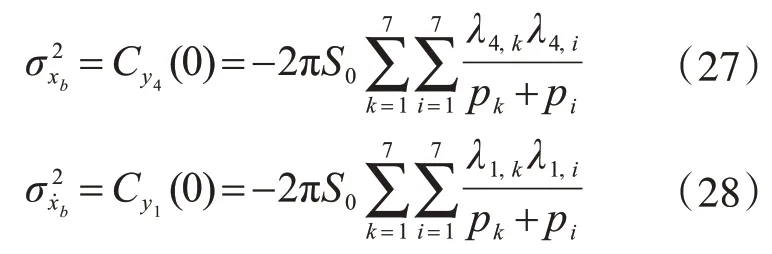
阻尼器阻尼力的方差:
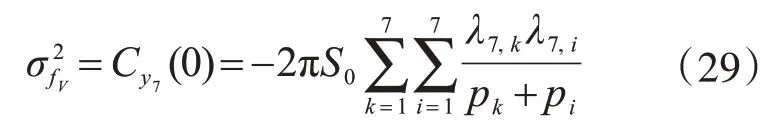
由式(25)-式(29),混合耗能减震结构基于Kanai-Tajimi 谱的响应方差可表示为结构各复模态强度振子与振动频率特征值的简单组合。
3 混合耗能体系响应的谱矩分析
由随机振动理论,可知单边功率谱与协方差存在Wiener-Khinchin关系[23]:
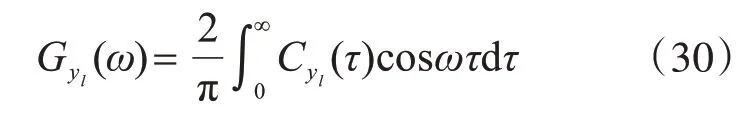
把式(24)代入式(30):

式(31)进行积分后整理为

由谱矩的定义,结构响应S的谱矩可表示为:

由文献,结构位移和隔震层位移的0阶和2阶谱矩与方差的关系:
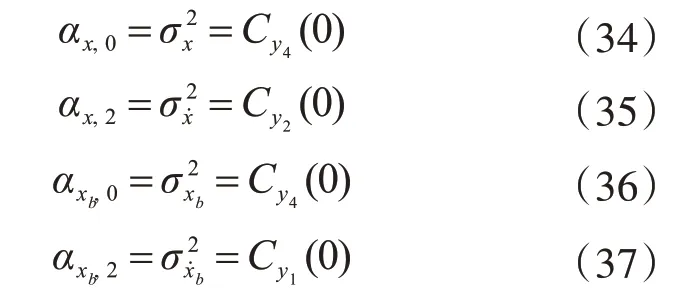
结构位移和隔震层1 阶谱矩的计算,把式(24)代入式(33)并令j=1:
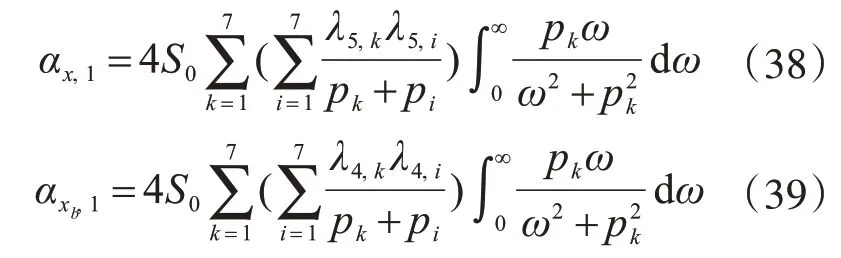
对式(38)、式(39)进行积分
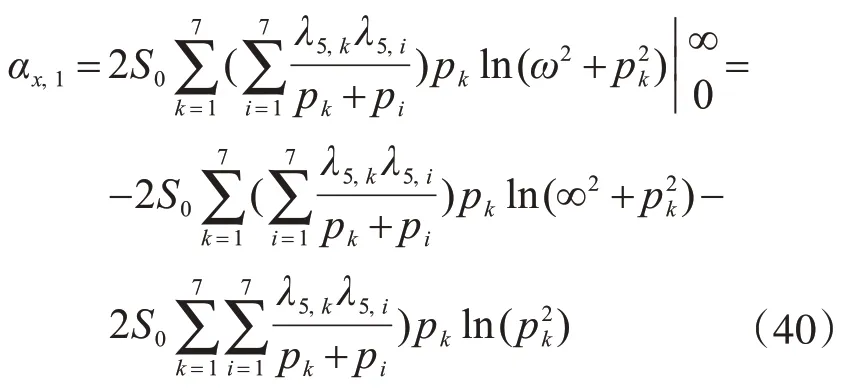
由于pk远小于∞,故式(40)变为

由于2 阶谱矩存在,则1 阶矩肯定存在,根据文献[23]可知,
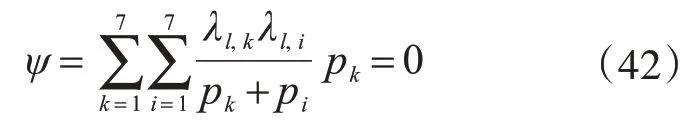
故结构位移和隔震层的位移1阶谱矩为
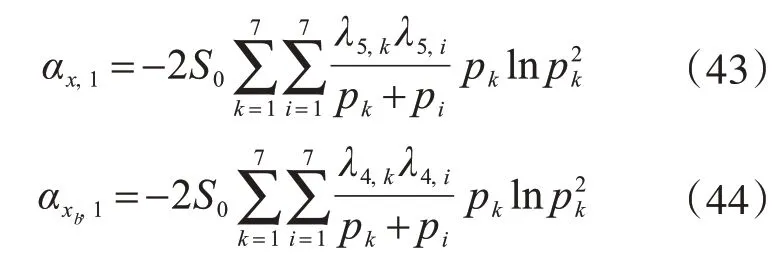
至此,式(34)、式(35)及式(43)为结构位移响应的0~2阶谱矩;式(36)、式(37)及式(44)为隔震层位移响应的0~2阶谱矩。
4 算 例
单层建筑结构,结构层质量400 t,结构层刚度为400×103kN/m,结构阻尼比为0.05。地震烈度为8 度,三类场,根据文献[19],谱强度因子S0=111.34 cm2/s-3。
Kanai-Tajimi 谱的场地参数:特征频率15.71 rad/s、场地阻尼比0.72。隔振层质量mb=450 t,kb=20×103kN/m,阻尼比 0.1。Maxwell 黏弹性阻尼器的参数为τ=0.1s;CV=15×103kN·s/m。
4.1 本文方法验证
Kanai-Tajimi作为地震动激励,其的功率谱不受结构参数的影响,而本文方法中,式(7)将地面运动ug作为耗能结构的未知参量进行求解,为此本文方法同样可以给出了地面运动的功率谱的新解,将其与Kanai-Tajimi谱的传统功率谱表达式进行对比,以验证本文方法的正确性。
由式(4)、式(6)可知:

由式(7)及(18),则式(45)改写为
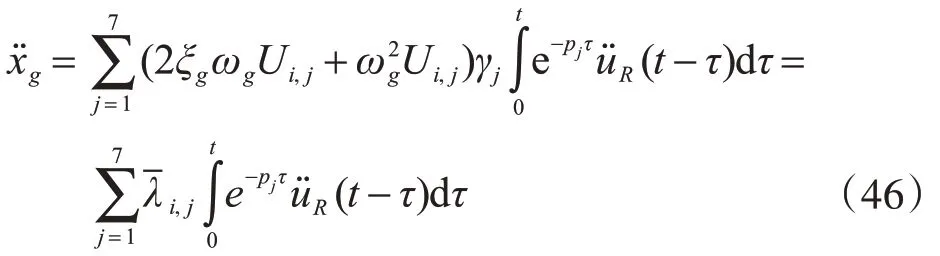
表 1 模态强度系数Table 1 Modal strength coefficient of
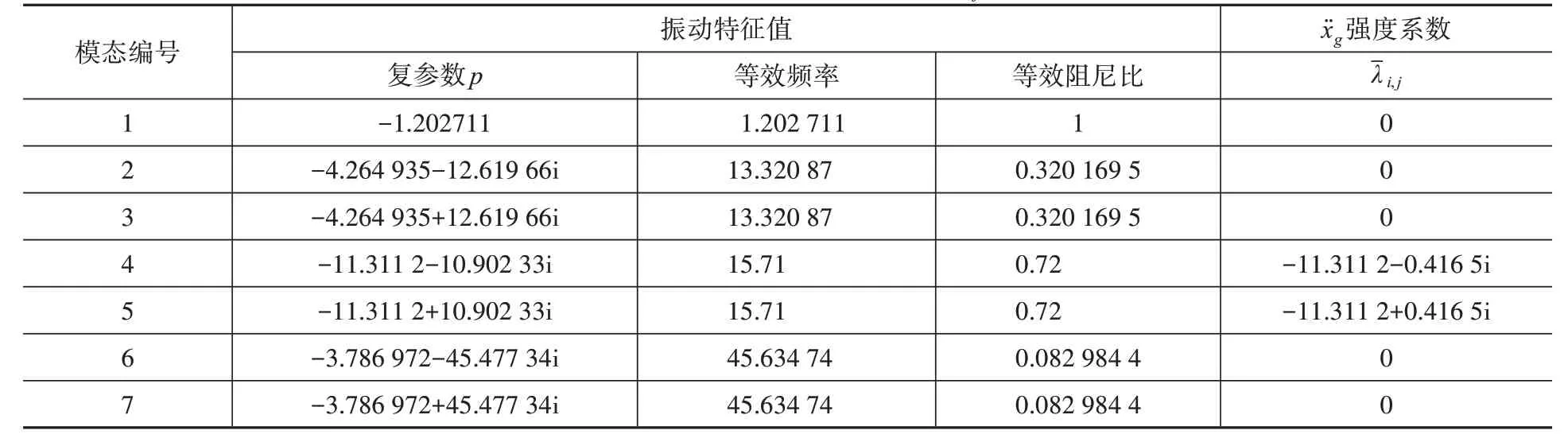
表 1 模态强度系数Table 1 Modal strength coefficient of
模态编号振动特征值x¨ g 强度系数-λ i,j 0 0 0-11.311 2-0.416 5i-11.311 2+0.416 5i 1 2 3 4 5 6 7复参数p-1.202711-4.264 935-12.619 66i-4.264 935+12.619 66i-11.311 2-10.902 33i-11.311 2+10.902 33i-3.786 972-45.477 34i-3.786 972+45.477 34i等效频率1.202 711 13.320 87 13.320 87 15.71 15.71 45.634 74 45.634 74等效阻尼比1 0.320 169 5 0.320 169 5 0.72 0.72 0.082 984 4 0.082 984 4 0 0
表1 中,等效频率为|p|、等效阻尼比为p的实部的绝对值与|p|的比值。模态4和模态5的等效频率和等效阻尼比均与Kanai-Tajimi 谱的场地振动参数相同,从式(4)的场地滤波方程可知,该方程是解耦的。同时强度系数仅模态4 和模态5为非零,说明结构的参数对场地加速度没有影响,从物理意义上说明本文方法的正确性。
由本文方法得到地面加速度的功率谱为
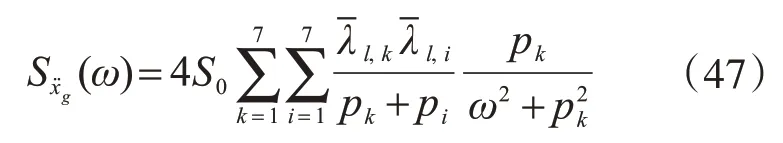

根据式(47)、式(48)分别绘两种方法的功率对比图,如图2所示。
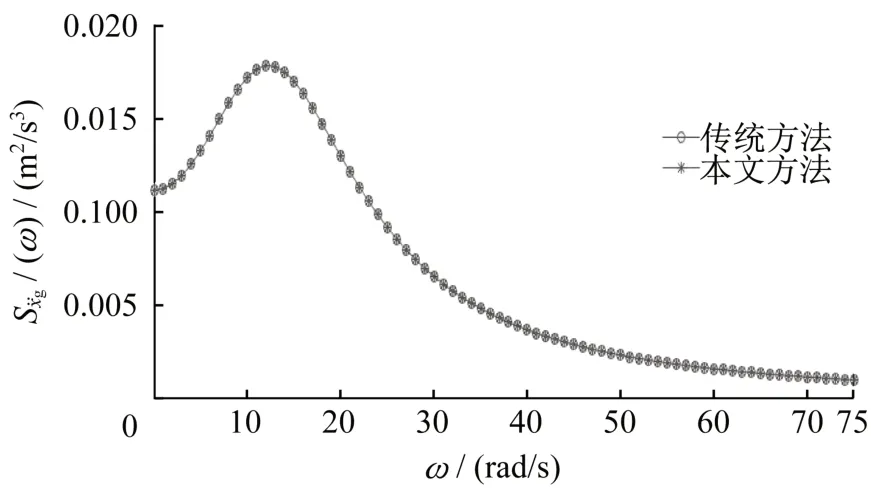
图 2 对比图Fig.2 Comparative diagram of
从图2 可知,本文方法与传统方法的功率谱完全一致,说明本文方法的正确性,但本文方法比较简洁,且容易获得谱矩的解析解,为动力可靠度分析提供了新途径。
4.2 结构位移、隔震层位移的谱矩及均方差
利用式(34)-式(37)、式(43)-式(44),可获得结构位移、隔震层位移的0~2阶谱矩及均方差,见表2。
从表2,可知ψ列的数值相对于一阶谱矩的计算结果小很多,且为复数值,λl,k、pk是共轭性特征,可知其结果应该为实数,为此,说明Π列的值仅为计算误差,并由此可以判断式(42)的假定是正确的,1阶谱矩的计算方法正确。由于在隔震层施加了横向的Maxwell 阻尼器,隔振层的位移为10.6 mm,结构层的位移为11.4 mm;而不设Maxwell阻尼器时的隔振层的横向位移为46.7 mm,结构层位移为48.22 mm。因此设置Maxwell 阻尼器可有效减少隔震层的横向变形。

表2 结构位移、隔震层位移谱矩及均方差Table 2 Spectrum moments and variance of displacement response for structural layer and isolating layer
5 结 论
本文就隔震混合耗能结构基于Kanai-Tajimi随机激励下的响应、谱矩分析方法复杂问题,提出了新的简明解法,结论如下:
(1)运用Kanai-Tajimi 随机地震动的滤波方程,混合耗能隔震耗能减震将基于Kanai-Tajimi随机地震动激励下的响应转化为白噪声激励的地震动,基于复模态法中指数运算及白噪声简明的特点,获得耗能体系的响应、谱矩的简明解析解。
(2)对于隔震结构横向设置Maxwell 阻尼器可有效减少隔震结构的水平方向位移,有效提高结构的抗震性能。
(3)本文方法为CQC 方法,所获协方差、响应、0~2 阶谱矩均具有解析表达式,可用于动力可靠度分析,并能有效提高计算效率。

