基于变刚度的组合系统的隔震性能研究

何文福 蔡 培 许 浩

（上海大学土木工程系，上海200444）

0 引 言

基础隔震技术是在建筑上部结构与地基之间采用柔性连接，设置安全的隔震系统来保护上部结构，现已成为减轻地震灾害最有效的手段之一。目前，绝大多数隔震建筑都是通过使用铅芯橡胶支座来实现隔震效果［1］，在大震情况下，铅芯橡胶支座的隔震效果不足以满足实际工程的要求。组合隔震系统利用多种隔震支座的联合来实现预期的隔震效果。因此，对于大震下的隔震结构，组合隔震系统装置可以发挥出更好的消能减震的效果［2］。

早在20世纪90年代，Kelly等［3］通过对混合控制隔震结构的研究，发现了其同时具有被动控制体系和主动控制体系的双重优点。针对于混合控制隔震结构的有效性、时滞补偿策略以及最小变异控制等问题其进行了深入地研究。Chalhoub和Kelly等［4］提出了一种基于普通橡胶支座作为复位装置的组合摩擦隔震系统，并通过振动台试验对其隔震性能进行了研究。在实现达到复位的情况下可以有效地控制结构的上部结构地震动的响应的效果。Braga 等［5］对一座低层的住宅在普通橡胶隔震和并联隔震情况下分别进行了隔震性能的研究并对比分析，其结果表明，并联的铅芯橡胶支座的隔震效果达到了设计规范的要求。Amadio等［6］通过运用有限元对框架结构模型进行了地震动分析，分析结果表明，组合的隔震系统可以有效地降低上部结构的位移以及达到消能减震的目的。Karavasilis 等［7］提出了在钢结构的框架中辅以一种特制的弹性阻尼器并用修正的力学模型，其复合隔震系统的滞回性能及隔震效果达到了预期的效果。国内关于变刚度组合隔震系统的研究相对较晚。周锡元等［8］以砌体结构为研究对象，分析得出了串联系统和并联组合隔震系统的地震动的特性，同时给出了组合配置参数以及优化设计方案。杨树标等［9］通过对橡胶、摩擦滑移以及并联组合隔震结构的隔震性能进行研究分析，得出了合理的设计与配合，可以使复合隔震体系更好地发挥隔震效果。吕西林等［10］针对并联复合隔震系统，对房屋模型进行了振动台试验研究，其结果表明，复合隔震体系具有更为有效的隔震效果以及普通隔震体系不可比拟的优越性。阎维明等［11］设计了一种半主动控制变刚度装置，并进行了振动台试验研究，结果表明，结构的加速度峰值以及位移峰值都得到了有效的控制。杨润林等［12］提出了一种半主动变刚度（ISAVS）新型控制系统，并通过数值模拟分析，得出了其结构震动控制的有效性和可行性。李轩等［13］设计一种新型摩擦滑移组合隔震系统，运用有限元软件分析得出附带少量厚层橡胶支座和黏滞阻尼器的摩擦滑移支座有效地减小了地震后的残余变形以及隔震层的最大位移。负刚度装置可以有效地降低隔震层的水平刚度，增加隔震层的柔性，地震荷载作用下结构的上部结构的层间位移、层间剪力以及加速度响应均实现同步减小，极大地提高了隔震效果。将负刚度装置与普通的隔震装置并联使用，不但其连接方式简便，且隔震效果也可得到提升。

针对于目前的隔震组合支座研究还处于初级研究阶段，并未运用在实际工程中。本文提出了一种变刚度装置［14］，通过建立变刚度装置的力学模型，并对其性能影响参数进行分析，最后通过有限元软件建立实体框架模型，对由该变刚度装置和普通橡胶隔震支座的并联组合，分别在不同工况下对动力响应进行分析，并与普通隔震系统的隔震效果进行对比分析，以此验证组合隔震系统的有效性。

1 变刚度隔震装置构造设计

1.1 变刚度隔震装置

本文提出了一种刚度随着结构位移发生改变而变化的隔震装置。该装置在当两块固定板发生相对位移时，通过两根刚性杆件压缩或者拉伸固定在连接板上的刚性弹簧，随着刚性杆件连接的刚性弹簧的压缩与拉伸，从而导致该装置刚度随之变化。

该装置由左侧连接板、右侧连接板、固定支座、刚性杆件、滑动摩擦板以及刚度弹簧组成。该新型变刚度隔震装置构造示意图如图1所示。

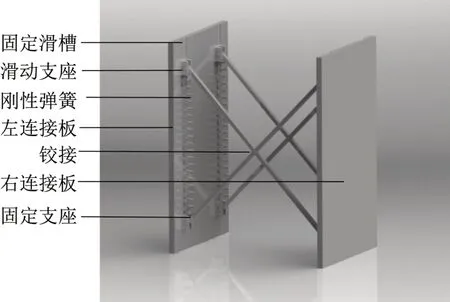
图1 变刚度隔震装置示意图Fig.1 Schematic diagram of variable stiffness isolation device

1.2 力学性能分析及力学模型

该装置的弹簧刚度为k，上部结构作用通过橡胶支座在装置上的作用力为Fh，未受荷载作用下刚性杆件与左右连接板的初始夹角为α，刚性杆件的长度为l，在荷载作用下，装置的相对位移为Δh，作用力下刚性弹簧的压缩量为Δl，θ为刚性杆件与连接板所成的锐角。在荷载作用下时，该装置具有很好的变形能力，并且可以保持稳定的较小的刚度变化，进一步保证了隔震支座的组合使用的稳定性与可靠性。该变刚度隔震装置受力变形示意图，如图2所示。

根据几何关系进行受力分析，如图3 所示，可以得到水平作用力Fh与刚性杆件的轴力FN的关系。

由图3（a）得，根据铰接点的受力平衡可以得出：

图2 变刚度隔震装置受力变形示意图Fig.2 Force deformation diagram of variable stiffness isolation device

图3 受力分析图Fig.3 Stress state

同理，由图3（b）可得，对下部滑动支座受力分析可得：

由式（1）和式（2）并根据滑动支座的受力平衡可以得出由弹簧产生的反力Fv与水平荷载Fh的关系：

式中，FN为荷载力作用下刚性杆件所产生的轴向力。

根据几何关系可以得出，该装置水平位移Δh和夹角θ以及Δl和夹角θ的关系式，分别如式（4）和式（5）所示：

式中：α为装置未受作用力初始状态下刚性杆件与连接板的夹角；Δl为在作用力下刚性弹簧的变形量。

根据Fv=k·Δl可以得出：

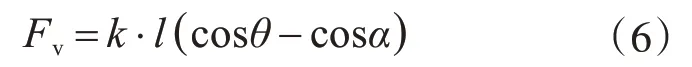
从式（3）和式（6）可以得出水平力Fh，即式（7）所示：

式中，Kh表示该装置的水平刚度。

由式（9）可得：该装置的水平刚度Kh与水平刚度k和刚度系数η有关。

根据式（4）和式（7）可以得出：

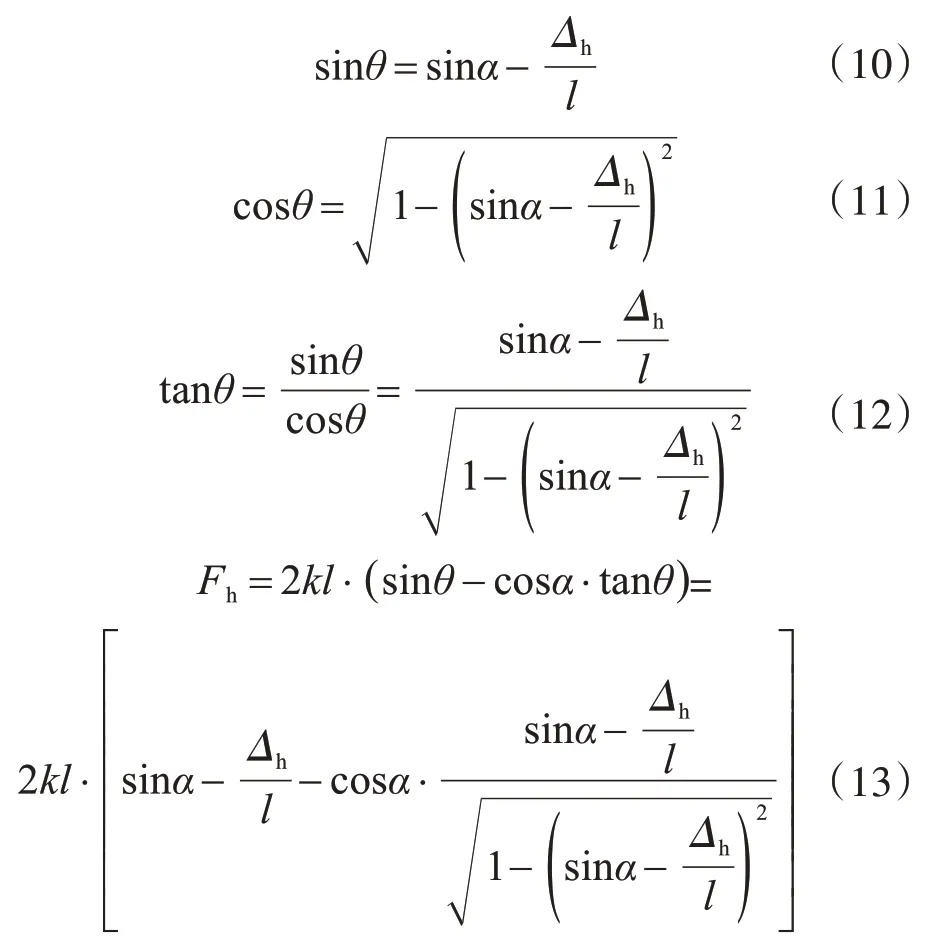
根据式（13）可以得出水平作用力与位移的函数关系，进一步可以得出该变刚度装置的力学模型，如图4所示。

图4 变刚度装置的力学模型Fig.4 Mechanical model of variable stiffness device

由图4 可得出装置在初始变形时，该变刚度装置在一定区间内提供了一个正刚度，随着位移逐步增大，该装置进入了准零刚度区间，位移进一步增大，该装置的刚度由准零刚度进而转变为负刚度。由变刚度装置的力学模型可知，我们可以通过压缩该变刚度装置使其处于负刚度区间。由提供负刚度的预压缩变刚度装置与铅芯橡胶支座并联来达到优化减震的效果。该组合隔震系统由普通的铅芯橡胶支座以及两个预压缩变刚度隔震装置并联而成，并联示意图如图5 所示。该组合隔震系统的隔震力学模型如图6所示。

图5 变刚度隔震组合系统装置示意图Fig.5 Schematic diagram of variable stiffness vibration isolation device

1.3 变刚度隔震组合系统的隔震原理

由图6 所知，利用变刚度装置的负刚度阶段与铅芯橡胶支座并联的隔震系统，既而会放大隔震层的位移响应，却可以有效减小上部结构的地震动响应，因此对隔震组合系统的负刚度部分附加阻尼以此来达到减小隔震层位移的目的，实现同时减小隔震层位移响应和上部结构地震动响应。

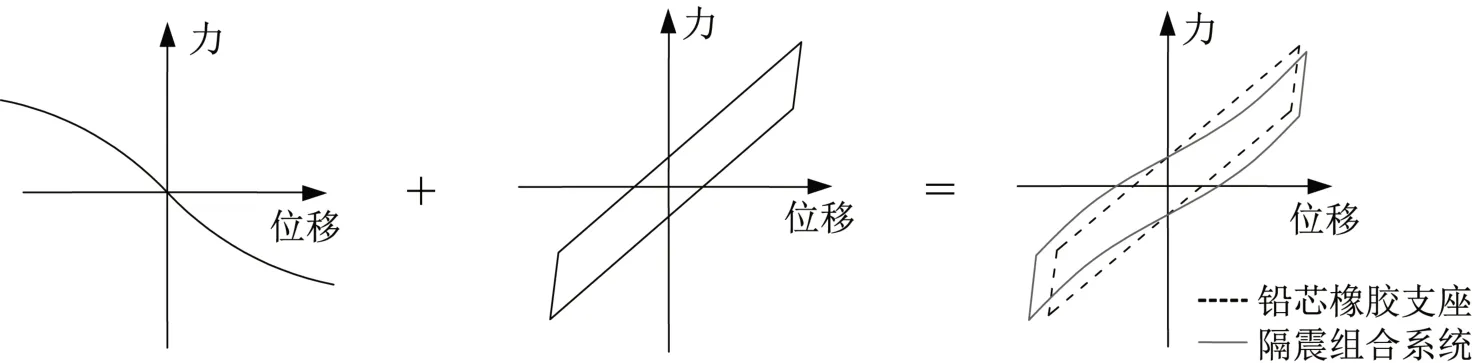
图6 变刚度隔震组合系统的力学模型Fig.6 Mechanical model of variable stiffness vibration isolation composite system

2 力学参数分析

由式（13）可以得出，该变刚度装置的刚度主要受三个参数影响，分别是弹簧的刚度k、装置的刚性杆件的长度l以及杆件与挡板的初始夹角α。下面就三个参数对水平力的影响分别进行分析。

2.1 刚度与弹簧刚度k的关系

不同弹簧的刚度k对该装置的刚度的影响差异较大，根据式（13）可以得出不同弹簧刚度k与该装置刚度的关系曲线，如图7所示。

由图7 可知，当初始夹角和刚性杆件的长度为一定值时，弹簧的刚度越大，该装置前期所提供的正刚度就越大，而达到准零刚度的位移并无明显变化，位移进一步增大时，刚度越大的弹簧所提供的负刚度也越大。

图7 变刚度与弹簧刚度的关系Fig.7 The relationship between variable stiffness and spring stiffness

2.2 刚度与刚性杆件长度l的关系

根据式（13）可以得出，不同的刚性杆件长度对变刚度的差异影响，进一步分析得到变刚度与刚性杆件的长度关系，如图8所示。

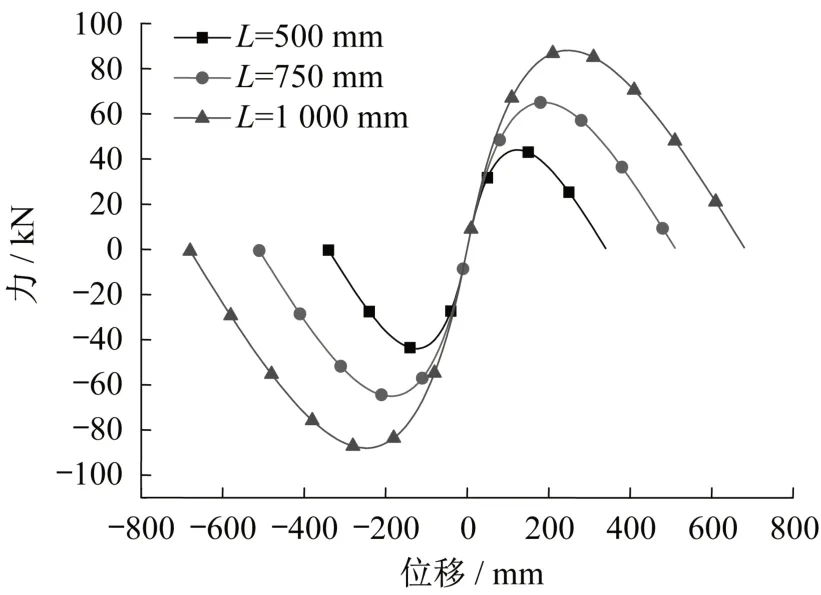
图8 变刚度与刚性杆件长度的关系Fig.8 The relation between variable stiffness and length of rigid member

由图8 可知，当弹簧的刚度和初始夹角为一定值时，刚性杆件的长度越大，该装置所达到准零刚度的位移就越大，同时长度越大的杆件，所提供的回复的力也越大。

2.3 刚度与初始夹角α的关系

不同的初始夹角α对该装置变刚度的影响也有很大差异。由式（12）和式（13）根据不同的初始夹角α可以得出与变刚度的关系，其关系曲线如图9所示。

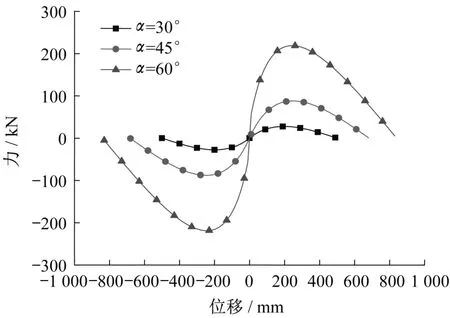
图9 变刚度与初始夹角的关系Fig.9 Relation between variable stiffness and initial included Angle

由图9 可知，随着所设的初始夹角的增大，该变刚度装置的刚度是随之增大的；且不同的初始夹角不影响变刚度达到准零刚度的位移范围。

3 组合隔震系统的地震响应对比分析

对某工程建筑进行隔震设计，通过使用有限元软件对框架结构建模，并进行了动力时程分析。将传统的铅芯橡胶支座（LRB）和采用本文提出的组合隔震系统（附带阻尼）进行了对比分析，并探讨了它们对地震响应的结果以及隔震效果。

该工程的建筑总面积约3 413 m2。此建筑共6 层，结构总质量 3 551 t，建筑面积约 1 604 m²。拟建建筑工程重要性等级为二级，抗震设防烈度为8 度，场地采用Ⅱ类第三组，场地周期0.45 s 项目采用铅芯橡胶隔震支座，本工程共使用了21 个隔震支座，橡胶支座最大面压为10.18 MPa，平均面压为6.57 MPa，隔震层平面布置如图10所示。

图10 隔震支座的平面布置图Fig.10 The layout of the isolation bearing

该建筑使用了2 种规格的铅芯橡胶支座（LRB）和2种规格的普通橡胶支座（LNR），具体参数如表1所示。

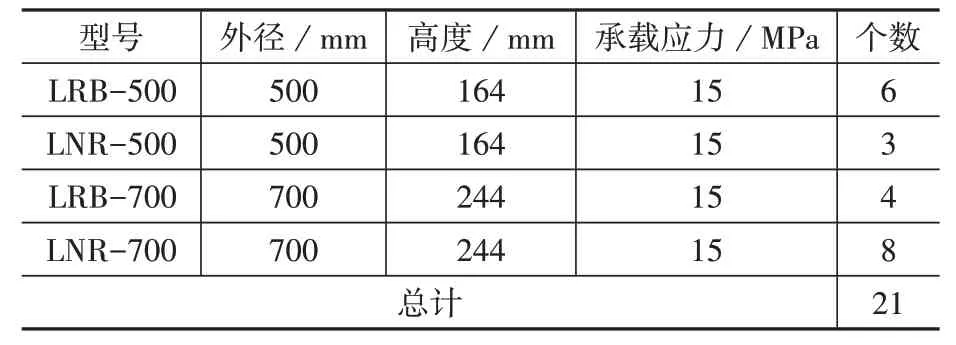
表1 隔震支座的选型Table 1 Selection of isolation support

时程分析选用了5条天然地震波，分别为Taft波、CHY050 波、Erzican 波、Rh3 波和 Rh4 波。其中，Rh3 波和 Rh4 波为人工波，Taft 波、CHY050波、Erzican波为普通地震波。图11给出了它们的反应谱曲线。结构设防烈度为8度，多遇地震输入加速度峰值为70 gal，设防地震输入加速度峰值为200 gal，罕遇地震输入加速度峰值为400 gal。地震波的输入均为双向。

表2为LRB 模型和组合隔震模型（附带阻尼）在5 条地震波作用下的楼层加速度响应峰值、隔震层位移峰值以及层间相对位移的均值对比。

图11 五条地震波的标准加速度反应谱（ξ=5%）Fig.11 Standard acceleration response spectrum of five seismic waves（ξ=5%）

从隔震层的峰值位移均值表中可以得出，当地震峰值在70 gal 时，组合隔震模型的位移减小率只有5.90%，没有明显的效果；200 gal 输入下，隔震层的减小率达到12.75%；400 gal 输入下，该组合隔震模型的位移减小率进一步增大，且减小率达到19.18%。

从加速度峰值均值的分析结果可以得到，组合隔震模型在不同的峰值地震波下，随着地震峰值的增加，其楼层的加速度峰值减小率呈现增大趋势。地震峰值70 gal 输入下，其加速度减小率最高达到20%；200 gal输入下，加速度减小率最高达到40.74%；在400 gal 输入下，其加速度的减小率最高达到45.12%。

从层间相对位移均值的分析结果可以看出，组合隔震模型在不同的峰值地震波下，随着地震峰值的增加，其层间位移的减小率也呈现出增大的趋势。在400 gal 工况下，其层间相对位移的减小率达到了51.58%。

表2 五条地震波作用下楼层加速度响应均值对比Table 2 Comparison of mean acceleration response of five seismic waves

图12 为LRB 模型和隔震组合模型在峰值400 gal 三种地震波作用下楼层加速度峰值包络图。由图可知，组合隔震模型相比于传统隔震模型（LRB）的加速度峰值都能够有效地减小。组合隔震模型的加速度响应峰值减小区间为27.52%至45.12%。由此可以得出组合隔震模型与传统隔震模型（LRB）相比较具有更好的减震效果。

图13 为LRB 模型和隔震组合模型在峰值400 gal 5种地震波作用下楼层层间位移对比。由图可知，组合隔震系统的层间位移相比于传统隔震模型（LRB）的层间位移都相应的减小。组合隔震模型的层间位移的减小区间为16.46% 至51.58%。由此得出，组合隔震模型也能够有效减小结构的层间位移的大小，从而更好地达到减震的目的。

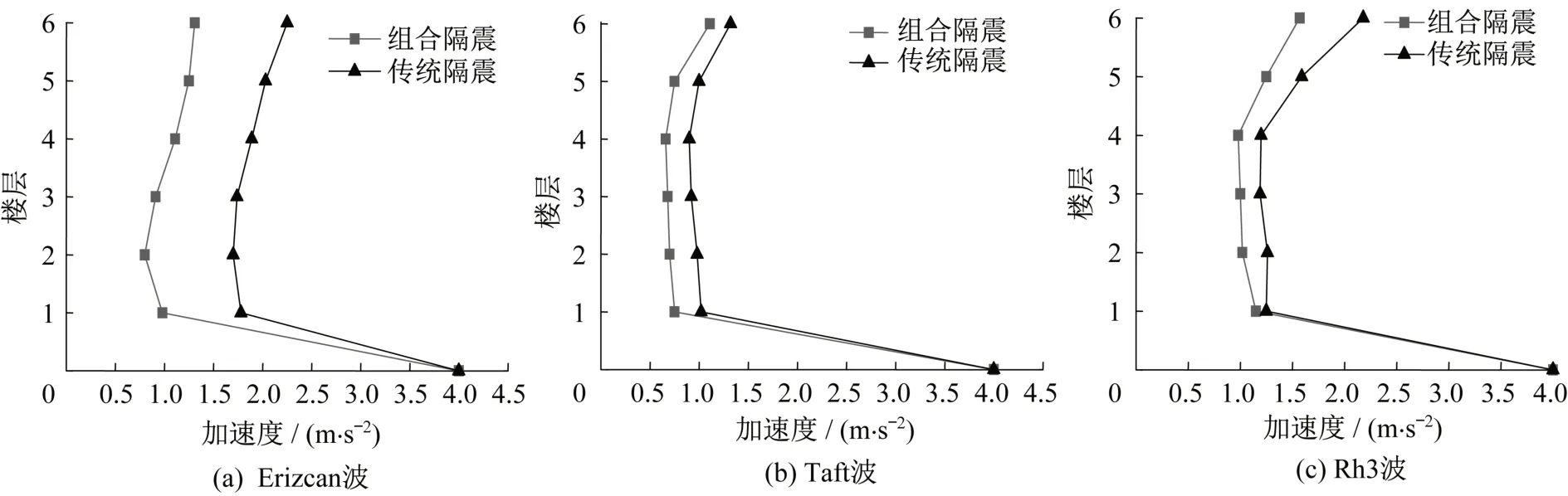
图12 峰值400 gal不同地震波作用下加速度峰值包络图对比Fig.12 Comparison of acceleration peak envelope diagram under different seismic waves at peak of 400 gal

图13 峰值400 gal不同地震波作用下层间位移对比Fig.13 Comparison of story drift under different seismic waves at the peak of 400 gal

图14 为LRB 模型和隔震组合模型在峰值400 gal 三种地震波作用下的滞回曲线对比。由图可知，隔震组合支座能够有效地减小隔震层的位移，同时其滞回曲线与LRB 模型相比更为饱满，耗能能力更为突出，隔震效果也更好。

4 结 论

本文提出了一种基于变刚度的隔震组合系统，建立其力学模型并进行了参数分析，同时对隔震结构的地震响应进行分析，对比分析了普通橡胶支座（LRB）和组合隔震支座模型的响应，得到的如下结论：

（1）提出了一种新型的变刚度装置。该装置由左右连接板、刚性杆件及刚性弹簧组成。该装置具有很好的变形能力可以很好地配合铅芯橡胶支座使用。装置在初始变形时，该变刚度装置在一定区间内提供了一个正刚度，随着位移逐步增大，其刚度进入了准零刚度区间，位移进一步增大，刚度由准零刚度转变为负刚度。

（2）通过对实际工程的框架结构进行动力时程分析，在峰值70 gal 地震波作用下，组合隔震模型的加速度响应峰值减小区间为7.84% 至20.00%；峰值200 gal 地震波作用下，组合隔震模型的加速度响应峰值减小区间为23.88% 至40.74%；在峰值400 gal 地震波作用下，组合隔震模型的加速度响应峰值减小区间为27.52%至45.12%；由此可以得出组合隔震模型与传统隔震模型（LRB）相比较具有更好的减震效果，同时也能较好地控制强震下上部结构的加速度响应。

图14 峰值400 gal不同地震波作用下隔震层滞回曲线对比Fig.14 Comparison of hysteresis loops of seismic isolation layer under different seismic waves at the peak of 400 gal

（3）时程分析结果表明，组合隔震支座相比于铅芯橡胶支座其隔震层位移最大减小率达到19.18%，上部结构的层间位移最大减小率达51.58%，其隔震减震的效果较为明显。