整体式止屈器数值模拟方法与优化研究

颜铠阳，余建星，余 杨，韩梦雪，许伟澎，张春迎

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072; 2. 天津大学 天津市港口与海洋工程重点实验室，天津 300072)

海底管道是海洋油气系统不可或缺的部分，被誉为海洋油气系统中的“生命线”，海底管道运输是一种安全性高、经济性好以及对环境危害小的运输方式。管道长期处于高压环境下，所处外部环境十分复杂，即使在铺设过程中没有发生任何损坏，但在实际服役期间，管道可能会由于受到其他物体的碰撞，产生局部的凹坑缺陷，或是由于磨损、腐蚀产生局部壁厚的减小[1]。上述各种情况都会导致管道局部上抗屈曲性能的减弱，管道在这些局部缺陷处极易发生屈曲压溃。这种局部上的压溃变形会导致相邻区域的管道也发生压溃，使压溃变形沿管长方向快速传播，引发海底管道大范围的破坏，这种现象称为屈曲传播[2]。对于深水海底管道，一旦发生屈曲传播，传播的速度可以达到数百米每秒，造成的损失无法估量，如海底管道压溃后破裂会造成石油泄漏事故，经济上和生态环境上都会是巨大的灾难[3]。

海底管道的屈曲传播特性会导致管道大面积的破坏，带来巨大的经济损失。增大管道的壁厚可以加强管道的抗压能力，使管道不那么容易压溃[4]。但是，增大管道的壁厚意味着需要增加原材料的使用量，增加了生产成本；从铺设管道角度来看，管道悬跨段的重量会随着管道壁厚的增大而增加，重量增加可能使原本使用的铺管船的张紧器能力不足，从而需要对铺管船的张紧器进行升级，进一步增加了成本[5]。因此，单凭增大管道的壁厚去解决屈曲传播导致的管道破坏问题在经济上不太可行。另一方面，若是等到屈曲传播发生后再去修复或者更换破坏的管道显然也是不可行的，因为修复或者更换海底管道的成本是巨大的[6]。

解决海底管道屈曲传播问题的一个既实用又更具经济性的方法是沿着管长方向每隔一段距离设置止屈器。止屈器的抗屈曲能力更强，如果管道发生局部压溃并产生屈曲传播，在屈曲传播到止屈器处时，止屈器可以阻止屈曲传播跨越止屈器，能使屈曲传播仅发生到止屈器处，而不再继续传播下去。止屈器的局部加强作用能够限制海底管道压溃后发生屈曲传播的范围，使屈曲传播产生的破坏止于止屈器处，保证了海底管道整体的安全性。当海底管道仅在局部发生破坏而其余部分仍完好时，管道整体的安全性不受影响。总的来说，虽然止屈器允许管道发生一定范围内的屈曲，但极大地限制了海底管道破坏失效的范围，很好地保持了管道的整体性。事实证明，止屈器的设置降低了维修管道的难度和所需时间，同时有效减少了经济损失，提高了海底管道的服役年限；另一方面，装置止屈器并不困难，成本不高，在安全性和经济性间取得了一个比较良好的平衡[7]。

按照安装形式的不同，海底管道止屈器的主要类型包括：扣入式止屈器、缠绕式止屈器、焊接式止屈器和整体式止屈器。整体式止屈器在工程中应用比较广泛[8]。

整体式止屈器是在管道铺设之前，按一定布置间距焊接在管道指定位置处的厚壁圆环，所以止屈器的内径和管道的内径相同，只是止屈器的壁厚比管道的壁厚大。止屈器和管道同轴排好之后在连接处进行焊接，如图 1所示，止屈器和管道形成一个整体，黑色三角为焊接处。

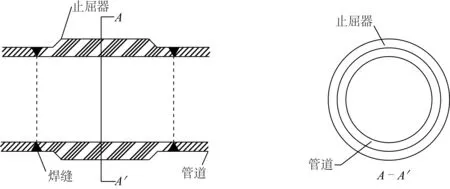
图1 整体式止屈器示意Fig. 1 Integral buckle arrestors

止屈器可以阻止屈曲的传播，但是当外部水压高于一定的数值时，屈曲传播还是会“穿越”止屈器继续向下游传播[9]，屈曲能够穿越止屈器继续向下游传播时对应的外部水压压力值称为止屈器的穿越压力Px。

关于止屈器的止屈效果和穿越压力，国内外学者进行了诸多研究。Park等[10]进行了整体式止屈器的穿越试验，分析止屈效果与长度、厚度等变量之间的关系。Mansour等[11]采用有限元方法对整体式止屈器进行了准静态和动态试验条件下穿越压力的计算，并与试验结果进行对比。Toscano等[12]通过试验和数值模拟的方法，研究了整体式止屈器的穿越模式，取得了较为一致的结果，这表明有限元模型可以对止屈器性能进行较好的预测。Dyau等[13]运用模型试验和数值模拟的方法，研究了扣入式止屈器和整体式止屈器的工作性能，分析了止屈器的长度、壁厚和材料性能等参数对止屈器穿越压力的影响。Kamil等[14]使用有限元分析软件ANSYS，对安装整体式止屈器的海底管道进行仿真模拟，分析了管道壁厚、径厚比、止屈器长度以及管道外径4种几何要素的变化对整体式止屈器止屈效果的影响。

进行模型试验能够比较真实地反映研究对象发生作用的全过程，得到的结果比较准确，但是进行模型试验所需的材料成本和时间成本大，每次研究都进行模型试验是不现实的，特别是整体式止屈器试验过程复杂，无法进行大量模型试验。而随着科学技术的发展以及有限元分析方法的完善，现在可以使用各种有限元分析软件进行仿真模拟，并且仿真模拟的结果具有较强的科学性和准确性，计算得出的数值比较接近实际情况，有限元数值模拟已经成为一种常用的研究方法。因此，利用ABAQUS软件建立相应的有限元模型，并且改变管道和止屈器的重要设计参数，进行系列计算，以便进行整体式止屈器的优化。

1 计算方法

1.1 广义弧长法

深水海底管道的屈曲传播与止屈涉及较复杂的非线性问题，主要包括：①管道发生屈曲传播时，钢材已经进入塑性变形阶段，这属于材料的非线性问题；②在管道压溃继而发生屈曲传播的过程中，管道的截面会发生大变形，这属于几何非线性的问题；③在压力作用下，管道内壁最终会相互接触，接触分析属于典型的边界条件非线性问题。

上述3个非线性问题导致整个管道止屈器系统发生极值失稳后的荷载-位移路径非常复杂，必须选择合适的方式控制增量步长，才能追踪荷载-位移的变化路径。非线性分析中一种比较常用的方法是广义弧长法，即通过在ABAQUS中step模块下选择Static，Riks类型的计算方法，设置相关参数进行求解。

这种计算方法是将施加的荷载也作为一个变量来求解，所以它的荷载增量步是变化的，但这相当于给原来的求解方程组增加了一个未知量，要求解方程组就需要再补充一个控制方程。这个控制方程形式上是一个圆的方程，它的圆心是上一个荷载步的收敛点，半径则与上一个荷载步得到的荷载和位移有关。有了这个补充方程，就可以继续往下求解。因为补充的方程是一个圆方程，说明使用这种计算方法的迭代路径是一个圆弧，所以称为弧长法；另一方面，该方法需要同时求解荷载和位移，属于一种广义的位移控制法，所以称为广义弧长法。

使用这种计算方法具有操作简单易上手的优点，只需要在ABAQUS中step模块下设置相关参数即可。下面结合ABAQUS操作界面和外部INP文件解释相关参数。

INP文件中该部分相关的代码如下。

**STEP:Step-1

**

*Step,name=Step-1,nlgeom=YES,inc=

*Static,Riks

Δlinit,lperiod, Δlmin, Δlmax,λend, node, dof,μmax

*END STEP

在ABAQUS中创建分析步，设置分析步名称，即“Step, name=Step-1”；类型选择“Static，Riks”；设置Nlgeom的参数为on，即“nlgeom=YES”；“inc=”后的数值表示进行分析的步数的最大值；“Static,Riks”后是数据行，并不要求填写列示的所有参数，这些参数的定义分别为：

Δlinit和lperiod两个参数定义分析步中与求解方程相关的初始弧长和总弧长；

Δlmin和Δlmax两个参数组成弧长增量的上下界限；

λend、node、dof和μmax四个参数用于设置分析的终止条件，λend表示荷载超出某一数值则终止分析，node, dof,μmax表示设置一点的位移分量超出某一数值则终止分析。

可以看出，初始的操作设置十分简单，完成之后便交给计算机求解；但要使设置的弧长能够有效地求解计算却不容易，一个不成功的弧长设置会导致荷载-位移曲线原路返回，此时需要调整参数再次尝试。

使用广义弧长法进行了8次计算，其中比较典型的错误情况包括出现“回漂”现象以及计算到止屈器部分不收敛现象。

图2展现了出现“回漂”现象时模型的荷载比例因子随弧长变化的曲线。荷载比例因子是模型所受静水压力与模型中预设压力值的比值，弧长与增量步数正相关。值得注意的是，曲线在出现第一个峰值点后开始下降，而在工程实际中，在产生压溃后，屈曲开始传播，此时压力减小且维持稳定，直到屈曲传播到止屈器部分，由于止屈器的结构强度更大，屈曲若想穿越，则需要更大的压力，这个压力便是止屈器的穿越压力。图 2曲线连续下降，荷载比例因子持续减小甚至出现负值，说明外部水压力一直减小甚至从外压变成了内压，这显然是不符合实际的。“回漂”现象出现在屈曲还未传播到止屈器部分时，往前计算不能收敛，往回计算可以收敛，于是出现了屈曲往回传播的现象，这种情况下便无法得到止屈器的穿越压力。

另外一种情况是屈曲成功传播到止屈器部分，计算过程中没有产生“回漂”现象，此时管道受到的静水压力逐渐增大，但随着压力的增大，到达某个压力值时，计算不再收敛，最后报错，如图3所示。查看变形云图可知报错的点在止屈器穿越压力点附近。出现这种情况的原因可能是因为止屈器部分的结构比较复杂，在止屈器部分容易计算不收敛。

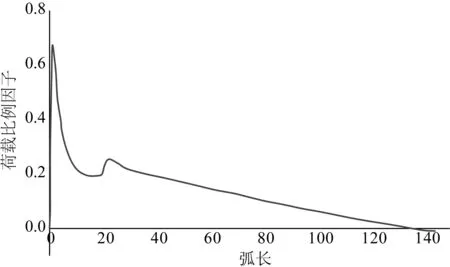
图2 “回漂”现象Fig. 2 Failed cases-drift back

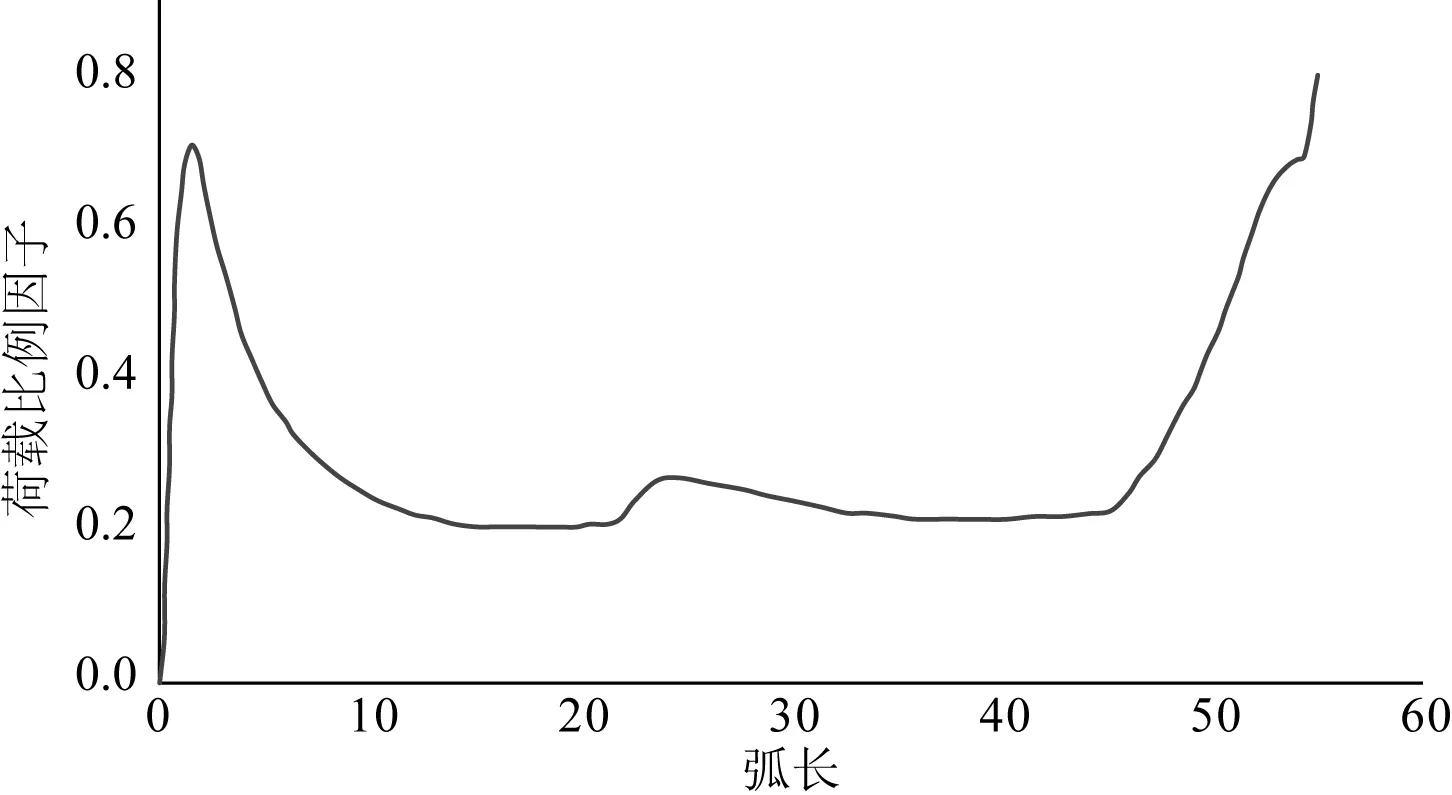
图3 止屈器附近报错Fig. 3 Failed case-aborted

总而言之，使用广义弧长法计算管道止屈器模型，往往需要经过多次尝试，得到适当的弧长搭配，最后才能得到需要的结果。

由于文中需要建立多组模型，使用广义弧长法显然会给研究带来很大的不确定性和不便利。对此，使用另一种计算方法来解决这个麻烦的问题——静水流体单元法。

1.2 静水流体单元法

静水流体单元(F3D4)又称流体弹簧单元，是在空间上由若干个表面形成一个空腔，在指定的参考点上与受载结构外表面耦合，从而由结构变形情况确定空腔的体积变化，进而确定作用于结构上流体压力的大小。静水流体单元可以用来确定在结构物周围定义的某个控制区域内的体积变化，于是将压力控制加载转变为体积控制加载，而压力的大小可以通过体积的变化来计算。所以，静水流体单元法采用的是一种特殊体积控制加载方式，这种加载方式可以很好地模拟管道模型在水压作用下的屈曲传播以及屈曲穿越止屈器，不会出现广义弧长法中的“回漂”现象和计算不收敛的问题。

使用广义弧长法计算管道止屈器模型会出现各种问题是因为分析海底管道此类结构的一个难点在于物体的变形与流体的压力之间有耦合作用。这种耦合作用，使得结构的变形大小不只取决于外部施加的荷载，还取决于流体的压力，而流体的压力又会受到结构变形的影响。安装止屈器的管道结构更加复杂，所以，不只是计算管道受到的压力有困难，成功求得止屈器的穿越压力更加困难。ABAQUS提供的静水流体单元是一种能够提供结构变形与内部流体压力变化之间耦合作用的表面单元，它可以用来模拟被流体充满的腔体结构，这种结构的响应不仅取决于外部的载荷，还与内部流体的压力变化有关，而内部流体的压力变化又会受到腔体变形的影响。静水流体单元能提供这种结构变形与内部流体压力变化之间的耦合作用。

静水流体单元是一种覆盖在腔体边界上的表面单元，它与腔体内边界共享节点，对所有的静水流体单元必须定义一个共享的参考点，这个参考点是用来计算腔体体积的，从而来反映腔体内部流体的压力，所以参考点的位置是个关键问题。如果腔体结构不是对称的，参考点必须能够完全被静水流体单元包围成一个封闭的区域，此时参考点的位置是任意的，不一定要在腔体内部；如果腔体结构是对称的，通常选择只建立一半模型以简化建模过程，此时参考点必须位于对称轴或对称面上，若具有多个对称面，参考点应位于对称面的交点上。

静水流体单元的参考点可以设定一个代表压力的自由度，参考点的压力自由度是主要的变量。因此，可以通过定义模型的边界条件来设定参考点的自由度，这和在结构上设定节点位移的方法是类似的。为参考点设定压力等效于在腔体边界上作用统一的分布载荷。如果对参考点设定了压力的自由度，还需要定义一定的流量q来表示流体注入与排出腔体，q值为正代表向腔体内流入，q值为负代表水从腔体排出。正如流体可以根据压力的变化自动注入或排出腔体，流体的体积也会相应的自动调整以保证充满腔体。最后通过设置两个变量PCAV和CVOL得到流体的压力与流体体积的历史输出。

具体的操作就是，管道以及止屈器模型依然使用标准的有限元单元模拟，然后在整个模型外面建立一个流体舱，接着在流体舱与管道止屈器模型之间设置静水流体单元，这就相当于往流体舱内“注水”，直到达到预先设置的流量值。也就是说，可以控制注入流体的量，只要注入的“水”足够多就能够将管道完全压坏。所以，不会出现广义弧长法中由于弧长设置不当导致的无法计算出穿越压力的情况，因为可以通过注入足够多的“水”将管道压坏，也就可以得到需要的穿越压力值。

2 数值模拟

海底管道的屈曲传播与止屈涉及较复杂的非线性问题，现在还难以建立有效的力学模型求得精确的解析解，因而采用ABAQUS软件建立三维有限元模型来模拟海底管道屈曲压溃、屈曲传播和屈曲穿越止屈器的全过程，并计算结构临界失效压力。由于焊缝的影响不是文中研究的重点，并且焊接工艺的成熟使得焊接处比较稳定，因此，模拟中将管道和止屈器设置为一个整体，不考虑它们之间的边界约束。

在均匀外部压力作用下管道的受力变形具有对称性，同时模型具有几何对称性，因此，将x=0、y=0和z=0三个平面设置为对称面，建立1/4的管道模型，以简化建模过程，加快建模速度，提高计算效率。

模型材料的本构关系，可通过进行材料的力学特性试验得到。具体的方法是在管件上裁剪试验片来做单向拉伸试验，并利用拉伸试验测量得到的数据，使用Ramberg-Osgood方程来对这些数据进行拟合，最终拟合得到材料屈服应力-塑性应变曲线，求得材料硬化参数n与屈服应力σy。材料属性如表 1所示。

表1 材料属性Tab. 1 Material properties

采用流体加载的方式模拟海底管道的屈曲发生以及传播的整个过程，关键在于引入静水流体单元。在管道外部建立一个轴向长度相同、半径为D的流体舱，同时需要在管道止屈器模型的外壁建立一层Skin单元，这样才可以在流体舱与管道之间连续加入静水流体单元，模拟注入“水”以增大管道外部压力，如图 4所示。注意选择Skin单元的方向，需要使管道止屈器的外壁以及流体舱的内壁处于激活(positive)状态，流体舱的外壁处于未激活(negative)状态，才能在其间注入静水流体单元，以提供管道所受外部压力，而管道内部不存在压力。

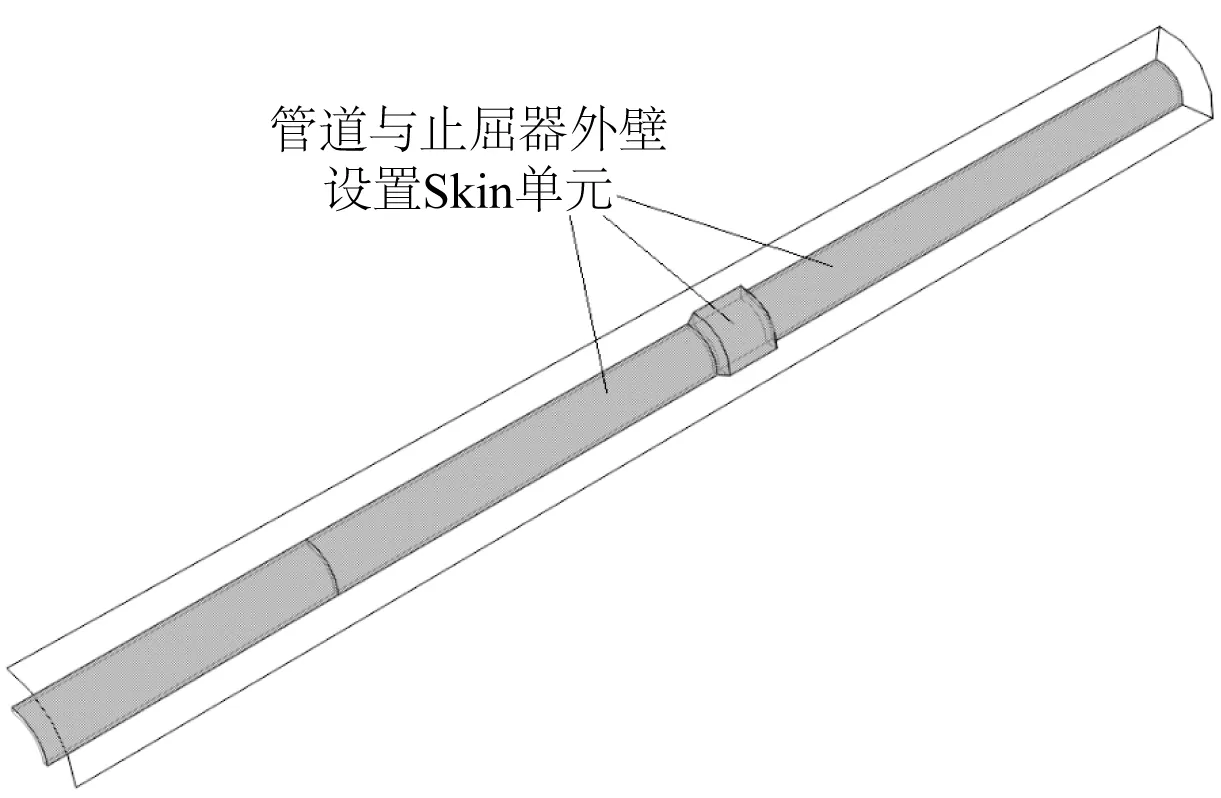
图4 设置Skin单元Fig. 4 Skin manager

关于网格划分，一方面需要尽可能减少网格的数量以提高计算速度，另一方面要保证计算的精确度，因此，管道、止屈器以及流体舱的周向上划分为15～20份，管道以及止屈器的径向上划分为1～2份，管道的轴向上按每D个单位长度划分为10份，但在管道与止屈器的接触部分进行网格的加密处理。网格单元类型方面，管道和止屈器部分选择八节点六面体线性非协调模式单元(C3D8I)，流体舱选择有限薄膜应变线性减缩积分壳单元(S4R)，后续在INP文件中将其修改为静水流体单元(F3D4)，如图 5所示。

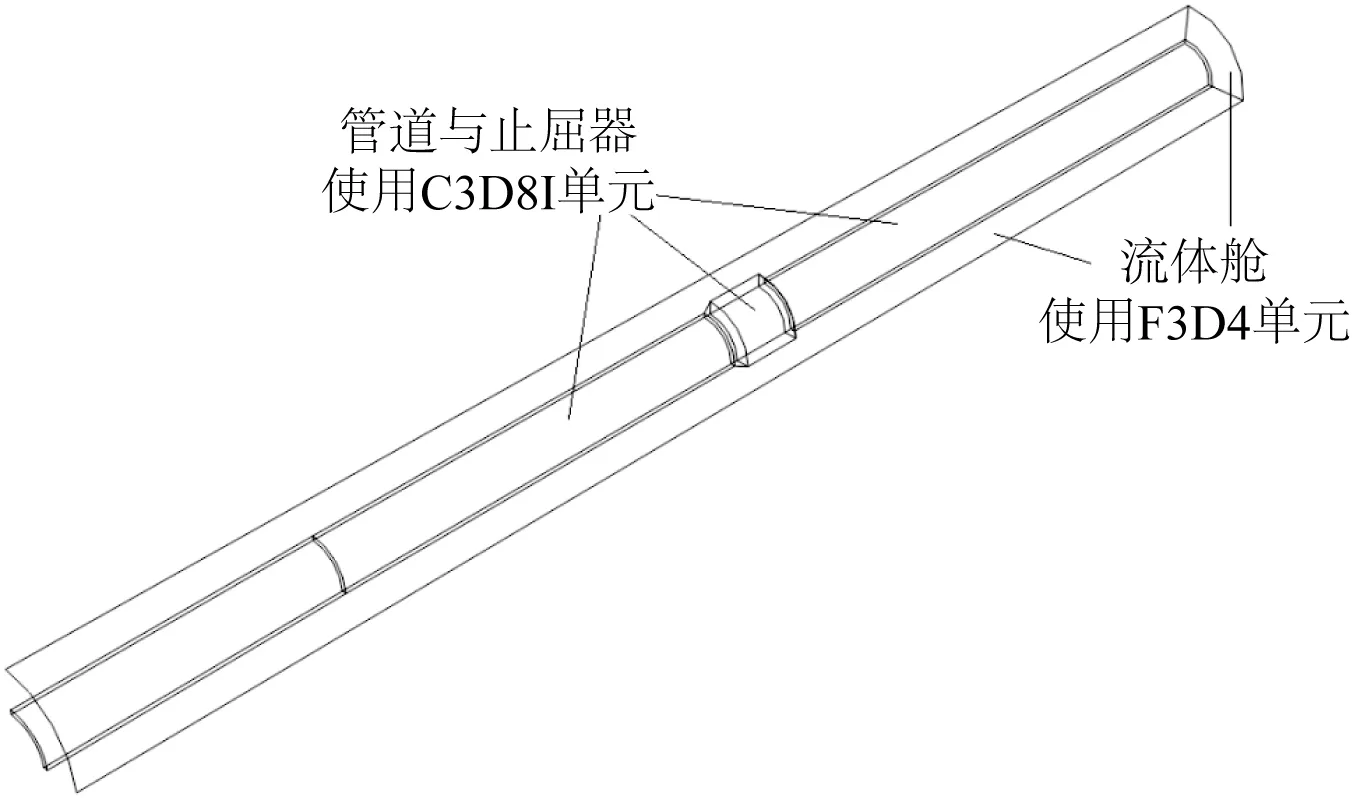
图5 模型示意和使用单元Fig. 5 Finite element model and element type

管道止屈器模型建立完毕，然后通过修改INP文件以设置静水流体单元。同时设置两个历史输出变量CVOL和PCAV，它们分别表示注入流体的体积以及模型表面受到的压力。

提交运算，结果表明该模型能够成功地模拟管道发生局部压溃、屈曲传播和屈曲穿越止屈器的全过程。如图6所示为屈曲穿越止屈器，即外界水压等于穿越压力Px时的Mises应力云图。

图6 屈曲穿越止屈器时Mises应力图Fig. 6 Mises diagram when buckle passes through arrestors

提取历史输出变量CVOL和PCAV的数据，绘制得到管道表面所受压力随着流体舱内流体体积的变化曲线，如图7所示。

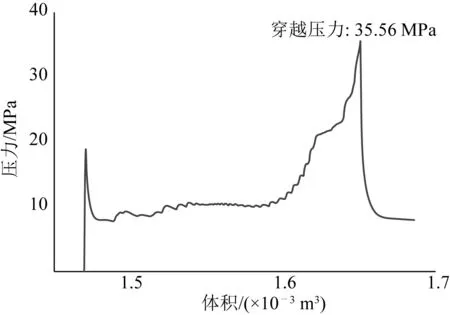
图7 压力随体积变化曲线Fig. 7 Pressure-volume curve

变化曲线可以表征整个模拟过程中管道止屈器发生的变形过程。第一个峰值表示管道在局部缺陷处，由于外界压力作用，发生初始压溃；随着管道局部缺陷处发生压溃，压力虽然迅速回落，但压溃导致的变形还是会不断发展，直到管道内壁开始互相接触；管道内壁互相接触后，变形便停止并开始稳定向下游传播，传播过程中压力稳定在屈曲传播压力附近，对应着曲线中间水平部分，该部分压力的平均值可以作为管道的屈曲传播压力；屈曲不断往下游传播，直到屈曲传播到止屈器附近，由于止屈器对屈曲传播的阻碍作用，屈曲暂时不能通过止屈器，但“水”不断注入，所以管道表面压力开始逐渐增大，最后屈曲增大到能够“穿越”止屈器并继续向下游管道传播，压力又由一个峰值陡然下降，并最终稳定在其传播压力附近，曲线中第二个峰值的数值就是止屈器的穿越压力。

可以看出，有限元模型能够准确模拟屈曲穿越止屈器的全过程，通过有限元模型计算得到的曲线符合实际。另一方面，根据文献[2]公布的数据进行了数值模拟，对比文献中公布的试验和数值模拟结果，对比结果如表 2所示。表中，D、t、La、h是试验数据，分别表示管道外径、管道壁厚、止屈器有效长度和止屈器厚度，ExperimentPx是试验得出的穿越压力，FEM1Px是文献[2]中使用有限元方法得出的穿越压力，FEM2Px是文中自行求解得出的穿越压力，结果比较接近，可以验证模型的准确性。

表2 对比结果Tab. 2 Comparative results

在止屈器试验过程复杂，无法进行大量试验的现实情况下，可以使用有限元模型对止屈器结构优化进行分析。

3 结构优化

整体式止屈器在限制深水海底管道屈曲传播方面作用显著，但传统的止屈器构型上存在材料利用率低的问题，存在进行结构优化的空间。

整体式止屈器结构横截面如图 8所示，其中，D，t，h，Ls，La分别代表管道外径、管道壁厚、止屈器厚度、止屈器总长度和止屈器有效长度。优化方案是在保证止屈效果的基础上，尽可能减少止屈器材料使用量以降低生产成本。在管道外径、管道厚度、止屈器总长、止屈器厚度不变的条件下，减小止屈器的有效长度，可以减少止屈器体积，也就减少了止屈器材料使用量。

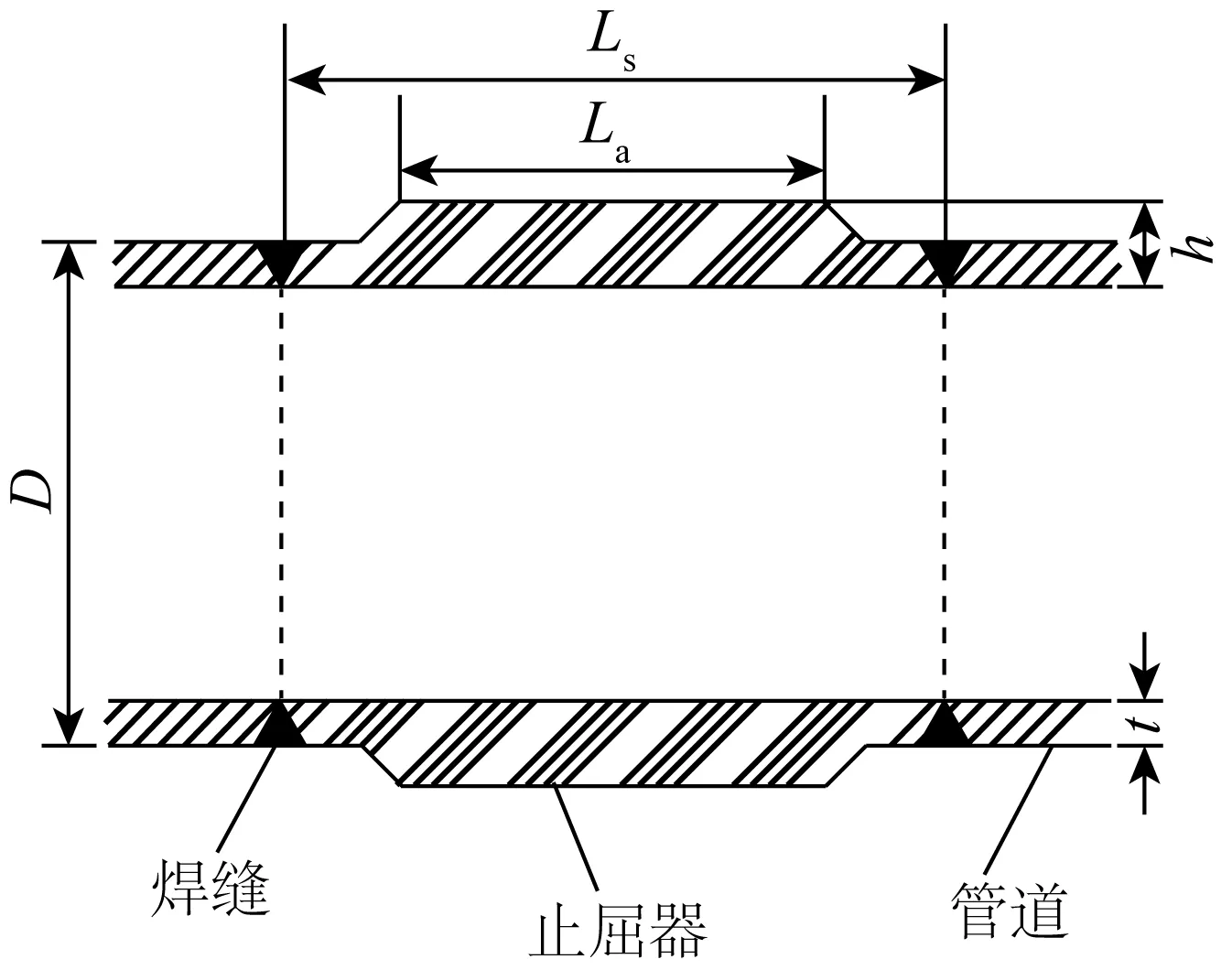
图8 止屈器横截面Fig. 8 Cross section of buckle arrestors

图9直观展现了La=49.6 mm与La=1.0 mm两种止屈器体积的对比，可以明显看出，后一种止屈器可以比前者减少许多材料。

图9 两种止屈器体积对比Fig. 9 Volume difference between two buckle arrestors

图10则展现了屈曲即将穿越过止屈器时，两种止屈器的Mises应力图。由Mises应力的分布看，有效长度为1.0 mm的止屈器，止屈器部分所受的应力基本是一致的，而有效长度为49.6 mm的止屈器，止屈器部分所受的应力并不均匀，止屈器靠近管道上游部分所受应力较大，说明这部分止屈器主要承受压力，而它的边缘部分所受应力较小，说明这部分止屈器并没有充分发挥效用，实际上是一种材料的浪费。这也说明了减小止屈器的体积进行优化是有意义的。

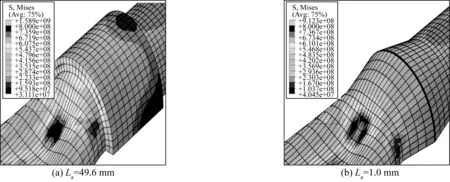
图10 两种止屈器Mises应力对比Fig. 10 Mises difference between two buckle arrestors

为了更科学地分析止屈器的体积变化与穿越压力变化之间的关系，研究该优化方法的可行性，改变止屈器的有效长度，建立了8组有限元模型，整理得到止屈器穿越压力的变化及与初始模型的变化比、止屈器体积的变化以及与初始模型的变化比。8组止屈器的穿越压力与体积的数值及变化值如表 3所示。

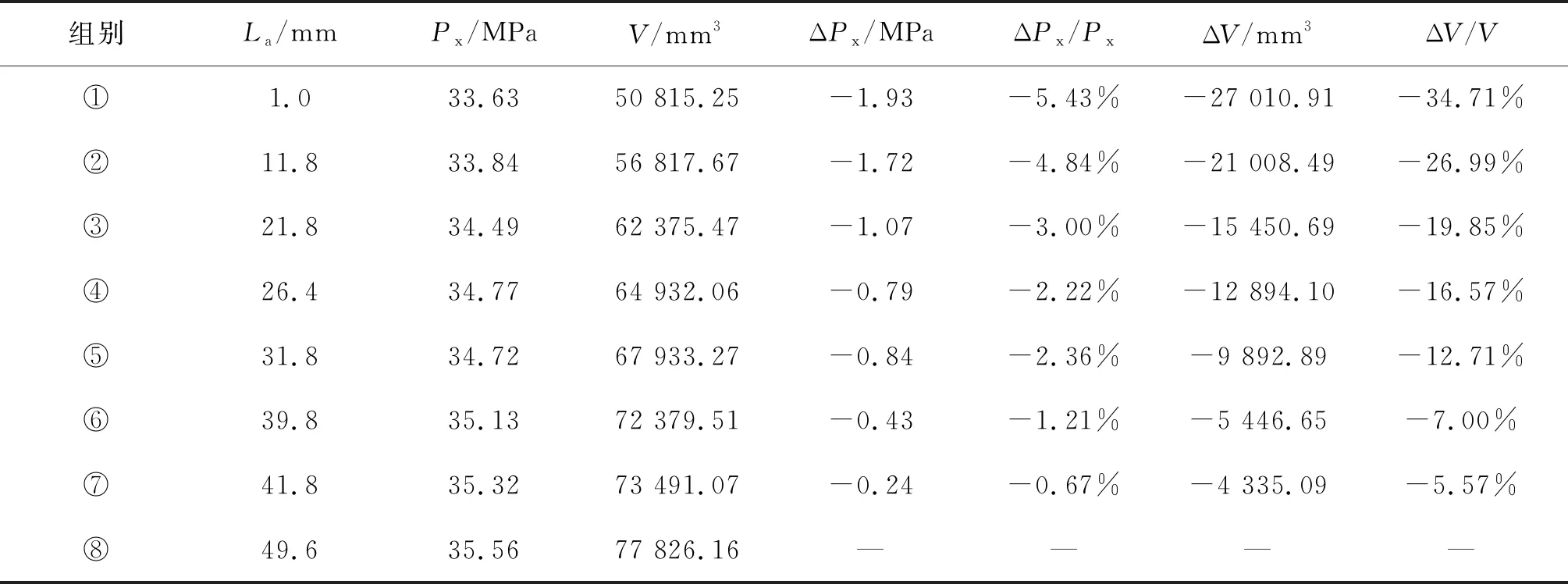
表3 各模型穿越压力与体积对比Tab. 3 Px and volume difference among models

由对比结果可知，相比于有效长度较长的初始止屈器，即第⑧组有效长度为49.6 mm的止屈器，将止屈器有效长度减小后的止屈器具备几乎相同的止屈能力，即使是对于第①组有效长度最小的止屈器，与初始模型相比，其穿越压力的损失也不超过6%，却能大大减小止屈器的体积，从而节省材料重量，最多能够节省超过30%的材料重量，使得成本大大降低。也就是说，减少止屈器体积既可以保证止屈效果，同时节省材料用量，降低生产成本，体积的减少还使得安装难度降低，有助于降低整个生产安装过程的成本，因此这种减少止屈器体积的结构优化方案具有可行性。

4 结 语

以深水海底管道系统中常用的整体式止屈器为研究对象，利用有限元软件进行数值模拟，分析了发生压溃、屈曲传播以及屈曲穿越止屈器的全过程，并以减少体积降低成本为目标，对止屈器进行了结构优化，得到以下结论：

1) 对比了广义弧长法与静水流体单元法在计算止屈器模型时的优缺点，选择使用静水流体单元法，并详细介绍静水流体单元相关内容。

2) 使用ABAQUS软件建立数值模型，对带有整体式止屈器的海底管道进行了从发生压溃、屈曲传播、屈曲穿越止屈器、屈曲向下游传播全过程的模拟，提取相关数据绘制变化曲线，其各阶段变化趋势符合实际，验证了有限元模型计算穿越压力的准确性。

3) 减少止屈器体积的结构优化方案具有可行性，能够在保证止屈能力的前提下，减少材料用量，有利于焊接、铺设等工作的开展，具有一定的应用价值。