波流共同作用下海底人工边坡动态响应分析

刘成林，陈炜昀，陈国兴，俞 缙

(1. 河海大学 港口海岸与近海工程学院，江苏 南京 210098; 2. 南京工业大学 岩土工程研究所，江苏 南京 210009; 3. 华侨大学 土木工程学院，福建 厦门 361021)

近海工程埋置型结构物(如沉管隧道、海底管道等)在建设过程中，通常需要预先在海床表面开挖一段基槽，便于建筑物埋置。这种处理方式使得建筑物能减少周围环境作用力，也避免了在不稳定的新近沉积土海床表面施工。在自然海洋环境中，海洋波浪时常与海流(比如洋流、涡流、潮汐流等)同时存在，这种波流共同作用下的荷载将进一步使海床中的孔压和有效应力产生变化[1]。在一定条件下，波流荷载下的超孔隙水压力超过土体自身的初始有效应力，相应土体会发生失稳并产生液化[2]。同时，由于海床基槽的开挖，原有海床土体在长期自然环境影响下形成的初始应力和固结状态会发生改变。因此，波流作用下的海床响应和液化评估应该基于工程扰动后的海床状态。

通常情况下，动荷载作用下的海床响应机理可以根据孔隙水压力的产生机理分为两种形式。其一是由于波浪在海床中产生孔隙水压力的相位滞后性而导致的瞬态液化，通常发生在波谷之下较为密实的海床中[3]。另一种是较为松散海床在波浪循环荷载下密实，土颗粒进行重新分布，残余孔压累积最终可能诱发液化[4]。关于两种液化发生形式和适用范围的讨论在文献[5]中有详细论述。然而，不论何种液化发生，对建设在海床上的近海工程结构物稳定性都会构成很大威胁，目前已有大量研究关注于防波堤、管线周围海床在波浪荷载下的动态响应[6-8]。由于文中主要研究的是基槽开挖后的临时海床形态受波流荷载下的动态响应，因此着重对海床的瞬态响应及瞬态液化情况进行讨论。

众所周知，海床的失稳破坏是在一定的静荷载和动荷载共同作用下发生的。其中，静荷载指海床土体自身的重力，取决于海床的几何形状和地质情况。动荷载则来自于波流作用对床面产生的动压力，与海床所处波流环境有关。近年来开展了很多关于海床动态响应的研究，包括解析解形式[5]、试验研究形式[9-10]以及数值模拟研究形式[11-12]。最近，Lin等[13]采用水平集方法[14-15]捕捉两相流中水和空气的表面，基于有限元模型分析了波浪荷载下几种特定管道埋置形式下的动态海床响应。年廷凯等[16]基于极限分析上限方法，求解了极端条件下不同时刻的斜坡海床稳定性系数。Duan等[17]采用有限元方法实现了波流-海床-管道耦合计算，计算了在基槽内部分回填管道周围无黏性土的液化情况，得到了管道回填厚度选取与波浪参数的经验公式。Liao等[18]采用两阶段耦合数值框架计算了倾斜防波堤端部周围土体的动态响应。然而，以上研究中大部分都是对未经扰动的平坦海床进行动态响应计算，对海底人工开挖基槽形成的不规则海床在波流共同作用下的响应少有研究。

为了研究开挖之后的基槽周围海床在波流荷载作用下的动态响应，建立了一个二维波流-海床耦合模型。通过雷诺时均纳维—斯托克斯(RANS)方程结合湍流模型模拟波浪场，在模型两侧边界设定稳定流速边界实现流场的模拟，海床的动态响应通过Biot多孔弹性理论计算得出。分析了基槽开挖后的海床初始应力和应变的变化情况，讨论了波浪参数及海流参数对海床响应结果的影响(包括孔压变化和液化情况变化)，以及波流耦合下的波浪形态变化。最后，提出了流速与海床液化深度的经验关系，对于近海水下基槽开挖的设计和施工提供了建议和参考。

1 数值模型与模型验证

考虑波流共同作用下开挖后的基槽海床动态响应问题，计算模型如图1所示。模型主要分为两部分，波流子模型和海床子模型。波浪部分通过求解RANS方程和k-ε湍流闭合方程实现波浪场模拟，其中通过求解包含动量源项的方程实现动量源造波。海床部分通过Biot理论得到波-流底部压力作用下的孔压和位移。在波浪传递区域的上边界定义定常流入流速，下边界设定定常流出流速和压力输出边界实现稳定的流场模拟，从而实现波流同向相互作用(如图1所示)。反之，则可以实现波流反向相互作用。

图1 模型计算示意Fig. 1 Sketch of the analysis model

1.1 波流模型

1.1.1 波浪模型

模型采用动量源函数造波，通过将动量源函数代入动量守恒公式中的源项得以实现。另外，通过水平集(LSM)方法结合移动网格方法捕捉空气和波浪两相流体的接触表面，即随时间而改变的波浪自由表面。

模型中采用求解实际应用中最为常用的标准k-ε湍流模型结合RANS方程来实现波浪场的模拟。众所周知的是，湍流是一种复杂、非稳态、旋转的不规则流动形式，由黏性力引起。k-ε湍流模型主要包括两个输运方程和两个独立变量：湍流动能k和湍流耗散率ε。湍流黏度表示为：

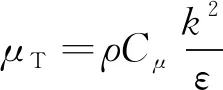
(1)

其中，ρ为流体密度，Cμ表示一个湍流模型参数。

湍流动能k的输运方程可表示为：

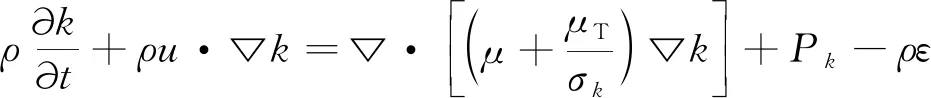
(2)

耗散率ε的输运方程表示为：

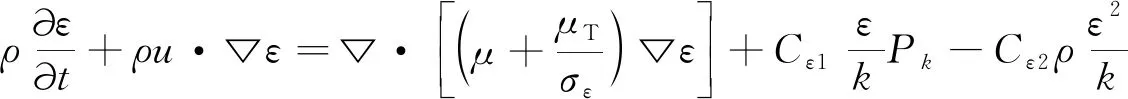
(3)

上述方程(1)～(3)中的模型常数Cμ，Cε1，Cε2，σk，σε分别为0.09，1.44，1.92，1.0，1.3[19]。方程(2)～(3)中Pk表示湍流压力分布项。

由于模型考虑的为二维问题，故质量守恒方程和动量守恒方程可以表示为：

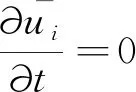
(4)

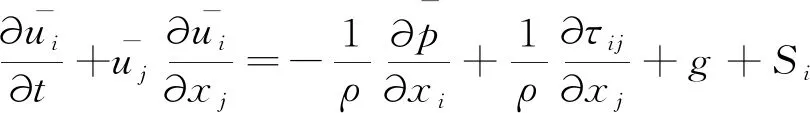
(5)

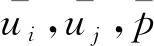
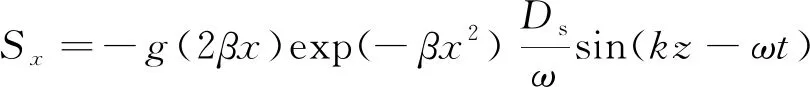
(6)

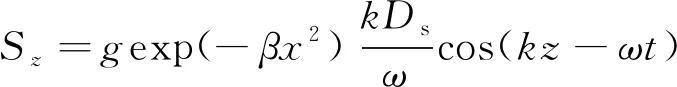
(7)

其中，k为波数；ω为波浪角频率；β=80/(δ2·L2)为造波源区的宽度，其中L为波长并且δ为表征造波宽度的一个参数；Ds为源区的振动幅度。更多动量源造波的介绍可参考Wei等[20]，Choi和Yoon[21]的研究。

模型中采用水平集方法(LSM)捕捉空气和波浪两相流的接触面，即波浪表面。相关公式可以表示为：

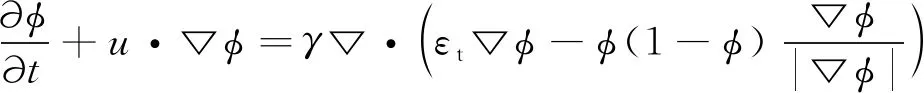
(8)

其中，φ为水平集函数；εt是控制两相流界面厚度的参数，其默认值为跨越两相界面处网格最大尺寸的一半；γ是重新初始化的参数；u为流速场的速度分量，采用的流速通过对流的方法实现水平集参数的读取。关于水平集方法在Desjardins等[22]的研究中有详细介绍。

1.1.2 海流模型

在数值波浪传递区域的上侧边界设定稳定的流速入口，在下侧边界设定稳定的流速出口，可以实现波流同向传递。反之则可以实现波流反向传递。法向流速设置为u=-nU0，其中n表示流入/流出边界的法向向量，U0为稳定海流的速度。

1.2 海床模型

由于模型主要研究的工况为基槽开挖完毕的临时工况，波浪作用于海床断面的时间较短，因此文中主要关注于土体的瞬态响应。通常，沉管隧道的天然海床基础可视为多相介质材料，包括固体相(土骨架)、流体相(水和气体)。二维海床模型的建立采用Biot固结方程(“Q-S方程”)，由Biot提出的准静态方程描述土体，模型忽略孔隙流体和土颗粒的惯性加速项，同时不考虑孔隙流体对土颗粒的相对变形[23]。

基于准静态方程，将海床考虑为各向同性，各方向上渗透系数相同。孔隙流体的质量守恒方程可以表示为：

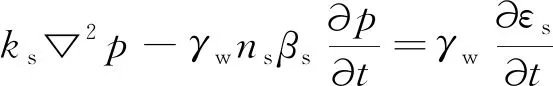
(9)

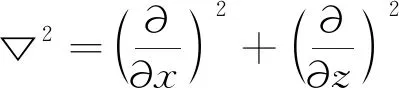
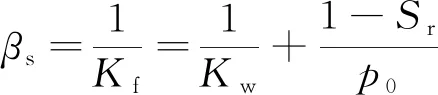
(10)

其中，Kf表示孔隙流体的实测体积模量；Kw为水的真体积模量；p0为绝对静水压力，在模型中取为p0=γwd，d是水深；Sr为土体饱和度。

孔隙水压的控制方程可表述为：

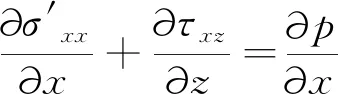
(11)

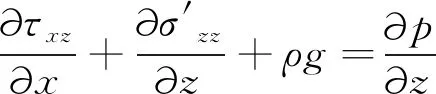
(12)

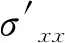
式(11)和(12)中的有效应力可以从多孔弹性理论得出：

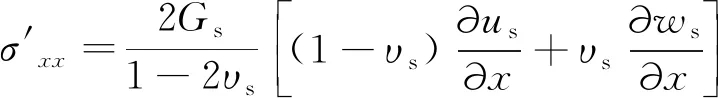
(13)

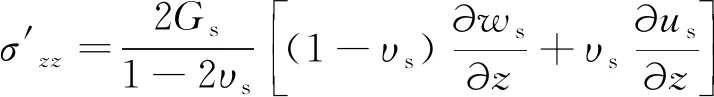
(14)

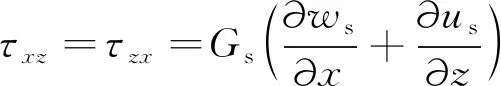
(15)

其中，Gs表示土体剪切模量，通过杨氏模量Es和泊松比υs可以表示为Gs=Es/[2(1+υs)]。

1.3 边界条件

数值模型通过波流模块模拟波浪场，随着波浪的传播，波压力传递到有限厚度的多孔介质海床上，有限厚度的海床底部视为刚性不可渗透。静止水面在z=d+h的位置，波浪传播沿着x轴正方向，竖向z轴以海床底部开始向上为正(如图1)。波浪场中波高为H，波长为L，静止水面距离海床表面的距离为d，有限海床的厚度为h。通过式(11)～(15)可以求解出海床土体中瞬态孔压和土体的变形情况。控制方程式的求解需要结合相应的边界条件，包含海床各界面处边界条件、自由水面的边界条件。

在海床表面，垂直有效应力和剪应力变为0，孔隙水压力等同于海床表面处波浪压力。

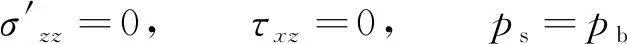
(16)

其中，pb为波浪场在海床表面的波浪压力，ps为孔隙水压力。

海床底部视为不可渗透基岩，海床底部没有位移和垂向渗流，表示为：

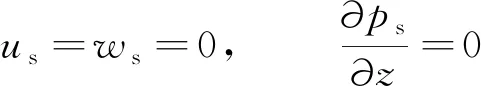
(17)

海床两侧边界视为不可渗透边界，同时没有水平向位移，表示为：

(18)

在波浪自由表面，由于两相流模型中的压力连续条件，波浪自由表面的压力等于大气压。

1.4 模型耦合

模型耦合流程首先要模拟海床基槽周围的流场与压力场，再将压力作为边界条件施加于海床之上以实现海床的孔压和位移计算。最后，将两部分子模块在模型中实现物理场耦合，从而在单位时间步长内实现波流场压力下的土体响应单向耦合计算。

模型的网格主要分为固定网格和移动网格两种，在波流场自动剖分为三角形网格，同时在空气和波浪表面附近采用自动细分方法实现网格较好地与物理场匹配。在开挖基槽部分进行网格细化，以实现更为细致地对此部分流场计算，使计算结果更可靠。移动网格则被用于捕捉自由水面和空气的接触面，自由变形的移动网格采用拉格朗日平滑类型。

1.5 模型验证

首先，将模型计算结果与前人的试验值或解析解进行比较。主要的验证内容分为两部分，波流场验证和海床动态响应验证。为了验证造出波浪的准确性，保证海床受到稳定波浪荷载，将波浪部分的自由波面形态和相应计算区域特征点处水质点运动与解析公式解进行对比。波浪采用Liu 等[25]研究中的波浪参数，波浪参数为波高H=0.143 m，周期T=1.75 s，水深d=0.533 m。选取了造波源区之外1 m位置处的波面振动情况与解析解进行对比，如图2所示，模型计算结果基本上和解析结果相吻合。同时在波浪部分提取波浪自由表面形态与解析解对比验证，结果如图3所示。模型计算结果与解析公式结果基本趋于一致，仅有起始位置处存在少许相位偏差，可能是造波初始阶段未达到稳定导致。整体而言，波浪部分的数值波浪结果和预期解析公式保持一致。

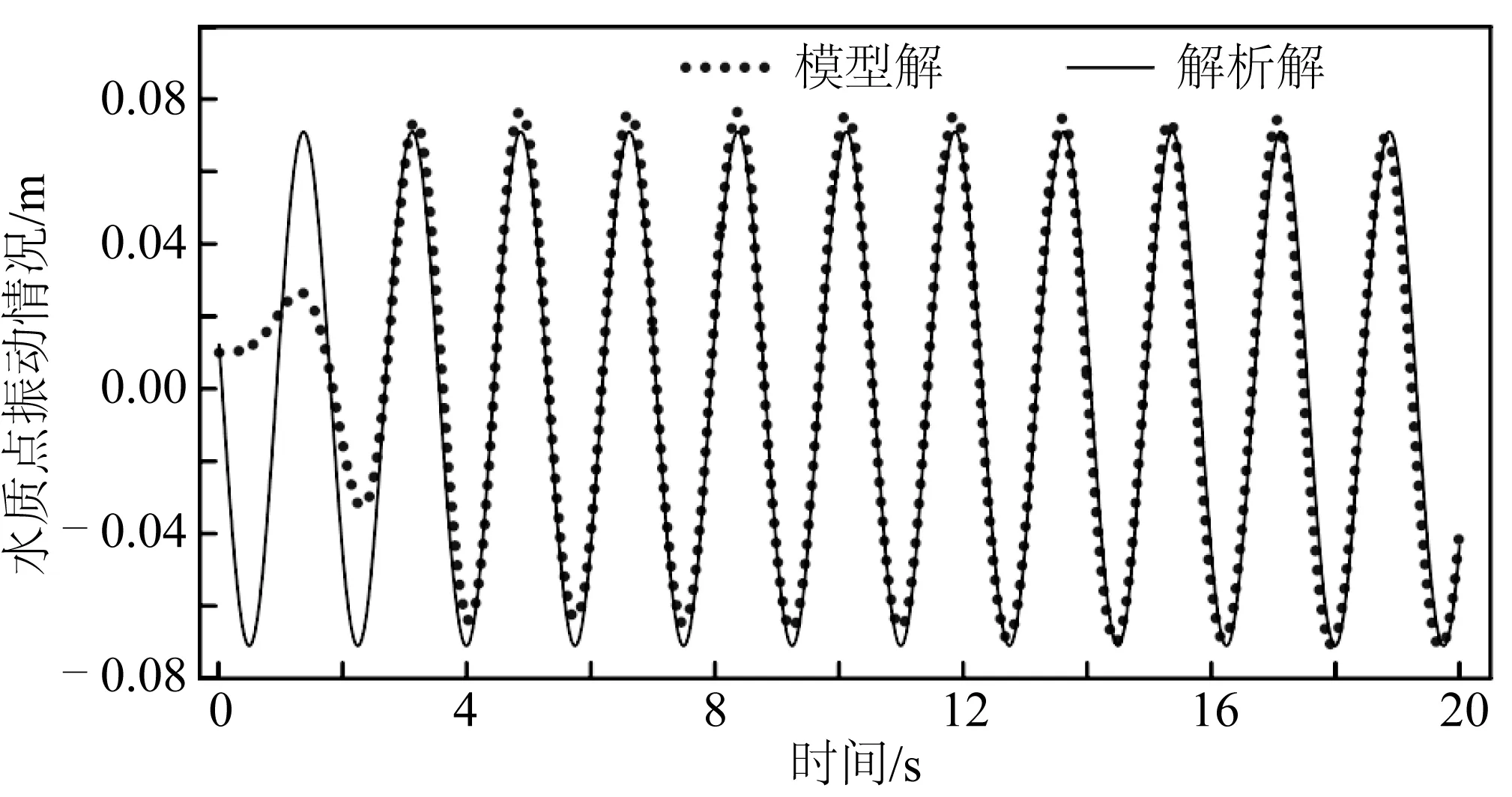
图2 特征点处波面振动情况验证Fig. 2 Validation of the free wave surface vibration at characteristic point

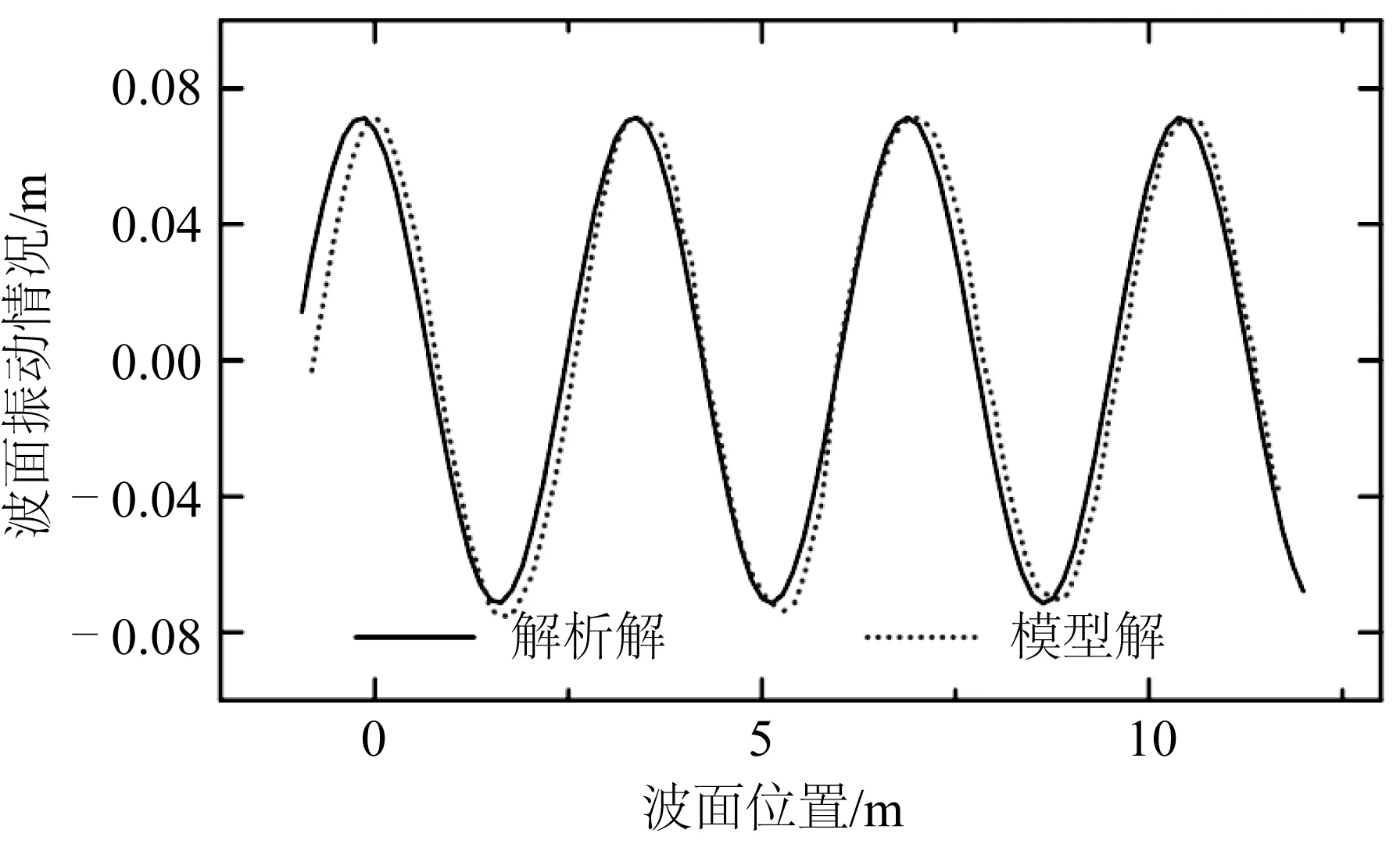
图3 波浪自由表面验证Fig. 3 Validation of the free wave surface

为了验证波流相互作用下波面水质点振动情况，将模型与Chen等[26]试验结果进行对比，模拟波流同向(U=0.2 m/s)和波流反向(U=-0.2 m/s)的特征水质点处波面振动情况。Chen等[26]所采用波浪参数为：波高H=0.05 m，水深d=0.6 m，波周期T=1 s。将模型结果与Chen等[26]试验中G3波浪仪测量数据对比，结果如图4所示，结果显示模型可以有效反映波流共同作用下的波浪特征。

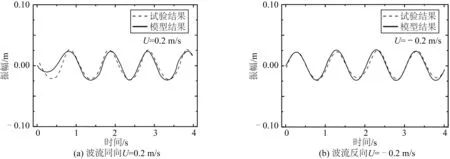
图4 波流相互作用下波面验证Fig. 4 Wave surface validation under wave-current interaction

在海床土体动态响应验证部分，将模型结果与Qi和Gao[27]试验数据进行对比，试验的主要参数为：波高H=0.102 m，波周期T=1.2 s，流速U=0.23 m/s；土体渗透系数K=1.88×10-4m/s，海床相对密实度Dr=0.352，土体浮重度γ′=9.03 kN/m3。试验中装土的特制土箱固定在水槽中段，采用孔压计测量土体表面和下部孔压的变化，具体试验布置可在Qi和Gao[27]研究中得到。模型结果与试验中的孔压计PPT1和PPT2对比，结果如图5所示，展示了两个波浪周期内的土层表面和表面之下的孔压变化。数值结果与试验数据具有良好一致性，即模型对波流压力下的海床孔压模拟具有良好应用性。

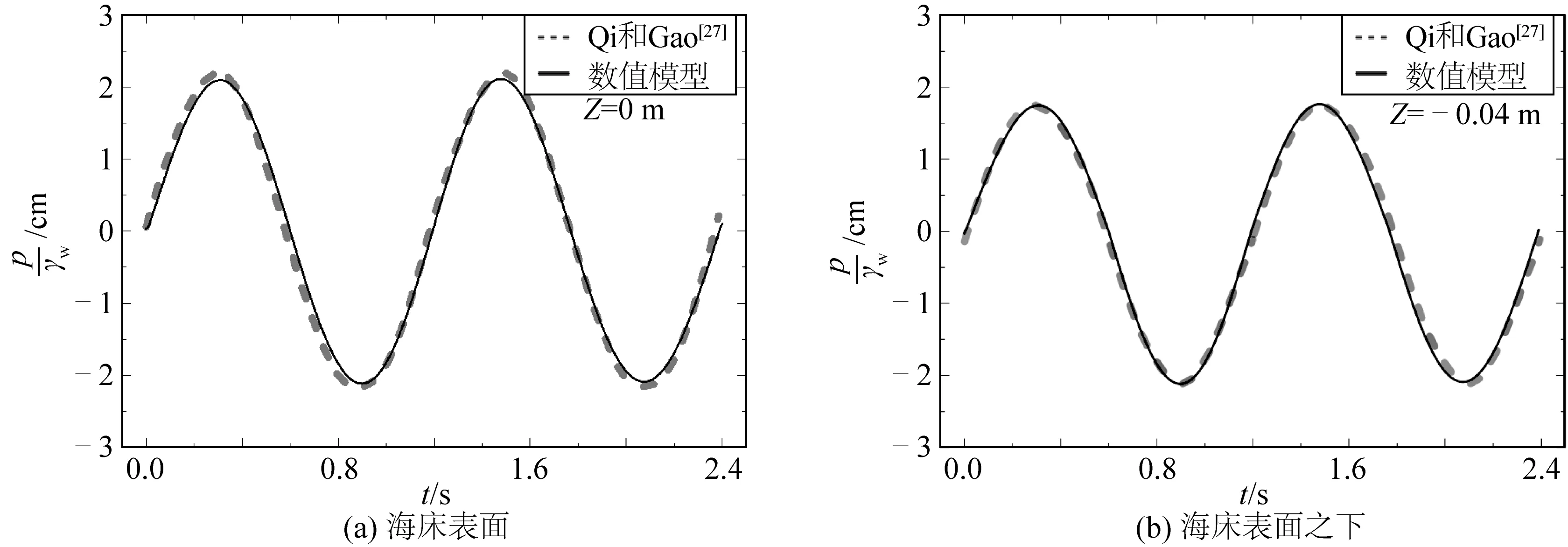
图5 数值模型与Qi和Gao试验数据对比结果Fig. 5 Comparison between numerical and experimental data of Qi and Gao

2 数值模型应用

2.1 海床初始固结

在工程活动如水下基槽开挖影响下，海床土体会进入新的固结状态。孔隙水压力消散，有效应力增加，基础会产生一定沉降[28]。首先确定受扰动之后海床的初始固结状态和有效应力分布情况。文中选用的波浪、土体参数和边坡参数见表1。波浪和土体参数参考渤海区域极端情况下记录的参数[29]，计算沉管隧道开挖形成的基槽在波流共同作用下的动态响应。后文无特别说明情况下均采用表中参数。基槽开挖后的有效应力分布情况如图6所示，作为初始有效应力应用在后续分析中。

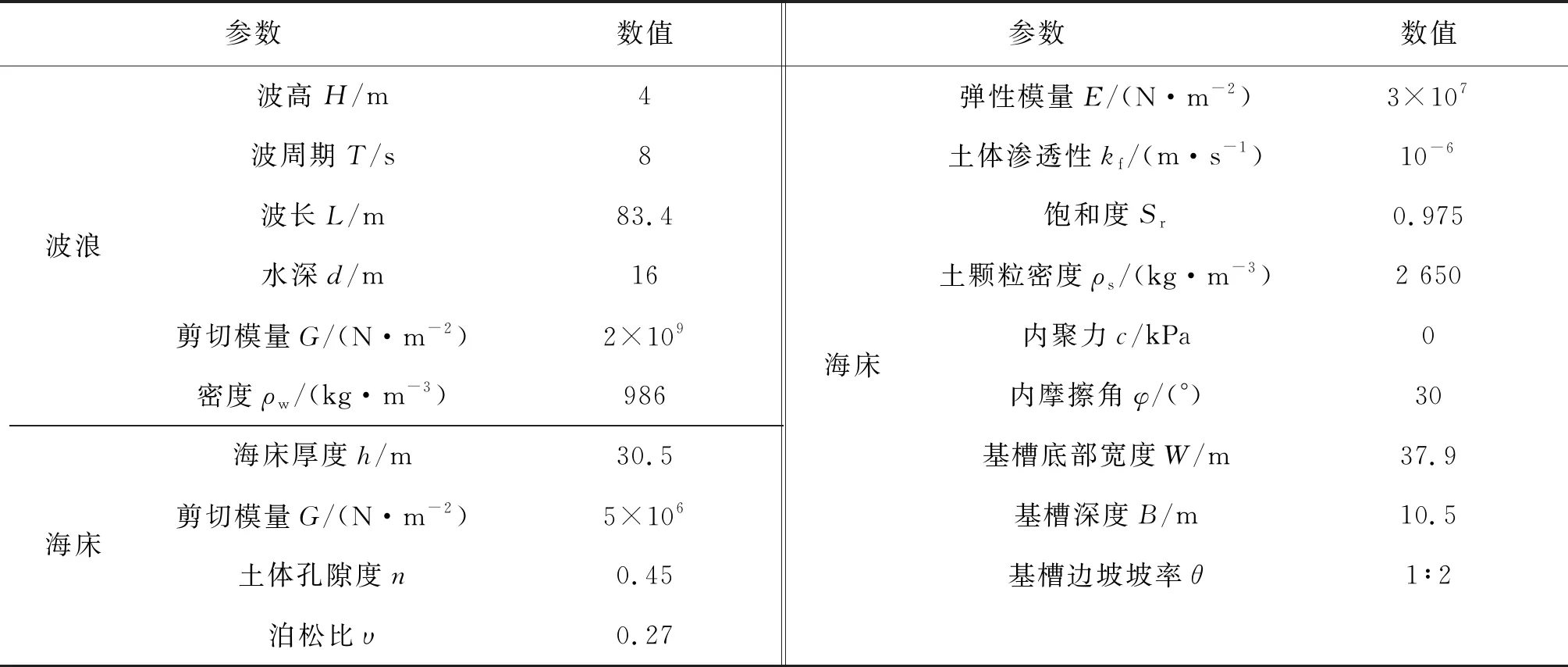
表1 研究中的参数取值Tab. 1 Parameters in this analysis

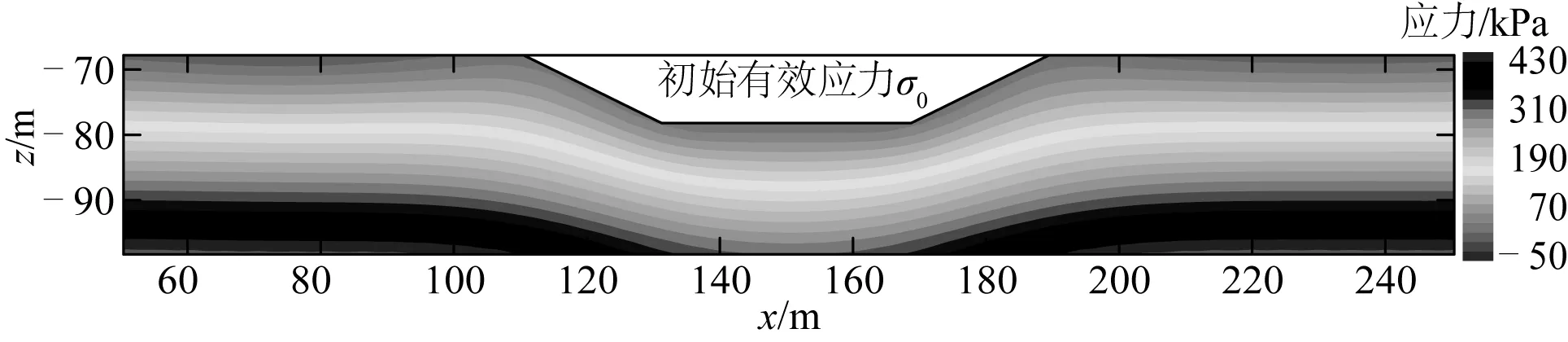
图6 基槽开挖完成后的初始有效应力分布Fig. 6 Initial effective stress distribution after trench excavation

2.2 瞬态液化

波浪作用下的海床液化对于近海工程结构物的设计施工影响重大。目前已有多种波浪作用下的海床液化判别依据[30-32]，文中采用Zen和Yamazaki[30]提出的二维液化判别准则：

(19)

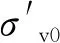
图7给出了计算沉管隧道基槽开挖之后海床土体液化深度为最大值的情况，上半部分为波浪作用于海床表面的动压力，下半部分深色区域展示液化区域。模型采用了表1的参数，计算结果和前人得出的结论保持一致，瞬态液化主要发生在海床表层区域，由于孔压产生的相位滞后性而周期性出现在波谷之下[33-34]。液化区域分布和最大液化深度的计算对海底人工基槽设计和施工具有一定指导意义。

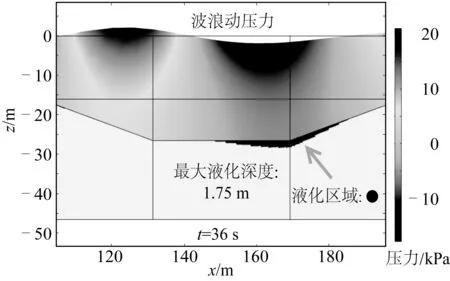
图7 基槽开挖完成后海床土体液化情况Fig. 7 Seabed soil liquefaction after trench excavation

2.3 波浪参数的影响

对波浪参数对海床的液化情况和孔隙水压力分布影响进行参数分析。分别取不同波浪高度H=3 m，4 m，5 m，采用造波模型产生相应的波浪计算基槽周围土体的最大液化深度，结果如图8(a)所示，随着波高的增大，基槽部分的最大液化深度分别为0.98 m，1.30 m，1.63 m。取不同的波浪周期T= 6 s，7 s，8 s，分析波浪周期对最大液化深度的影响。从图8(b)可以看出，最大液化深度随着波浪周期的增大呈指数形式增大，海床最大液化深度分别为1.35 m，1.52 m，2.10 m。即长周期的波浪对海床土体液化破坏显著增大。

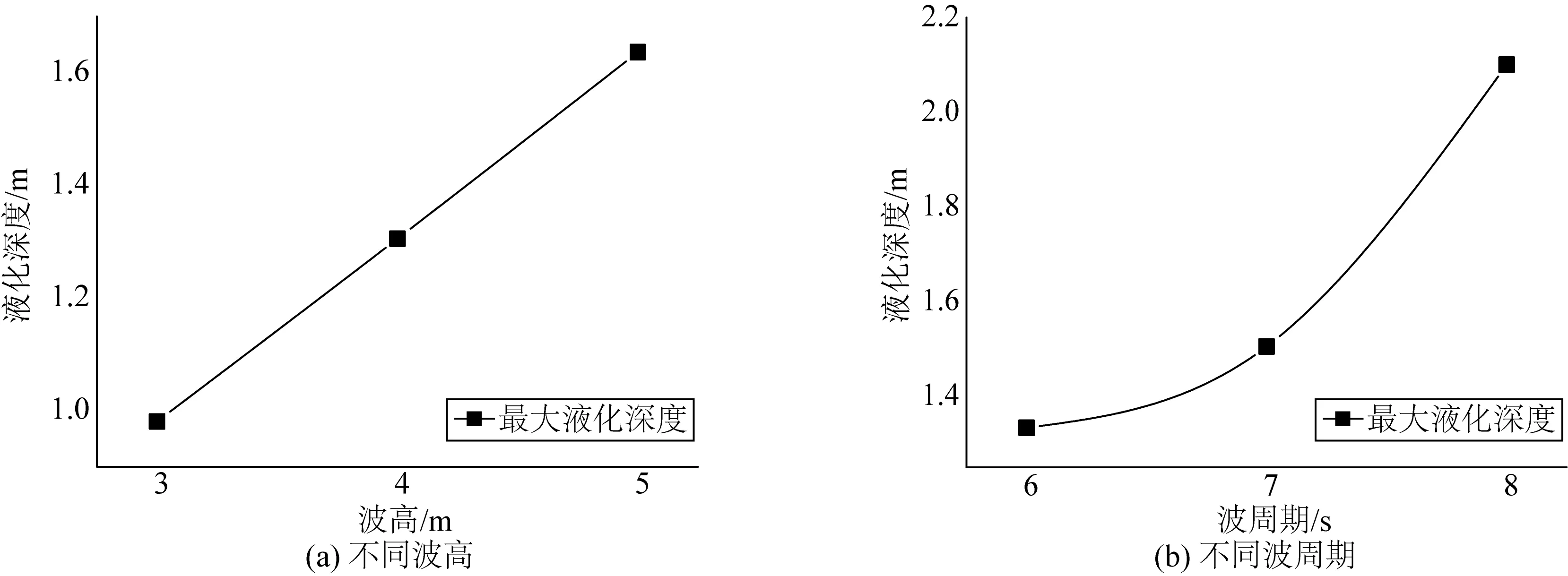
图8 不同波高和波周期条件下海床土体最大液化深度变化Fig. 8 Variation of maximum liquefaction depth of seabed soil under different wave heights and wave periods

同时，计算得出基槽内最大孔隙水压力随不同波高和不同波周期的垂向分布情况。结果如图9(a)所示，最大孔压|ps|max/0.5γwH随着波高的增大而增大。但3种不同波高情况下当z/hs=-1时(即海床底部)，孔隙水压力趋近于0。如图9(b)所示，随着波浪周期的增大，最大孔压也相应增大。这些规律和图8中液化深度分析呈现的规律相一致，正是因为海床中的超孔隙水压力增大超过海床自身的初始有效自重，导致了液化的发生。

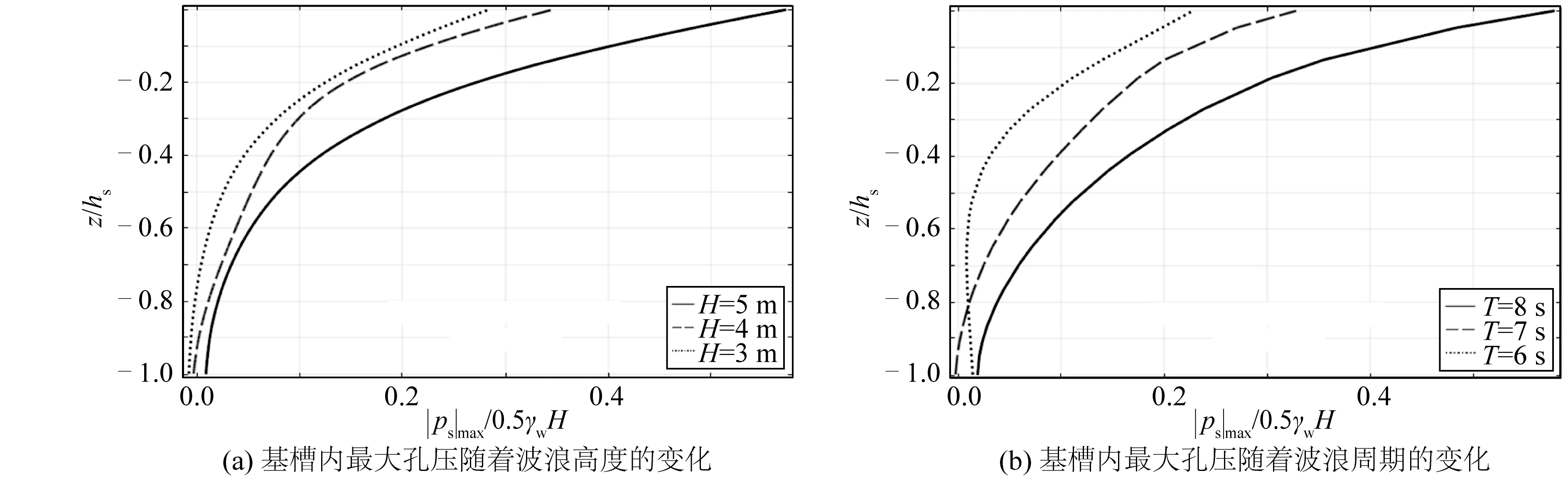
图9 海床土体的孔压分布随着波浪高度和周期的变化Fig. 9 Pore pressure distribution of seabed soil varies with wave height and period

2.4 海流参数的影响

如前所述，波流共同作用下的波浪形态和仅存在波浪时有很大不同。针对不同流速(范围-2～2 m/s，以0.5 m/s为间隔)对波浪形态影响进行参数分析，旨在得到波-流共同作用对波浪主要特征参数的影响。结果如图10所示，对计算得到的波高和波长采用无量纲化处理，即同输入波高H和波长L(见表1)的比值。波浪在同向海流作用下波长增大波高减小，波陡度减小。相反，在反向海流的作用下，波长变短而波高增大，波陡度增大。

图10 波浪在不同流速下的波高和波长变化Fig. 10 Change of wave height and wave length with different current velocities

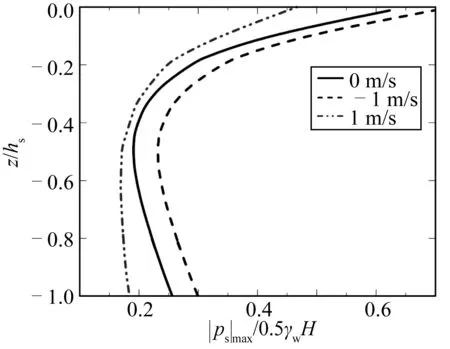
图11 不同流速波流共同作用下海床最大孔压分布情况Fig. 11 Distribution of maximum pore pressure in the seabed with different current velocities

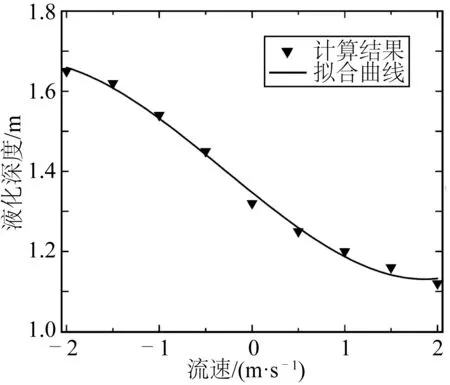
图12 不同流速下最大液化深度 Fig. 12 Maximum liquefied depth with different current velocities

海流对海床动态响应和破坏情况影响重大，在实际海洋环境中，波浪和海流(潮流)常常同时存在。在不同的波流组合方式作用下，海床中的孔压和有效应力分布会产生显著变化。分析不同海流流速与波浪的公共作用对海床中孔压分布的影响，对海床受波流共同作用影响的分析有重要意义。选取三种不同的海流速度，-1 m/s，0 m/s，1 m/s，分别计算波流反向作用、仅波浪作用和波流同向作用下的海床动态响应结果。如图11所示，海床不同深度处的最大孔压在波流反向的情况下达到最大，而在波流同向的情况下最小。

在上述分析的基础上，模型计算了海床最大液化深度在相同波浪参数(见表1)伴随不同流速下的变化，流速变化范围为-2～2 m/s，以0.5 m/s为间隔。结果如图12所示，在反向海流作用下，海床的最大液化深度同比有所增大。而在同向海流作用下，海床的最大液化深度相应减小。值得注意的是，反向海流对液化深度的影响(1.65 m相对于1.32 m，同比增大25%)比同向海流的影响(1.12 m相对于1.32 m，同比减小15%)更大。图12中基于线性回归分析给出了不同流速下最大液化深度ZL的拟合曲线为：

ZL=0.013 6u03+0.012 1u02-0.186 1u0+1.347 5

(20)

式中：u0为流速，拟合曲线的相关参数R2=0.990 9。

3 结 语

研究波流荷载下开挖基槽周围海床的动态响应，提出基于RANS方程和Biot固结“Q-S”理论的波浪-海床耦合计算数值模型。将模型详细地与前人试验解和解析解对比验证后，应用于计算波流共同作用下的波浪形态变化，以及基槽海床动态响应计算，包括孔压分布和液化深度变化。基于数值计算结果，结论可以总结如下：

1) 基槽开挖之后的初始应力场和应变场会有很大改变，后续动态响应分析应当以开挖后新的固结状态作为初始状态考虑。

2) 开挖之后基槽内土体的最大孔压|ps|max/0.5γwH和液化深度ZL随着波浪周期T和波高H的增大而增大。

3) 波浪在同向海流作用下波长增大，波高减小，波陡度减小；在反向海流作用下波长减小，波高增大，波陡度增大。同样条件下，反向海流对波浪形态的影响更大。

4) 反向海流作用下，海床内的最大孔压和液化深度都相应增大。同时，反向海流对最大液化深度的影响更大。基于具体波浪参数提出的流速与最大液化深度关系对相应研究和工程应用具有参考价值。