基于能量平衡的跨海桥梁钢管桩局部冲深计算
郭 健,汪 涛,王金权,吴继熠
(1. 浙江工业大学 桥梁工程研究所,浙江 杭州 310032; 2. 宁波市杭州湾大桥发展有限公司,浙江 宁波 315000)
桥墩处于复杂水流环境中,桥墩的阻水效应产生的水流冲击及涡流作用,会引起桥墩周围的剧烈淘沙运动,在墩周形成局部冲刷坑,在桥梁基础结构-海水波流-软覆盖层三者之间形成动力耦合效应[1],严重降低桥墩的承载力及稳定性,甚至造成桥梁倒塌。大跨度海域桥梁受随时空变化的潮汐影响[2],桥墩局部冲刷更为严重。据美国联邦公路署统计,72%的桥毁事故是冲刷造成的[3]。现有局部冲刷预测公式在计算跨海桥梁钢管桩局部冲深时存在不确定性,高估桥墩局部冲刷深度,会增大桥墩加固防护费用,特别是大跨度跨海桥梁,而低估桥墩局部冲刷深度,会给实际工程设计带来安全隐患[4]。减少跨海桥梁钢管桩局部冲刷深度预测公式的不确定性可以在不牺牲安全的前提下降低建设成本,同时减少安全隐患。
近几十年来,众多学者在预测桥墩局部冲刷深度方面做了大量研究。Roulund等[5]、Melville等[6]、Richardson等[7]、Zhao等[8]、马丽丽等[9]基于数值模拟及室内试验结果,认为局部冲刷最大值出现在墩前,这一观点得到国内外学者普遍认可。Melville等[10]、Laursen等[11]、Chiew等[12]、Pol等[13]通过大量试验结果,筛选出影响局部冲刷深度的主要因素,提出了桥墩局部冲刷深度预测公式。我国公路和铁路部门在泥沙起动理论的基础上,制定了65-1式。美国联邦公路署(FHWA)[14]推荐使用HEC-18方程,Timothy等[15]在保持HEC-18方程结构形式的基础上,建立了适用于非黏性土条件下的优化方程。Bateni等[16]、Lee等[17]利用神经网络的方法,以现场观测数据为样本进行训练和测试,建立桥墩局部冲刷神经网络模型,以此预测冲深。前苏联的雅罗斯拉夫切夫首先基于能量平衡理论,推导得出桥墩冲刷深度公式。然而由于海域水动力特性的复杂,上述公式对于跨海桥梁钢管桩局部冲深的预测效果并不理想。
在上述研究基础上,考虑墩前冲刷坑内泥沙搬运过程中的能量平衡,以及冲刷过程中冲刷坑本身深度及范围变化对冲刷产生的影响,并根据量纲平衡原则建立二元线性回归模型,采用最小二乘法通过大量数据进行线性拟合,推导出概念清晰、精度较高的跨海桥梁钢管桩局部冲刷深度预测公式。
1 桥墩局部冲刷机理
桥墩周围存在着十分复杂的水流结构,包括桩前壅水、下降水流、墩底马蹄形漩涡、墩侧绕流漩涡、墩后尾流漩涡以及床面附近形成的小漩涡(如图1所示)。
桥墩的阻水作用引起复杂的三维流态,可将墩前水流分为三层[18],墩前水面薄层撞击桥墩形成壅高,中层水流在墩前流速为零,产生向下的压力梯度迫使底层水流形成向下射流冲刷床面。向下射流受到河床阻碍同时受中层水流影响,形成向墩前外侧翻滚的马蹄形漩涡,这些中心负压的马蹄形漩涡不断作淘沙运动,将泥沙搬离冲刷坑。Unger等[19]、Guan等[20]的试验结果表明,向下射流及其转化成的马蹄形漩涡是墩前冲刷坑发展的主要原因。
随着局部冲刷的进行,冲刷坑不断发育变大,坑内水流流速降低,泥沙粗化,坑内泥沙抗冲能力增强,直至与水流冲刷作用平衡,此时局部冲刷达到冲淤平衡状态,冲刷坑的深度及宽度不再增加。Unger等[19]、Sheppard等[21]、Dey等[22]的试验结果表明,达到冲淤平衡状态时的墩前冲刷坑可视为一个坡度等于泥沙休止角的半圆锥体,且局部冲刷的最大值点出现在墩前。
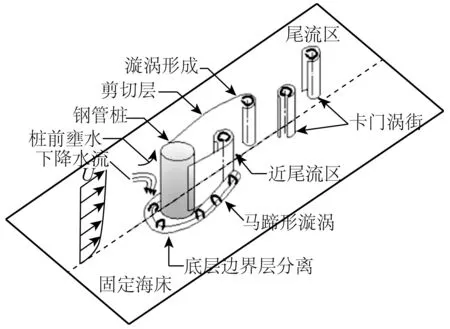
图1 圆柱形桥墩周围的水流结构Fig. 1 Flow structure around cylindrical piers
2 已有预测公式的影响因素
我国规范JTGC30-2002《公路工程水文勘测设计规范》[23]推荐采用1964年桥渡冲刷学术会议提供的桥墩局部冲刷65-1修正式和65-2修正式。
桥墩局部冲刷65-1修正式表示为:
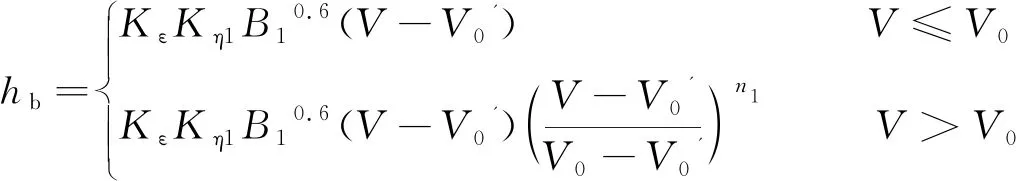
(1)
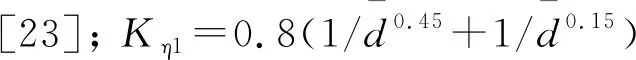
桥墩局部冲刷65-2修正式表示为:
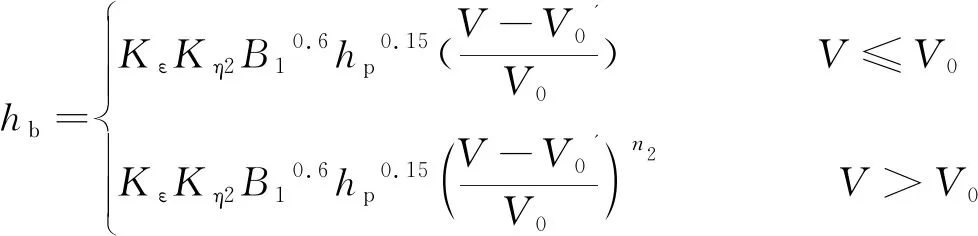
(2)
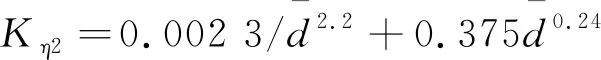
美国联邦公路署(FHWA)[14]推荐使用HEC-18方程预测桥墩局部冲刷深度。HEC-18方程表示为:
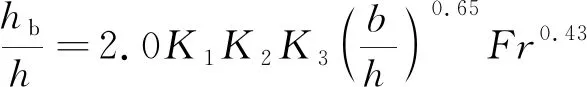
(3)
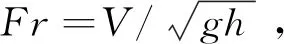
韩海骞等[24]利用水槽试验以及河口海湾地区的相关研究成果,提出了适用于潮流条件下的局部冲刷深度计算公式。韩海骞公式表示为:
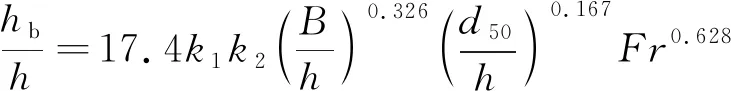
(4)
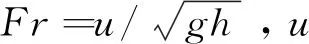
综合以上四式及国内外众多局部冲深计算公式及研究结果,对于跨海桥梁钢管桩,局部冲刷深度的主要影响因素包括三个方面:水流动力特征(水流行进流速V,重力加速度g,行进水深H,弗劳德数Fr);桥墩特征(桥墩宽度b);床沙特征(泥沙粒径d,密度ρs)。故关于跨海桥梁钢管桩局部冲刷深度hb的函数式可表示为:
hb=f(V,g,H,Fr,b,d,ρs)
(5)
3 局部冲刷深度预测公式
为了得到局部冲刷坑的整体分布形态,采用Flow-3d软件建立三维数值模型。根据浙江省河海测绘院对杭州湾跨海大桥桩基局部冲刷的观测资料,选取近年来冲刷增幅显著的匝道桥区域ZD18号桩,建立三维数值模型。
Flow-3d自带的冲刷模块采用基于Mastbergen和Berg[25]研究的经验输沙模型。泥沙运动方程包括推移质输沙率方程和悬移质输沙方程。
推移质输沙率方程:
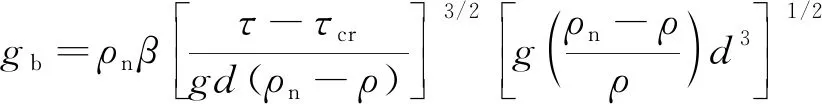
(6)
悬移质输沙方程:
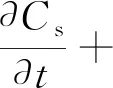
(7)
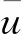
湍流模型选取LES模型模拟三维水流的流动,采用嵌套网格对墩周局部加密,网格总数为1 368 640,形状为均匀六面体,模拟时间步长为0.001 s,模拟时间为1 800 s。其余模型具体参数设置见表1,边界条件设置见图2。

表1 模型参数设置Tab. 1 Parameters setting of model
局部冲刷坑整体形态分布见图3,与Melville[26]试验所得结果大致吻合,冲刷坑纵向及侧向坡度约等于泥沙休止角(30°),局部冲刷最大值点出现在墩前。
基于能量平衡理论,推导局部冲刷深度预测公式。由于墩前向下射流及马蹄形漩涡是墩前冲刷坑形成的主要原因,故可认为,墩前水体的动能等于搬运墩前泥沙所需的能量。由于实际冲刷情况较为复杂,作出了以下简化与假定[27],排除不必要因素的干扰:
1) 桥墩局部冲刷是在一般冲刷完成的基础上进行的,以下公式中的水深及流速均是一般冲刷完成后的水深及流速。
2) 局部冲刷完成后的墩前冲刷坑形态为一个高为hb,上底半径为R,下底半径为r的半圆台体。
3) 将被冲走的泥沙看成整体,其质心位于距圆台形冲刷坑上表面1/3hb处。
4) 圆台形冲刷坑侧壁坡度等于泥沙的水下休止角φ。
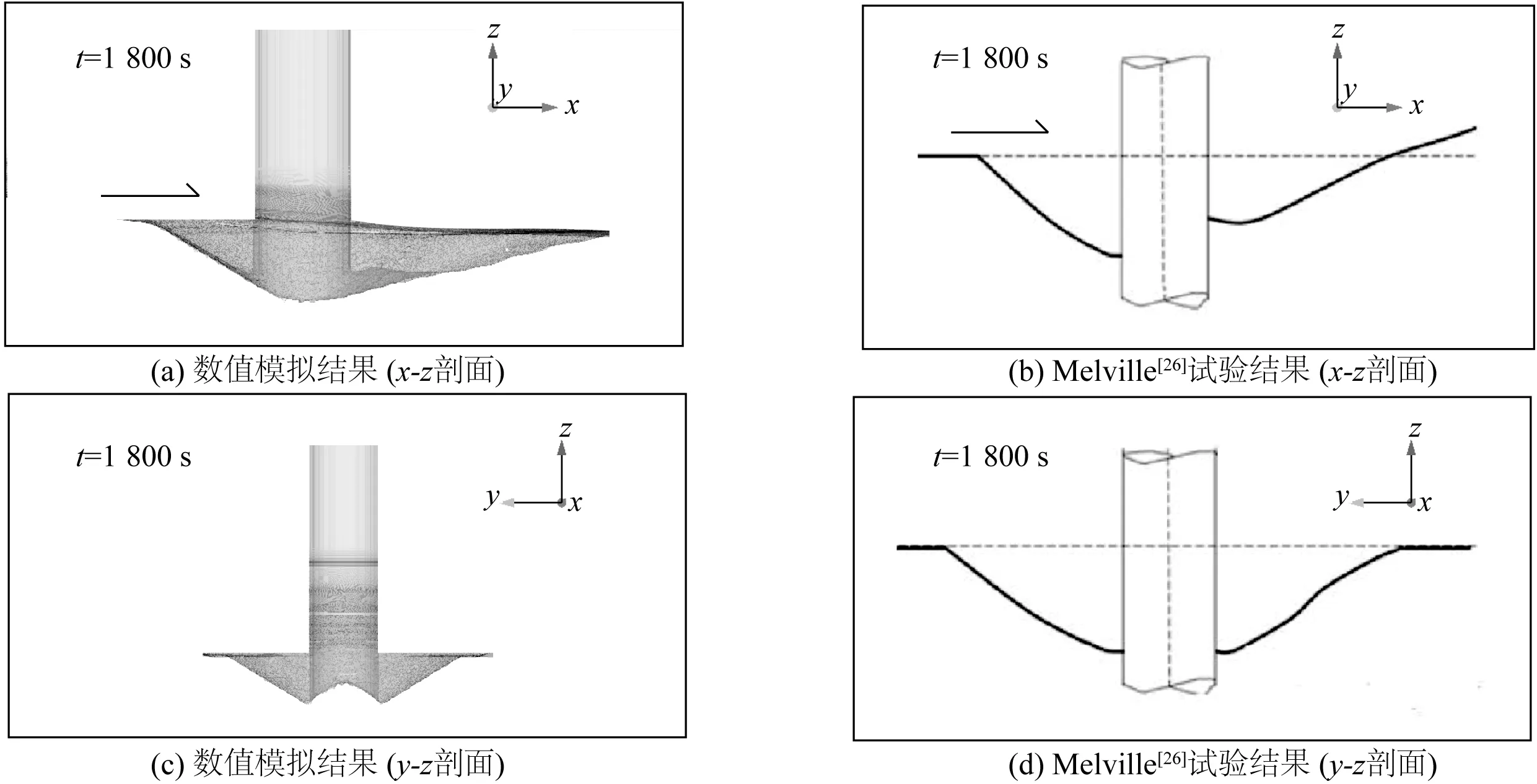
图3 冲刷坑形态对比Fig. 3 Comparison of the shapes of local scour holes
基于以上简化及假设,冲刷坑深度计算图如图4所示。
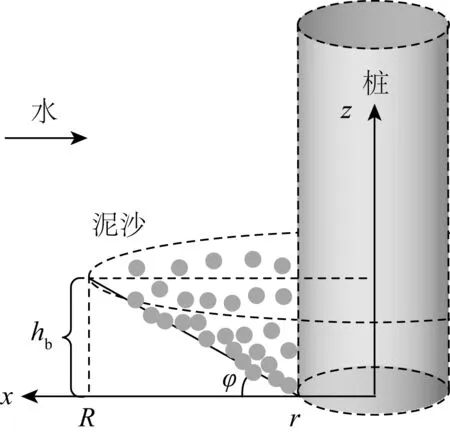
图4 局部冲刷坑计算图Fig. 4 Local scour calculation figure
墩前被冲走的泥沙体积等于:
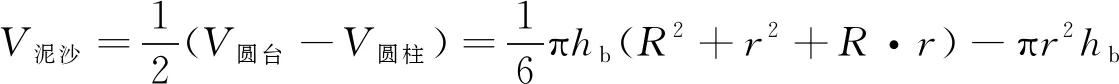
(8)
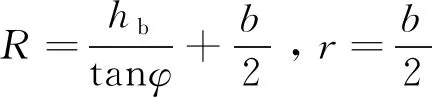
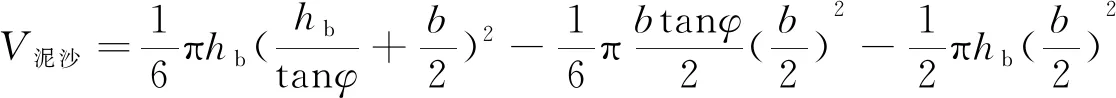
(9)
简化后得:
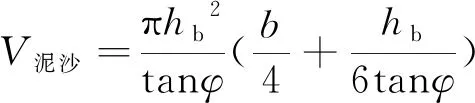
(10)
根据张红武等[28]提出的天然沙水下休止角公式对泥沙粒径及水下休止角的关系进行描述,可表示为:
φ=32.5+1.27d
(11)
其中,d为泥沙中值粒径,mm。
则搬运墩前冲刷坑内泥沙所作的功W可表示为:
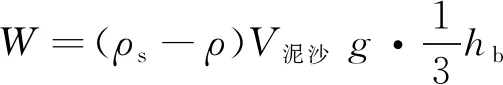
(12)
其中,ρs为泥沙密度,ρ为水密度,g为重力加速度。
墩前水体(下降水流、马蹄形漩涡)搬运墩前泥沙的有效动能E可表示为[29]:
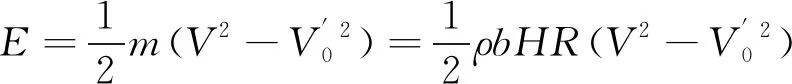
(13)
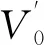
基于能量平衡理论,搬运墩前冲刷坑内泥沙所作的功W等于墩前水体的有效动能E,故可得:
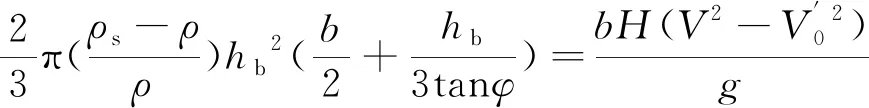
(14)
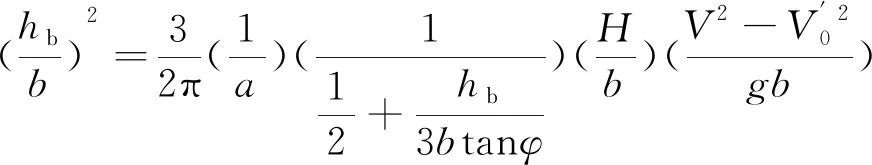
(15)
即:
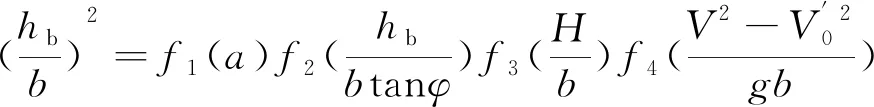
(16)
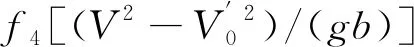
由于在上式推导过程中做出了一定假设,且实际冲刷情况十分复杂,存在许多不可判断的参数影响,故通过冲刷试验数据及现场观测数据对公式的系数及指数进行调整修正。将式(15)中3/(2πa)表示为K,并根据量纲平衡改写成:
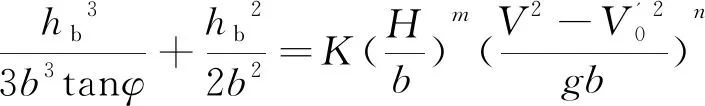
(17)
将上式两边同时取对数得到多元线性方程:
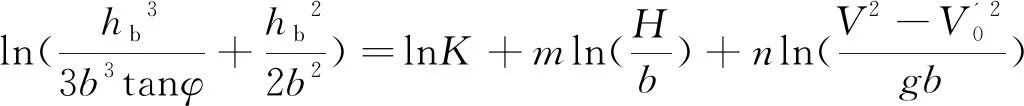
(18)
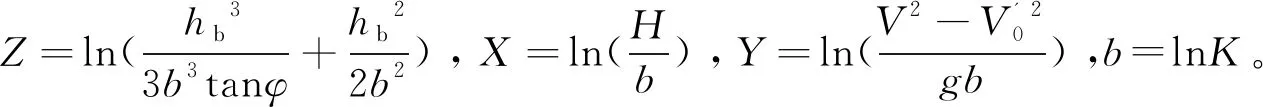
选取试验及现场观测数据总计55组对上式进行拟合,这些数据包括环杭州湾区域的三座跨海大桥的试验数据及现场观测数据[30-32],见图5,三座跨海大桥均邻近杭州湾海域,潮差大、涨落潮流速急,地质条件为淤泥质海床,其中嘉绍大桥水深8~25 m,行进流速6.05~6.70 m/s,起动流速0.51~0.75 m/s,泥沙类型为细粉土,粒径范围0.02~0.4 mm,中值粒径0.065 mm,桩径0.75~30 m;杭州湾大桥水深10~25 m,行进流速1.42~3.46 m/s,起动流速0.57~0.84 m/s,泥沙类型为细颗粒悬浮泥沙,粒径范围0.004~0.016 mm,中值粒径0.049 mm,桩径5.2~29.2 m;金塘大桥水深4.5~23 m,行进流速1.76~3.33 m/s,起动流速0.74~1.11 m/s,泥沙类型为粉砂,粒径范围0.003 7~0.013 4 mm,中值粒径0.027 mm,桩径0.8~27.4 m,典型桩基础结构形式见文献[31]。
采用最小二乘法,通过Matlab对以上方程进行线性拟合得,m=0.731,n=1,b=2.431。具体拟合参数见表2。具体的数据拟合分布情况见图6。

表2 数据拟合参数及优度分析Tab. 2 Goodness of fit
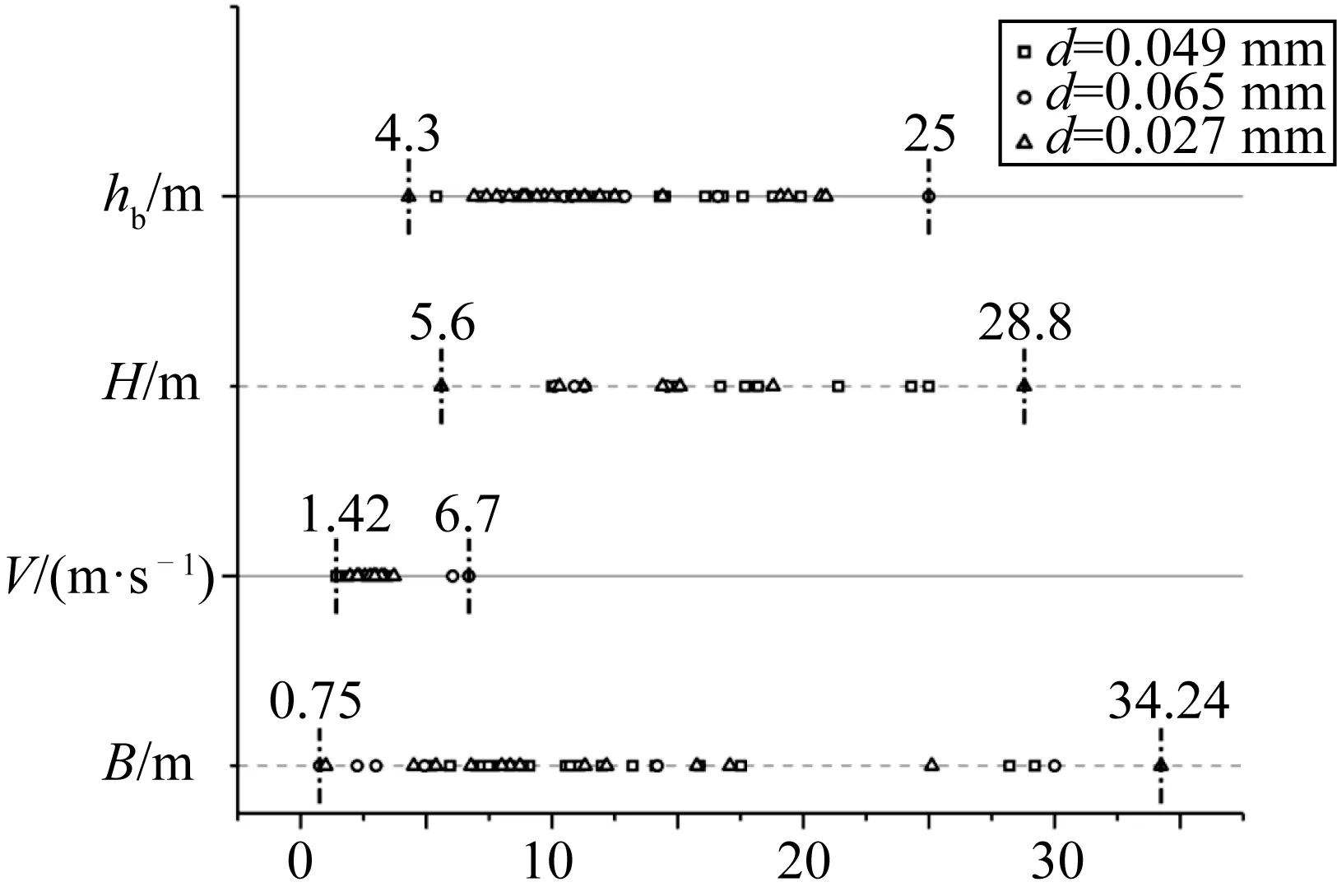
图5 试验及现场观测数据分布Fig. 5 Experimental and on-site test data distribution
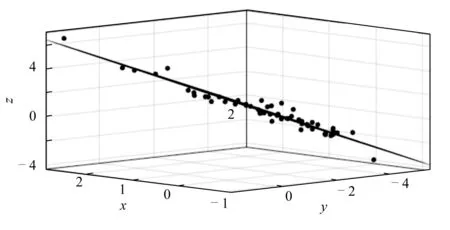
图6 数据拟合Fig. 6 Data fitting
可见线性拟合效果较好,所得局部冲刷深度预测公式为:
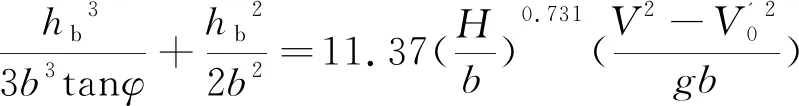
(19)
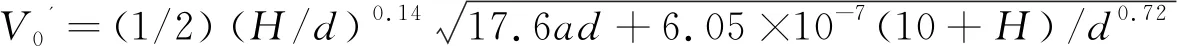
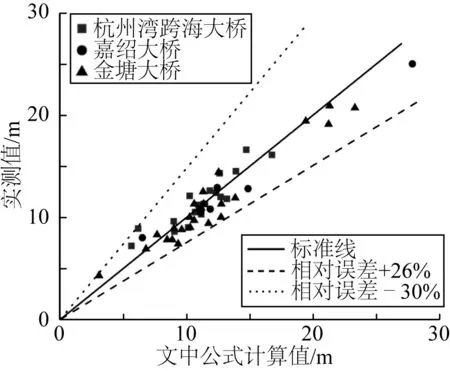
图7 桥梁局部冲刷深度实测值和计算值相关性Fig. 7 Local scours measured values and calculation values
4 公式验证与比较
另行选取36组数据作为验证数据集,分为两组,组1包括Sheppard等[21]、AI-Shukur[33]、Ahmad等[34]、Ettema等[35]搜集的试验及实测资料以及瓯江大桥部分试验及现场实测数据,共计16组,泥沙粒径范围为0.255~0.7 mm;组2包括某强潮海湾跨海大桥[36]、苏通大桥[37]、妈屿跨海大桥[37]、某跨江大桥[38]、杭州湾跨海大桥的试验及运营期间现场观测数据,共计20组,泥沙粒径范围0.008~0.2 mm。分别运用我国规范内65-1修正式及65-2修正式,美国规范内HEC-18方程,以及文中公式对组1内数据进行计算,具体计算过程及结果见表3和图8;由于65-1修正式、65-2修正式、HEC-18方程在淤泥质海床条件下表现出失效性,运用韩海骞公式及文中公式对组2内数据进行计算,具体计算过程及结果见表4和图9。
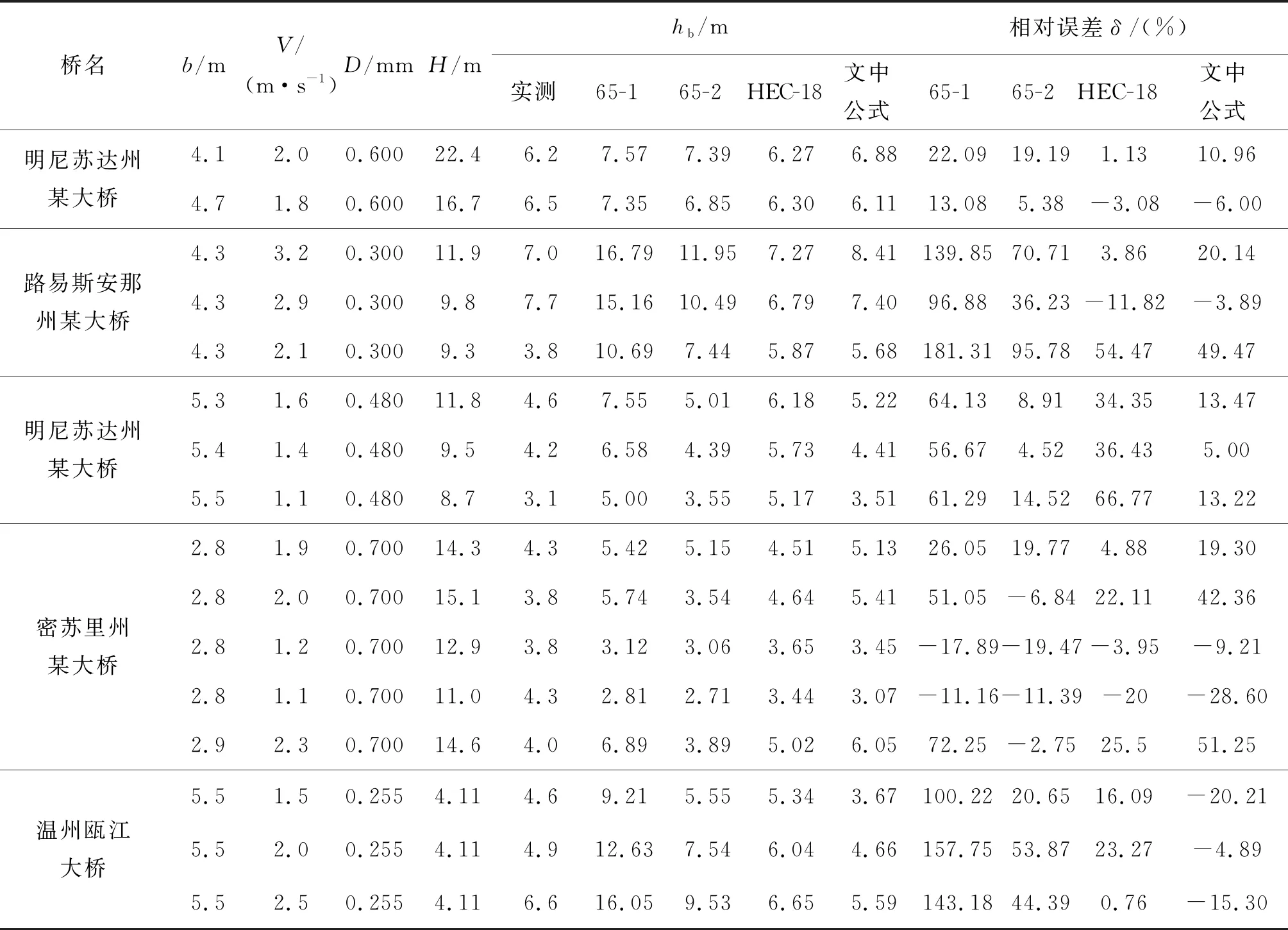
表3 桥梁局部冲刷计算公式误差分析(组1)Tab. 3 Error analysis of local scour depth formula (group 1)
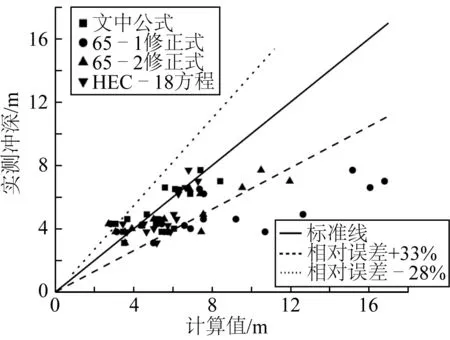
图8 桥梁局部冲刷计算公式误差分析(组1)Fig. 8 Error analysis of local scour depth formula (group 1)
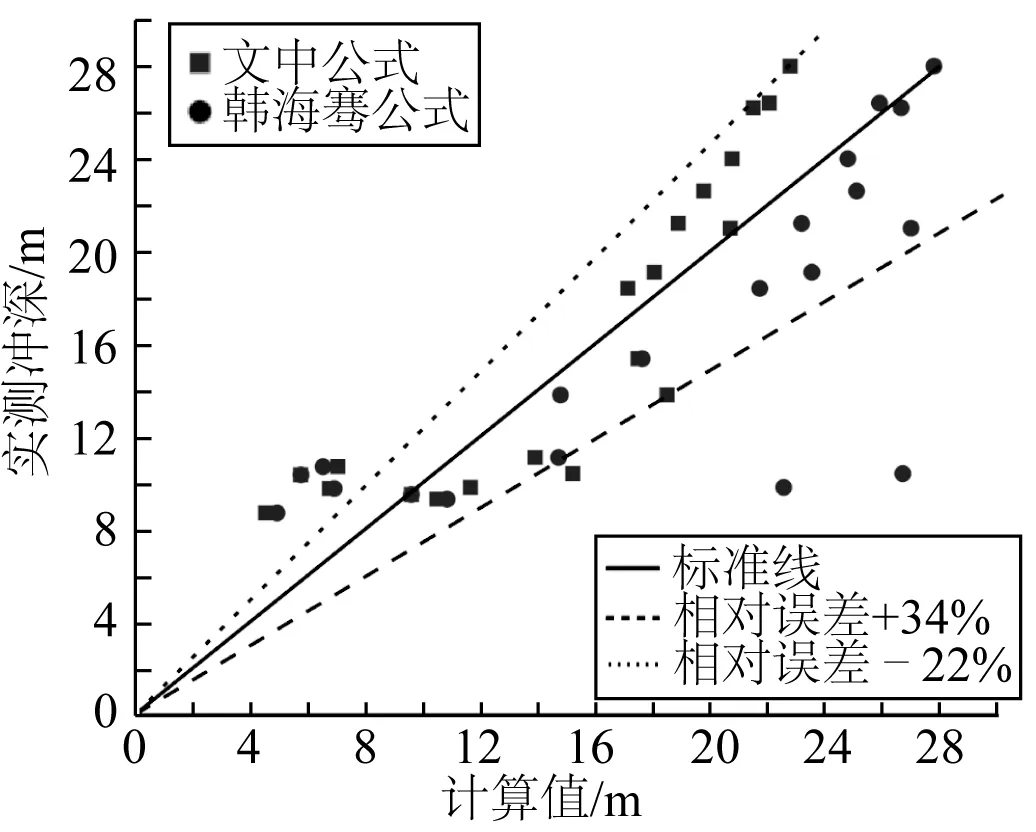
图9 桥梁局部冲刷计算公式误差分析(组2)Fig. 9 Error analysis of local scour depth formula (group 2)
依图8,对于泥沙粒径为0.255~0.7 mm的验证数据集组1,相较于我国规范内65-1修正式及65-2修正式,该公式的精度有明显提高,相对误差控制在-28%~+33%以内。如图9所示,对于泥沙粒径为0.008~0.2 mm的验证数据集组2,该公式在计算苏通大桥、杭州湾跨海大桥、妈屿跨海大桥、某跨江大桥局部冲深时均展现出良好适用性,相对误差控制在-22%~+34%以内,与韩海骞公式相似,计算某强潮海湾跨海大桥局部冲深时,相对误差在-47%~-30%,这可能是该公式未能充分考虑强潮影响所致。以上验证结果表明,该公式的适用范围广,且精度较高。
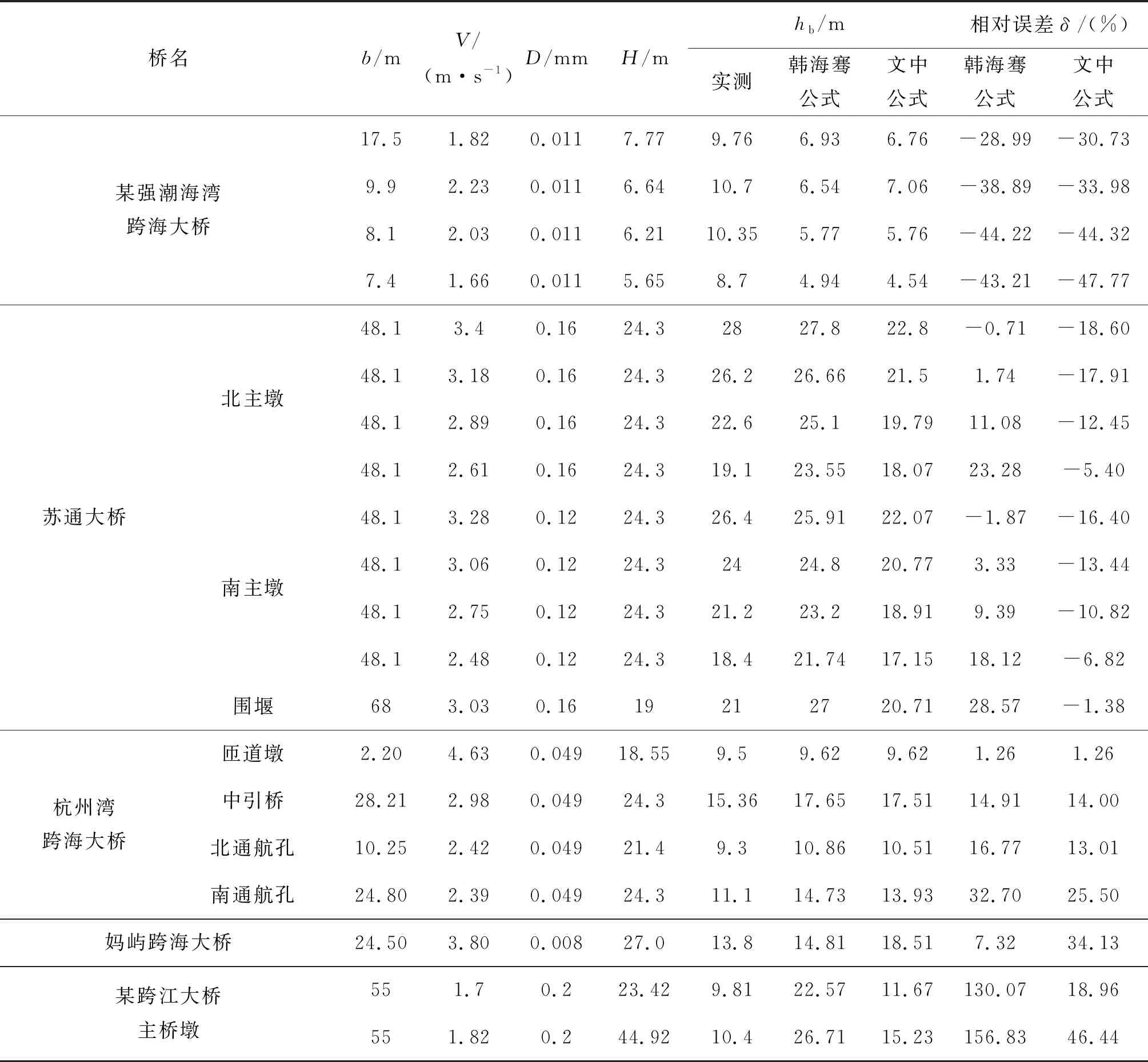
表4 桥梁局部冲刷计算公式误差分析(组2)Tab. 4 Error analysis of local scour depth formula (group 2)
5 结 语
结合前人研究成果分析桥墩局部冲刷机理,认为向下射流及其转化成的马蹄形漩涡是桩前冲刷坑发展的主要原因,并利用Flow-3d建立三维数值模型验证了局部冲刷最大值点出现在桩前,且冲坑坡度近似等于泥沙水下休止角(30°)的结论。
基于以上分析结果,在做出一定合理假设的前提下,考虑墩前冲刷坑内泥沙搬运过程中的能量平衡,建立了概念清晰、精度较高的跨海桥梁钢管桩局部冲刷深度预测公式。公式系数由环杭州湾区域三座跨海大桥的55组试验数据及现场观测数据拟合得到;另行搜集包括苏通大桥、杭州湾跨海大桥、妈狱跨海大桥、瓯江大桥在内的36组国内外试验及实测数据,根据泥沙粒径分为两组,验证该公式在泥沙粒径范围为0.255~0.7 mm及0.008~0.2 mm的海床条件下的精度,并与65-1修正式、65-2修正式、HEC-18方程、韩海骞公式对比分析。结果表明,该公式相对误差控制在-28%~+34%以内,较65-1修正式、65-2修正式精度有明显提高,对处于水深、流速大、泥沙粒径小的特殊环境下的跨海桥梁钢管桩基础冲深预测展现出较好的适用性,能为公路桥梁技术人员提供一定参考。

