基于CFD-FEM的浮式结构水弹性响应数值模拟

刘 一，朱仁庆，程 勇，谢 彤，李润泽

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212001)

超大型浮体是一种综合性的海洋浮式结构物，在维护国家海洋权益方面有极其重要的作用[1]。超大型浮体水平尺度与垂向尺度相差非常大，是一种极为扁平的柔性结构物，过大的尺度差异导致其弯曲刚度降低，其弹性变形相比于船舶与其他海洋结构物不能被忽略，因此必须采用水弹性方法分析超大型浮体在流体载荷作用下的变形以及浮体变形对流场的影响。过去对浮体水弹性的求解方法是基于Bishop等[2]提出的二维水弹性力学理论，通过将复杂的海洋结构物简化为梁模型,以模型的干模态叠加来表达结构的运动与变形,建立流固耦合运动方程，计算海洋结构物的水弹性响应。由于二维水弹性理论在计算时忽略了船宽对流体运动的干扰，Wu[3]将三维适航性理论与三维结构动力学理论相结合,提出可适用于分析波浪中任意三维弹性体的三维水弹性理论。杜双兴[4]提出了零航速三维振荡源格林函数快速计算方法,使得三维水弹性分析工作可以在PC机上进行，并建立了完善的三维航行船体线性水弹性力学频域分析方法[5],从而可不受浮体细长比和航速的限制。Murai等[6]提出了将大型浮体处理成多个小结构组合的计算方法，并将数值计算与试验数据对比，两者之间有良好的一致性。王大云[7]采用三维时域格林函数,推导出应用于弹性体的三维势流时域积分方程，建立了三维水弹性时域分析理论。Watanabe等[8]讨论了超大型浮体(VLFS)锚链系统、海域海底的变化以及结构数值模型的选取，并进一步探讨了未来VLFS研究的方向。陈徐均[9]建立了浮体二阶水弹性力学分析方法,并推导锚泊浮体三维线性及非线性频域水弹性力学运动方程，开发出计算系泊浮体的计算程序。付世晓[10]将刚性浮体的锚泊系统动力分析理论与三维水弹性理论相结合，推导并建立了能够考虑浮体弹性影响的锚泊系统动力响应分析方法，并编制了相应的计算程序。

目前主要采用势流理论对各类浮式结构物的水弹性响应进行计算分析。由于其对波浪破碎、砰击等现象难以数值模拟，且忽略了流体黏性的影响，因而对强非线性波浪运动及其引起的结构大幅运动和变形不能精确模拟，对结构物近壁面的压力变化也不能准确捕捉。相比于势流理论，计算流体动力学(CFD)在描述流场中速度场与压力场的改变，捕捉自由液面处波浪的非线性现象等方面有更高的精度和准确性。方昭昭等[11]在计算波浪对航行船舶水动力的影响时发现，相比于势流计算结果，计算流体动力学方法更能真实的反映模拟流场，并且CFD方法计算结果更加精准。

随着计算流体动力学的发展，如何采用CFD模拟海洋结构物与流体的耦合作用得到越来越多学者的关注。Ley等[12]开发了一种基于雷诺时均N-S方程(RANS)方法的CFD和动态FEA的单向和双向耦合系统，并证明了CFD方法和动态FEA耦合技术可以很好地预测由规则波和不规则波激励引起的载荷。Seng[13]采用OpenFoam开发了一种耦合方法，使用梁模型进行水弹性响应的计算，结果证明CFD方法在估算结构的水弹性响应方面具有良好的准确性。Tomoki等[14]使用CFD-FEA技术分析了6600TEU集装箱船的水弹性响应，并计算了船体中剖面弯矩的变化，与三维水弹性方法进行比较，有良好的一致性。但是流体与结构之间的耦合是采用单项耦合，由于仅考虑单向耦合计算，不能实现流体与结构之间的双向数据传递。

采用CFD-FEM方法实现双向流固耦合，计算非线性波浪与弹性浮板的水弹性响应问题。首先，基于CFD方法建立黏性数值水池，采用速度入口造波原理模拟五阶Stokes波浪；使用FEM方法对弹性浮板进行离散，建立弹性浮板与外部流场的交界面。计算过程中，浮板表面的压力载荷通过数据映射的方式传递给有限元计算模块的浮板模型，模型在压力载荷的作用下发生形变，并将变形后的模型数据传递给CFD计算模块，对流固耦合表面进行更新，在新的交界面上再进行流体质点速度场与压力场的计算，在下一时间步内重复此步骤。在计算过程中CFD和FEM两模块的数据进行实时交互，从而实现交界面上浮板的运动与弹性形变协调。此外，还探讨了在不同参数下，如浮板厚度、入射波波幅以及浮板的三维效应对弹性浮板水弹性响应的影响。

1 数值模型

1.1 控制方程

1.1.1 流体控制方程

当不考虑流体的压缩性，不计流体表面张力时，使用连续方程与N-S方程来描述海洋工程问题中的黏性流体运动：

·u=0

(1)

(2)

式中：u为速度矢量，ρ为流体密度，p为压力，g表示重力矢量，μ为黏度系数，其为动力黏度系数μfluid与涡动黏度系数μt之和。

1.1.2 结构控制方程

假设结构为线弹性材料，在波浪等外载荷作用下相对于原平衡位置做刚体运动和变形，其结构运动方程通过有限元方法得到：

(3)

式中：m为结构质量矩阵，c为结构阻尼矩阵，k为结构刚度矩阵，x为节点位移列阵，F(t)为外界各种力合成的等效节点力列阵。

对于线弹性材料而言，其应力应变关系为线性关系，由胡克定律给出：

σ=Dε

(4)

式中：D为材料正切系数，σ为应力，ε为应变。

1.2 数值方法

1.2.1 湍流模型

在求解工程实际问题时，通常将连续方程与N-S方程各项取时均，此时N-S方程成为雷诺时均N-S(RANS)方程。在求解RANS方程时，由于引入涡动黏度系数μt，将导致方程不封闭，需引入湍流模型来进行计算。在海洋工程计算中，SST k-ω模型在方程中增加了交叉扩散项，并且在湍流黏性系数中考虑了剪切应力的影响，使其计算稳定性好，计算效率与计算精度较高，故计算中使用的湍流模型为SST k-ω模型。SST k-ω模型的输运方程为：

(5)

(6)

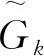
1.2.2 数值造波方法

非线性波浪相比于线性波浪而言，其波峰较陡，波谷较为平坦，呈现出的是一种非对称曲线，更加符合现实中的实际波浪。选取五阶波浪Stokes进行波浪的模拟；在数值水池造波边界处，流体质点的速度和波面瞬时升高满足式(7)～(10)中的条件。

五阶Stokes波的波面方程为：

(7)

x方向的速度为：

(8)

z方向的速度为：

(9)

在式(7)～(9)中的各项系数为：

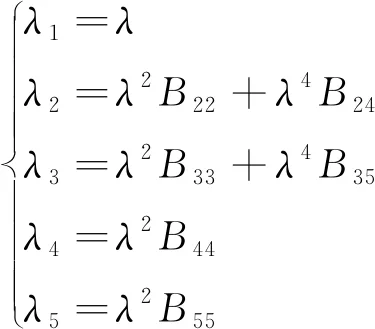
(10)

式中：ω′为圆频率，k′为波数，d为水深；参数c的定义为c=cosh(kd)；式(10)中的参数在文献[15]中对各项有详细的计算过程与定义。

1.2.3 数值消波方法

对数值水池而言，常规的消波方法是在水池的尾部出口位置加设消波区域，以消减在出口边界上的波浪反射对计算区域的影响。但是考虑到由于水池中浮式结构物的存在，在波浪冲击到物体上时，会产生反射波浪，并在一定程度上影响到速度入口造波的准确性。为消除物体反射波浪以及水池出口处的反射波浪对速度造波入口边界的影响，将在水池入口区域与出口区域都设置消波区域，如图1所示。在图1的数值水池入口消波区采用强迫波形消波方法(wave forcing)，通过在动量方程中增加源项来实现波形的强制。

在其入口消波区域的动量方程中增加的源项为：

qφ=-γρ(φ-φ*)

(11)

式中：γ为阻尼系数，φ为动量方程的数值求解结果，φ*为理论计算的数值求解结果。

在图1的数值水池出口消波区采用阻尼消波的方法(wave damping)，通过在波浪运动的垂直方向上增加阻尼以增强波浪的耗散。在动量方程中附加的阻尼源项为：

(12)

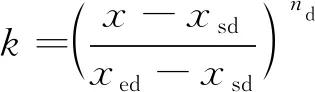
(13)

式中：u3为在垂向的速度分量；f1,f2分别为线性阻尼项与非线性阻尼项；nd为沿波浪传播方向上的阻尼系数，nd的取值参考文献[16]；xsd,xed分别为阻尼区域开始位置坐标与结束位置坐标。

图1 数值水池消波区域Fig. 1 Area of wave damping in numerical tank

1.3 耦合方法

在耦合计算中，采用CFD和FEM之间的双向耦合方法，该过程在图2中进行简要说明，图中的t0为初始时刻，Δt表示每个耦合内的时间增量。在初始时间使用CFD计算出浮板表面的压力以数据映射的方法传递给有限元模块中的浮板模型，在压力载荷的作用下，浮板有限元节点产生速度与加速度的变化，将导致流固耦合交界面变形；之后把变形后的节点数据传递给CFD计算程序，进行交界面的更新。由CFD计算出的压力场和速度场以及FEM计算出节点的速度和加速度将传递给下一时间步。耦合计算中数据映射至关重要，因为CFD与FEM之间的网格离散不同，网格节点不相对应，计算中的数据映射采用形状函数插值的方法进行。

图2 CFD-FEM双向耦合流程Fig. 2 Flowchart of two-way coupling of CFD-FEM

2 数值计算

2.1 计算模型验证

计算模型与文献[17]中的一致，弹性浮板模型参数见表1。由于数值水池前端设置了消波区，浮体前端与数值水池入口处的间距可以缩短，这里选择为L；浮体尾端到数值水池出口处的距离为1.5L；为减少水池两侧边界对计算的影响，设置浮体到水池两侧边界的距离为2B。入射波波高Hw=0.02 m，波长分别取λ=2 m与λ=4 m。流场采用正六面体网格划分，弹性浮板采用四面体单元划分。为了提高数值模拟精度，在自由液面上下波动空间和弹性浮板所在区域及附近流域内进行了网格加密。流场网格与结构单元划分如图3所示。在流体与结构交界面上，流场网格节点与单元节点不重合，在计算过程中，在交界面上进行数据映射，实现计算数据的同步交互。

表1 弹性浮板模型参数Tab. 1 Model parameters of floating plate

图3 计算流域网格及弹性浮板单元划分Fig. 3 Meshing of numerical tank and plate

图4为弹性浮板在迎浪端垂向位移最大时，浮板中线处的无因次垂向位移，并与文献[17]中试验数据与文献[18]中势流计算结果进行比较；其中浮板中线位置是指浮板宽度上的中心位置，而无因次化的垂向位移为节点垂向位移与波幅的比值。由此可见，计算结果与两者的结果吻合较好，说明CFD-FEM方法能有效模拟弹性浮体在非线性波浪下的运动，采用CFD-FEM方法模拟非线性波浪作用下超大型浮体水弹性响应具有可行性。

图5为波长2 m时，弹性浮板中线处迎浪端垂向位移时历曲线。可以看出，在8 s之后，浮板迎浪端的垂向位移达到较为稳定的状态，相邻两个垂向位移峰值处的时间间隔与入射波的波浪周期相同，为T=1.13 s；同时选取弹性浮板运动的稳定时间段内3个相邻迎浪端垂向位移最大处的时刻，对比在3个时刻下中线各点处的垂向位移差异(初始时刻为T0=9.17 s)，从图6中可以发现，在垂向运动稳定时间段内，在固定的波浪周期间隔之间，弹性浮板中线各处的垂向位移保持一致，3个相邻时间间隔内的垂向位移数值差异很小。这是由于在规则波浪下，随着计算时长的增加，浮板弹性变形运动趋于稳定，相邻时间间隔内的垂向位移差异较小，图中3个时刻的弹性变形保持一致。

图5 弹性浮板中线迎浪端垂向位移时间历程Fig. 5 Variation of time series of vertical displacement at fore-end of the elastic plate

图6 3个相邻时刻下的浮体中线垂向位移Fig. 6 Vertical displacement of VLFS at three adjacent moments

2.2 波高对浮板水弹性响应的影响

研究入射波波高对弹性浮板水弹性作用的影响，选取在给定的入射波长λ=2 m与λ=4 m时，3种不同入射波高下(H=0.02 m，0.03 m，0.04 m)，弹性浮板中线处迎浪端、中部与尾端位置处的垂向位移时间历程结果，分别如图7和图8所示。

图7 λ=2 m时弹性浮板在不同波高条件下的垂向位移时间历程Fig. 7 Vertical displacement of time series of the plate at fore-end, mid-position and back-end for different wave heights with λ=2 m

图8 λ=4 m时弹性浮板在不同波高条件下的垂向位移时间历程Fig. 8 Vertical displacement of time series of the plate at fore-end, mid-position and back-end for different wave heights with λ=4 m

从图7与图8可见，在两种波长条件下，弹性浮板各点的垂向位移随着波高的增加而增加。这是由于当入射波波高增大时，浮板各点处受到的波浪载荷增加，浮板的水弹性响应加剧，导致浮板各位置处的垂向位移数值增加。

在波长2 m时，入射波的周期为1.13 s，图7中截取时间段8 s与14 s之间稳定段的迎浪端、中部以及尾端3个位置处垂向位移的时间历程。在此时间段内，浮板各点处的垂向位移变化趋于稳定，3个不同波高下的垂向位移峰值虽有较大的差异，但是三者垂向位移变化周期是保持一致的。这是因为当入射波的波浪周期确定后，波幅的变化只会影响弹性浮板水弹性响应的剧烈程度，对其运动的周期无较大的影响。在图8中，波长4 m时各点处的垂向位移变化周期要远大于波长2 m时的变化周期，但是其不同波高下的各点垂向位移周期也趋于一致。

在迎浪端位置处，两个波长下不同波浪幅值时的垂向位移峰值基本一致，这是因为迎浪端垂向位移的变化主要是受到入射波的影响，其运动状态与波浪基本保持一致，浮板其他位置处的垂向位移变化对迎浪端的影响较小。

相比于入射波波长λ=2 m而言，较大的入射波长λ=4 m时的中部与尾端的垂向位移增加的更为明显，这是由于波长4 m时，浮板迎浪端与尾端的距离为1倍的波长，当浮板的迎浪端处在波浪的波峰(波谷)位置处，浮板两端同时存在较大的垂向位移，从而导致中部位置的垂向位移也进一步加剧；而在波长2 m时，浮板迎浪端与尾端的距离为1.5倍的波长，当迎浪端处在波浪波峰(波谷)位置处，尾端位于波浪波谷(波峰)位置处，浮板的迎浪端与尾端存在相反的垂向位移，从而导致浮板中部的水弹性响应减弱，并没有出现较大的抬升。在同样波长下，波高的增加会引起弹性浮板总体弹性变形运动的加剧，而波长与浮板长度的关系，在一定程度上会影响弹性浮板内部各点处的最大垂向位移变化。

2.3 板厚对水弹性响应的影响

研究弹性浮板的板厚对浮板水弹性作用的影响，选取在给定入射波波高、波长时，3种不同浮板厚度(d=0.06 m，0.10 m，0.14 m)下，迎浪端、中部和尾端3个位置处的垂向位移时间历程，结果如图9所示。当模型材料属性(弹性模量与泊松比)未发生改变时，随着弹性浮板厚度的增大，浮板的截面弯曲刚度也随之增加。

从图9(a)与图9(c)可以看出，在浮板迎浪端与尾端位置处，垂向位移的变化趋于一致，3种不同板厚在浮板自由端位置处垂向位移虽有差异，但数值相差较小。这是由于在浮板自由端位置，入射波的波浪载荷对浮板弹性变形运动的影响要远大于截面弯曲刚度的影响，从而导致在自由端处的垂向位移幅值与入射波的波幅相一致。在图9(b)的浮板中部位置处，厚度d=0.14 m情况下，浮板中部节点的垂向位移峰值要小于厚度为d=0.06 m与d=0.10 m处的垂向位移峰值。这是因为在浮板中部位置，弯曲刚度对浮板弹性变形的影响要大于波浪载荷的影响，当浮板的板厚增加时，截面弯曲刚度也随之增加，导致中部节点的垂向位移逐渐减少，整体的水弹性响应也进一步减弱。

综上所述，浮板厚度的改变会影响弹性浮板的水弹性响应运动，对浮板中部位置的影响要远大于对自由端位置的影响。当浮板厚度在一定范围内变化时，自由端的垂向位移峰值不会出现较大的变化。

图9 弹性浮板在不同板厚条件下的垂向位移时间历程Fig. 9 Time series of the plate at fore-end, mid-position and back-end for different values of plate thickness

2.4 弹性浮板的三维效应

当弹性浮板在入射波浪的作用下出现弹性变形运动时，由于浮板中线位置处的波浪载荷与两侧自由端处的波浪载荷之间存在一定的差异，将导致浮板各位置处的垂向位移存在一定的差异。图10为入射波高为H=0.04 m，波长λ=4 m时，浮板中间位置，以及两侧自由端处垂向位移。

在图10中可以看出，弹性浮板中间位置处各节点的垂向高度要高于两侧自由端位置处的垂向高度，而对于两侧自由端而言，两者的垂向高度趋于一致。

从图11的垂向位移云图中同样可以看出，浮板各点垂向高度从中间位置向两侧自由端逐渐降低，两侧的位移云图以浮板中心位置处呈对称分布。

图10 浮板不同位置处的垂向位移(迎浪端位移最大)Fig. 10 Vertical displacement at different positions of the plate

图11 浮板不同位置处的垂向位移云图(迎浪端位移最大)Fig. 11 Vertical displacement at different positions of the plate

3 结 语

利用CFD建立数值黏性水池，并采用速度入口造波方法完成五阶Stokes波浪的模拟；通过对弹性浮板进行有限元离散，并在外部流场与结构之间的交界面上进行数据交互，实现双向耦合的同步计算。通过与文献中的数值计算结果和试验结果进行比较，表明该数学模型可以较准确地模拟弹性浮板在非线性波浪作用下的弹性变形运动。

研究发现：在板厚不变，入射波幅增加时，浮板的水弹性响应运动也随着加剧，浮板各点的垂向位移随波幅的增加而增加；在给定波浪环境时，浮板自身厚度的变化对浮板的垂向位移有一定的影响，在浮板厚度变化时，迎浪端与尾端两处的自由端垂向位移并没有随浮板厚度出现较大的改变，而浮板内部节点随厚度的增加，其垂向位移减小；在浮板两侧自由端位置处的垂向高度相比于中间位置的垂向高度稍小，浮板的垂向高度从中间位置向两侧逐渐减小。

CFD-FEM方法在计算大型浮体在非线性波浪环境下的水弹性响应时具有较好的精度，今后可以采用此方法进一步分析不均匀海底平面与不规则波浪对大型浮体水弹性响应的影响。