盾构隧道下穿管道施工引起的管道水平位移研究
管凌霄 徐长节 可文海 丁海滨 张高锋 虞巍巍


摘 要:采用两段法研究了盾构隧道下穿管道施工引起的管道水平变形特性,在第1阶段改进了Loganathan公式,求得盾构隧道以任意角度下穿管道施工引起的管道轴线处土体水平位移,第2阶段采用Vlasov模型模拟管土相互作用,并求得管道水平位移解析解。通过与工程监测数据及有限元计算结果的对比,验证了方法的正确性,并进一步分析了管道与隧道夹角、管道直径以及隧道埋深对管道变形的影响。结果表明:盾构隧道斜下穿管道施工时,隧道与管道相交角度的大小对管道水平位移造成的影响显著,随着夹角的减小,管道的水平位移逐渐增加;当管道与隧道相交角度较小时,盾构隧道开挖引起的管道水平位移相对管道竖向沉降不可被忽略;随着管道直径的增大、隧道埋深的增加,盾构隧道斜交下穿管道施工引起的邻近管道变形均减弱。
关键词:盾构隧道;管道位移;管道;两阶段方法;相互作用
中图分类号:U455.43;TU433 文献标志码:A 文章编号:2096-6717(2020)06-0054-09
Abstract: The two-stage method is used for analyzing the pipeline deformation caused by the underneath shield tunneling. In the first stage, the Loganathan formula is modified for studying the ground loss when the tunnel axis intersection with the pipeline axis is not orthogonal. The soil-pipeline interaction is studied based on the Vlasov model in the second stage, and the pipeline deformation is also obtained. Then, through comparison with the finite element results, the proposed method was verified to be correct. The influences of pipeline diameter; tunnel depth and intersection between the tunnel and pipeline on pipeline deformation have been further studied. The parametric study shows that the intersection angle of the tunnel and the pipeline significantly influences the pipeline horizontal displacement, and the pipeline deformation increases remarkably as the intersection angle decreasing. The parametric study indicates: a. the pipeline horizontal displacement cant be ignored compared to the pipeline vertical displacement when the intersection angle of the tunnel and the pipeline is relatively small; b. the pipeline deformation is weakening as the pipeline diameter and tunnel depth increasing.
Keywords:shield tunnelling; displacement of pipe; pipe; two-stage method; interaction
盾構隧道在掘进过程中会引起地层损失[1],使邻近管道产生变形甚至破坏。城市地下管道是城市的生命线,如何全面分析盾构隧道开挖对邻近管道变形的影响,成了城市地铁工程中亟待解决的热点问题[2-3]。
目前,在盾构隧道下穿管道施工引起的管道变形理论研究中,两段法是常用方法[4],即将盾构隧道开挖对邻近管道变形的影响研究分为两个阶段[5]:第1阶段分析盾构隧道开挖引起的管道轴线处土体位移;第2阶段将管道位置处的土体位移转化为荷载施加到管道上,再采用合理的弹性地基梁模型模拟管土相互作用求解出管道变形的解析解。第1阶段中,Loganathan等[6]提出盾构隧道开挖引起邻近土体位移的计算公式因其具有良好的计算精度被广泛应用[7-8];在第2阶段中,通常采用弹性地基梁理论分析管土相互作用,而地基模型以Winkler地基模型和Pasternak地基模型为主[9-10]。张治国等[7]采用Loganathan公式研究了邻近盾构隧道开挖对既有软土隧道的影响;魏纲等[9]利用可考虑土中剪力的Pasternak模型研究了双线隧道开挖引起的管道竖向位移。虽然Pasternak模型在Winkler模型的基础上计入了土中剪力传递,被广泛应用于研究土结构相互作用问题[11-12],但Pasternak模型的缺点在于其关键参数只能采用试验或经验公式估算,无法通过准确的数理推导求得,而考虑地基土沿变形方向衰减变形的Vlasov地基模型能在理论上更好地解决这个问题[13]。施成华等[14]采用Vlasov地基模型分析基坑开挖对邻近单桩的影响;刘建文等[15]采用Vlasov地基模型计算了基坑开挖引起下卧地铁隧道的隆起变形量。除了理论研究之外,在试验研究方面,Vorster等[16]进行了隧道开挖对邻近地埋管道影响的离心模型试验;在数值分析方面,张治国等[17]采用两阶段解析方法并结合有限元数值模拟了类矩形盾构隧道开挖对邻近管线竖向位移的影响;在工程实例研究方面,孙宇坤等[18]对某沿海城市盾构隧道下穿管道施工引起管道沉降的监测数据进行了分析。
众多学者对盾构隧道开挖引起邻近管道竖向位移的问题进行了大量分析,但对于盾构隧道开挖引起管道水平位移的研究还鲜有学者涉及。根据Deane等[19]对Heathrow Express Trial Tunnel的监测结果,土体的水平位移最大可达22.5 mm,Plamer等[20]对Thunder Bay隧道的监测结果显示,土体最大水平位移可达34 mm。如此大的土体水平位移会引起显著的水平向管土相互作用,此时,只考虑竖向管土相互作用无法真实模拟管道的变形情况。因此,有必要针对盾构隧道开挖引起的邻近管道水平位移进行相关研究。笔者拟采用两段法,在第1阶段改进Loganathan公式求取了隧道与管道以任意夹角相交情况下盾构隧道开挖引起邻近管道轴线位置处的土体水平位移;第2阶段采用Vlasov弹性地基梁模型模拟水平向管土相互作用并求解盾构隧道下穿邻近管道施工引起的管道水平位移解析解。随后,将计算结果与工程实测值及有限元模拟结果进行对比验证,并深入分析了隧道与管道夹角、管道直径及隧道埋深等因素对管道水平位移的影响。
1 水平向管土相互作用分析
盾构隧道开挖时,邻近土体自由场会产生竖向及水平向位移,由于已有研究多是隧道轴线与管道轴线垂直相交的工况,该工况下盾构隧道开挖引起的土体水平位移对管道的作用转化成了管道的轴力,以至于盾构隧道开挖对邻近管道的影响可忽略。但隧道轴线与管道轴线以非垂直方式相交时,盾构隧道开挖引起的土体水平位移对管道产生的作用为具有一定角度的水平力,具体管道的受力模式见图1。
图1(a)为盾构隧道开挖引起的土体水平位移示意图。从图1中可以看出,管道与隧道以非垂直的角度相交时,隧道开挖引起的土体水平位移以一定的角度作用在管道上。图1(b)为管道受力示意图,图中P为土体水平位移对管道造成的外力,Px为外力P在X轴方向上的分力(平行于管道),Py为外力P在Y轴方向上的分力(垂直于管道)。从图中可看出,当隧道與管道以非垂直的方式相交时,盾构隧道开挖引起的土体水平位移对管道造成的外力可分解为垂直和平行于管道轴线方向的两个分力,其中,垂直于管道轴线的分力Py会使管道产生水平向的位移。基于此,采用两阶段法对盾构隧道下穿管道施工引起的管道水平位移进行求解。
2 土体水平位移求解
2.1 盾构隧道开挖引起的土体水平位移
1998年Loganathan提出了盾构隧道开挖引起邻近土体位移的解析解,其计算结果与实测值十分吻合。根据Loganathan公式,盾构隧道开挖引起邻近的土体水平位移可以表示为[6]
2.2 邻近管道轴线位置的土体水平位移
3 管道水平位移的求解
3.1 管道水平位移控制方程
图4为Vlasov地基模型。该模型与Pasternak模型同为双参数模型,但该模型的土体参数可以通过具体的数学公式求得,并且考虑了地基土沿着变形方向上的衰减变形。其中地基水平反力p(x)与管道水平位移u(x)的关系为
7 结论
改进Loganathan公式计算了盾构隧道开挖引起邻近管道轴线位置处的土体水平位移,基于考虑土中剪力传递的Vlasov模型得出了土体自由场中管道的水平位移解析解,经过分析得出以下结论:
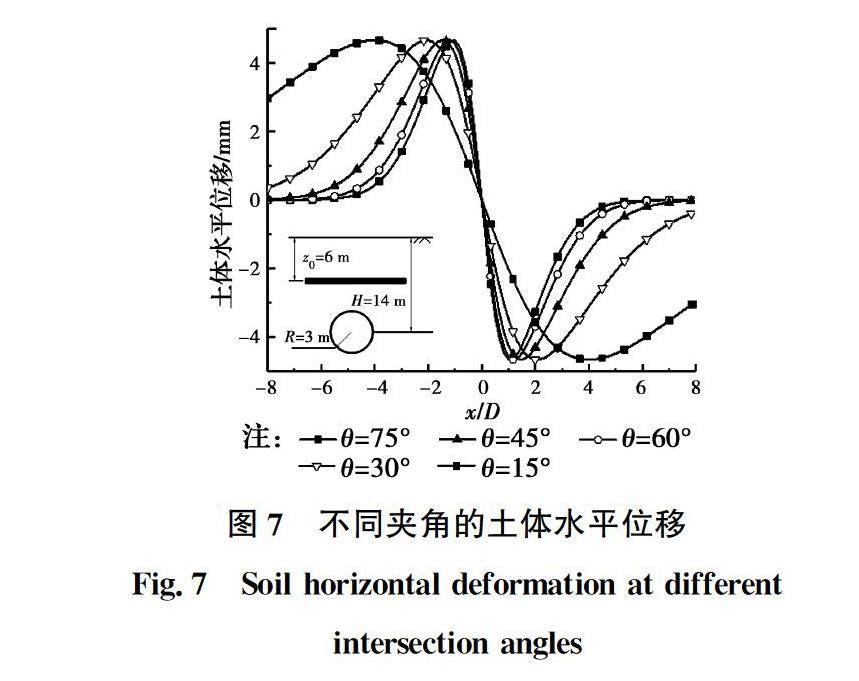
1)盾构隧道开挖方向与管道轴线的夹角对管道水平位移的影响比较显著。随着夹角角度的逐渐减小,盾构隧道开挖引起的水平位移逐渐增大。
2)在θ=15°时管道水平最大相对位移值可达到了8.988 mm,为竖向最大相对位移的46.28%,说明在管道与隧道相交角度较小时,盾构隧道开挖引起的管道水平位移不应被忽略。
3)控制其余参数不变,管道直径的增加会导致管道的变形程度减弱、相对位移(包括竖向及水平)最大值的减小;隧道埋深的增加会减弱盾构施工对管道造成的影响。
4)从管道的弯曲应变来看,盾构隧道下穿管道施工时,引起的管道水平向最大压应变超过了竖向最大压应变。因此,对于极限压应变较小的管道,更应关注管道的水平向变形特性。参考文献:
[1] XIANG Y Z, LIU H L, ZHANG W G, et al. Application of transparent soil model test and DEM simulation in study of tunnel failure mechanism [J]. Tunnelling and Underground Space Technology, 2018, 74: 178-184.
[2] KLAR A, MARSHALL A M. Linear elastic tunnel pipeline interaction: the existence and consequence of volume loss equality [J]. Géotechnique, 2015: 1-5.
[3] 马少坤, 刘莹, 邵羽, 等. 盾构双隧道不同开挖顺序及不同布置形式对管线的影响研究[J]. 岩土工程学报, 2018, 40(4): 689-697.
MA S K, LIU Y, SHAO Y, et al. Effects of twin shield tunneling with different construction sequences and different relative locations on adjacent pipelines [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 689-697. (in Chinese)
[4] KLAR A, VORSTER T E B, SOGA K, et al. Soil: pipe interaction due to tunnelling: comparison between Winkler and elastic continuum solutions [J]. Géotechnique, 2005, 55(6): 461-466.
LIU J W, SHI C H, LEI M F, et al. Analytical method for influence analysis of foundation pit excavation on underlying metro tunnel [J]. Journal of Central South University(Science and Technology), 2019, 50(9): 2215-2225. (in Chinese)
[16] VORSTER T E B,MAIR R J,SOGA K,et al. Centrifuge modelling of the effects of tunneling on buried pipelines: Mechanisms observed [C]//Proceedings of the 5th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, Amsterdam, the Netherlands, 2005: 27-33.
[17] 張治国, 师敏之, 张成平, 等. 类矩形盾构隧道开挖引起邻近地下管线变形研究[J]. 岩石力学与工程学报, 2019, 38(4): 852-864.
ZHANG Z G, SHI M Z, ZHANG C P, et al. Research on deformation of adjacent underground pipelines caused by excavation of quasi-rectangular shields [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 852-864. (in Chinese)
[18] 孙宇坤, 吴为义, 张土乔. 软土地区盾构隧道穿越地下管线引起的管线沉降分析[J]. 中国铁道科学, 2009, 30(1): 80-85.
SUN Y K, WU W Y, ZHANG T Q. Analysis on the pipeline settlement in soft ground induced by shield tunneling across buried pipeline [J]. China Railway Science, 2009, 30(1): 80-85. (in Chinese)
[19] DEANE A P, BASSETT R H. The heathrow express trial tunnel [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1995, 32(8): A411.
[20] PALMER J H L, BELSHAW D J. Deformations and pore pressures in the vicinity of a precast, segmented, concrete-lined tunnel in clay [J]. Canadian Geotechnical Journal, 1980, 17(2): 174-184.
[21] LIANG R Z, XIA T D, HUANG M S, et al. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect [J]. Computers and Geotechnics, 2017, 81: 167-187.
[22] 塞尔瓦杜雷. 土与基础相互作用弹性分析[M]. 范文田,等. 译. 北京: 中国铁道出版社, 1984.
SELVADURALA P S. Elastic analysis of soil-foundation interaction [M]. Translated by FAN W T, et al. Beijing: China Railway Publishing House, 1984. (in Chinese)
[23] 可文海, 管凌霄, 刘东海, 等.盾构隧道下穿管道施工引起的管土相互作用研究[J]. 岩土力学, 2020, 41(1): 221-228, 234.
KE W H, GUAN L X, LIU D H, et al. Research on upper pipeline-soil interaction induced by shield tunnelling [J]. Rock and Soil Mechanics, 2020, 41(1): 221-228, 234. (in Chinese))
[24] 吴为义, 孙宇坤, 张土乔. 盾构隧道施工对邻近地下管线影响分析 [J]. 中国铁道科学, 2008, 29(3): 58-62.
WU W Y, SUN Y K, ZHANG T Q. Analysis of the effects on the adjacent underground pipelines by shield tunneling construction [J]. China Railway Science, 2008, 29(3): 58-62. (in Chinese)
(编辑 胡玲)

