渐近搜索算法在软土基坑基底抗隆起上限分析中的应用

洪利 仉文岗

摘 要：潜在破坏面的确定是软土基坑基底抗隆起上限分析的难点与重点。在传统的上限分析法中，破坏面仅假设与基坑开挖宽度有关。而采用渐进搜索算法确定破坏面，无需假设破坏面具体形状，通过多次迭代计算即可确定临界破坏面，且该算法已在边坡稳定与可靠度分析中成功应用。介绍了应用多块体上限法分析基坑抗隆起稳定性的基本步骤，并详细介绍了渐进搜索算法的流程，针对基坑抗隆起分析问题的特点，对渐进搜索算法中的初始破坏面生成、搜索边界、收敛准则等重新进行了设置;针对搜索过程中遇到的问题，给出了解决方法。通过实例分析检验渐近搜索算法的实际应用效果，并围绕算法中的初始搜索步长、破坏面结点个数、搜索次数等关键参数进行讨论，给出建议取值。案例分析表明，渐近搜索算法在软土基坑基底抗隆起上限分析中应用效果很好，且相比于其他的上限分析方法，渐近搜索算法计算简单，无需假设破坏面形状参数。

关键词：Monte Carlo方法;渐近搜索算法;多块体上限法;基坑稳定性;极限分析

中图分类号：TU 432 文献标志码：A 文章编号：2096-6717（2020）06-0046-08

Abstract： Determining the potential failure surface plays an important role in basal stability analysis of braced excavations in soft clay by upper bound method. For traditional upper bound method， it is assumed that failure surfaces are only related with excavation width. However， for progressive search method， the critical failure surfaces can be evaluated by multi-iterations without assuming detailed shape of failure surfaces. And this method was successfully applied to slope stability analysis. Firstly， this paper introduced the step of basal stability analysis of excavation via multi-block upper bound method. Secondly， this paper illustrated the framework of progressive search method. Considering the characteristic of basal stability analysis of excavation， the generation of initial failure surfaces， the search boundary and the convergence criteria are reset. And some solutions are proposed to deal with the problems during search process. Moreover， this paper verifies the performance of progressive search method by case studies， and proposes conclusions about search length， number of pointsat the failure surface and number of searches. At last， this paper concludes that progressive search method is applied in basal stability analysis successfully. And compared to other upper bound method， progressive search method without assuming detailed shape of surfaces is easier to calculate.

Keywords：MonteCarlomethod; progressive search method; multi-block upper bound method; basal stability; limit analysis

基坑坑底抗隆起穩定性验算是软土地区基坑设计的重要内容之一。目前，基坑抗隆起计算主要包括极限平衡方法[1-4]、强度折减有限元法[4-6]和上限分析法[7-8]。上限分析法源于Drucker[9]提出的极限分析理论，Chen等结合岩土材料的特性，将上限分析法应用于边坡的稳定性分析和地基承载力分析[10-15]。上限分析法主要有上限分析有限元[16]、多块体法[14]、连续速度场[8]等多种实现手段。其中，上限分析有限元法最为复杂，需要编制完整的有限元程序，目前，暂无成熟的上限分析有限元软件，因此，多以后两种计算方法为主。连续速度场需预先假设破坏面中的一些参数，因此，计算结果的准确性很大程度上依赖于假设参数的合理性。多块体法不需预先假设破坏面，可以很好地与渐近搜索算法结合。

渐近搜索算法是先利用Monte Carlo思想随机生成初始破坏面，然后利用“单个结点搜索+整体搜索”的方法，通过多轮搜索，使初始破坏面逐渐逼近临界破坏面，目前已成功运用于边坡稳定与地基承载力上限分析的破坏面搜索中[11，14]。笔者主要描述基坑抗隆起上限分析中的破坏面搜索技术，并给出破坏面搜索的优化问题表达;对搜索程序中的关键参数调试进行说明，最后通过实例计算与对比分析检验渐近搜索算法的应用效果。

1 多块体上限法计算基坑抗隆起稳定性

1.1 上限分析基本原理

极限分析上限定理有多种表示方法，此处采用能量方程表达式，即对于任何运动许可的破坏机构，内能耗散率不小于外力功功率，如式（1）。

1.2 运动许可机构建立及相容速度场计算

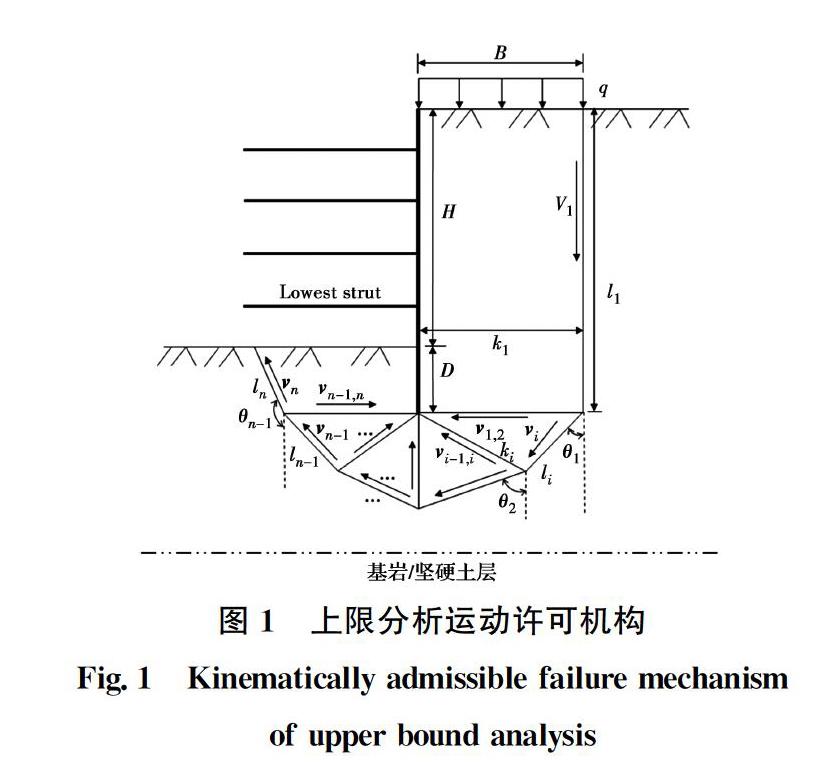
参考极限平衡法与强度折减有限元法所分析得到的基坑隆起破坏面，以及Goh[3]、Faheem等[6]、秦会来等[7]所做研究，假设内支撑与支护墙体构成的支护系统具备足够的刚度（即暂不考虑支护系统刚度的影响），因此，墙后土体的破坏面轨迹竖直向下，其余部分则采用“近似圆弧滑动法”，如图1所示。

如图1所示，许可机构以圆弧滑动面为主要参考对象，破坏面由n+1个结点构成，共有多边形块体n个（其中2个四边形块体，其余为三角形块体）。为保证计算的准确性，运动许可机构的圆弧部分应用足够数量的三角形块体。图1中：B为基坑宽度;H为开挖深度;D为支护结构嵌入深度;li为各块体的破坏面长度;ki为各块体之间接触面长度;相容速度场由vi、vi，i+1构成，vi为各块体破坏面处的速度矢量，vi，i+1为相邻块体之间接触处的速度矢量;θi为vi+1正方向与竖直向下方向的夹角。相容速度场满足矢量运算法则由式（2）可知，式中的3个速度矢量恰好构成矢量三角形，由于功率方程计算中只用到速矢量的相对大小，可令v1=1，由算法给出初始破坏面后，所有速度矢量方向均为已知，此时，依据矢量三角形计算法则即可依次求出所有速度矢量的大小。速度矢量的详细计算及推导，可参考秦会来等[15]、邹广电[17]的相关文献。

1.3 功率方程的建立

由式（1）知，功率方程包含方程左端的外力功率和右端内能耗散项。外力功率项主要包括地面超载和土体自重两两部分。内能耗散项主要包括块体破坏面处内能消耗、块体之间接触面处内能消耗、支护结构与土体接触面内能消耗3部分。如式（3）所示。

1.4 安全系数的计算

2 渐近搜索算法的实现

2.1 破坏面搜索过程的优化问题表述

由以上的计算过程可知，不同的破坏机构，具有不同的速度场，安全系数也不同。所以，破坏面的搜索过程实质上可以归结为求安全系数最小值的问题，其中，破坏面的形状、相容速度场大小及方向等均为约束条件。优化表达见式（5）。

目标函数为FS （xi，yi），通过不断更新各节点坐标，使FS取得最小值。约束条件有两个：1）块体节点坐标自右向左为单调不增数列（x1=x2为墙后土体破坏面竖直向下段，-B≤xn为保证破坏面不穿越支护结构截面的几何条件）;2）保证θi为单调递增数列，在搜索过程中维持破坏面“上凹”。Goh等[18]、陈祖煜[19]、张鲁渝等[20]指出，在边坡破坏面的搜索中，破坏面的上凹会自动实现，无须将保持破坏面上凹作为约束条件;Greco[11]、秦会来等[14]则建议在边坡搜索过程加入保持破坏面“上凹”为约束条件。考虑到基坑的破坏面较边坡复杂，笔者在编制计算程序时对两种方法均进行了测试，根据最后的计算结果，加入“上凹”约束条件具有更高的计算效率，建议在搜索程序中加入此约束条件。

2.2 初始破坏面的确定

初始破坏面既可以人为指定，也可以随机生成， Greco[11]、秦会来等[14]、陈祖煜[19]均采用4结点随机生成的初始破坏面;考虑到基坑破坏面较复杂，本文采用7结点随机初始破坏面。参考软土基坑抗隆起稳定性分析方面已有的研究成果，控制初始破坏面在水平方向上边界为0.5B～1B。由式（6）～式（19）可计算出初始破坏面各处结点的坐标值。

2.3 破坏面的搜索

破坏面的搜索分为结点搜索和整体搜索两个阶段。结点搜索阶段主要确定破坏面的形状和大小，而整体搜索阶段主要确定破坏面的大小。

2.3.1 结点搜索阶段 结点搜索主要是针对每个结点逐个搜索;如图2所示，每个结点给定8个方向（地表和开挖面的结点只允许水平方向移动），依次进行搜索，只要有一个方向搜索成功，即更新该结点的坐标，并进入下一个结点的搜索;若所有方向搜索均失败，则该结点的坐标保持原值，并将该结点的搜索步长减半。“搜索成功”是指该结点沿某方向移动后破坏面的安全系数减小。

2.3.2 整体搜索阶段 考虑到结点搜索的先后顺序会对最终的搜索结果造成影响，在结点搜索的基础上，增加整体搜索阶段。具体做法是，在依次完成8个节点的搜索后，加入一轮整体搜索，即破坏面整体“外扩”或“内缩”;坐标更新公式为式中：i为结点序号;k为搜索的次数（依次搜索完各结点计为一次）。

坐标更新后，安全系数减小，则保留更新后的结点坐标;否则，将保留原坐标值。重复进行结点搜索与整体搜索，满足收敛准则后，可认为搜索完成。

搜索算法流程图如图3所示。图3所示为7结点破坏面搜索流程，在实际求解过程中，往往7个结点不够，必须具备一定数量的结点，才能够捕捉到破坏面的几何特征。因此，学者们提出了多种扩充结点的方法，笔者采用张鲁渝等[20-22]建議的办法，即初始破坏面采用较少的结点，先进行数次搜索，破坏面初步稳定后;在每段滑面的中点处内插结点进行第2轮、第3轮的计算，直至安全系数及破坏面达到收敛条件。每一轮的计算流程与图3所示7结点计算流程相同。

另一方面，搜索算法还可能会陷入局部最优解的情况，从而搜索不到全局最优解[14，19]。为避免此问题，可设置多组初始破坏面，再从中选取安全系数最小的一组为最终结果。以3.1节中的算例为例，按式（6）～式（19）计算生成50组初始滑面，如图4所示。

2.4 收敛准则

由图3可知，收敛准则由安全系数差值和搜索步长两个指标构成，且它们均与破坏面结点个数有关，指标阈值由式（22）、式（23）计算。

3 搜索算法應用效果检验

3.1 计算方案及计算参数设置

为检验搜索算法的应用效果，采用9个算例来检测。设置一个标准算例检验算法的可用性，同时，在此基础上设置两组对比算例，观察开挖宽度（4个）和支护结构嵌入深度（4个）对计算结果的影响，将程序计算结果与目前公认的一些结论相比较，初步检验算法的准确性。计算参数见表1。

3.2 算例计算结果分析

算例采用4轮搜索，每轮的结点个数分别为7、11、19、35;根据式（22），4轮的搜索步长阈值设置为10-4、5×10-5、10-5、10-6;4轮的搜索次数分别预设为150、150、100、80。各阶段的搜索结果及破坏面形状见图5和图6。

由图5和图6可知，随着破坏面结点个数的增加，破坏面的形状和安全系数趋于稳定。其中，第3阶段和第4阶段安全系数差值仅为0.003 2，相对误差小于1%，表明搜索算法应用效果较好;且各阶段的收敛速度均很快，可适当减小每阶段的搜索次数。依据图6，建议前3个阶段搜索次数控制在60～80次，第4阶段搜索次数控制在40～60次。由图7也可以观察到，第3阶段和第4阶段的破坏面位置基本一致，因此，搜索算法应控制在3～4轮即可（即破坏面结点个数20～40），不宜过多或者过少。

除标准算例外，设置了两组对比算例，观察支护结构嵌入深度和基坑宽度对安全系数及破坏面的影响，计算结果如图7、图8所示。

由图8可见，随着支护结构嵌入深度的增加，基坑失稳面逐渐扩大，安全系数逐渐提高，符合常规的有限元软件计算结果及工程经验[23-24]。嵌入深度较小时，坑底隆起破坏面可能延伸至整个基坑宽度;嵌入深度较大时，隆起破坏面向支护墙侧靠近，这是因

为假设支护墙体为刚性，因此，增加嵌入深度对阻断隆起破坏面的延伸效果显著。

由图9可见，开挖宽度对基坑抗隆起失稳面影响较大，随着开挖宽度的增加，抗隆起失稳面不断扩大，且失稳面的半径约为开挖宽度的0.9倍，这一结果更倾向于Prandtl失效模式;同时，安全系数也随着开完宽度的增加而减小，这也同样符合常规的有限元计算结果和工程经验[6]。

综合上述的算例分析可以看出，搜索算法在基坑抗隆起分析中具有良好的应用效果。

4 实际工程案例分析

选用唐震等[8]、Chang[25]的案例进行分析。Chang应用上限分析方法重新分析了基坑的抗隆起稳定性，并推导出简易公式用于计算基坑抗隆起安全系数。唐震等采用连续机构场进行上限分析。

计算所需参数以及计算结果见表2（各符号的意义同表1）。

由表2可知，Chang提出的简易计算公式虽然计算简单，但得出的安全系数误差较大，普遍偏小，而且接近临界状态时可能出现误判。唐震等采用的连续机构场法计算结果偏保守，对于重要建筑物的稳定性分析较为适用;而多块体法的计算结果则在两者之间，兼具经济性和安全性的要求。

5 结论

将渐近搜索算法与多块体上限法相结合，实现了基坑抗隆起上限分析。针对多块体上限法的理论要求，给出了初始破坏面的生成公式、几何约束条件与收敛条件;结合算例分析，就破坏面结点个数、搜索步长、搜索次数等参数进行讨论，并给出建议值。为避免出现局部最优解，采用设置多组初始破坏面的方法。通过实例分析以及与其他上限分析方法的对比可知，渐近搜索算法应用效果良好，为解决基坑抗隆起分析中破坏面的确定提供了一种新的计算方法。

笔者在运用算法进行分析时，并未考虑支护结构刚度、基岩埋置深度等因素，因此，如何在上限分析（或安全系数）的计算中考虑这些因素，将是下一步研究的重点。参考文献：

[1] KARL T. Theoretical soil mechanics[M]. Hoboken， NJ， USA： John Wiley & Sons， Inc.， 1943.

[2] BJERRUM L， EIDE O. Stability of strutted excavations in clay [J].Géotechnique， 1956， 6（1）： 32-47.

[3] GOH A T C. Estimating basal-heave stability for braced excavations in soft clay [J]. Journal of Geotechnical Engineering， 1994， 120（8）： 1430-1436.

[4] ZHANG W G，ZHANG R H， WU C Z， et al. Assessment of basal heave stability for braced excavations in anisotropic clay using extreme gradient boosting and random forest regression [J/OL]. Underground Space， 2020， https：//doi.org/10.1016/j.undsp.2020.03.001.

[5] MATSUI T， SAN K C. Finite element slope stability analysis by shear strength reduction technique [J]. Soils and Foundations， 1992， 32（1）： 59-70.

[6] FAHEEM H， CAI F， UGAI K， et al. Two-dimensional base stability of excavations in soft soils using FEM [J]. Computers and Geotechnics， 2003， 30（2）： 141-163.

[7] 秦会来， 陈祖煜， 刘立鹏. 基于上限理论的软土基坑抗隆起稳定分析方法[J]. 岩土工程学报， 2012， 34（9）： 1611-1619.

QIN H L， CHEN Z Y， LIU L P. Basal stability analysis for excavations in soft clay based on upper bound method [J]. Chinese Journal of Geotechnical Engineering， 2012， 34（9）： 1611-1619.（in Chinese）

[8] 唐震， 黄茂松， 袁聚云. 基于连续速度场的基坑抗隆起稳定性上限分析[J]. 岩土力学， 2017， 38（3）： 833-839.

TANG Z， HUANG M S， YUAN J Y， et al. Upper bound analysis of basal stability of excavations based on continuous velocity fields [J]. Rock and Soil Mechanics， 2017， 38（3）： 833-839.（in Chinese）

[9] DRUCKER D C， PRAGER W， GREENBERG H J. Extended limit design theorems for continuous media [J]. Quarterly of Applied Mathematics， 1952， 9（4）： 381-389.

[10] CHEN W F. Limit analysis and soil plasticity [M]. Amsterdam： Elsevier Science， 1975.

[11] GRECO V R. Efficient Monte Carlo technique for locating critical slip surface [J]. Journal of Geotechnical Engineering， 1996， 122（7）： 517-525.

[12] HAN C Y， CHEN J J， XIA X H， et al. Three-dimensional stability analysis of anisotropic and non-homogeneous slopes using limit analysis [J]. Journal of Central South University， 2014， 21（3）： 1142-1147.

[13] GAO Y F， YE M， ZHANG F. Three-dimensional analysis of slopes reinforced with piles [J]. Journal of Central South University， 2015， 22（6）： 2322-2327.

[14] 秦會来， 黄茂松， 王玉杰. 地基承载力上限分析中的Monte Carlo搜索技术[J]. 岩土力学， 2010， 31（10）： 3145-3150.

QIN H L， HUANG M S， WANG Y J. Application of Monte Carlo search technique to bearing capacity calculations by upper bound method [J]. Rock and Soil Mechanics， 2010， 31（10）： 3145-3150.（in Chinese）

[15] 秦会来， 黄茂松. 双层地基极限承载力的极限分析上限法 [J]. 岩土工程学报， 2008， 30（4）： 611-616.

QIN H L， HUANG M S. Upper-bound method for calculating bearing capacity of strip footings on two-layer soils [J]. Chinese Journal of Geotechnical Engineering， 2008， 30（4）： 611-616.（in Chinese）

[16] UKRITCHON B， WHITTLE A J， SLOAN S W. Undrained stability of braced excavations in clay [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2003， 129（8）： 738-755.

[17] 邹广电. 基于一个上限分析方法的深基坑抗隆起稳定分析 [J]. 岩土力学， 2004， 25（12）： 1873-1878.

ZOU G D. Analysis of stability against upheaval of deep excavation by an upper limit method [J]. Rock and Soil Mechanics， 2004， 25（12）： 1873-1878.（in Chinese）

[18] GOH A T C， ZHANG W G， WONG K S. Deterministic and reliability analysis of basal heave stability for excavation in spatial variable soils [J]. Computers and Geotechnics， 2019， 108： 152-160.

[19] 陈祖煜. 土质边坡稳定分析： 原理·方法·程序[M]. 北京： 中国水利水电出版社， 2003.

CHEN Z Y. Soil slope stability analysis[M]. Beijing： China Water Power Press， 2003. （in Chinese）

[20] 张鲁渝， 张建民. 基于Monte Carlo技术的临界滑面搜索算法的实现及改进[J]. 岩土工程学报， 2006， 28（7）： 857-862.

ZHANG L Y， ZHANG J M. Extended algorithm using Monte Carlo techniques for searching general critical slip surface in slope stability analysis [J]. Chinese Journal of Geotechnical Engineering， 2006， 28（7）： 857-862.（inChinese）

[21] 张鲁渝， 张建民. 基于滑面段旋转的Monte Carlo搜索技术及改进（Ⅰ）： 转角大小随机[J]. 岩土力学， 2006， 27（11）： 1902-1908.

ZHANG L Y， ZHANG J M. Modified Monte Carlo techniques by rotating slip segments for searching general critical slip surface（Ⅰ）： Random angle of rotation [J]. Rock and Soil Mechanics， 2006， 27（11）： 1902-1908.（in Chinese）

[22] 张鲁渝， 张建民. 基于滑面段旋转的Monte Carlo搜索技术及改进（Ⅱ）： 常值转角[J]. 岩土力学， 2006， 27（12）： 2197-2202.

ZHANG L Y， ZHANG J M. The extended Monte Carlo techniques by rotating slip segments for searching general critical slip surface （Ⅱ）： Constant angle of rotation [J]. Rock and Soil Mechanics， 2006， 27（12）： 2197-2202.（in Chinese）

[23] 黄茂松， 杜佐龙， 宋春霞. 支护结构入土深度对黏土基坑抗隆起稳定的影响分析[J]. 岩土工程学报， 2011， 33（7）： 1097-1103.

HUANG M S， DU Z L， SONG C X. Effects of inserted depth of wall penetration on basal stability of foundation pits in clay [J]. Chinese Journal of Geotechnical Engineering， 2011， 33（7）： 1097-1103.（in Chinese）

[24] GOH A T C， ZHANG F， ZHANG W G， et al. A simple estimation model for 3D braced excavation wall deflection [J]. Computers and Geotechnics， 2017， 83： 106-113.

[25] CHANG M F. Basal stability analysis of braced cuts in clay [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2000， 126（3）： 276-279.

（編辑 胡玲）