具有多重休假和两阶段服务的MX/G/1重试排队系统

程慧慧, 田中连

(华北水利水电大学数学与统计学院， 郑州 450045)

很多学者对具有Bernoulli单重休假排队系统进行研究, 而对于具有多重休假的排队系统研究较少。 多重休假最初由Levy等[1]提出, 随后得到广泛发展。原小娟等[2]在具有启动时间的二次多选择服务M/G/1排队基础上,引入了空竭服务、多重休假策略,即当系统为空时, 服务台进行一次随机休假, 若休假结束时系统中仍没有顾客排队, 服务台将继续进行下一次随机休假, 直到某次休假结束时系统中有顾客排队。 Kumar等[3]将多重休假和Bernoulli休假相结合, 进一步研究了具有启动失败和Bernoulli多重休假的MX/G/1重试排队系统的性能指标。 贺灵悦等[4]把启动时间引进到多重休假和系统采取Min(N,V)策略控制的M/G/1排队系统中, 讨论了系统队长的瞬态分布和稳态分布。 Rajadurai等[5]引入了多重工作休假的概念, 讨论多重工作休假策略下具有不耐烦顾客和反馈的M/G/1重试排队的重要性能。 Xu等[6]将多重休假运用到多服务台的排队系统中,分析了具有多重休假和不耐烦顾客的M/M/2排队系统队长的分布。

对于具有两阶段服务的排队系统, Kumar等[7]将两阶段服务策略扩展到重试排队系统中,研究带有抢占优先权和两阶段的服务的M/G/1重试排队模型的稳态分布。朱翼隽等[8]也对此类系统进行研究。 后来, Wang等[9]进一步研究了具有二次多选择服务的重试排队系统, 推广了具有二次单选择的重试排队系统。 近年来, Wei等[10]采用嵌入马氏链的方法研究了具有二次可选服务和不耐烦顾客的离散时间Geom/G/1重试排队系统的系统性能。 Varalakshmi等[11]在两阶段服务的基础上, 将即时反馈和G-队列的概念相结合,采用补充变量和矩阵几何解的方法研究了系统稳定状态的概率分布。 徐秀丽等[12]在M/M/1多重休假排队驱动系统的基础上引入可选服务, 采用拟生灭过程探讨第二次服务可选的M/M/1多重休假驱动系统的流排队系统的性能。

近年来,很多学者对两阶段服务的重试排队模型进行研究,但是没有文献研究顾客批量到达、多重休假和二次多选择服务的重试排队模型。 现在两阶段服务的基础上, 引入启动时间和多重休假策略, 考虑了具有启动时间、多重休假和两阶段服务的MX/G/1重试排队系统。 采用嵌入马尔科夫链的方法和补充变量法对系统稳定状态进行分析。

1 模型简介

1.1 到达过程

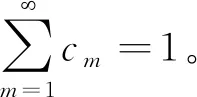
1.2 重试过程

假设系统中无等待区域。 如果批次到达的顾客发现服务台空闲, 则其中一个顾客立即进入第一阶段的服务。 如果顾客到达时发现服务台正在启动或服务状态,则该批次的所有顾客都进入到重试区域进行排队。 假设重试只发生在服务台空闲时刻, 并且只有队首的顾客允许进行重试。 相邻重试时间之间相互独立且具有相同的分布函数A(x), 相应概率密度函数为a(x), Laplace-Stieltjes变换(LS变换)为A*(u)。

1.3 服务过程

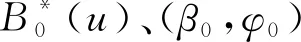
1.4 休假过程

当一次服务结束时, 服务台如文献[3]中描述的Bernoulli休假策略进行休假。 服务台或以概率q进行一次休假, 或以概率p(p=1-q)等待服务下一个顾客。 当服务台完成一次服务时, 若重试区域为空, 则服务台进行一次随机休假。 休假时间独立同分布于函数V(x), 设其密度函数为v(x), LS变换为V*(u), 前两阶矩为v1、v2。 当重试区域没有顾客排队时, 系统总在休假。 如果休假结束时, 重试区域仍为空, 则服务台继续进行下一次随机休假, 直到某次休假结束时, 发现重试区域有顾客在排队, 则立即结束休假进入服务状态。

1.5 启动过程

当服务台休假结束后, 需要一段时间进行启动。 相邻启动时间之间相互独立并且服从分布函数D(x), 概率密度函数为d(x), 其LS变换为D*(x), 第一、二阶原点矩为d1、d2。

2 系统稳定的条件

采用嵌入马尔科夫链的方法对系统稳定状态条件进行分析。令{tn,n∈N}表示第n个顾客服务完成时刻, 或第n次休假结束时刻, 或启动终止时刻,C(t)表示服务台的状态,N(t)为重试区域队长,则Xn={C(tn+),N(tn+)}是状态空间S={1,2,3,4}×{0,1,2,…}∪{(0,0)}上的嵌入马尔科夫链。

定理1嵌入马尔科夫链{Xn,n>0}是遍历的充要条件为

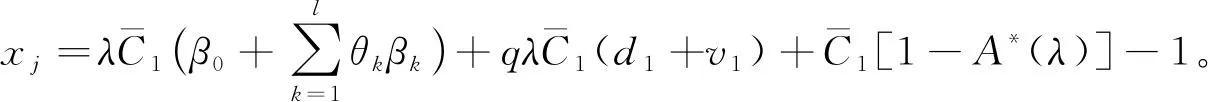
下面证明必要性。 文献[13]中定理1给出了马尔科夫链的非遍历性条件, 即如果序列{Xn}(n≥0)满足Kaplan条件,xj<, 并且存在N使得xj≥0(j≥N), 那么{Xn}(n≥0)是非遍历的。 记P=[pij]为一步转移概率矩阵, 由于存在整数k, 当j0)时,pij=0, 根据文献[13]中定理3知, Kaplan条件满足。 所以不等式保证了马尔科夫链{Xn,n>0}的非遍历性。 则由{Xn,n>0}遍历性得

3 稳定状态概率分布

利用已过时间作为补充变量,建立一个马尔科夫模型,对排队系统稳定状态性能进行分析。

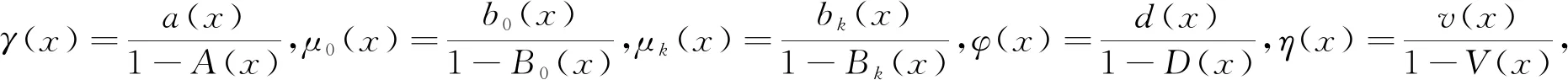
令t→, 则：

采用补充变量法对系统进行分析, 可得到以下的微分方程：

(1)

(2)

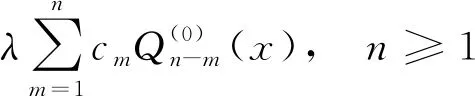
(3)

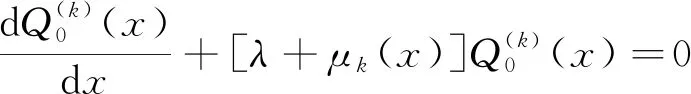
(4)

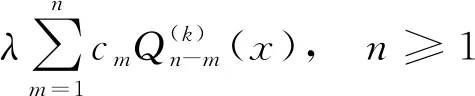
(5)

(6)

(7)

(8)

n≥1

(9)

边界条件为

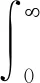
(10)

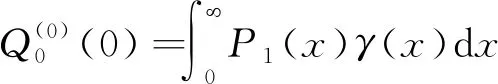
(11)

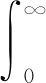
(12)

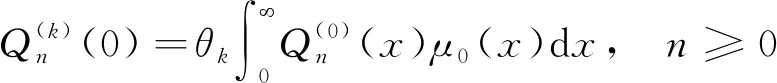
(13)

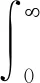
(14)

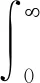
(15)

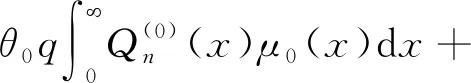
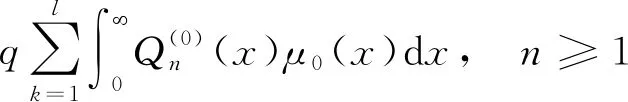
(16)

正则条件为

(17)

为了求解微分方程, 定义下列概率母函数:

定理2在平稳状态下,Xn={C(tn),N(tn)}有以下的概率分布：

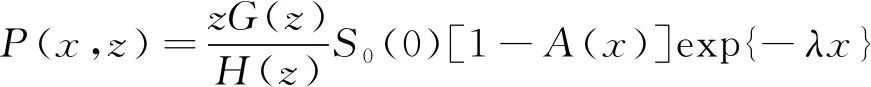
(18)

Q(0)(x,z)=

[1-B0(x)]exp{-λ[1-C(z)]x}

(19)

S0(0)[1-Bk(x)]×

exp{-λ[1-C(z)]x}

(20)

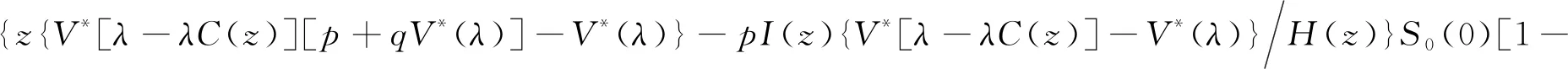
D(x)]exp{-λ[1-C(z)]x}

(21)

S(x,z)={z[p+qV*(λ)]-{p+qD*[λ-

S0(0)[1-V(x)]exp{-λ[1-C(z)]x}

(22)

证明在等式(1)～式(16)两边同时乘以zn,并对n求和可得到：

(23)

μ0(x)}Q(0)(x,z)=0

(24)

μk(x)}Q(k)(x,z)=0

(25)

(26)

(27)

边界条件可变为

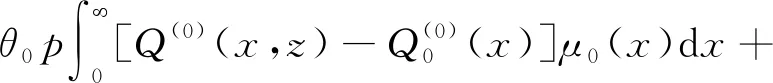
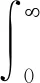
(28)

(29)

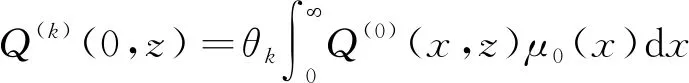
(30)

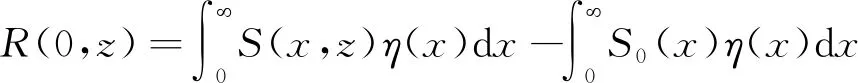
(31)

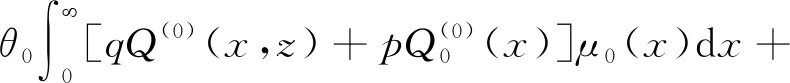
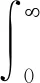
(32)

解式(23)～式(27)可得到：

P(x,z)=P(0,z)[1-A(x)]exp{-λx}

(33)

Q(0)(x,z)=Q(0)(0,z)[1-B0(x)]×

exp{-λ[1-C(z)]x}

(34)

Q(k)(x,z)=Q(k)(0,z)[1-Bk(x)]×

exp{-λ[1-C(z)]x}

(35)

R(x,z)=R(0,z)[1-D(x)]exp{-

λ[1-C(z)]x}

(36)

S(x,z)=S(0,z)[1-V(x)]exp{-

λ[1-C(z)]x}

(37)

从式(8)求解得到：

两边同时乘以η(x)并对x进行积分,有：

(38)

将等式(33)～式(37)代入式(28)～式(32)中, 整理可得到定理2。

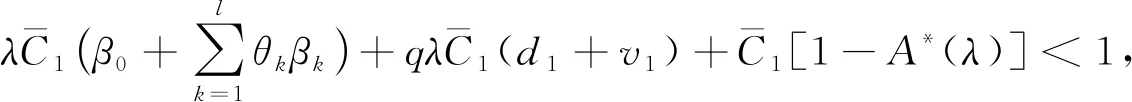
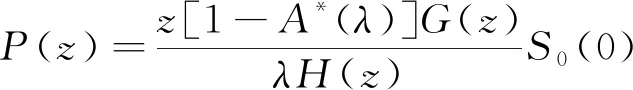
(39)

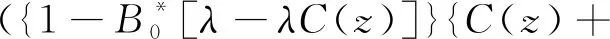
{λ[1-C(z)]H(z)})S0(0)

(40)

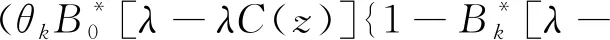
λC(z)]}{C(z)+[1-

C(z)]H(z)})S0(0)

(41)

λC(z)][p+qV*(λ)]-V*(λ)}-

{λ[1-C(z)]H(z)})S0(0)

(42)

qV*(λ)]-{p+qD*[λ-

C(z)]H(z)})S0(0)

(43)

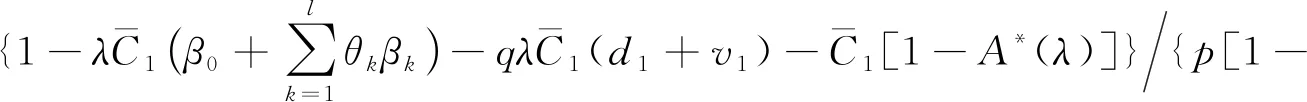
V*(λ)]d1+[p+qV*(λ)]v1}

(44)

对定理2中式(18)～式(22)分别进行上述积分,即可得到定理3。

4 系统相关性能指标

推论1(1)系统中顾客数的概率母函数为

(2)重试区域的顾客数的概率母函数为

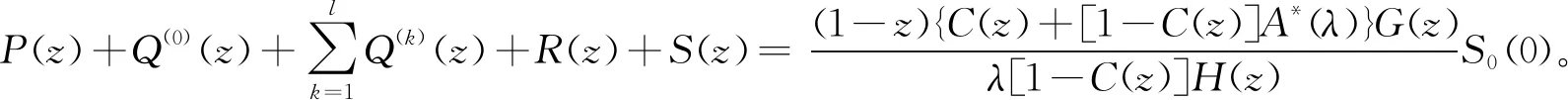
推论2在平稳性条件下, 可得到以下的系统相关指标：

(1)服务台处于空闲状态但系统不为空的概率为

(2)服务台处于繁忙状态的概率为

(3)系统处于启动状态的概率为

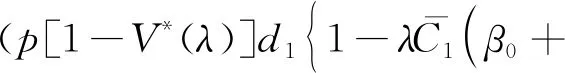
V*(λ)]d1+[p+qV*(λ)]v1}+

(4)系统处于休假状态的概率为

V*(λ)]d1+[p+qV*(λ)]v1}-

Ls=K′(1)=

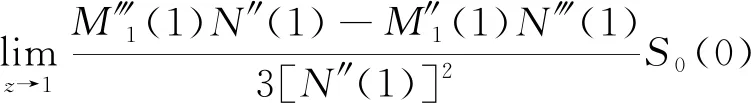
Lq=L′(1)=

其中：

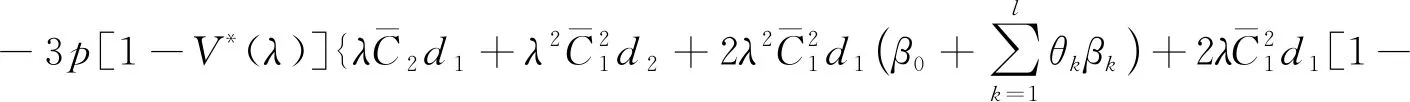
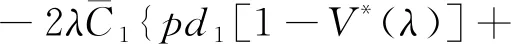
[p+qV*(λ)]v1};

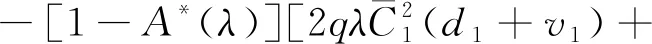
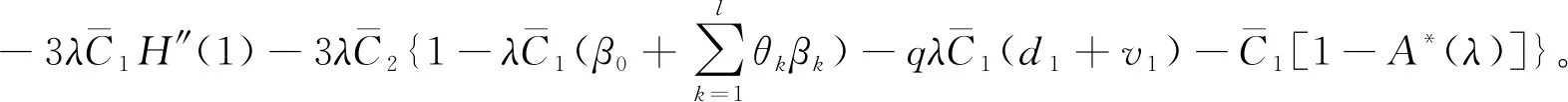
5 数值分析

利用MATLAB通过数值计算, 说明参数对重试区域顾客数的影响。

假设休假时间和服务时间都服从指数分布, 为了使分析更具有一般性, 在重试时间服从以下3种分布。

(1)指数分布：y=ηe-ηx。

(2)埃尔朗分布：y=η2xe-ηx。

(3)超指数分布：y=cηe-ηx+(1-c)η2e-η2x。

在服从这3种情况下进行分析, 选择适当的参数, 在满足定理1的条件下,可得到结果如图1、图2所示。

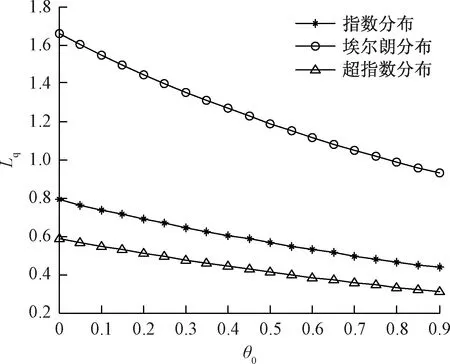
图1 重试区域平均队长(Lq)随概率(θ0)变化图

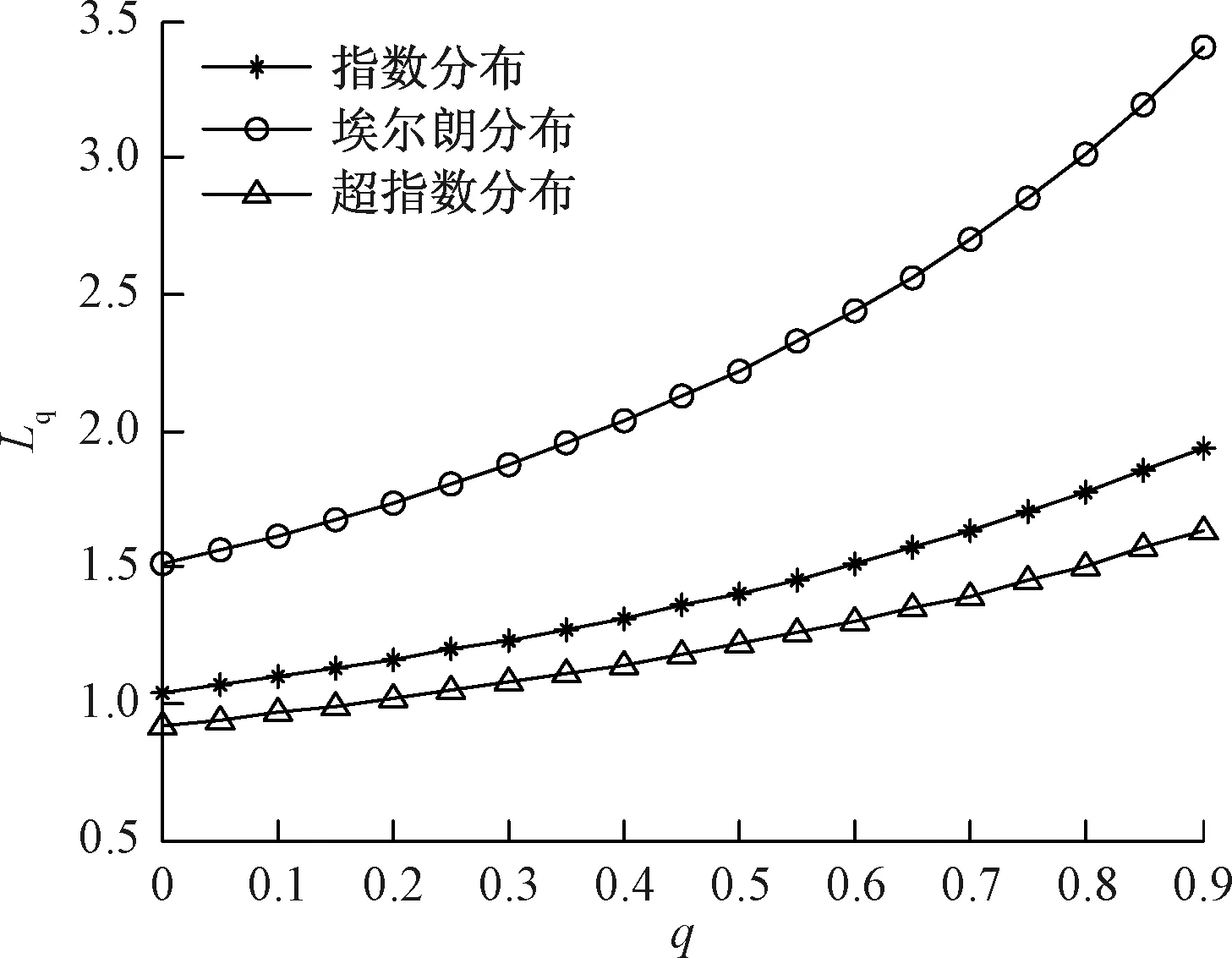
图2 重试区域平均队长(Lq)随休假概率(q)变化图

图1表示重试区域平均队长随着只接受第一阶段服务概率θ0的变化情况,从图1中可以看出：重试区域中顾客平均队长随着只接受第一阶段服务的概率θ0的增加而减少。 随着只接受第一阶段服务后离开顾客的比率增加, 则接受第二阶段服务的顾客减少,从而重试区域排队顾客也相应减少, 这与实际生活中相符合。

图2表示重试区域平均顾客数随休假概率变化情况, 重试区域平均队长随着休假概率q的增加而增加。 随着休假概率q的增加,新到达顾客发现服务台休假,从而进入重试区域的比率也增加,从而重试区域顾客平均队长增加, 实际中也是如此。

6 随机分解

随机分解是休假排队系统的重要研究方法。 休假排队系统中的稳态指标可以分解为经典无休假系统中的相应指标与休假导致的附加指标之和的形式[15]。 令Π(z)为具有两阶段服务的MX/G/1排队系统中顾客数的概率母函数(平稳状态下), 则由文献[7]可知：

引入广义休假的概念, 将重试时间、休假时间和启动时间作为广义休假时间, 也就是广义休假时间从一个顾客服务结束开始到下一次服务开始。令χ(z)表示在广义休假状态下, 任意时刻系统中顾客数的概率母函数, 则

因此可计算出：

λC(z)]S0(0){C(z)+[1-

由推论1可知：

因此可得到K(z)=Π(z)χ(z)。

7 结论

利用嵌入马尔科夫链和补充变量的方法, 得到了系统稳定状态存在的条件, 同时给出了稳定状态时的概率分布和相关系统性能指标。 引入广义休假的概念, 证明了系统的随机分解性。