基于工况识别的安全距离模型

刘 庄， 朱茂桃， 徐晓明， 杨 晗

(江苏大学汽车与交通工程学院, 镇江 212013)

自适应巡航控制系统(adaptive cruise control system,ACC)作为先进的辅助驾驶系统,已经由早期的定速巡航,发展到今天的全速自适应巡航,其广阔的发展前景与巨大的市场需求已经使其成为智能驾驶领域研究的热点之一[1]。自适应巡航系统作为传统定速巡航系统的进一步发展,可以通过车间距控制策略自动调整被控车辆的加速与减速,从而实现正常行驶当中的车速跟随与车距保持,提高了乘坐的舒适性与安全性。ACC系统的安全性重要评价指标是合理的跟车间距,合理的纵向车间距控制算法能够在保证行车安全的同时提高道路使用率[2]。

目前中外学者对安全车间距模型进行了深入的研究,主要提出以下4种经典安全模型：固定安全距离模型[3]、基于制动的安全距离模型[4]、基于车头时距的安全距离模型[5]、基于驾驶员预瞄的安全距离模型[6-7]。其中固定安全距离模型在跟车期间始终保持固定的车间距离,无法适应复杂多变的道路环境；基于制动的安全距离模型是在假设前车制动的前提下建立的安全模型,其跟车间距往往偏大,不利用道路交通流的通畅；基于车头时距的安全模型未考虑前车运动状态对车间距离的影响,不符合驾驶员实际的跟车特性；驾驶员预瞄安全距离模型虽然考虑了驾驶员的主观特性,但往往由于参考样本不足,导致所建立的模型不能准确反映实际驾驶情况。针对上述问题,中外学者纷纷在此基础上作出不同的研究与探讨。余晓江[8]利用模糊与神经网络结合的办法来控制安全跟车距离模型；唐阳山等[9]通过大量试验获得不同驾驶员的制动反应时间,分析了反应时间与车间距离的关系；Li等[10]采用模糊预测控制来确定跟车间距,以上研究均在经典安全距离模型的基础上作出了不同程度的改进,但是仍然忽略了实际行车过程中车辆状态的动态变化,缺乏广泛的自适应性。

现以基于制动过程分析的安全距离模型为基础,针对忽略实际驾驶过程中行车工况动态变化的问题,引入人工神经网络对车辆驾驶状态进行识别,建立基于驾驶工况识别的跟车安全距离模型,最后利用CarSim和Simulink联合仿真对优化后的安全距离模型进行分析验证。

1 基于驾驶工况识别的ACC控制流程

通过识别车辆驾驶工况,实现对纵向安全距离模型的优化,可以得到ACC纵向控制系统流程如图1所示。具体分为如下3个步骤：通过车载传感器采集车辆行驶数据信息,得到工况识别特征参数；根据人工神经网络完成驾驶工况识别；根据工况识别结果确定ACC系统参数,优化安全距离模型,以提高系统的安全性和舒适性。

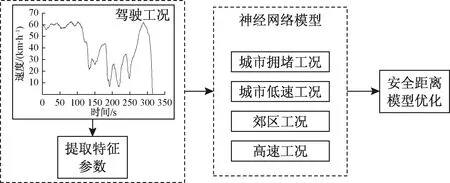
图1 基于工况识别的自适应巡航系统控制流程

2 驾驶工况识别方法

2.1 典型工况数据库的建立

根据人口密度与繁华程度,可以将城市结构大体分为中心区域、次中心区域、近郊区域、远郊区域,其中每一区域的交通状况千差万别。以某城市为例,完成该地区行驶工况数据采集实验,数据采集设备如图2所示。

图2 数据采集设备

依据行驶工况数据采集结果,结合该城市道路类型与交通拥堵状况,将该地区行驶工况划分为4种典型工况：工况1为城市主干道繁华地区,车辆走走停停的严重拥堵工况；工况2为紧邻市中心的次干道生活区域,车辆低速行驶的较拥堵工况；工况3为远离市中心的近郊区域,车辆以较高速度行驶的较统畅工况；工况4为远郊区域,车辆保持高速行驶的通畅工况。各典型工况示例分别如图3所示。

2.2 工况识别参数的确定

车辆在正常行驶中,有众多表征该车辆行驶状态的的特征参数,如车辆最大车速、最大加速度、平均车速、平均加速度、最小车速、最小加速度、行驶距离、怠速时间比等20多个特征参数。但工况识别的特征参数选择过多,导致计算复杂,参数选取过少,又会导致识别不准确的问题。因此,依据前人研究成果,利用各特征参数之间的相关性,选取合适的工况识别参数,其中相关性可由相关系数公式计算得出,具体公式为

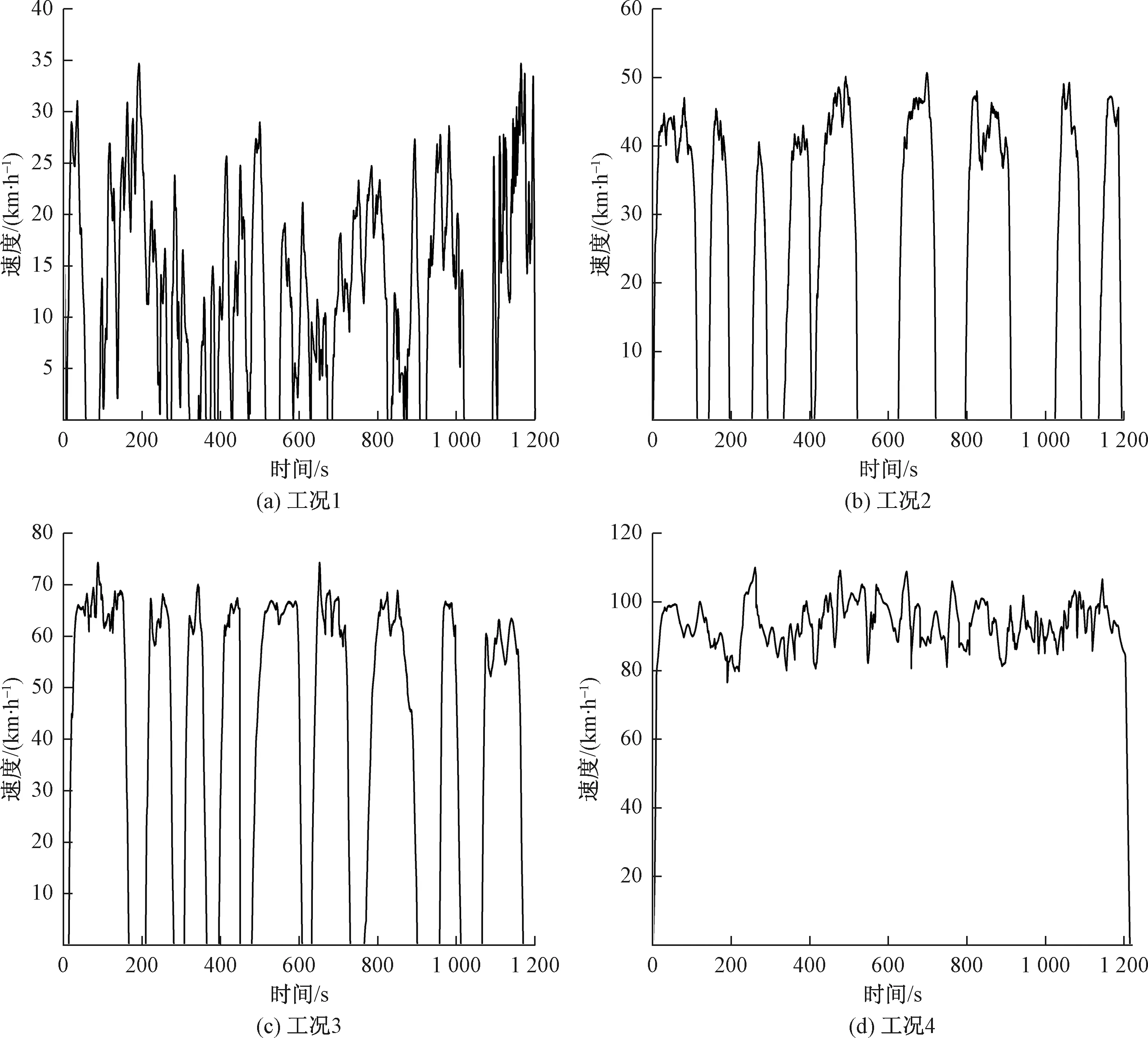
图3 4种典型工况

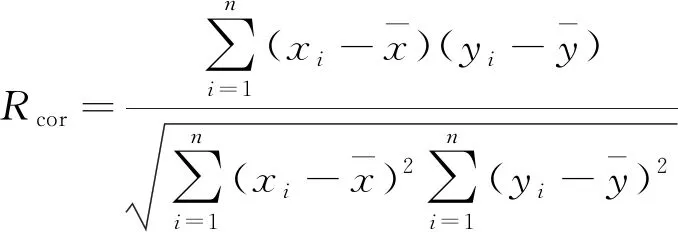
(1)

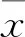
参数间相关系数越大,表征其相关性越好,可以替换;反之,相关系数越小,表征参数间相关性越差,不可替换。最终选取5个最具代表性的特征参数作为工况识别的重要特征参数,其中部分代表工况特征参数如表1所示。

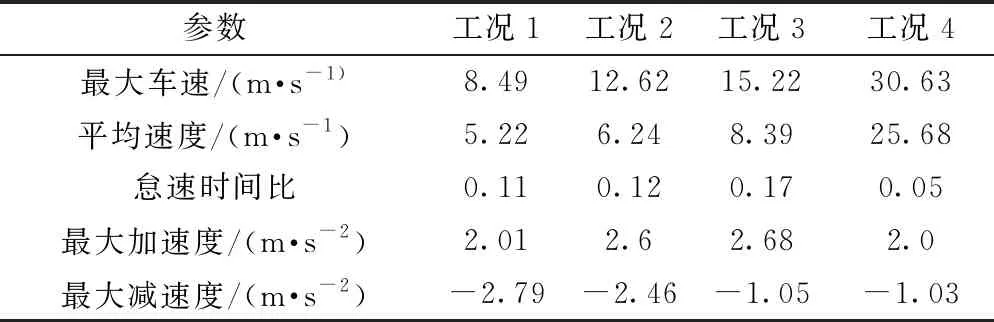
表1 代表工况特征参数

2.3 基于神经网络的模型训练

BP神经网络是由误差反向传播算法训练而来的多层前馈神经网络,凭借其较强的非线性映射能力和柔性的网络结构,广泛应用于各个领域。因此,本文采用该方法应用于行驶工况识别模型训练。BP神经网络主要由3部分组成：输入层、隐含层、输出层,其结构示意图如图4所示。其中输入层作为数据缓存器负责接收外部输入数据,其神经元数目取决于学习样本中输入向量的维数；隐含层作为数据处理的中枢机构,其神经元的个数直接影响输出结果的误差,因此,常依据设计经验和试验进行确定；输出层为数据输出结果,其神经元数量由学习样本中输出向量的维数决定。选择了车辆行驶中的5个特征参数用于工况识别,故输入层有5个神经元,依据隐含层节点计算的经验公式可以确定选择7个隐含节点,经验公式具体如式(2)所示,输出层由行驶工况类型可以确定其神经元数量为4。

(2)

式(2)中:m为输出神经元数量；n为输入神经元数量；b为[1,10]的正整数,由上文可知输入层神经元为5个,输出神经元为4个。因此,隐含层节点范围为4～13,选择7个隐含层节点。

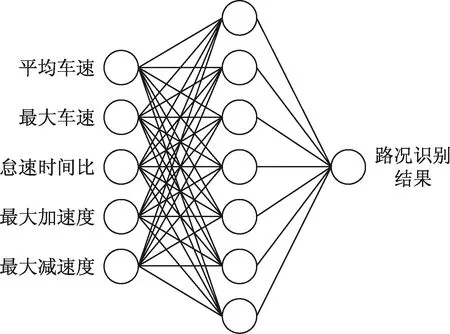
图4 BP神经网络结构

2.4 工况识别方法的确定

车辆行驶时工况识别的方法是分析过去一段时间ΔT内的车辆行驶特征参数信息,依据神经网络模型的分析结果来预测未来一小段时间Δt内的车辆行驶工况,其提取数据的时长和预测数据的时长对计算量的大小和预测结果的误差至关重要。由前人的研究结果表明[11],提取时间ΔT=9 s,预测时间Δt=3 s时,可以实现较高精度的行驶工况识别效果,故采用该时间长度进行工况识别,识别示意图如图5所示。

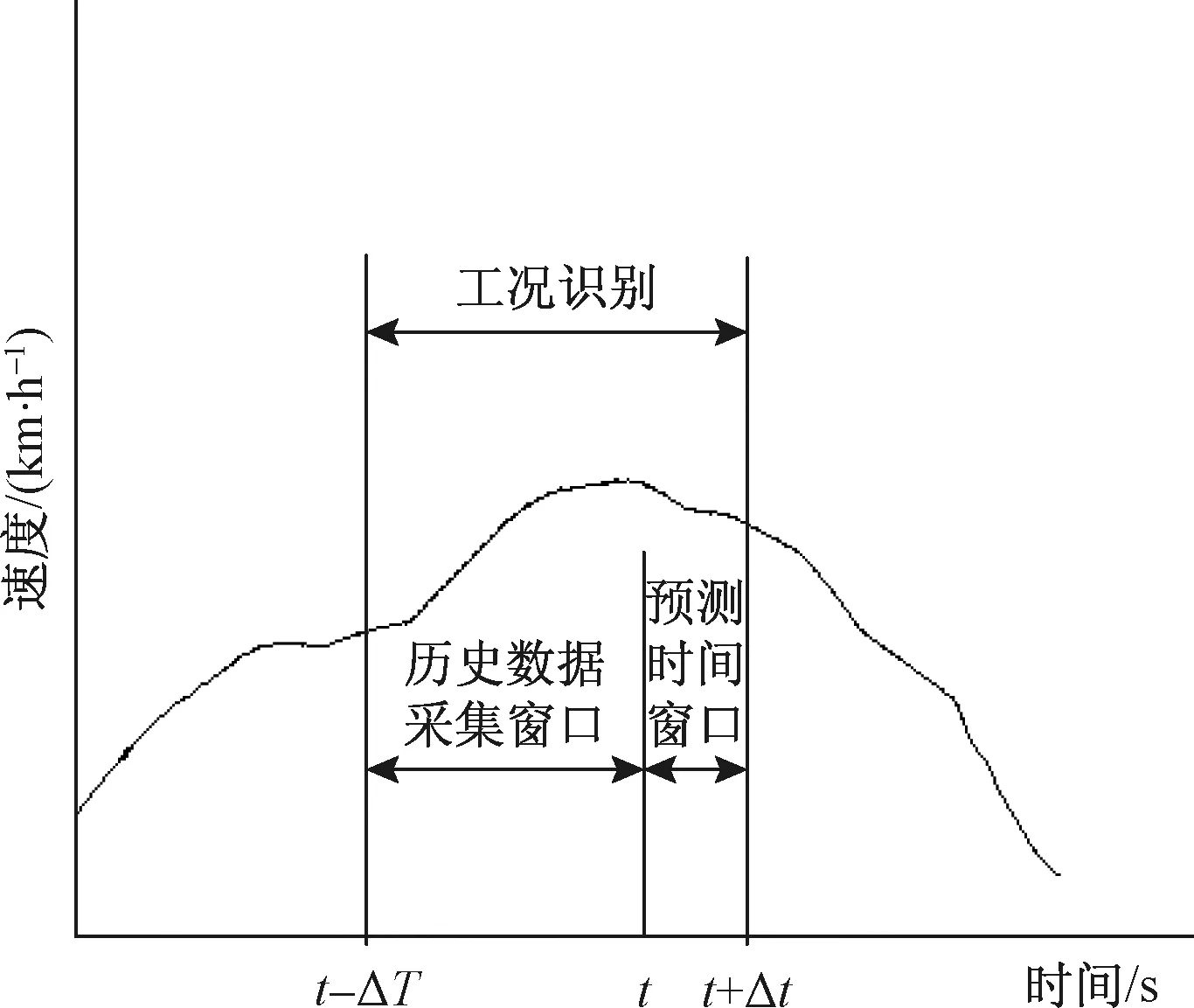
图5 驾驶工况识别示意图

3 跟车安全距离设计

3.1 跟车安全距离模型

车辆在任何工况下跟随前车行驶,首先是以安全为前提,其次是保证道路交通通畅,因此,合理的跟车间距设计作为自适应巡航系统的重要组成部分,对于车辆的纵向安全和道路利用率至关重要。

间距策略设计基于以下假设：①前后两车各方面性能一致；②从自车感知到前车运动状态发生改变到自车采取相应应对措施之前,自车的运动状态保持不变。假设前后两车初始间距为dbr,经过一段时间后两车保持相对静止,前车行驶的距离为d1,自车行驶的距离为d2,两车相对静止间距为d0,该运动过程如图6所示。

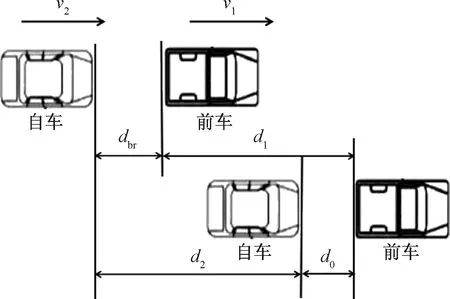
图6 安全距离模型示意图

纵向安全距离D的公式为

D=d2-d1+d0

(3)

前车的一般运动状态主要包括静止、匀速、减速、加速,根据车辆的这四种运动状态与制动过程分别建立安全距离模型如下。

(1)前车静止,自车初始以v2的速度行驶,在发现前车后,经过驾驶员与制动器反应时间T1后保持减速度为a的减速行驶,直至与前车保持相对静止,该段安全距离D可表示为

(4)

式(4)中：T1为驾驶员反应时间和制动器反应时间；T2为制动器持续作用。

(2)前车匀速,前车以速度v1匀速前行,自车以速度v2接近前车,且v2>v1,自车为避免事故发生,以a的减速度接近前车,直至两车保持相对静止,该段安全距离D可表示为

(5)

(3)前车减速,前后两车初始车速分别为v1,v2,随后前车以a1的减速度进行匀减速行驶,后车发现危险后随即采取减速度为a2的制动行为,直至两车保持相对静止时的安全距离D可表示为

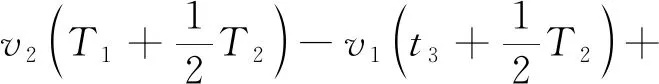
(6)

式(6)中：t3为制动器消除制动间隙时间。

(4)前车加速行驶时,经过分析认为前车匀速行驶的安全模型基本可以满足该工况下的安全跟车行驶。

3.2 安全距离模型优化

前后两车的最小安全距离d0,受较多内外因素的影响,与驾驶员的年龄、驾驶员的性别、驾驶员的经验,车辆行驶速度等密切相关。根据中外相关研究表明,常常将该最小安全距离值取2～5 m中的某一固定值,忽略了车辆的实际行驶工况,因此,提出利用车辆驾驶工况识别结果完成对最小安全距离d0的动态优化。图7所示为驾驶工况识别系数Rc与最小安全距离关系图。其中Rc=1/Rd,Rd为车辆驾驶工况类型。

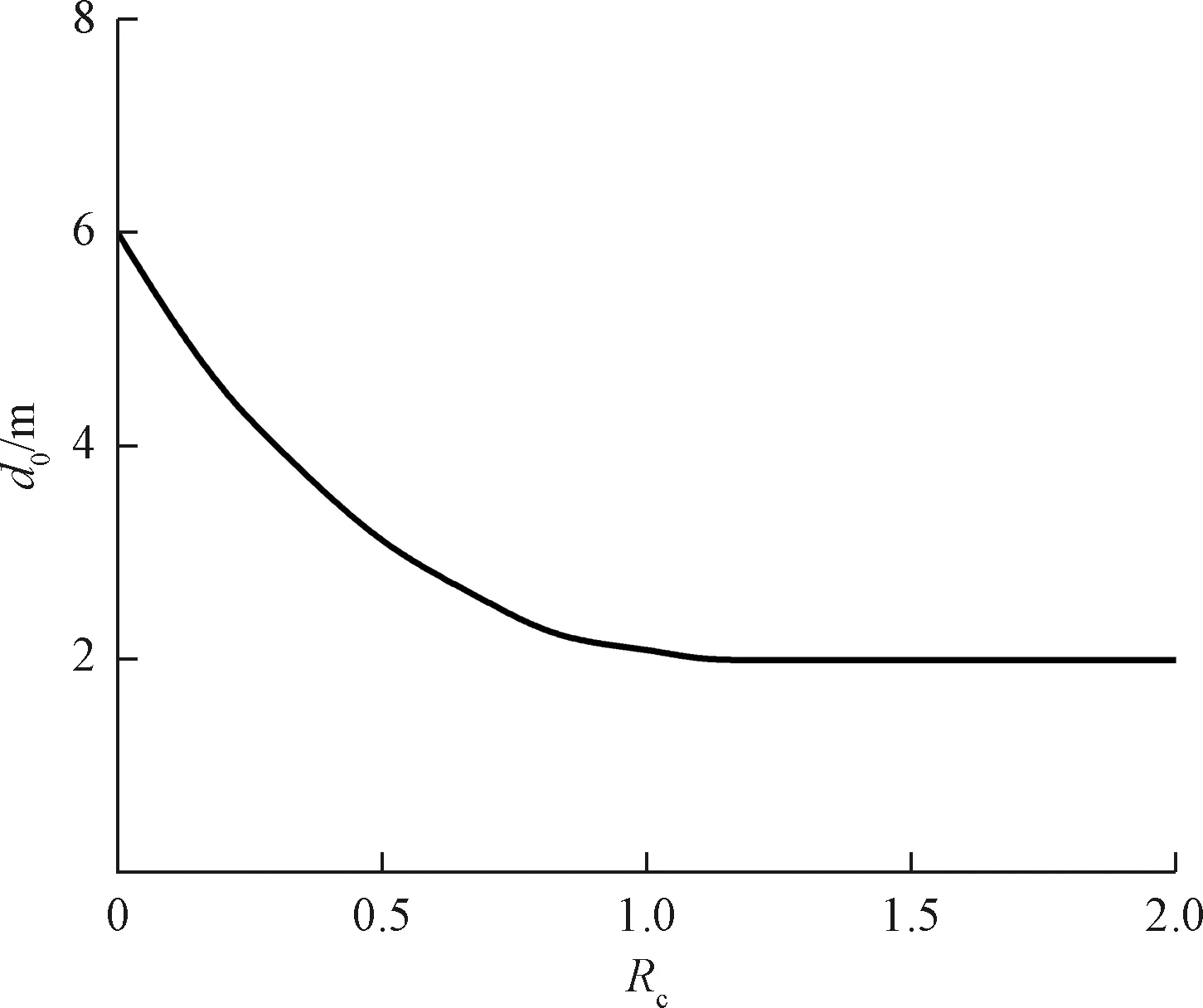
图7 最小安全距离取值

4 仿真结果分析

4.1 行驶工况识别仿真分析

利用MATLAB与工况数据集完成对工况识别模型的训练,将数据归一化处理后输入给模型,选择函数tansig和logsig为传递函数,采用动量梯度下降训练函数trainlm进行训练。模型训练在经过72次迭代,均方误差小于10-6,为迭代最佳效果,到第82次结束训练。

为了验证本文的驾驶工况识别模型的可靠性,基于上述5种特征参数,采用一段随机工况完成对该模型的仿真验证。该段工况数据包括上述4种典型城市工况：城市拥堵工况、城市低速工况、城市郊区工况、城市高速工况。工况识别及安全距离优化结果如图8～图10所示。

由图8、图9可以看出，在1 000 s附近,由于车速较低,将城市郊区工况识别为城市低速工况,在2 125 s附近同样由于车速较低,导致将城市高速工况识别为城市郊区工况,其他时间段识别结果基本正确。由图10可以看出，优化后的跟车安全距离在未优化值附近波动,在高速段其安全距离稍大于未优化前的跟车距离,低速段基本一致或者稍小一些,优化后的跟车安全距离在车辆高速行驶时可以保证足够的安全跟车距离,低速时在满足安全跟车的同时,还可以保证道路车辆的通行率,因此,优化后的安全距离模型具有更好的应用效果。

图8 组合工况仿真

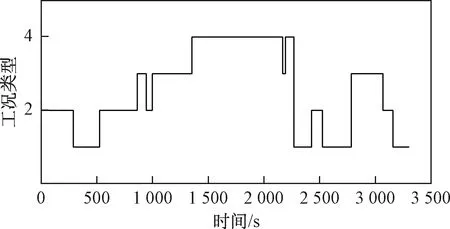
图9 工况识别结果

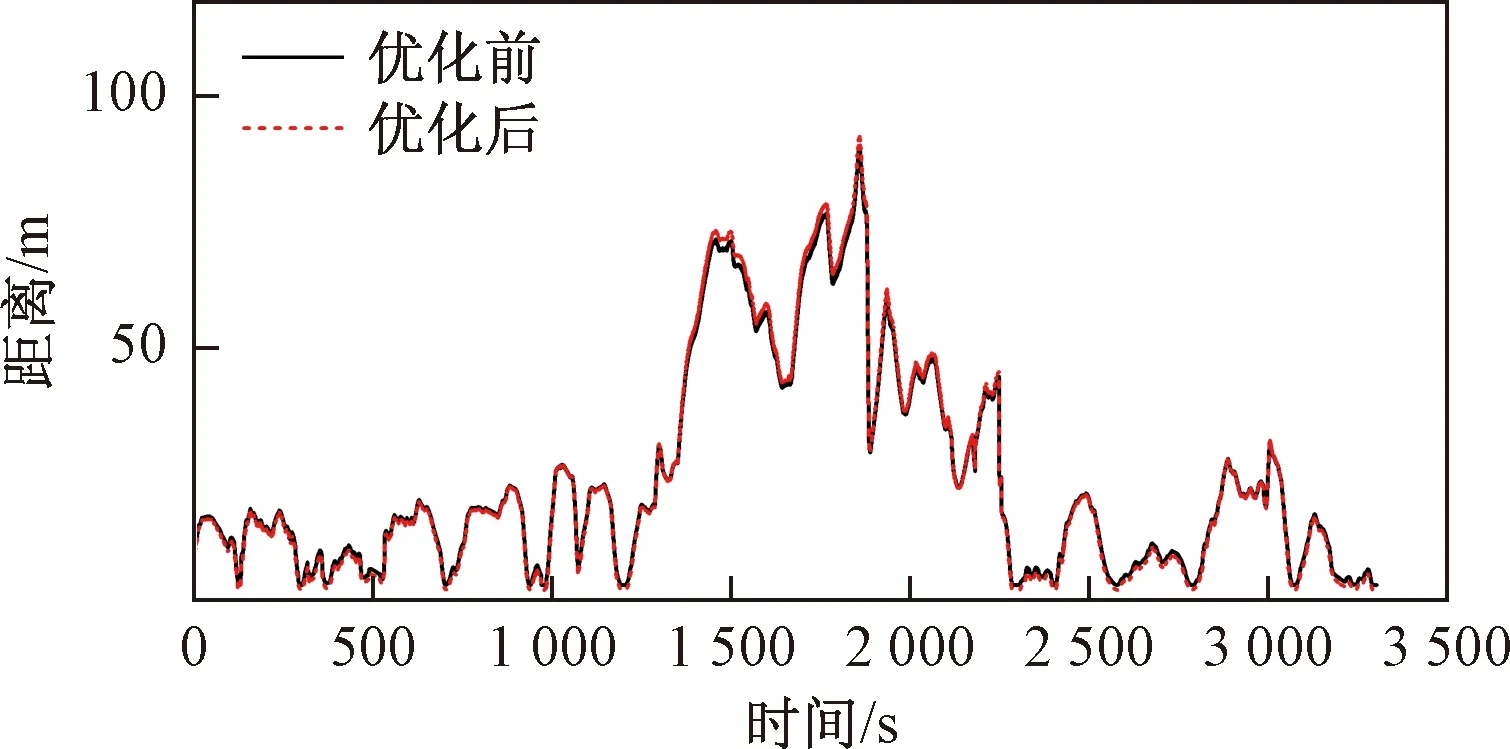
图10 安全距离优化结果

4.2 安全距离模型仿真分析

4.2.1 前车切入

设置仿真场景如下：起初自车与同车道前方车辆保持75 km/h的速度稳定行驶,车距分别为优化前后安全距离模型计算值。在5 s时,旁边车辆低速切入,车速稳定为55 km/h,ACC车辆随即根据相对速度与相对距离采取减速行驶,最终以相同车速与前车保持稳定跟车行驶。仿真结果如图11所示。

由车速变化曲线可知,仿真初期,优化前后的ACC车辆均与前车保持相同速度稳定跟车,当旁边车辆插入本车道后,ACC车辆开始减速行驶,并最终与前车车速保持一致；由车距变化曲线可知,在整个减速过程中,经优化后的跟车距离随工况动态变化,使车辆以较高车速行驶时,具有更高安全系数,低速行驶时,具有更高道路通行率；由加速度仿真结果可知,优化后的ACC车辆最大减速度小于优化前,且整个减速度曲线更为平缓,驾驶员能够很好地适应该工况下的驾驶冲击,舒适性更好。综上所述,在前车低速切入工况下,优化后的ACC车辆在安全性与舒适性上均优于未优化ACC车辆。

4.2.2 前车切出

设置仿真场景如下：起初两车在同车道保持55 km/h的速度稳定行驶,车距为安全距离模型计算出来的距离,在2.5 s时,前车以-2 m/s2的减速度进行减速行驶,随后在4 s时离开本车道,自车进入巡航模式,初始巡航设定车速为75 km/h,仿真结果如图12所示。

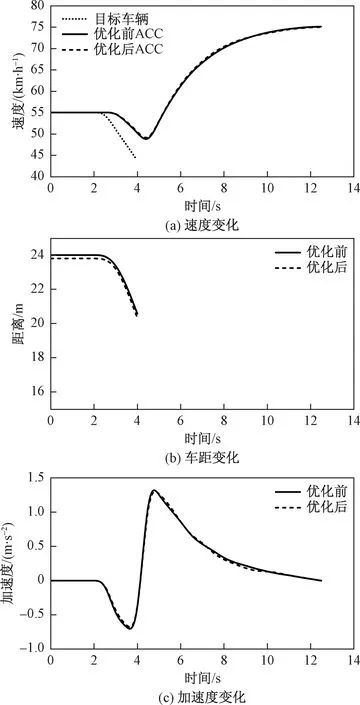
图12 前车切出工况仿真结果

由仿真结果可知,初始时优化前后的ACC车辆均与前车保持匀速稳定行驶,在2.5 s时,随前车减速而减速,在4 s时,前车驶离本车道,雷达无有效反馈信息,自车进入巡航状态,并逐渐加速至设定车速。在整个仿真过程中,由速度变化曲线可知,优化前后的ACC车辆均可实现较好的速度跟随；但由车距变化曲线可知在车辆减速行驶时,在保证安全的前提下,优化后的跟车距离稍小于优化前,在一定程度上提高了道路通行率；由加速度变化曲线可知,优化后的ACC车辆的加速度峰值较小于未优化车辆,且曲线更为平缓,舒适性更好。

4.2.3 前车加速

设置仿真场景如下：起初前后两车均以30 km/h的速度稳定行驶,车距分别为优化前后安全距离模型计算所得。在1.5 s时,前车以2 m/s2的加速度加速至90 km/h,自车初始设定车速为95 km/h。仿真结果如图13所示。

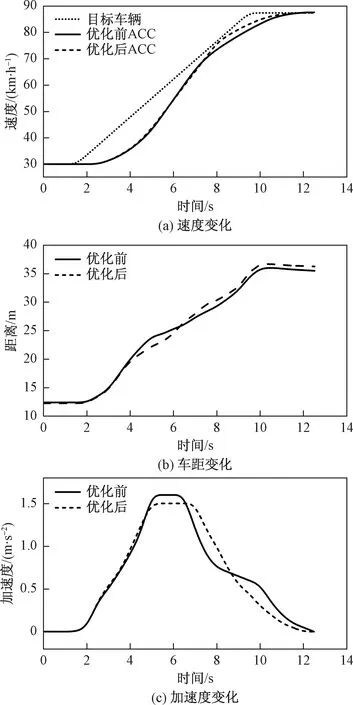
图13 前车加速工况仿真结果

由仿真结果可知,优化前后的ACC车辆均可在速度设定范围内实现对前车的速度跟随,最终与前车保持匀速行驶。由速度变化曲线可知,优化后的ACC车辆速度响应更快,较早达到期望车速；由车距变化曲线可知,优化后的ACC车辆在整个加速过程中,跟车距离随着行驶工况的变化而变化,低速跟车时,保持较小安全距离,以提高道路通行率,高速跟车时,保持较大安全距离,以避免安全事故发生；由加速度变化曲线可知,优化后的ACC车辆加速度峰值较低,但峰值持续时间较长,使得自车具有较好的速度跟随,且峰值过后加速度波动更为平缓,使得驾驶员具有更好的驾驶体验。

4.2.4 前车减速

设置仿真场景如下：起初ACC车辆以50 km/h的设定速度接近前车,而前车则以30 km/h的速度低速行驶,两车相距40 m。在两车速度相等时,前车开始以-2 m/s2的减速度减速至停车。仿真结果如图14所示。

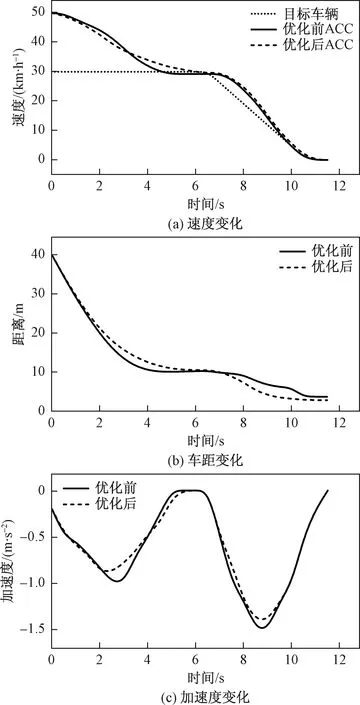
图14 前车减速工况仿真结果

由仿真结果可知,优化前后的ACC车辆均可与前车在保持安全行驶的前提下,实现自车的减速行驶直至安全停车。由速度与加速度变化曲线可知在整个仿真过程中,优化后的ACC车辆在识别到前方目标车辆后,由于安全距离模型的原因,初始速度下降速率相比优化前更大,能够及时避免事故发生,在前后两车速度差值较小后,能够以较小减速度减速至目标车速,在一定程度上保证了驾乘人员的乘坐体验感；由车距变化曲线可知,在整个仿真过程中,优化后的ACC车辆在减速过程中,可以根据行驶工况的变化而动态调整跟车间距,同时满足了驾驶安全性与道路利用率的要求。

5 结论

(1)针对目前自适应巡航系统未考虑车辆驾驶状态实时变化的问题,引入神经网络对车辆驾驶工况分析识别,与现有安全距离模型相结合,完成对该模型的动态优化,建立了一种适应驾驶工况变化的自适应安全距离模型。

(2)通过CarSim与Simulink联合仿真,分别验证了ACC跟车模式下的前车加速、前车减速、前车切入、前车切出工况下的跟车效果,结果表明：基于驾驶工况识别的安全距离模型可以更好地调节跟车安全距离,在保证安全的前提下,该系统可以更好地满足驾驶舒适性要求,同时提高了道路车辆通行率,增加了驾驶员对ACC系统的信任与认可。