无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算

龚凯，向俊，刘林芽，周钦悦，杨海明，吴宝游

无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算

龚凯1，向俊2，刘林芽1，周钦悦1，杨海明2，吴宝游3

(1. 华东交通大学铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；2. 中南大学 土木工程学院，湖南 长沙 410075；3. 中铁电气化局集团有限公司，北京 100036）

为研究无缝线路钢轨鼓胀引起的脱轨规律，以“单波形”钢轨鼓胀为例，建立无缝线路钢轨鼓胀状态下货物列车-轨道系统空间振动计算模型；按照列车脱轨能量随机分析方法，提出无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算方法，计算脱轨全过程，分析鼓胀状态对轮轨几何接触状态和相对位置的影响。研究结果表明：鼓胀波长一定时脱轨系数和轮重减载率随鼓胀幅值增大而增大，鼓胀幅值一定时脱轨系数和轮重减载率随鼓胀波长减小而增大，但脱轨系数和轮重减载率对脱轨缺乏控制作用；转向架与钢轨横向相对位移随鼓胀波长的减小或幅值的增大而增大，得到考虑工况下的最大值为72.6 mm。上述结果可为研发具有实时判别脱轨功能的检测装置提供基础数据。

铁道工程；无缝线路钢轨鼓胀；脱轨全过程；车轮脱轨检测装置

无缝线路因钢轨连接接头少、钢轨平顺性好，轨道结构维修费用低等特点，在高速、重载线路上大量铺设。众所周知，轨道结构常年暴露在自然环境中，受温度影响显著，尤其是在烈日高照下，钢轨内部产生的温度应力使得在钢轨薄弱部分出现钢轨鼓胀现象，严重时甚至发生胀轨跑道。国内外因钢轨鼓胀引起的列车脱轨事故仍时有报道，如2002年美国由弗罗里达州开出的一趟列车因钢轨鼓胀而发生脱轨[1]、2016年由台东开往彰化的651次“莒光号”列车因高温引起的钢轨变形而发生脱轨[2]。在列车运行安全事故中，列车脱轨给人们带来了严重的损失，为预防钢轨鼓胀引起的列车脱轨，国内外学者针对这一问题开展了一些研究[3-12]。Masayuki[3]调查了轨道横向不平顺对两轴列车行车安全的影响，提出对轨道横向不平顺应加强检测与修复；Cheli等[4]采用数值仿真及结合试验研究了钢轨缺陷对城轨电车行车安全的影响；Steenbergen 等[5]探讨了钢轨焊接接头不平顺对列车行车中的轮轨相互作用力的影响；Ishida等[6]研究了钢轨垂向周期性不平顺对车辆脱轨安全性的影响，提出了一种新的脱轨评价准则；Mohammadzadeh等[7-9]系统研究了轨道不平顺对车辆动态响应的影响；XIAO等[10-11]研究了钢轨鼓胀对高速列车行车安全的影响，并基于车轮抬升量、脱轨系数和轮重减载率等安全性指标建立了脱轨安全域准则。实际上，要预防无缝线路钢轨鼓胀引起的列车脱轨，最理想的预防措施是保证无缝线路的稳定性不使其发生钢轨鼓胀，可是因复杂环境、人为或管理不善等因素使得因钢轨鼓胀引起的列车脱轨事故仍偶有发生，难以完全杜绝。并且，在实际行车中，由于货车车辆数较多，在钢轨鼓胀引起的部分车辆脱轨后，驾驶员未能及时察觉，导致事故扩大，造成无法估量的损失。因此，为最大程度减小无缝线路钢轨鼓胀引起的列车脱轨事故带来的损失，确保列车在脱轨第一时间判别车轮是否脱轨，并采取措施及时停车十分必要。为此，基于列车-轨道系统空间振动计算模型[12]、列车脱轨能量随机分析方法[13]，以“单波形”钢轨鼓胀为例，建立无缝线路钢轨鼓胀状态下货物列车-轨道系统空间振动计算模型，提出无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算方法，计算列车脱轨全过程，分析无缝线路钢轨鼓胀对车轮与钢轨间接触状态的影响，得到车轮脱轨瞬间轮轨相对位置和几何尺寸关系，为研发具有实时判别脱轨功能的检测装置提供基础数据。

1 无缝线路钢轨鼓胀状态下货物列车-轨道系统空间振动计算模型

实践表明，无缝线路钢轨鼓胀后的线形多为“单波形”[14]。钢轨鼓胀前、后的无缝线路模型如图1所示。

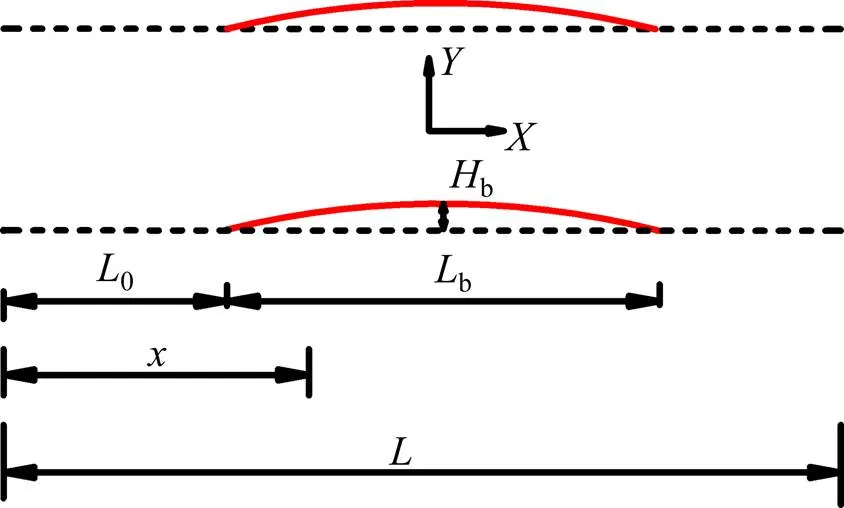
图1 钢轨鼓胀前、后的无缝线路模型

在图1中，黑色虚线为钢轨鼓胀前的线形，红色实线为钢轨鼓胀部分线形，钢轨鼓胀路段设置在轨道长度的中间位置。为钢轨在方向的位置；b为钢轨在方向的鼓胀幅值；b为钢轨鼓胀波长；0为钢轨鼓胀轨道计算起点到钢轨鼓胀起点间的距离。这里，以正弦函数为例模拟钢轨鼓胀线形，如式(1)所示。

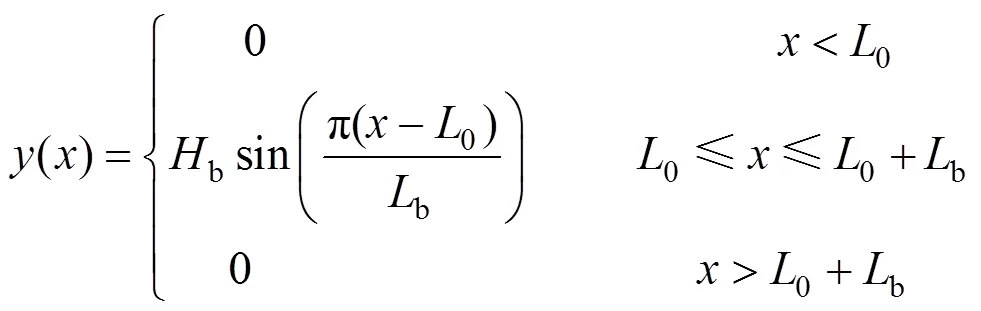
式中：()为钢轨鼓胀的横向位移。

根据式(1)可计算轨道上任意位置处钢轨鼓胀引起的钢轨横向位移，将该位移与轨道初始不平顺叠加来模拟无缝线路钢轨鼓胀后的轨道线路。

基于上述轨道线路，设时刻，一列由1辆机车+辆货车组成的货物列车运行在长度为的轨道上。假定将长度为轨道离散为个轨段单元，针对每个单元建立具有34个自由度的空间振动模型，在模型中，将钢轨和轨枕分别视为弹性点支承Euler梁和放置于道床上的弹性变形体，扣件及道床顶面的弹性均采用线性弹簧与黏滞阻尼器模拟，并且不考虑道床振动。进而可导出第个轨段单元的空间振动势能Tj，并将每一个单元势能进行叠加得到长度范围内轨道空间振动总势能T[12]，如式(2)所示。

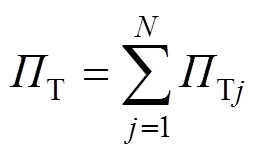
同时，针对车体、前转向架和后转向架均考虑3个平动和3个转动自由度，每个轮对考虑横摆、沉浮2个自由度，形成具有26个自由度机车或车辆模型，进而导出第辆机车或车辆的空间振动势能Vi，并将每一辆机车或车辆的势能叠加得到货物列车空间振动总势能V[12]，如式(3)所示。

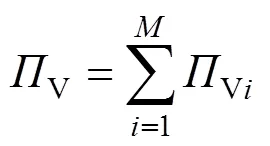
由式(2)和式(3)可得无缝线路钢轨鼓胀状态下货物列车-轨道系统空间振动总势能，如式(4) 所示：

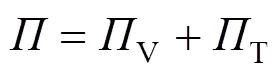
为实现列车脱轨全过程计算，本文取消传统的轮轨“密贴”假定，采用轮轨位移衔接条件[13]作为列车与轨道系统间的纽带并满足轮轨“游间”要求，轮轨位移衔接条件如式(5)～式(6)所示：

w=t+iorΔwt(5)

w=t+iorΔwt(6)

式中：w，w分别为车轮横向和竖向位移；t，t分别为钢轨横向和竖向位移；ior，ior分别为钢轨横向、竖向不平顺；Δwt，Δwt分别为车轮与钢轨间的横向和竖向相对位移。

同时，采用弹性系统动力学总势能不变值原理[15]和“对号入座”法则[13]，形成无缝线路钢轨鼓胀状态下系统的矩阵方程如式(7)所示：

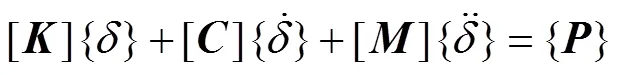
2 无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算方法

研究表明[11, 16-17]，列车低速脱轨表现为爬轨脱轨，而高速脱轨表现为跳轨脱轨。本文研究重点是爬轨脱轨，仍基于文献[13]提出的脱轨机理开展无缝线路钢轨鼓胀引起的货物列车脱轨全过程研究。列车脱轨机理表明[13]，随着输入列车-轨道系统能量不断增大，系统的横向振动逐渐增大，车轮轮缘逐渐爬上钢轨顶部，横向振动状态失去稳定，即列车脱轨。文献[13]表明，采用构架实测(或人工)蛇行波及其标准差p分别作为列车-轨道系统横向振动激振源和输入能量。可是，这里的标准差p是正常行车时测得的，因列车脱轨试验不易实现，脱轨状态下构架蛇行波难以测得，相应的标准差也无法统计。但由压杆失稳临界荷载计算方法可知，通过增大荷载，可试算得到压杆失稳临界状态时临界荷载，这一荷载是使压杆发生失稳的输入能量，比压杆处于失稳临界状态前的任一输入能量都大。同理，使列车发生脱轨的构架蛇行波标准差p1大于列车未脱轨时的构架蛇行波标准差p，比p1更大的系统输入能量不存在，因为列车已经脱轨。为此，提出无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算方法如下：

1) 基于第1节中无缝线路钢轨鼓胀状态下货物列车-轨道系统空间振动计算模型，将某一钢轨鼓胀时“单波形”线形的波长和幅值输入模型。

2) 以实测、统计得到的标准差p为基础，假定一个比p更大的标准差p1，采用Monte-Carlo法随机模拟出一条构架蛇行波输入步骤(1)中的模型，每计算一个时刻的系统振动响应，就按照车轮脱轨几何准则[13]判断该时刻车轮悬浮量是否达到25 mm，若达到，则判定列车脱轨，计算停止；若未达到，则继续计算，直到满足上述要求为止。此时，得到的系统空间振动响应反映了无缝线路钢轨鼓胀引起的货物列车脱轨全过程。

3) 若步骤2)仍未能判定列车脱轨，则通过减小“单波形”线形波长或增大幅值，重复步骤1)～2)，直到实现无缝线路钢轨鼓胀引起的货物列车脱轨全过程计算为止。

3 计算实例与分析

研究及实践表明[13]，我国自提速以来空载货车发生脱轨概率较大。本节以1辆DF4型机车+16辆C62型空载敞车为例，计算车速=80 km/h时列车在300 m有砟轨道上的脱轨全过程。有砟轨道结构由60 kg/m钢轨、II型混凝土轨枕及碎石道砟组成，轨枕间距为0.543 5 m。根据前述模型及计算方法，参考文献[11]中采用的钢轨鼓胀波长和幅值，分别计算钢轨鼓胀波长分别为20，30，40和50 m，幅值分别为40，60，80和100 mm时货物列车脱轨全过程，得到脱轨车轮在脱轨瞬间的悬浮量Δz，脱轨车辆i，脱轨车轮在脱轨瞬间的脱轨系数及轮重减载率脱轨车轮对应的转向架与钢轨横向相对位移Δ等动力响应，计算结果见表1所示。

由表1可知，因无缝线路钢轨鼓胀引起的脱轨车辆i为第1车(机车)或第2车，均位于列车编组前部；并且，在钢轨鼓胀波长b一定时，随着鼓胀幅值b的增大，钢轨不平顺逐渐急剧，脱轨车辆i由第2车变为第1车(机车)。可见，钢轨鼓胀对列车行车安全具有直接影响。

在表1的计算工况中，当波长b一定时，随着幅值b的增大，车轮脱轨瞬间脱轨系数增大；当幅值b一定时，随着波长b的增大，脱轨系数减小。脱轨系数最大为1.14，最小为0.18，均未超过规范GB5599—85[18]中要求的脱轨系数限值1.2，但车轮发生脱轨。因此，钢轨鼓胀波长及幅值对脱轨系数具有一定的影响，但脱轨系数难以判别车轮是否脱轨。

表1 不同鼓胀波长及幅值条件下货物列车脱轨全过程计算结果

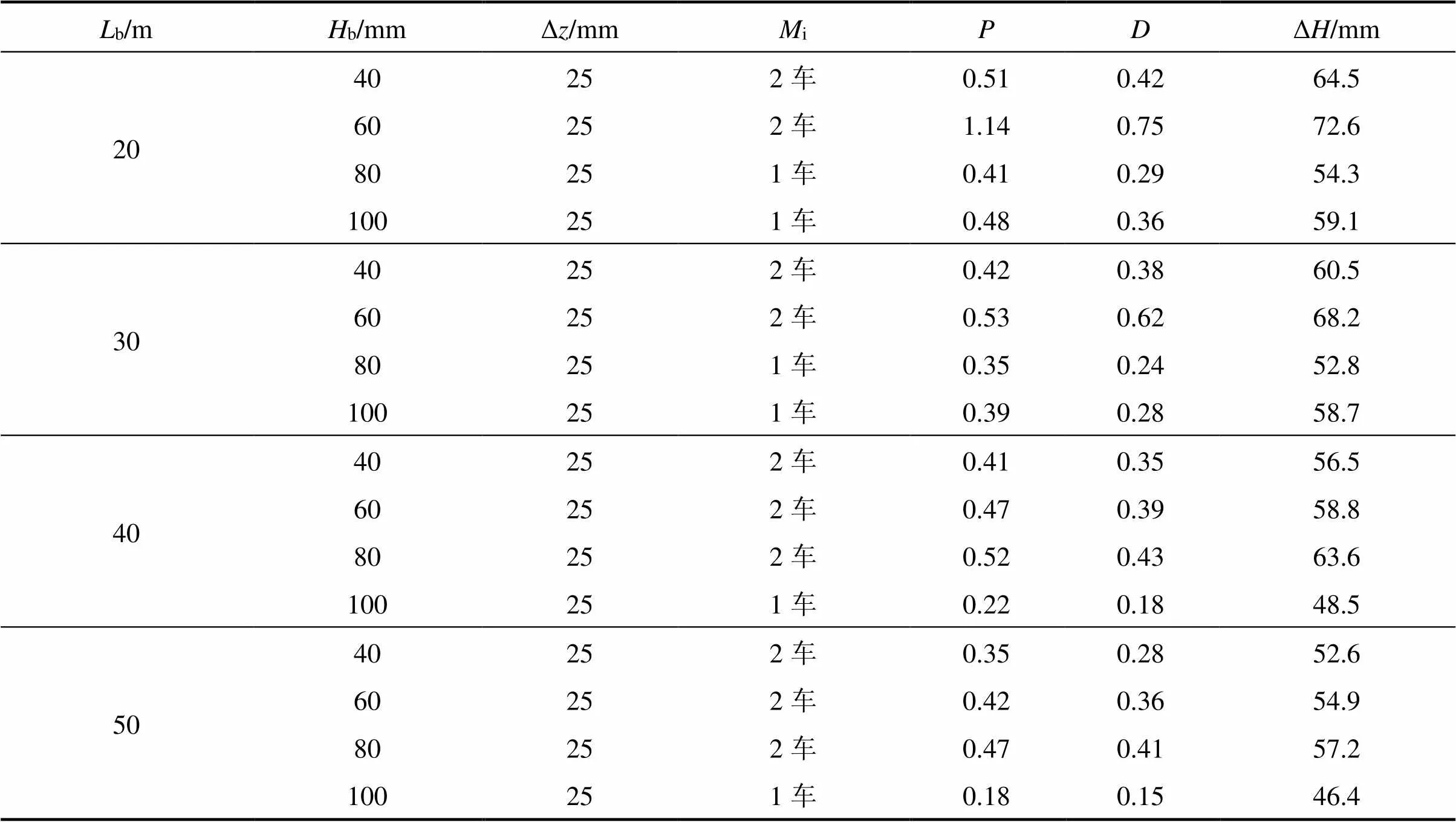
Table 1 Calculation results of the whole derailment process of freight train at different rail bucking wavelength and amplitude

此外，当鼓胀波长b一定时，鼓胀幅值b的增大，车轮在脱轨瞬间的轮重减载率增大；当鼓胀幅值b一定时，鼓胀波长b增大，相应的轮重减载率减小。在表1各工况中，当车轮脱轨时，轮重减载率最大为0.75，超过规范GB5599—85[18]要求的限值0.65，而最小为0.15，未超过限值要求。可见，钢轨鼓胀波长及幅值对轮重减载率也具有一定的影响，但轮重减载率难以在其未超限时判别车轮是否脱轨。

为给研发具有实时判别脱轨功能的检测装置提供基础数据，本文计算了无缝线路钢轨鼓胀状态下车轮脱轨瞬间转向架与钢轨横向相对位移Δ，计算结果如表1所示。由表1可知，当波长b一定时，机车、车辆在脱轨瞬间脱轨车轮对应的转向架与钢轨横向相对位移Δ随幅值b的增大而增大；而当幅值b一定时，机车、车辆在脱轨瞬间脱轨车轮对应的转向架与钢轨横向相对位移Δ随波长b的减小而增大。可见，在钢轨鼓胀后，随着幅值b的增大及波长b的减小，钢轨逐渐形成较为急剧的不平顺，此时，机车或车辆振动剧烈。此外，因机车质量大于车辆，则机车横摆幅度较小，机车脱轨车轮对应转向架与钢轨横向相对位移Δ也比车辆的相应值小。综上所述，在本文考虑的工况中，当钢轨鼓胀波长b为20 m、幅值b为60 mm时，转向架与钢轨横向相对位移Δ最大，为72.6 mm。

为直观分析无缝线路钢轨鼓胀引起的货物列车脱轨全过程，钢轨鼓胀波长b为20 m、幅值b为60 mm时脱轨车轮的车轮悬浮量、脱轨系数、轮重减载率和转向架与钢轨横向相对位移时程曲线如图2～5所示。在该工况下，根据钢轨鼓胀波长及轨道计算长度可得钢轨鼓胀路段设置在距轨道起点140～160 m处。

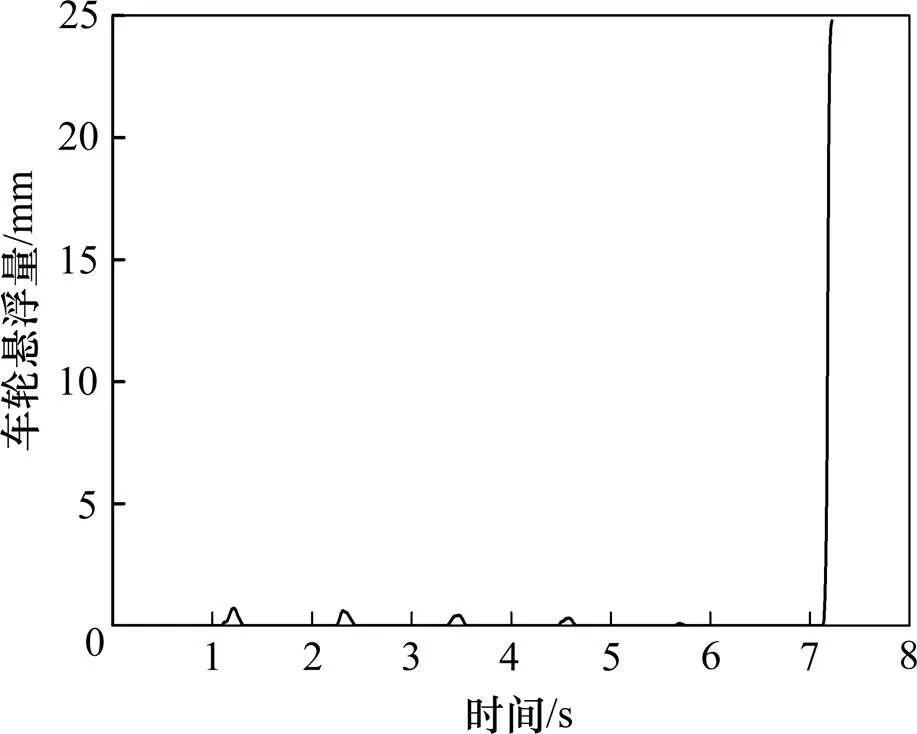
图2 第2车第1轴右轮悬浮量时程曲线

由图2表明，在列车运行至第7 s前，第2车第1轴右轮悬浮量较小，而在第7 s后第2车第1轴右轮悬浮量急剧增大至25 mm，达到车轮脱轨几何准则[13]判定车轮脱轨要求。按照列车运行速度，可得列车在第7 s时已运行至80/3.6×7.0=155.6 m处，此时，列车已进入钢轨鼓胀路段。可见，钢轨鼓胀对车轮悬浮量影响明显，对行车安全具有直接影响。

此外，由图3～4表明，车轮脱轨前脱轨系数及轮重减载率最大值分别为3.63和0.79(图中的负号表示与坐标方向相反)，均超过规范限值[18]要求，但车轮未脱轨。当车轮脱轨时脱轨系数为1.14，轮重减载率为0.75，脱轨系数虽未超过限值，但接近限值1.2，而轮重减载率超过限值要求。可见，钢轨鼓胀对脱轨系数和轮重减载率均具有影响，但脱轨系数和轮重减载率在其超过规范限值时难以判别车轮是否脱轨。

最后，由图5表明在脱轨瞬间，与第2车第1轴右轮相应的转向架与钢轨横向相对位移增大 明显。

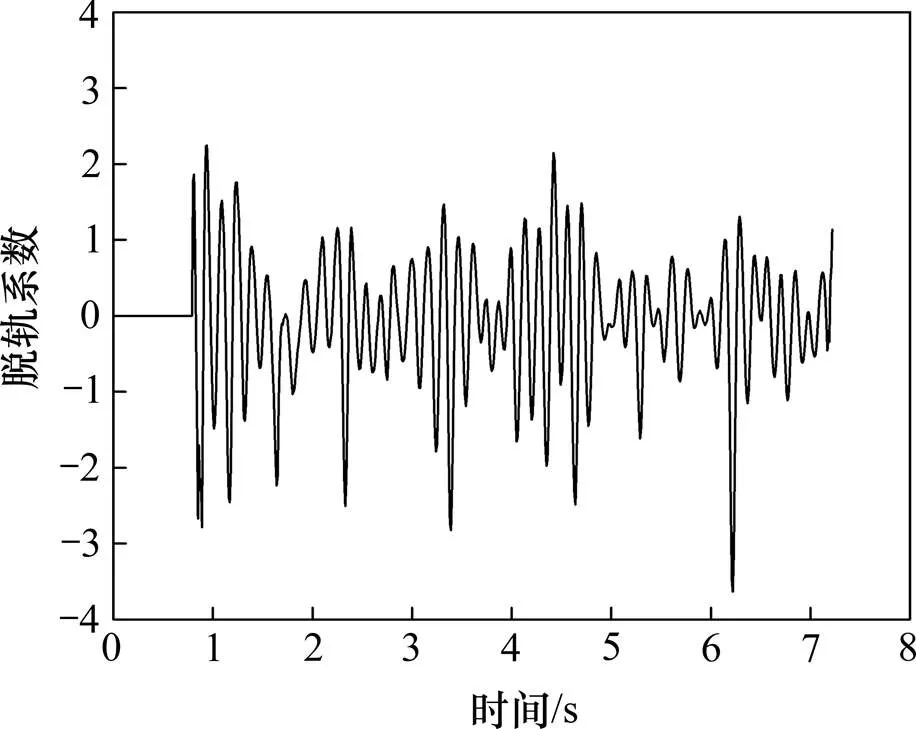
图3 第2车第1轴右轮脱轨系数时程曲线

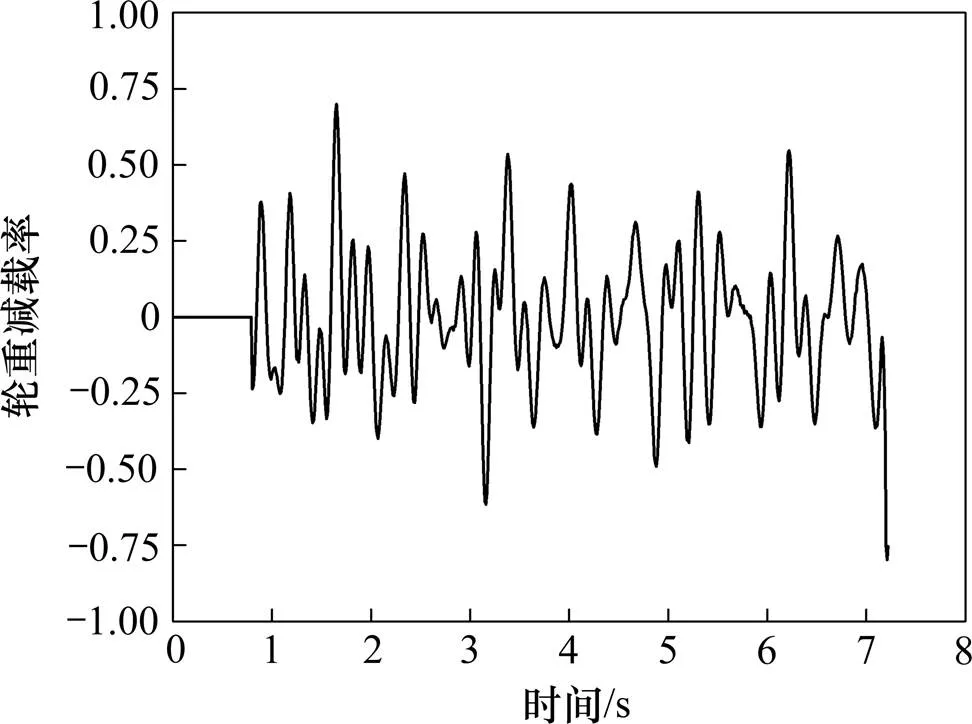
图4 第2车第1轴右轮轮重减载率时程曲线

图5 第2车前转向架与右侧钢轨横向相对位移时程曲线

4 结论

1) 钢轨鼓胀波长及幅值对脱轨系数、轮重减载率均有影响，但脱轨系数、轮重减载率在其超过规范限值时难以判别钢轨鼓胀状态下车轮是否脱轨。

2) 转向架与钢轨横向相对位移随鼓胀幅值的增大及波长的减小而增大明显。

3) 通过计算得到了波长20 m，幅值60 mm时转向架与钢轨横向相对位移为72.6 mm，此为本文分析结果中的最大值。该值反映了轮轨在脱轨瞬间的相对位置，并且考虑到检测装置不易安装在车轮表面，故将其安装在转向架上，以转向架的动态行为作为阀值，既克服检测装置不易安装，也起到了第一时间判别车轮脱轨的作用，进而为研发具有实时判别脱轨功能的检测装置提供参考。

4) 本文研究的是列车低速时钢轨鼓胀引起的车轮爬轨脱轨，对于列车高速时钢轨鼓胀引起的车轮跳轨脱轨研究将在后续文章中报道。

[1] Brabie D. On the influence of rail vehicle parameters on the derailment process and its consequences[D]. Stockholm: KTH, Sweden, 2005.

[2] 俞菁. 台湾发生火车脱轨事件疑因高温致铁轨变形[EB/OL]. 2016-06-06.http://news.youth.cn/gn/201606/t 20160606_8087735.htm.YU Jing. Train derailment in Taiwan is suspected to caused by railway track deformation due to high temperatures[EB/OL]. 2016-06-06.http://news.youth.cn/ gn/201606/t20160606_8087735.htm.

[3] Masayuki I. A study of track maintenance for the derailment due to the interaction between track and vehicle[J]. Japanese National Railway Technical Research Institute Quarterly Reports, 1978, 19(1): 1-6.

[4] Cheli F, Corradi R, Diana G, et al. Effect of track geometrical defects on running safety of tramcar vehicles [J]. Vehicle System Dynamics, 2006, 44(Suppl 1): 302- 312.

[5] Steenbergen M, Esveld C. Relation between the geometry of rail welds and the dynamic wheel-rail response: numerical simulations for measured welds[J]. Proceeding of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2006, 220(4): 409- 423.

[6] Ishida H, Matsuo M, Fujioka T. Safety assessment method of railway vehicle under oscillatory wheel load fluctuation[J]. Journal of Environment and Engineering, 2007, 2(2): 407-418.

[7] Mohammadzadeh S, Sangtarashha M, Molatefi H. A novel method to estimate derailment probability due to track geometric irregularities using reliability techniques and advanced simulation methods[J]. Archive of Applied Mechanics, 2011, 81(11): 1621-1637.

[8] Suarez B, Felez J, Antonio Lozano J, et al. Influence of the track quality and the properties of the wheel-rail rolling contact on vehicle dynamics[J]. Vehicle System Dynamics, 2013, 51(2): 301-320.

[9] Choi I Um J H, Lee J S, et al. The influence of track irregularities on the running behavior of high-speed trains[J]. Proceeding of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2013, 227(1): 94-102.

[10] XIAO Xinbiao, JIN Xuesong, WEN Zefeng. Effect of tangent track buckle on vehicle derailment[J]. Multibody System Dynamics, 2011, 25(1): 1-41.

[11] 肖新标. 复杂环境状态下高速列车脱轨机理研究[D]. 成都: 西南交通大学, 2013. XIAO Xinbiao. Study on high-speed train derailment mechanism in severe environment[D]. Chengdu: Southwest Jiaotong University, 2013.

[12] XIANG Jun, LI Dejian, ZENG Qingyuan. Simulation of spatially coupling dynamic response of train track time variant system[J]. Journal of Central South University of Technology, 2003, 10(3): 226-230.

[13] 曾庆元, 向俊, 周志辉, 等. 列车脱轨分析理论与应用[M]. 长沙: 中南大学出版社, 2006: 204-276. ZENG Qingyuan, XIANG Jun, ZHOU Zhihui, et al. Analysis theory and application of train derailment[M]. Changsha: Central South University Press, 2006: 204- 276.

[14] 陈秀方. 轨道工程[M]. 北京: 中国建筑工业出版社, 2017: 244-246. CHEN Xiufang. Track engineering[M]. Beijing: China Architecture & Building Press, 2017: 244-246.

[15] ZENG Qingyuan, LOU Ping, XIANG Jun. The principle of total potential energy with stationary value in elastic system dynamics and its application to the analysis of vibration and dynamic stability[J]. Journal of Huangzhong University of Science & Technology (Urban Science Edition), 2002, 19(1): 7-14.

[16] 翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015: 427-434. ZHAI Wanming. Vehicle-track coupled dynamics[M]. 4th ed. Beijing: Science Press, 2015: 427-434.

[17] 陈淮, 杜晓伟, 曾庆元. 车辆脱轨问题的探讨[J]. 郑州工业大学学报, 2010, 21(18): 2192-2195. CHEN Huai, DU Xiaowei, ZENG Qingyuan. Discussion about derailment problem of vehicles[J]. Journal of Zhengzhou University of Technology, 2010, 21(18): 2192-2195.

[18] GB5599—85, 铁道车辆动力学性能评定和试验鉴定规范[S]. GB5599—85, Railway vehicle-sepcification for evaluation the dynamic performance and accreditation test[S].

Calculation of freight train derailment process caused by rail bucking of CWR

GONG Kai1, XIANG Jun2, LIU Linya1, ZHOU Qinyue1, YANG Haiming2, WU Baoyou3

(1. Engineering Research Center of Railway Environmental Vibration and Noise, Ministry of Education, East China Jiaotong University, Nanchang 330013, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China; 3. China Railway Electrification Bureau Group Co., Ltd., Beijing 100036, China)

In order to study freight train derailment law caused by the rail bucking of CWR, the spatial vibration calculation model for the freight train-track system under the rail bucking of CWR was established by taking the “single waveform” rail bucking as an example. According to the random energy analysis method of train derailment, a calculation method for the whole derailment process of freight train caused by the rail bucking of CWR was proposed. The train derailment processes were calculated and the effects of the rail bucking condition on the wheel-rail geometric contact state and relative position were analyzed. Results show that the derailment coefficient and wheel load reduction ratio increase with the increase of bucking amplitude when the wavelength of rail bucking is fixed. Meanwhile, the derailment coefficient and wheel load reduction ratio increase with the decrease of bucking wavelength when the bucking amplitude is fixed. However, the derailment coefficient andwheel load reduction ratio lack control function for the derailment caused by the rail bucking. The lateral relative displacement between bogie and rail increase with the decrease of bucking wavelength or the increase of bucking amplitude of the rail, and the maximum relative displacement of the study case is 72.6 mm. The above results can provide the basic data for the development of a detection device with a real-time derailment detection function.

railway engineering; rail bucking of CWR; whole process of derailment; wheel derailment detection device

U213.2

A

1672 - 7029(2020)11 - 2767 - 07

10.19713/j.cnki.43-1423/u.T20191174

2019-12-26

国家自然科学基金委员会与神华集团有限公司联合资助项目(U1261113)；国家自然科学基金资助项目(51578238，52068028)；江西省优秀科技创新团队建设计划项目(20152BCB24007)；华东交通大学科研启动基金资助项目(10012003416034)；赣教高字[2018]江西省教育厅科学技术项目(GJJ170392)

向俊(1968-)，男，湖南溆浦人，教授，博士，从事列车脱轨控制、列车-轨道(桥梁)系统振动及铁路轨道结构等研究；E-mail：jxiang@csu.edu.cn

(编辑 涂鹏)