上海黏土固结特性及其各向异性的试验研究

倪静，朱丛薇，韩玉琪，郝港来

上海黏土固结特性及其各向异性的试验研究

倪静1，朱丛薇1，韩玉琪2，郝港来1

(1. 上海理工大学 环境与建筑学院，上海 200093；2. 上海申元岩土工程有限公司，上海 200021)

为研究上海黏土在固结过程中固结系数、体积压缩系数及渗透系数的变化规律及各向异性，对竖直向和水平向原状上海黏土土样进行逐级加载固结试验。试验结果表明：在固结过程中，固结系数与固结应力关系呈凹型曲线，水平向土样的固结系数略大于竖直向土样，且水平向土样固结系数最小值对应的固结应力小于竖直向土样；在自然沉积过程中，水平向片状结构土颗粒团聚成的絮状物沉淀逐渐形成上海黏土，因而水平向土样的孔隙比比竖直向略大，导致水平向渗透系数比竖直向大，但是由于竖直向与水平向土样在固结过程中受轴力方向与片状结构土颗粒所成角度不同，水平向土样压缩性比竖直向土样小。研究结果不仅完善了上海黏土各向异性的固结力学特性，也可为上海黏土地区的工程施工提供参考。

上海黏土；固结特性；各向异性；固结系数；压缩系数；渗透系数

随着城市地铁轨道交通、机场、高速公路、高层以及超高层建筑基坑、市政工程、水利设施、海防及堤坝等大量工程在软土地基上建造施工，了解和掌握软土地基的物理力学特性，特别是固结特性成为这些工程建设安全实施的关键。近年来，随着研究的不断深入，土的各向异性固结特性获得了越来越多的关注。土的各向异性是指天然土体在沉积过程中因土颗粒在不同方向的排列不同，而引起的不同方向力学性状不同[1-4]。目前，已有许多国内外学者对黏土的各向异性固结特性(固结系数、渗透系数及体积压缩系数)进行了分析研究。关于固结系数的各向异性，Wong[5]对竖直向及水平向泥炭土土样进行逐级加载固结试验，发现当固结应力小于200 kPa，水平向与竖直向固结系数的比值大于1。Seah等[6]对竖直向及水平向Bangkok 黏土土样进行了恒应变速率固结试验，发现当固结应力从20 kPa增加至500 kPa时，水平向和竖直向固结系数的比值增大。关于渗透系数的各向异性，Chapuis等[7]通过对砂和黏性土进行渗透试验，发现孔隙比越小, 渗透各向异性比越大，并建立了用孔隙比表述的指数型渗透各向异性模型。Adams等[8]基于波士顿蓝黏土渗透各向异性的试验数据，拟合得到用孔隙比表述的线性渗透各向异性模型。O’Kelly[9]通过逐级加载固结试验研究了 11 种软土的渗透特性，发现不同软土水平向与竖直向渗透系数的比值在1到1.7 之间。宋云奇等[10]对竖直向及水平向上海浅部黏土土样进行逐级加载固结试验，发现水平渗透系数略大于竖直渗透系数。徐杰等[11]通过对高岭-蒙脱混合黏土进行渗透试验，发现宏观参数孔隙比不是决定渗透各向异性比的关键，证明了从微观角度探究渗透各向异性的可行性。关于体积压缩系数各向异性的研究不多，加瑞等[12]对水平向与竖直向日本有明黏土进行了恒应变速率固结试验，发现在超固结阶段，水平体积压缩系数明显大于竖向体积压缩系数；在先期固结压力附近，水平体积压缩系数小于竖向体积压缩系数；而正常固结阶段，水平压缩系数与竖向压缩系数基本相等。综上所述，这些研究多集中于固结特性中的单个方面，同时涉及土体固结系数、压缩系数及渗透系数三者各向异性的综合性研究文献还不多[12]。因此，本文作者通过对上海轨道交通15号线古浪路站基坑采集的竖直向及水平向原状土样进行逐级加载固结试验，分析探讨固结系数、压缩系数与渗透系数在固结过程中的变化及其各向异性。由于上海黏土的物理力学特性具有非常明显的地域性，因此，研究总结上海地区的软黏土固结特性对于指导该地区的工程建设具有重要的现实意义。

1 试验仪器与试样制备

1.1 试验仪器

本试验仪器为YS-2型压缩仪，该仪器采用常规杠杆式压力机，具有杠杆刚度大的特点(铸造材质为高强度铝合金)。该仪器具有1:10及1:12 共2种加压比，最小加载值为12.5 kPa，最大加载值为1 600 kPa，可以满足本试验对荷载等级的需求。

1.2 试样制备

本试验采用原状土样，取自上海轨道交通15号线古浪路站基坑，该工程勘察时一共取50个勘探点，本试验所取原状土样位于孔号S25XJ23附近，该区域的工程地质剖面图如图1所示。

取样时，用直径为6.18 cm，高度为2 cm内壁涂凡士林的环刀在土层上切取土样。环刀水平放置切取竖直向土样，如图2(a)所示；将环刀旋转90°，竖直放置切取水平向土样，如图2(b)所示。

按《土工试验方法标准》(GB/T50123—2019)[13]要求，测定土样的基本物理性质指标如表1所示。试验前，将土样置于叠加器中压紧，放入真空饱和缸中，进行抽气饱和，24 h后将土样从饱和缸中取出，准备进行固结试验。

2 试验方案设计

本文利用固结仪对不同埋深、不同方向(水平向和竖直向)的原状土样，进行常规逐级加载固结试验，试验方案如表2所示。土样按如下方式命名：第1个字母代表土样方向，V为竖向土样、H为水平向土样；第2个数字代表土样深度，1为第1层8.9 m，2为第2层14.8 m，3为第3层19.6 m。本试验逐级加载的加载比，除了第2和3层土样增加了中间值3/2及4/3以外，其余均为2。

图1 取样区域的工程地质剖面图

图2 现场取样图

表1 试样物理性质指标

试验过程中，按《土工试验方法标准》(GB/ T50123—2019)[13]规定记录下仪表盘的土样变形量数据，并每隔24 h施加下一级荷载。某一级荷载作用下的固结系数获取方式如下：采用时间平方根法及时间对数法分别计算固结系数，并反复迭代调整结果，使两者互相逼近，取平均值作为固结系数。体积压缩系数可通过下式获得：

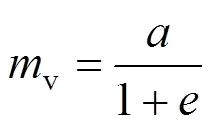
为上级荷载土样固结稳定后的孔隙比。

由固结系数的定义可推求渗透系数的计算 公式：

式中：w为水的重度；v为某级荷载下土样的固结系数。

表2 逐级加载固结试验方案

3 试验结果与分析

3.1 固结系数

图3为逐级加载固结过程中，上海黏土竖直向及水平向土样的固结系数随固结应力的变化曲线。可以看出，竖直向与水平向土样固结系数具有相似的变化规律，即固结系数先减小后增大；并且随着取土深度的增加，土样固结系数减小且固结系数最小值对应的固结应力增大。以水平向土样为例，当取土深度为8.9 m时，随着固结应力的增大固结系数先减小，在50 kPa固结应力附近达到最小值后增大；当取土深度为14.8 m及19.6 m时，固结系数最小值对应的固结应力分别为100 kPa及200 kPa。固结系数的这种变化规律可能与先期固结应力及当前固结应力之间的相对大小变化有关。由于原状土样在取出前，上覆土层的自身重力及先前可能存在建筑物等影响，土样存在先期固结应力；并且随着取土深度的增加，上覆土层厚度增加，先期固结应力越大。在加载初期，当前固结应力小于先期固结应力，固结系数随着固结应力的增大而减小；当当前固结应力等于先期固结应力时，固结系数取得最小值；当前固结应力大于先期固结应力时，固结系数随着固结应力的增大而增大。描述固结系数在某级固结应力附近出现极值的文献见[14-15]，其中文献[15]得到的结论与本文类似，即固结系数存在最小值(固结系数与固结应力关系呈凹型曲线)；文献[14]得到的结论与本文相反，即固结系数存在最大值(固结系数与固结应力关系呈凸型曲线)。

由固结系数的定义可知，凹型曲线与凸型曲线的出现与固结过程中渗透系数与体积压缩系数的相对变化有关：若1) 当先期固结应力大于当前固结应力时，+1/vi+1＜k/vi；当先期固结应力等于固结应力时，+1/vi+1=kvi；当先期固结应力小于当前固结应力时，+1/vi+1＞k/vi，则固结系数与固结应力关系呈凹型曲线。2) 反之，则呈凸型曲线。

图3 不同取土深度处原状土样固结系数-固结应力曲线

此外，对比图3不同深度处水平向土样的固结系数，发现存在试验曲线的交叉现象，原因如下：由前述可知，本文固结系数与固结应力关系呈凹型曲线，并且随着取土深度的增加，土样固结系数最小值对应的固结应力增大。以取土深度为14.8 m的土样为例，固结系数在100 kPa固结应力附近达到最小值后增大，而取土深度为19.6 m的土样固结系数在200 kPa固结应力附近达到最小值后增大。因此，在固结应力由100 kPa 增长到200 kPa的过程中，取土深度为14.8 m的土样固结系数开始增大，而取土深度为19.6 m的土样固结系数仍在减小，从而出现了2条试验曲线的交叉现象。

对比相同取土深度的竖直向及水平向土样的固结系数发现，水平向土样的固结系数略大于竖直向土样的固结系数。此外，对于取自同一深度处的竖直向及水平向土样(除19.6 m外)，固结系数与固结应力关系凹型曲线极值点对应的固结应力值并不相同，竖直向土样大于水平向土样。例如，当取土深度为8.9 m时，竖直向土样固结系数最小值对应的固结应力为100 kPa，而水平向土样为50 kPa；当取土深度为14.8 m时，竖直向及水平向土样固结系数最小值对应固结应力分别为200 kPa及100 kPa。联系之前提到的极值点出现在先期固结应力附近，说明竖直向土样的先期固结应力大于水平向土样。对于某一取土深度，竖直向土样经历的最大轴向(加载方向)有效应力为，而水平向土样经历的最大轴向(加载方向)有效应力为0，因此水平向土样极值点较竖直向土样出现得早。

3.2 压缩系数

图4为上海黏土随取土深度变化的压缩曲线，可以看出，孔隙比的变化量随取土深度增加而减小。取土深度为8.9 m土样(竖直向及水平向)的孔隙比变化量都是最大的，取土深度为19.6 m的土样最小。此外，对比图4不同深度处水平向土样的压缩曲线，发现取土深度为8.9 m和19.6 m的试验曲线存在交叉现象，原因如下：由前述可知，土样的取土深度越大，先期固结应力就越大，因而取土深度较大的土样具有较大的压实程度，导致在再压缩阶段取土深度为19.6 m土样的孔隙比变化量较小。此外，取土深度为8.9 m的土样属于④1灰色淤泥质黏土，具有高压缩性，而取土深度为19.6 m的土样属于⑤3-1灰色粉质黏土，具有中～高压缩性(小于前者)。综上所述，以取土深度为8.9 m的土样为例，初始孔隙比为1.213，最终孔隙比为0.714，压缩过程中孔隙比的变化量为0.499。当取土深度为19.6 m时，土样的初始孔隙比为1.15，最终孔隙比为0.833，压缩过程中孔隙比的变化量为0.317。所以，2条曲线存在交叉现象。

根据图4数据，运用式(1)计算各固结应力下的体积压缩系数，如图5所示。可知，体积压缩系数随着固结应力的增大而减小。除取土深度为8.9 m的竖直向土样，其余土样的体积压缩系数曲线差别不大。当固结应力大于400 kPa，所有土样的体积压缩系数趋于一致。

图4 不同取土深度处原状土样孔隙比-固结应力对数关系曲线

图5 不同取土深度处原状土样体积压缩系数-应力关系曲线

此外，通过对比图4中不同方向土样的压缩曲线，可以发现水平向土样的孔隙比比竖直向土样的孔隙比略大。这可能是因为在自然沉积环境中，上海黏土由水平向片状结构土颗粒团聚成的絮状物形成[10]，因而水平向的孔隙比较竖直向的孔隙比略大，如图6所示。另一方面，竖直向土样的体积压缩系在300 kPa之前略大于水平向土样。这是因为在200～300 kPa之前，原状土样具有较强的结构性，竖直向土样所受固结应力方向与水平向片状土颗粒所成角度较大，较易使土颗粒发生错动、体积压缩；水平向土样所受固结应力方向与水平向片状土颗粒所成角度较小，较难使土颗粒发生错动，此时土颗粒本身在颗粒轴向受力发生压缩变形，但土颗粒本身的压缩变形很小，不及全部土体压缩变形的1/400，因此水平向土样的压缩性不及竖直向土样。当固结应力超过300 kPa后，土体结构性在较大的应力水平下逐渐被破坏，故不同方向土样的压缩性逐渐趋近。

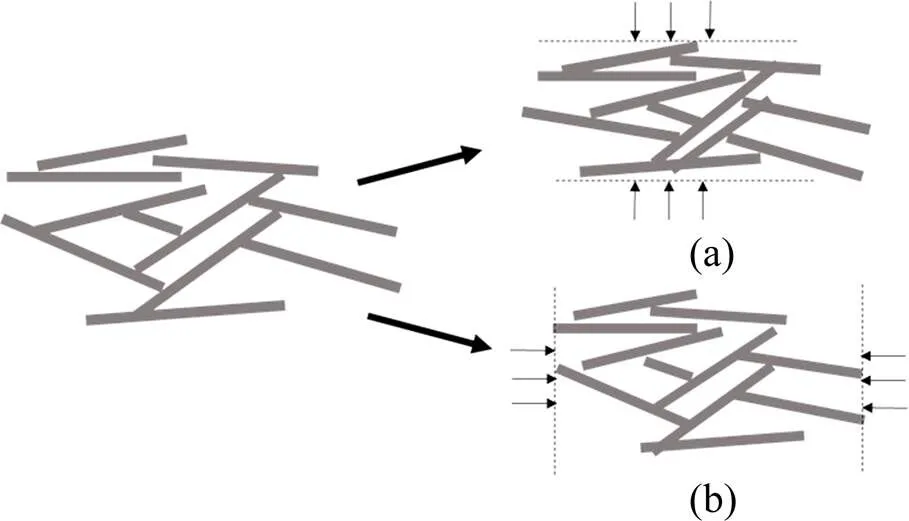
图6 黏土颗粒受力示意图

3.3 渗透系数

图7为原状土样渗透系数随应力变化的曲线：随着固结应力的增加，孔隙水排出、孔隙体积减小，导致渗透系数减小。对比图7不同深度处水平向土样的渗透系数-应力关系曲线，发现存在试验曲线的交叉现象，原因如下：由前所述，取土深度为8.9 m的土样属于④1灰色淤泥质黏土，其压缩性大于取土深度为19.6 m的土样(属于⑤3-1灰色粉质黏土)。因而在固结过程中，取土深度为8.9 m的土样孔隙比变化较大，导致与孔隙比有关的渗透系数也变化较大，因此出现试验曲线的交叉现象。另外，通过对比可知，水平向土样渗透系数的数值在1.20×10-9m/s～9.20×10-9m/s之间，比竖直向土样渗透系数略大(竖直向为8.90×10-10m/s～5.30× 10-9m/s)。原因在之前已有提及，即上海黏土的自然沉积过程引起了各向异性。随着土体沉积，土颗粒在竖直向和水平向形成了不同的排列接触形式，大部分片状黏土颗粒趋向于水平定向排列，相比于竖直向，水平向具有更大的孔隙比(见图6)，水更容易从水平向渗流，因而水平向的渗透系数大于竖直向的渗透系数。

图8为原状土样孔隙比与渗透系数在双对数坐标中的关系图，可知不同取土深度及不同取土方向得到的原状土样的数据点较集中。对试验所得渗透系数的对数随孔隙比变化的数据进行直线拟合，得到相关性系数R为0.95，可知二者基本呈线性 关系。

图7 不同取土深度处原状土样渗透系数-应力关系曲线

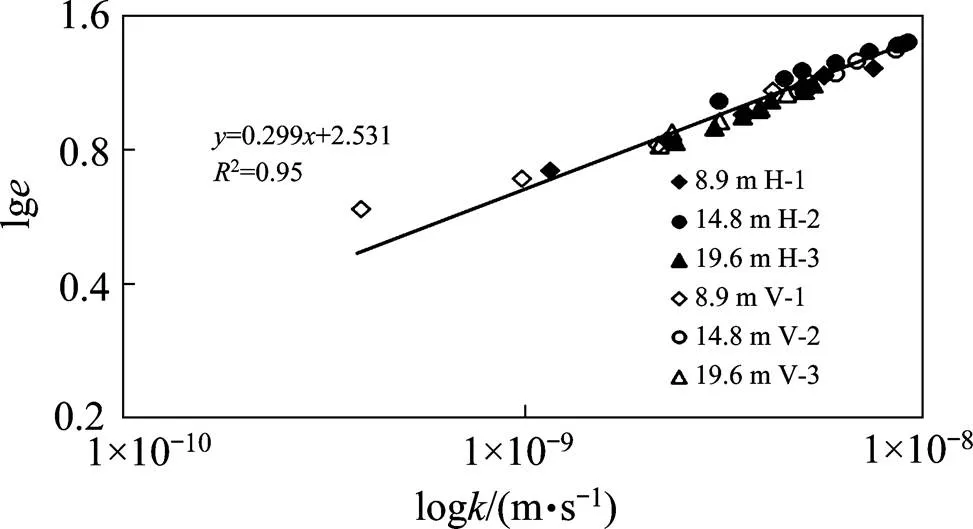
图8 渗透系数对数-孔隙比对数关系曲线

4 结论

1) 上海黏土竖直向与水平向土样固结系数具有相似的变化规律，即固结系数先减小后增大，固结系数与固结应力曲线呈凹型；并且随着取土深度增加，固结系数最小值对应的固结应力也相应 增大。

2) 上海黏土的固结系数存在各向异性，即水平向固结系数略大于竖直向固结系数。此外，水平向土样固结系数-固结应力凹型曲线拐点对应的固结应力小于竖直向土样。

3)上海黏土由水平向片状结构土颗粒团聚成的絮状物形成，因而水平向土样的孔隙比较竖直向的孔隙比略大。但是，水平向土样的压缩性却小于竖直向土样，这是因为竖直向土样所受的应力方向与水平向片状土颗粒所成角度较大，易使土颗粒发生错动，体积压缩；水平向土样所受应力方向与水平向片状土颗粒所成角度小，土颗粒较难发生错动，且土颗粒本身较难发生压缩，所以水平压缩性较竖向压缩性小。

4) 上海黏土的渗透系数随着固结应力增大而减小，并且水平渗透系数大于竖直向渗透系数。不同取土深度及不同取土方向土样的孔隙比与渗透系数在双对数坐标中呈现良好的线性关系。

[1] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2016. LI Guangxin. Advanced soil mechanics[M]. Beijing: Qinghua University Press, 2016.

[2] Mitchell J K, Soga K. Fundamentals of soil behavior[M]. Wiley, New York, USA, 2005.

[3] 龚晓南. 高等土力学[M]. 杭州: 浙江大学出版社, 1996. GONG Xiaonan. Advanced soil mechanics[M]. Hangzhou: Zhejiang University Press, 1996.

[4] 钱家欢, 殷宗泽. 土工原理与计算[M]. 2版. 北京: 中国水利水电出版社, 1996. QIAN Jiahuan, YIN Zongzhe. The principle of soil engineering and calculation[M]. 2nd ed. Beijing: China Water & Power Press, 1996.

[5] Wong L S. Laboratory evaluation of horizontal coefficient of consolidation, Ch of fibrous peat soil[D]. Malaysia: University of Malaya, 2005.

[6] Seah T H, Juirnarongrit T. Constant rate of strain consolidation with radial drainage[J]. Geotechnical Testing Journal, 2003, 26(4): 1-12.

[7] Chapuis R P, Gill D E. Hydraulic anisotropy of homogeneous soils and rocks: Influence of the densification process[J]. Bulletin of Engineering Geology & the Environment, 1989, 39(1): 75-86.

[8] Adams A L, Germaine J T, Flemings P B, et al. Stress induced permeability anisotropy of Resedimented Boston Blue Clay[J]. Water Resources Research, 2013, 49(10): 6561-6571.

[9] O’Kelly B C. Compression and consolidation anisotropy of some soft soils[J]. Geotechnical and Geological Engineering, 2006, 24(6): 1715-1728.

[10] 宋云奇, 武朝军, 叶冠林. 上海浅部黏土渗透系数及其各向异性[J]. 岩土力学, 2018, 39(6): 2139-2144. SONG Yunqi, WU Chaojun, YE Guanling. Permeability and anisotropy of upper Shanghai clays[J]. Rock and Soil Mechanics, 2018, 39(6): 2139-2144.

[11] 徐杰, 周建, 罗凌晖, 等. 高岭-蒙脱混合黏土渗透各向异性模型研究[J]. 岩土力学, 2020, 41(2): 1-9. XU Jie, ZHOU Jian, LUO Linghui, et al. Study on permeability anisotropy model of Kaolin- Montmorillonite mixed clays[J]. Rock and Soil Mechanics, 2020, 41(2): 1-9.

[12] 加瑞, 雷华阳. 有明黏土各向异性固结特性的试验研究[J]. 岩土力学, 2019, 40(6): 1-8. JIA Rui, LEI Huayang. Experimental research on anisotropic consolidation behavior of Ariake clay[J]. Rock and Soil Mechanics, 2019, 40(6): 1-8.

[13] GB/T50123—2019, 土工试验方法标准[S].GB/T50123—2019,Standard for soil test method[S].

[14] 余闯, 刘松玉. 考虑应力水平的软土固结系数计算与试验研究[J]. 岩土力学, 2004, 25(增2): 103-107. YU Chuang, LIU Songyu. Calculation and experiment on consolidation coefficient for soft clay considering different stress levels[J]. Rock and Soil Mechanics, 2004, 25(Suppl 2): 103-107.

[15] 吴雪婷. 温州浅滩淤泥固结系数与固结应力关系研究[J]. 岩土力学, 2013, 34(6): 1675-1680. WU Xueting. Research on elation between consolidation coefficient and consolidation stress of silt in Wenzhou shoal[J]. Rock and Soil Mechanics, 2013, 34(6): 1675- 1679.

Experimental study on anisotropic consolidation behavior of Shanghai clay

NI Jing1, ZHU Congwei1, HAN Yuqi2, HAO Ganglai1

(1. School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China;2. Shanghai Shenyuan Geotechnical Engineering Co., Ltd., Shanghai 200021, China)

In order to investigate the anisotropic consolidation characteristics including consolidation coefficients, volume compressibility coefficients and permeability coefficients, the incremental-loading consolidation tests were conducted on vertical and horizontal undisturbed Shanghai clay samples. The test results show that the relationship between consolidation coefficients and consolidation stresses can be represented by concave curves and the consolidation coefficients of the horizontal samples are slightly higher than the vertical ones. In addition, the consolidation stress corresponding to the minimum consolidation coefficient for the horizontal sample is smaller than that of the vertical one. In the natural deposition process, the flake soil particles unite in the horizontal direction into flocculent structure to form Shanghai clay, leading to larger void ratios for the horizontal samples than the vertical ones, and therefore larger horizontal permeability coefficients than the vertical ones. However, the horizontal compressibility is smaller than the vertical one, as the axial force applied is in the different direction from that of the flake soil particles for vertical and horizontal samples respectively. The results not only promote the better understanding of the anisotropic consolidation properties of Shanghai clay, but also provide certain references for engineering construction in Shanghai clay area.

Shanghai clay; consolidation characteristics; anisotropy; consolidation coefficient; compressibility; permeability coefficient

TU447

A

1672 - 7029(2020)11 - 2782 - 07

10.19713/j.cnki.43-1423/u.T20200063

2020-01-16

国家自然科学基金资助项目(51608323)

倪静(1983-)，女，上海人，副教授，博士，从事土动力学及软土地基加固研究；E-mail：wendy_1943@163.com

(编辑 涂鹏)