液黏离合器摩擦副对流换热系数数值模拟研究

代吉超， 崔红伟,2,3*， 常宗旭,3， 王其良， 李 隆

(1.太原理工大学机械与运载工程学院, 太原 030024； 2.浙江大学流体动力与机电系统国家重点实验室, 杭州 310058； 3.太原理工大学煤矿综采装备山西省重点实验室, 太原 030024)

液黏离合器是利用油膜的剪切力和摩擦表面之间的相互接触来传递动力的一种传动装置,具有无级调速、减小启动冲击、过载保护等功能[1],目前主要应用于重载刮板输送机的柔性启动以及风机、水泵等设备的调速[2]。

液黏离合器摩擦副在柔性启动过程中,因摩擦片和钢片剧烈的相对滑动,会产生大量的热量,使摩擦副的温度急剧升高,引起摩擦副的结构变形,严重影响液黏离合器的工作性能[3]。所以对摩擦副的散热尤为重要,而对流换热系数是准确计算散热量以及预测部件温度的关键。

对流换热系数以前主要是由经验公式来计算,在计算过程中对结构的简化较多,准确性较差。对流换热系数的影响因素很多,它是一个随众多因素变化的复杂函数[4]。目前对流换热系数没有一个权威的定义,牛顿冷却定律给出了对流换热系数的定义式,但它既没有使工程上对流换热系数的计算简化,也没有揭示各相关因素对换热系数的影响规律,它只是将传热计算的复杂性转移到了对流换热系数的求解上。所以在工程上计算传热时,主要的工作就是计算对流换热系数。

目前,中外学者研究了许多结构的对流换热系数,主要用的是解析法和数值分析法。夏德茂等[5-6]建立了火车制动闸片三维模型,采用瞬态分析方法研究了闸片与空气散热面的对流换热系数随制动时间的变化规律。王国林等[7]采用耦合传热的方法,分析了轮胎空气耦合表面各种工况下的对流换热系数分布,总结出轮胎表面几何形状对换热系数的影响规律。McPhe等[8]利用解析法对某翼片制动转子的对流换热系数进行求解,总结了影响因素和经验公式。石宏岩等[9]采用了Beijan提出的新计算模型,通过数值模拟的方法计算了品字形三圆管在空气中自然对流的表面换热系数。片锦香等[10]为了提高对流换热系数的计算精度,建立了机械主轴的瞬态温度场数学模型,提出了一种基于蜂群算法确定对流换热系数的方法,并进行试验验证了方法的有效性。Belhocine等[11-12]以汽车制动盘为对象,利用计算流体动力学(computational fluid dynamics,CFD)分析确定制动盘瞬时状态下各表面对流换热系数随时间的变化规律,然后将对流换热系数作为初始条件进行了盘温分析。

虽然已有很多研究人员对换热系数做了研究,但是目前针对复杂油槽摩擦副的研究较少。现以双圆弧油槽摩擦副为对象,采用CFX仿真分析方法,针对液黏离合器的工作状况,精确计算了双圆弧油槽摩擦副与工作油间的对流换热系数,并研究了该系数的分布情况及主要影响因素。

1 液黏离合器摩擦副结构

液黏离合器含有多个摩擦副,由摩擦片和钢片相间分布组成。摩擦片由摩擦基片和摩擦衬片构成,摩擦衬片分布在摩擦基片两侧。摩擦副结构如图1所示。

为了提高摩擦副与油液之间的对流换热效果,摩擦衬片表面开有双圆弧油槽,油槽深度d1=0.5 mm,散热油液主要存在于双圆弧油槽中。由于花键对换热几乎没有影响,对其进行合理简化。摩擦衬片模型如图2所示。

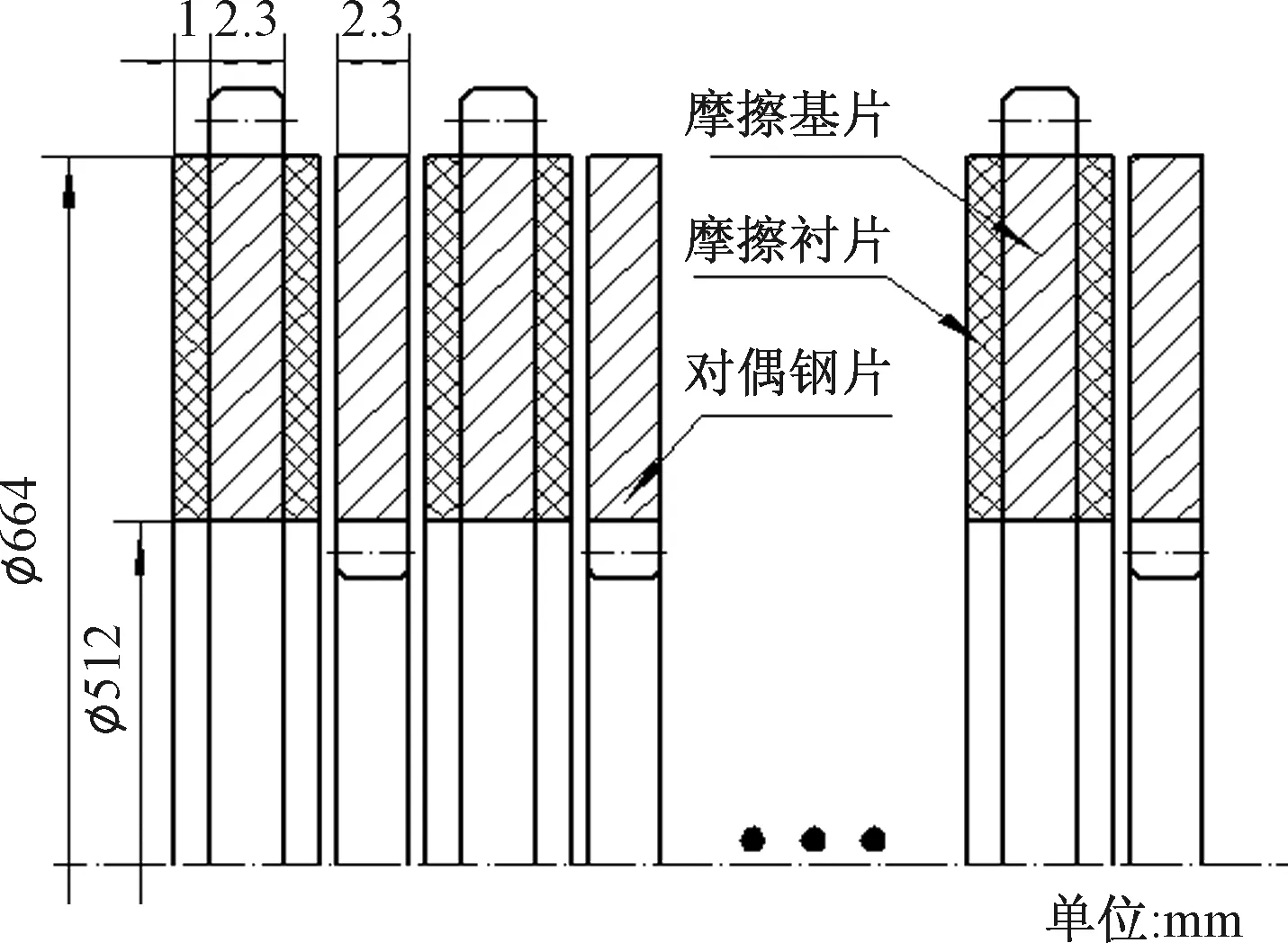
图1 摩擦副示意图

图2 摩擦衬片模型

2 数值仿真求解

2.1 对流换热控制方程

当摩擦副被环形油缸压紧时,摩擦片和钢片的表面微凸峰接触并相对滑动,势必会产生摩擦热。摩擦副之间的间隙非常小,可以认为相互接触,间隙内几乎没有油液。液黏离合器运行过程中主要采用油槽里的油液进行散热。摩擦副和油液之间的对流传热满足流体动力学中的连续性方程、动量方程和能量方程。

连续性方程：

(1)

动量方程：

(2)

能量方程：

(3)

无内热源的固体三维瞬态热传导控制方程为

(4)

式(4)中：C为比热容；Ts为固体温度；ks是固体材料导热系数。

摩擦衬片、钢片和油液交界面处的温度和热流密度相等,即

Ts=Tf

(5)

(6)

2.2 CFX模型及边界条件

2.2.1 CFX模型

取一对摩擦副为研究对象。厚度方向上,由于摩擦副结构和导热的对称性,可以认为摩擦片和钢片在一半厚度的截面上没有热交换,钢片和摩擦基片各取一半的厚度,中心面设为绝热边界条件[13]。又由于摩擦片是旋转对称结构,每2°为一个周期,建立摩擦副1/180模型。

图4 摩擦衬片边界条件

将摩擦副模型导入ICEM中,为简化计算并保证计算精度,细化流体与固体接触区域的网格。流体各表面均控制最大尺寸0.1 mm,设置全局最大单元尺寸0.5 mm,采用四面体划分方法对摩擦副进行网格划分。模型共含2 425 715单元,490 614节点,如图3所示。

图3 摩擦副模型

2.2.2 边界条件

2.2.2.1 摩擦副固体域

假设摩擦片和钢片各个区域温度一致,给定其初始温度为T0=50 ℃。摩擦衬片是纸基材料,摩擦基片和钢片材料为65Mn,材料热物理性能参数如表1所示。

表1 摩擦副热物理性能参数

(1)摩擦衬片：内、外圆周面均采用绝热边界条件,如图4所示；上、下截面设置为周期性边界条件,旋转轴为摩擦副的中心轴；与摩擦基片接触的一侧设置为传导传热,油槽面与油液进行对流换热,各个菱形面与钢片进行传导传热。

(2)钢片和摩擦基片：与摩擦衬片和油液有接触的面都设为传热界面,其余面均设置为绝热边界。

2.2.2.2 流体域

工作油初始温度设定为25 ℃。油液的热物理性能参数如表2所示。

表2 油液热物理性能参数

设置入口压力Pi=0.1～0.3 MPa,出口静压Po=0；油液设为不可压缩流体,如图5所示。上、下截面(7对)分别周期循环对称,统一设置为周期性边界条件,旋转中心为摩擦副中心轴。剩余各接触面设置为对流换热边界。

2.2.2.3 接触面区域

各部件之间建立接触面,与流体接触的流体域耦合面设置为光滑、无滑移的边界条件。设置各接触面传热方式为“保守的界面通量”,网格连接设置为“GGI”。

图5 流体边界条件

2.3 求解设置

设置分析总时间t=2 s,载荷步0.2 s。根据流体和固体的温差及材料的热物理性质计算热流量及热流密度,依据牛顿冷却公式,计算与流体接触各面的对流换热系数hconv为

(7)

式(7)中:qw为热流密度。

3 结果分析

3.1 摩擦副温度场仿真结果

图6所示为摩擦副温度场云图,可以看出,油液对摩擦副的散热效果显著。油液从内径流向外径方向的过程中不断吸热,流固温差不断下降,所以靠近出口部位的散热效果比入口部位差。

图6 摩擦副温度场分布

从图6(a)可以看到,在摩擦衬片的菱形区域,中心部分比外围部分温度高,易形成热斑,这是因为菱形区域外围部分更靠近流体,散热效果好。对比图6(c)和图6(d)发现,由于在轴向方向上钢片直接与流体接触,而摩擦基片和油槽间隔有d2=0.5 mm厚的摩擦衬片,摩擦衬片的导热系数仅为8.2 W/(m·℃),所以摩擦衬片的散热效果整体上比钢片差,但温度场分布情况相似。

3.2 对流换热系数

设置入口压力Pi=0.3 MPa,油液黏度η=0.06 Pa·s。图7所示为油液的流速图,图8所示为流固换热面对流换热系数云图。从图7可以看到,油槽交叉部位的流速明显高于其他区域。这是由于两油槽交叉部位的横截面积小于两个油槽横截面积和,所以流速在此处迅速加快。径向方向上,由于油槽数量相同,油槽横截面积几乎没变,所以流速在两油槽交叉部位基本相同；其余部位流速处于较低水平,流速也基本相同。

图7 流速

图8 对流换热系数分布

通过对比换热系数云图和流速图,可以看出，流速与换热系数有很大的相关性。如图8所示,从内径到外径方向依次取7个交叉处中心点,研究此单位面积上的对流换热系数。7个点处数值如图9所示。

图9 径向对流换热系数分布

从图9可以看出,对流换热系数在摩擦副半径方向上波动不大,波动是因为网格划分和计算误差等因素。

3.3 对流换热系数影响因素分析

当只改变摩擦副的初始温度,散热相同时间后的温度场会发生改变,但是换热系数无任何变化,说明摩擦副和油液的温差只对单位时间内的散热量有影响,对对流换热系数没有影响。以下将详细阐述对流换热系数的几个影响因素。

3.3.1 油液入口压力

油液入口压力对换热系数有较大的影响。假定油液动力黏度η=0.06 Pa·s保持不变,逐渐增大油液的入口压力,分别计算流固接触面的平均对流换热系数和油槽中油液的平均流速,结果如图10所示。从图10中可以看到,随着压力的上升,油槽内的流速加快,单位时间内带走的热量随之增加,进而使对流换热系数变大。

3.3.2 摩擦片转速

设置入口边界条件为总压入口Pi=0.1～0.3 MPa,油液动力黏度η=0.06 Pa·s。从图11可以看到,随着摩擦片旋转速度增加,对流换热系数显著增大。这是因为摩擦片旋转时,一方面离心力会使油液流速加快,另一方面也会改变油液的流动状态,对油液的散热起到了促进的作用,增强了散热效果。

图10 油液流速和平均对流换热系数随入口压力的变化

图11 平均对流换热系数随转速变化

3.3.3 油液黏度

首先,利用黏度测定器测得工作油的黏温特性，如图12所示。根据油液温度Tf变化范围为30～60 ℃,可以得知油液的动力黏度η为0.03～0.10 Pa·s。

图12 工作油黏温特性

图13 平均对流换热系数随黏度变化

改变工作油的黏度,计算流固换热表面的平均对流换热系数。图13所示为不同压力下平均对流换热系数随黏度的变化。从图13中可以看到,随着黏度的增加,平均对流换热系数逐渐降低,油液黏度与对流换热系数负相关。因为当油液的黏度升高,壁面对油液流动的阻力越来越大,导致流速降低,进而影响到对流换热系数的大小。

随着油液黏度的增大,平均对流换热系数下降得越来越慢。这是因为传热方式不仅有对流传热,还有传导传热。当黏度变大,流速降低,对流传热带走的热量逐渐减少,传导传热所占的比重逐渐增大,所以黏度增加到一定程度,对换热系数的影响会减弱。

3.3.4 油液比热容和导热系数

设置油液入口压力Pi=0.3 MPa,出口静压Po=0 MPa,动力黏度η=0.06 Pa·s,分别改变油液的比热容和导热系数,分析它们对换热系数的影响。

不同型号工作油的比热容范围在1 600～2 100 J/(kg·℃)[14],等间隔取样本点进行仿真分析,结果如图14、图15所示。

从图14、图15可以看到,油液的比热容和导热系数越大,换热系数越大。所以在选用油液的时候,为了保证散热效果,可以选择比热容和导热系数较大的油液,同时对油液的热物理性能提出了更高的要求。

图14 平均对流换热系数随比热容变化

图15 平均对流换热系数随导热系数变化

4 结论

以液黏离合器摩擦副为研究对象,利用CFX计算流体动力学仿真软件,获得摩擦副的对流换热系数和温度场分布,并研究了摩擦副对流换热系数的影响因素，得出如下主要结论。

(1)摩擦副温度从内径到外径逐渐变高,菱形区域中心温度高于周边温度,易形成热斑。

(2)油槽交叉部分流速快,对流换热系数大于其他部位；半径方向上对流换热系数变化较小。

(3)在散热过程中,油液入口压力、摩擦片旋转速度和油液黏度变化会影响油液流速和流动状态,从而对换热系数产生影响。为提高散热效果,应选用比热容和导热系数大的油液。