航向已知条件下纯方位跟踪的可观测性
李洪瑞
(江苏自动化研究所,江苏连云港 222061)
1 引言
纯方位跟踪(bearings-only tracking,BOT)也称目标运动分析(target motion analysis,TMA),是条件可观测性系统,其可观测性和跟踪效果依赖于观测平台的机动(方式)[1–2],因此BOT问题研究的核心内容除了目标跟踪算法外还包括系统的可观测性、观测平台机动方式[3–4],多年来,已经开展了许多卓有成效的研究.可观测性是BOT的基本问题,已获得许多结果,例如由观测器加速度矢量、初始时刻目标相对位置和速度矢量的关系表达的可观性条件[1]、仅用(测量的)方位表达的可观测性条件[5]以及目标N–阶多项式运动假设条件下[6]、匀速圆周和匀加速直线运动假设条件下[7–9]的可观测性条件和不可观测条件[10]等.在BOT算法方面,从早期的确定性解算到以极大似然为基础的批处理算法[2–3],从线性/非线性最小二乘滤波到以卡尔曼滤波为基础的各种先进滤波算法等[11–13],系统性能不断得到改进.在观测平台机动研究方面,以费希尔信息矩阵为指标并应用现代最优控制理论获得了观测器常速率下的理论最优航向[14],以及在观测器机动约束[15]和战场威胁环境约束[16]条件下获得的更符合实际的观测站优化轨迹等.文献[17]以几何因子为优化指标,获得了纯方位多目标定位问题中多运动平台的最优布局算法.
虽然BOT问题的研究取得了许多成果,但是在精度、反应时间、对观测器机动(方式)的依赖以及不同条件或背景的应用等方面还不能完全满足实际需求,目前国内外仍有许多不同兴趣点的研究[17–19].由于BOT需要观测器进行有效机动,这个过程一般需要耗费较长的时间,影响观测平台占位和系统的应用.在实际中,通常存在已知目标的某些先验信息的情况,利用先验信息的BOT有利于提高应用系统性能[20],在文献[21]中利用目标前后段“等速”的先验条件,在观测器不机动情况下得到了分段常速运动目标的参数估计.然而,利用先验信息的BOT仍是有条件的可观测系统,当前,在不同先验信息条件下已得到了由观测器和目标运动参数关系表达的可观测条件、观测平台匀速直线运动时的可观测条件等[2–3,21],条件表达较为复杂.
本文研究已知目标航向条件下BOT的可观测条件,在对BOT观测方程通过数学处理成线性系统后,将推导观测系统Gram矩阵行列式的解析表达式,并得到由观测方位和已知航向表示的简洁的系统可观测的充要条件.然后研究了不可观测系统的观测器运动形态,证明了系统不可观测的充分必要条件.最后通过数字计算例,对本文研究结论进行了数字验证和直观展示.
2 问题描述
目标及观测器态势如图1所示,设运动目标T作匀速直线(constant velocity,CV)运动,且已知其航向为Ct,观测器平台O为运动平台(速度非0).由于目标航向已知,故设状态向量为

其中:xt,0,yt,0为初始时刻(t0=0时刻)目标位置坐标;Vt(0)为目标航速;右上角T表示向量或矩阵取转置.显然Xk为时常量.

图1 目标与观测器运动态势Fig.1 Kinematic situation of target and observer
将方位测量方程进行适当数学变换,可得到如下线性状态观测系统:
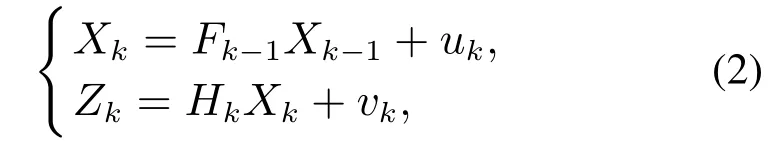
式中:Fk=I3×3为3阶单位矩阵,

xo,k,yo,k为tk时刻观测器坐标;Bk为tk时刻测量的目标方位,其测量方程为
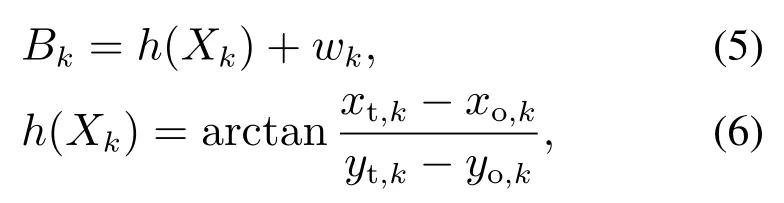
式中:xt,k,yt,k为tk时刻目标的直角坐标:xt,k=xt,0+tkVtsinCt,yt,k=xt+tkVtcosCt;uk,vk,wk为误差项.本文主要研究系统的可观测性理论,因此不考虑系统的各种误差,即假设各误差项都为0(或0向量).
根据现代控制系统理论,在观测时间[t1,tm]内观测系统(2)可观测性判别的Gram矩阵为
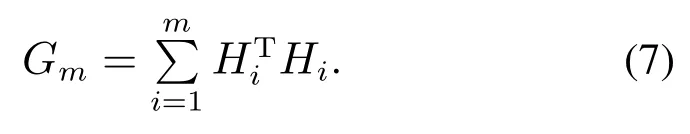
本文将对|Gm|的表达式进行推导,将得到观测系统(2)可观测或不可观测的充分必要条件.
3 可观测性定理
定理1观测系统(2)可观测的充分必要条件为:存在,使得

式中∆(i,j,k)称为可观测判别式,它与Ct有关,因此若需区分Ct时可写成∆(Ct,i,j,k).
BOT可观测的最少测量个数是4个[2,5],从定理1可知,已知目标航向的BOT可观测的最少测量个数减少为3个.
定理1的证明较复杂,将在第4节给出.这里先给出由它得到的3个推论.为此,记

式中方位的双下标表示两方位取差,即Bij=Bj −Bi.当i,j,k中存在任意两个相等或3个全相等时,函数Γ(i,j,k)的值为0/0 型表达式,在本文并不需要讨论它,因此后续关于Γ(i,j,k)的描述或结论中,如没有特别说明,都默认假设所涉及的正整数指标i,j,k等互不相等.

4 可观测性定理证明
为证明定理1,先给出求Gm行列式解析式的引理1,其证明详见附录C.

5 进一步研究



由定理2可得如下推论.
推论4若观测器匀速直线运动,则观测系统(2)不可观测的充分必要条件是式(23)成立.
BOT系统在观测器匀速直线运动情况下是不可观测的[2],而从推论4可知,已知目标航向的BOT系统仅在观测器与目标运动轨线平行时不可观测,这点更符合观测器占位的需求[3,20],理论上只需避免观测器航向与目标同向或反向.
推论5观测系统(2)可观测的充分必要条件是:对所有互不相等的i,j,k均有

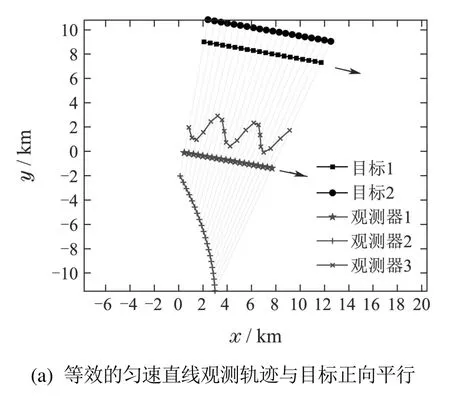
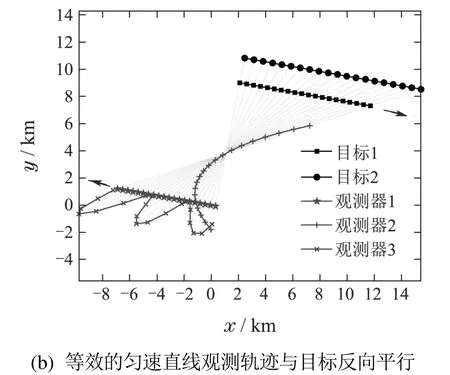
证根据推论2,观测系统(2)可观测的充分必要条件是存在1i0 给出4个数字计算例,分别对可观测性判别矩阵行列式、不可观测、可观测等实例进行直观展示与验证. 例1可观测性判别矩阵行列式的数字计算例.通过固定目标参数、改变观测器运动参数的方式对各种态势进行枚举.设观测采样次数m=20∼200,采样时刻为tk=10k(s).目标1运动速度、航向分别为5.144 m/s,100◦,初始位置为(2000 m,9000 m),其运动方程为 目标2是与目标1平行的匀直运动目标,其运动方程为 目标选取为目标1或目标2,观测器速度在(0 m/s,50 m/s)、航向和初始方位B0在[0◦,360◦]范围、初始距离D0在[1 km,40 km]范围随机选取,得到观测器初始位置坐标为xo,0=xt,0−D0sinB0,yo,0=yt,0−D0cosB0,这样保证了各种态势能得到枚举,数字计算中当式(15)左右两边计算误差低于1.0×10−8时视为相等.共进行106次蒙特卡洛计算,计算结果均显示式(15)成立,在观测器航向等于100◦或280◦时,式(15)左右端等于0,这也间接验证了定理1的正确性. 例2观测器匀速直线运动轨迹的不可观测计算例.观测器的航向在100◦和280◦中随机选取,观测器其余运动参数(速度和初始位置坐标)按照数字计算例1选取,枚举观测器轨迹与目标轨迹平行的各种态势.共进行106次蒙特卡洛计算,均得出|Gm|=0,表明系统不可观测.计算结果验证了定理2 的正确性. 例3观测器复杂机动运动轨迹的不可观测计算例.仿真结果如图2所示.图2(a)中3个观测器运动方程分别为 图2(a)、图2(b)中,观测器1与目标的运动轨线平行(图2(a)正向、图2(b)反向),而观测器2、观测器3具有复杂的运动轨迹.图2(a)、图2(b)都显示了观测器1,2,3对目标1,2 的观测都得到了相同的方位观测量(即多个观测器对多个目标得到相等的方位观测量),可见3个观测器是等效的,并且由于3个观测器中任意一个对2个(实际上有无穷多个)目标的方位观测量相同,说明3 个观测系统是不可观测的,即便观测器2、观测器3具有复杂的运动轨迹. 图2 观测器具有复杂运动轨迹的不可观测态势Fig.2 Unobservable kinematic situation with complicated observer motion trajectory 事实上,从观测器的运动方程可以看出,式(37)或式(40)为时间的线性函数,式(38)或式(41)为时间的二次函数,式(39)或式(42)为含时间的正弦运算的复杂函数,但是稍加计算便能够得到: 可见不同观测器对不同目标观测得到的方位观测量相等. 数字计算例3验证了定理2的正确性,同时这也表明复杂的观测器运动并不能保证系统的可观测性.在系统设计中,即便已知目标航向,观测器的运动方式的确定也应当予以重视. 例4BOT计算例.目标初始位置、航速、航向分别为(2083.78 m,11817.69 m),7.72 m/s,135◦.为了进行比较,考虑航向已知和未知的情况.观测器1平台为匀速直线运动,运动参数为:初始位置(0.00 m,0.00 m)、航速6.17 m/s、航向10◦.测量误差为0.3◦.观测器2初始运动参数与观测器1相同,在第3分钟和第5分钟进行了转向机动,航向分别为300◦和50◦.对目标的跟踪考虑3种条件:1)航向已知,采用观测器1的信息;2)航向未知,采用观测器2的信息;3)航向已知,采用观测器2的信息.估计方法则由式(2)采用线性最小二乘法,进行100次蒙特卡洛仿真计算,结果如图3所示. 从仿真结果可知,在航向已知的情况下,无需观测平台进行机动,得到了目标的运动参数.与目标航向未知而通过观测器机动获得可观测条件进行目标运动参数计算相比,前者所需观测时间更短,在同样观测时间情况下精度更高.如果目标航向已知,同时观测器进行有效机动,则目标运动参数精度进一步提高.在本例中,由于目标和观测平台运动航向不满足式(23),因此BOT系统可观测,这也间接验证了定理1–2的正确性. 图3 不同条件下BOT误差Fig.3 Errors of BOT for different conditions 在纯方位观测系统中利用已知的目标航向进行目标跟踪,其主要目的是期望系统可观测,而无需观测平台机动,有利平台占位,缩短系统反应时间.本文从方位测量关系和观测器平台运动方式研究了系统的可观测性,通过详细推导观测系统的Gram矩阵行列式,得到并证明了系统可观测的判断准则,并分析出了不可观测系统的目标与观测器运动态势特征. 这种由已知航向和方位测量关系表示的可观测性判断条件,可为被动观测系统设计提供指导.而由目标航向与观测器航向关系的可观测性判别条件,可为观测平台的运动控制提供参考. 工程实际中,目标运动方式会更加复杂,例如匀加速直线运动、匀速圆周运动等,相应的可观测条件尚待研究. 附录A 可观测判别式性质 本文用到的关于可观测判别式∆(i,j,k)的两个性质: 性质A1可观测判别式∆(i,j,k)对各个变量具有反对称性,即交换∆(i,j,k)中任意两个变量的顺序,相应函数值改变符号: 这可应用三角函数性质推导出来.由性质A1很容易推导出如下性质A2. 性质A2若变量i,j,k中存在两个相等,则∆(i,j,k)=0,即 附录B Γ(i,j,k)性质 本文用到的关于Γ(i,j,k)的3个性质: 性质B1交换i,j,k中的任意两个变量,Γ(i,j,k)的值不变,即 根据式(10),结论显然. 性质B2若方位序列存在等效的匀速直线观测轨迹,则改变i,j,k中的一个变量的值而其余两个变量不变时,Γ(i,j,k)的值不变,即 证根据性质B1,只需证明Γ(i,j,k)=Γ(i,j,l).为此,计算Γ(i,j,l)−Γ(i,j,k)的分子∆Γijkl,得 附录C 引理1的证明 为了证明引理(即式(15)),将式(3)代入式(7),可得到Gm的表达如下:6 数字计算例



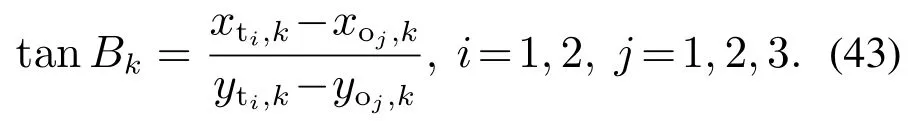

7 结论