考虑通信时滞的分布式电力经济调度算法设计

孙妙平,姜 波

(中南大学自动化学院,湖南长沙 410000)

1 引言

经济调度问题是电力系统中最基本也是最重要的问题之一,它本质上是一个优化问题.传统的解决经济调度问题的算法可以大致分为两类,一类是分析法,包括牛顿迭代算法[1]、梯度下降搜索算法[2]等;另一类是在现代优化理论基础上建立起来的算法,如遗传算法[3]、粒子群算法[4]等.这些算法属于集中式调度算法,需要一个中心控制器来协调各个局部单元,当网络中某个节点发生故障时,中心控制器难以对故障节点进行处理,网络的即插即用性能也不好.另外,随着网络规模的增大,中心控制器的通信负担增加,需要更高的通信成本,且由于中心控制器需要获取所有局部发电单元的信息,使得信息在传递过程中容易泄漏[5].因此,分布式算法广泛用来解决电力系统中的经济调度问题.

近年来随着多智能体分布式算法的发展,涌现出了许多基于分布式理论的经济调度算法.文献[6]设计了一种以增量成本为一致变量的分布式电力经济调度算法,但是需要一个领导节点获得系统的不匹配功率.文献[7–8]提出了一种引入创新项来确保功率供需平衡的分布式调度算法,并可利用该项来修正每台发电机的输出功率.文献[9–10]设计了一种每台发电机可计算自身的局部供需不平衡功率来调整输出功率的分布式一致性算法.文献[11]考虑网络拓扑结构发生变化,设计了一种基于供需平衡的分布式算法,但是要求每个发电机获取邻居的成本增量信息.文献[12]提出了一种解决一般凸成本函数的电力系统经济调度算法,但是需要知道总负载需求.文献[13–14]通过把负载节点并到相邻的发电机节点来解决功率失衡的问题.文献[15]设计了一种有限时间收敛算法,但是只能解决二次型成本函数系统的优化问题.文献[16]设计了一种考虑智能体输出约束的算法,把输出约束在一个凸集内部.值得注意的是,以上分布式算法都没有考虑邻居间交换信息产生的通信时滞对算法的影响.

事实上,在实际电力系统中,这种通信时滞是不可避免的,它的存在会导致系统动态性能变差,甚至使得算法不收敛[17–18],因此在设计分布式算法时,必须考虑时滞对算法的影响.文献[19–20]考虑二次型成本函数,提出了一种只考虑常数时滞的分布式经济调度算法.文献[21]考虑时变拓扑和通信时滞,提出了一种梯度push-sum解决问题,但是当时滞上界较大时会产生很多虚拟智能体,导致算法难以求解.文献[22]设计了一种一致性算法,采用广义拉奎斯特方法判断得到系统稳定的充分必要条件,得到一个严格的时滞上界,但是该算法仅仅对分段常数时滞适应.文献[23]考虑二次型成本函数,得到了时变时滞下算法收敛的充分条件,并设计了一种发电机约束策略,但是该约束策略使得系统收敛速度变慢.

根据以上调研,本文考虑了发电机的输出限制和邻居间交换信息时的通信时滞,提出了一种新的对所有发电成本为凸函数的发电机组成的电力系统都适应的权重平衡图下的分布式经济调度算法,并通过凸分析和Lyapunov理论可以获得算法收敛的充分条件.与目前存在的一些算法相比,本文的算法具有如下的优势:

①文献[15,19–20]的算法只能处理二次可微型成本函数的优化问题,而本文的算法对所有发电成本为凸函数的优化问题都适应,并且不要求该成本函数可微,这就大大增加了算法的应用范围.

②文献[19–20]的算法只考虑了常数时滞,而本文的算法考虑了时变时滞对系统的影响,并采用时滞分割的方法减小了系统保守性.

③文献[15,23]的算法需要供需平衡后才处理发电机输出约束问题,而本文的算法将输出约束考虑在算法里面,因此可以保证在程序运行中每台发电机的输出功率始终保持在限制范围内.

符号说明:Rn表示维向量空间;Rn×m表示n行m列的矩阵空间;A ⊗B表示矩阵A与B的直积;C1×C2表示笛卡尔乘积;

2 预备知识

2.1 图论理论

2.2 凸分析理论

2.3 非光滑优化理论

引理1[16]考虑微分包含

它的平衡点是集合{x ∈Rn|0∈F(x)}.如果对任意的初始条件x0∈S,存在该问题的解x(t),使得x(t)∈S,∀t0则称集合S是该微分包含的不变集.设F:Rn →Rn为凸集C上的集值映射,考虑如下形式的微分包含:

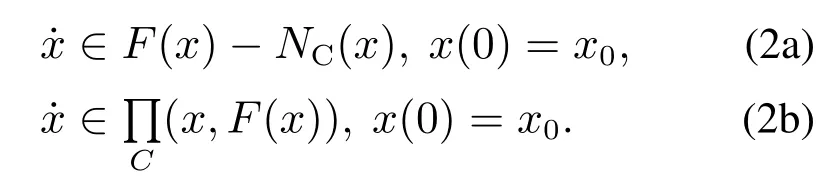
下面两个结论是满足的:

①x是式(2a)的解当且仅当它是式(2b)的解;

②如果F在C上有界,那么式(2a)和式(2b)存在解.

引理2[16]对于一个给定的径向有界正定标量函数V(x),它沿着轨迹(1)的导数为

假设S ∈Rn是式(1)情况下的不变集,V:Rn →R是连续可微函数.如果式(1)中状态量有界,并且LFV(x)0或者LFV(x)=ϕ,对于所有的x ∈S都成立.那么所有从S出发的点,最终收敛于最大不变集M中的点,并且M ⊂S ∩{x ∈Rn|0∈LFV(x)},如果M是有限集,那么每个解的极限都存在且为M中的一个元素.

2.4 矩阵理论

引理3[23](杰森不等式.)对于给定的标量d>0,任意的正定矩阵M和函数f(s)∈L2[−d,0],有下面的不等式成立:

3 电力经济调度问题的数学模型

考虑N个发电机的电力系统,用一个无向图G来描述该系统的通信拓扑.本文的目标是满足电网供需平衡与发电机局部约束,且使得所有发电机的发电成本之和最小,因此,它的数学模型可以描述为

其中:x=col(x1,···,xN),fi(xi)是强凸的,Ci为发电机的输出功率限制.

4 考虑通信时滞的分布式经济调度算法

4.1 分布式电力经济调度算法设计

为了解决经济调度问题(3),并考虑邻居间交换信息时的通信时滞,设计如下算法:

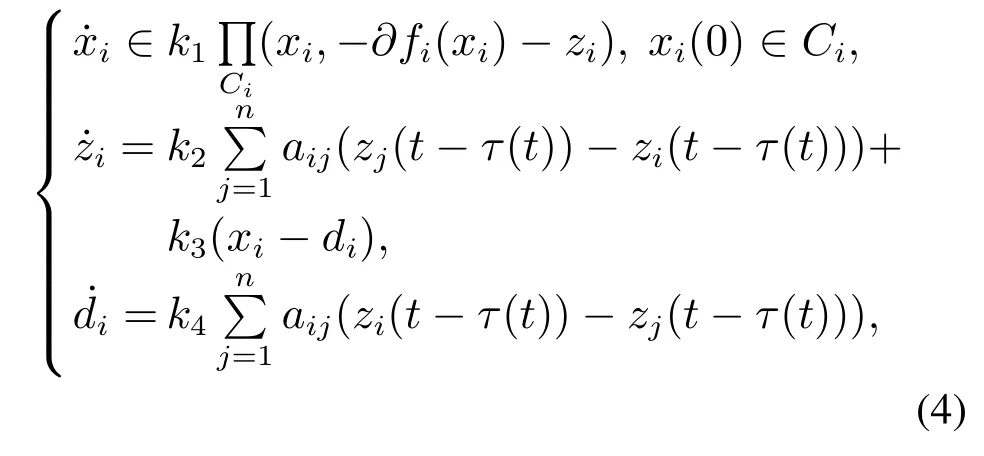
其中:xi是发电机的输出,zi是相邻的发电机之间的共享信息,di为局部虚拟负载.为了简化分析,本文假设各个发电机之间的通信时滞是相同的,均为τ(t),且满足τ(t)∈[0,τ¯],(t)p.ki ∈R+,i=1,2,3,4为系统参数.

为了便于分析,将式(4)表示成更加紧凑的形式:

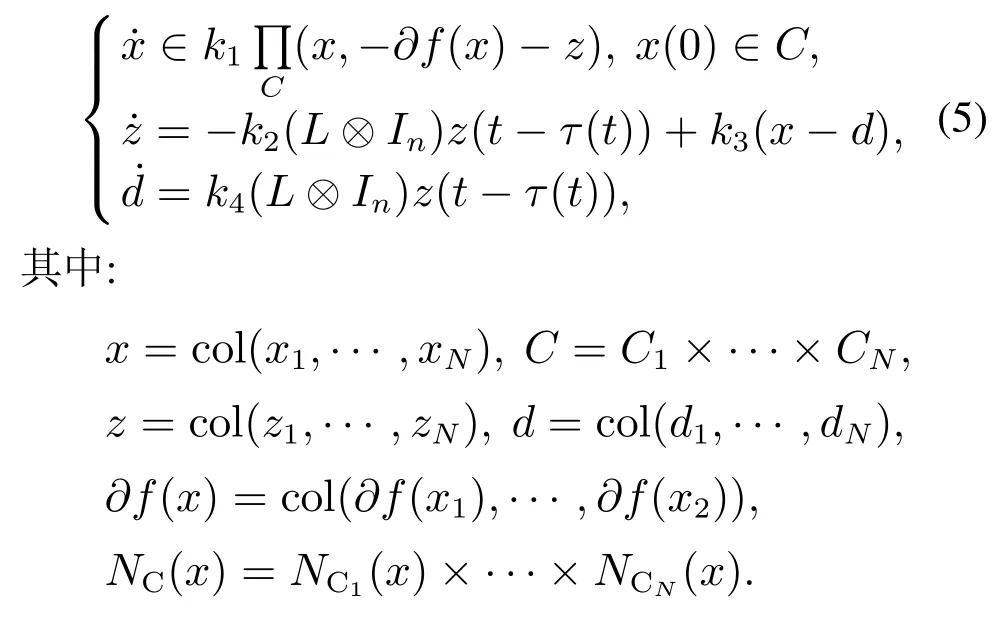
4.2 主要结果

定理1系统(5)平衡状态下的解x∗即是问题(3)的优化解.

证根据引理1,系统(5)达到平衡状态时有

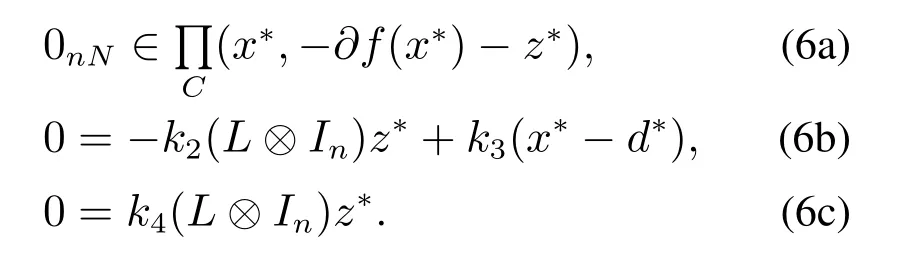
注1因为V的导数中各项整理后不存在系数k1,因此,系统稳定性只受系数k2,k3,k4的影响,进而影响算法的时滞上界.又根据V1的构造可知,参数k1位于标量∥ζ∥2的分母上,k1取较大值时,V的初值偏离原点的距离就相对减小,所以使得系统收敛到原点的时间减小,因此,系数k1对系统收敛速度的影响很大.

5 算例仿真

考虑一个五机电力系统,它的结构示意图和通信拓扑图如图1–2所示.

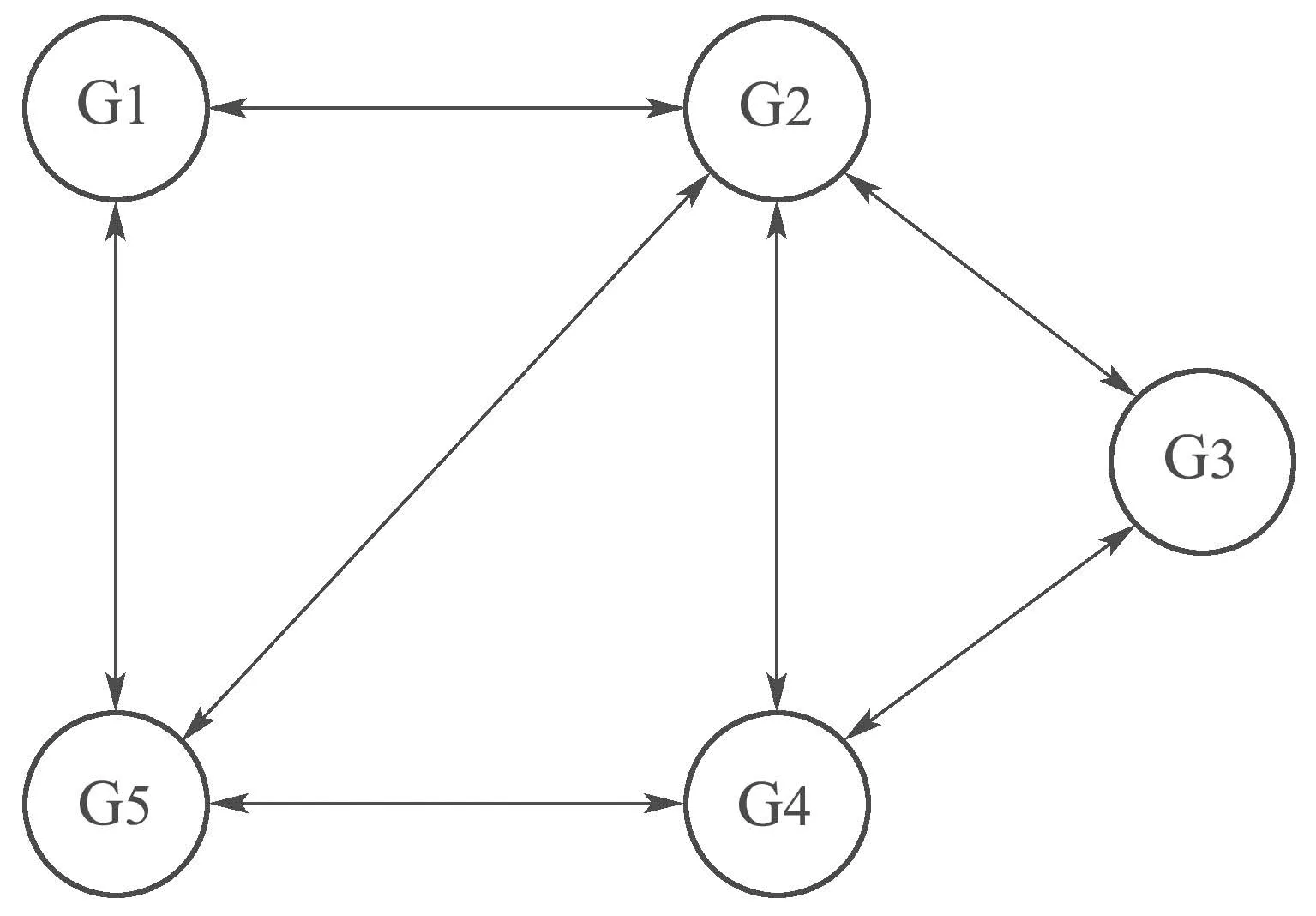
图1 五电机通信网络图Fig.1 The Communication topology with fvie generators

图2 五电机电力网络图Fig.2 The single-line diagram of power grid with fvie generators

每一台发电机的成本函数及输出功率限制如表1所示,其中发电机G1是风力发电单元.

表1 发电机成本函数和输出限制Table 1 The cost functions of generators and their output constrains

情况A假设k2=k3=k4=k,给定时变时滞导数最大值p为0.8,取τ(t)=+0.08|sin(10t)|,分析k1和k的变化对时滞上界和系统收敛速度的影响.假设负载总功率需求为250 MW,仿真结果如表2–3所示.

从表2可知,当k1固定时,参数k的取值对时滞上界和收敛速的影响很大,当k的取值越大时,时滞上界越来越小,但收敛时间变短,即收敛速度加快.从表3可知,当k固定时,参数k1的变化对时滞上界几乎没有影响,但是k1取值增大时,算法的收敛速度明显加快,这与注里的分析一致.但是无限增大k1并不能保证系统收敛速度一直加快,当增加到某一数值时,算法的收敛速度几乎不再变化.

表2 k1固定,参数k对系统性能影响Table 2 The influence of parameter k on system performance with fixed k1

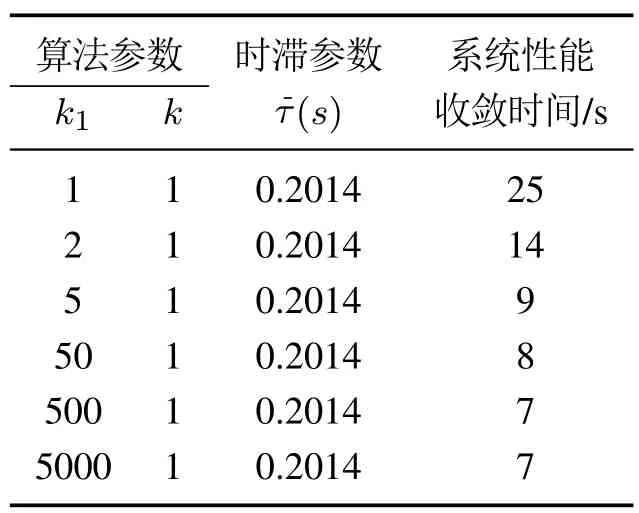
表3 k固定,参数k1对系统性能影响Table 3 The influence of parameter k1 on system performance with fixed k

情况B取k1=5,k=1,=0.1214 s.

情况b1算法有效性验证,仿真结果如图3–4所示.

从图3可以看出系统在8 s时达到稳定,各个发电机的局部变量zi收敛到一致,在t=8 s时z∗=−30.84,各个发电机的输出始终限制在允许的范围内,且满足系统的供求平衡,达到稳定时发电成本为0.191$/kWh,这表明所提算法是有效的.但是,当超出允许的时滞上界时,算法不再收敛.

图3 一致性变量轨线图Fig.3 The trajectory diagrams of consensus variables

图4 发电机输出功率曲线Fig.4 The power output curves of generators

情况b2系统在t=9 s时切除发电机G3,在t=18 s又将发电机G3重新投入,所得的仿真结果如图5–6所示.

图5 发电机G3切除–投入情况下变量z变化曲线Fig.5 The curves of variable z when G3 is cut off and switched on

图6 发电机G3切除–投入情况下输出功率变化曲线Fig.6 The power output curves when G3 is cut off and switched on

显然,在G3没有切除时,t=8 s时系统稳定,各个发电机的一致变量z收敛到−30.84,此时的发电成本为0.191$/kWh,t=9 s时,切除G3,发电机G3的输出变为0,发电成本为0.2$/kWh.t=15 s时,一致变量重新收敛到−33.09,t=18 s重新投入G3,各个发电机一致变量与输出又恢复到了切除前的状态,这表明本文的算法具有良好的即插即用性能.

情况b3t=10 s时将负载增加50 MW,即总负载从250 MW增加到300 MW得到,仿真结果如图7–8所示.

图7 负载突变情况下参数z变化轨线图Fig.7 The trajectory diagrams of variable z when the loads change suddenly

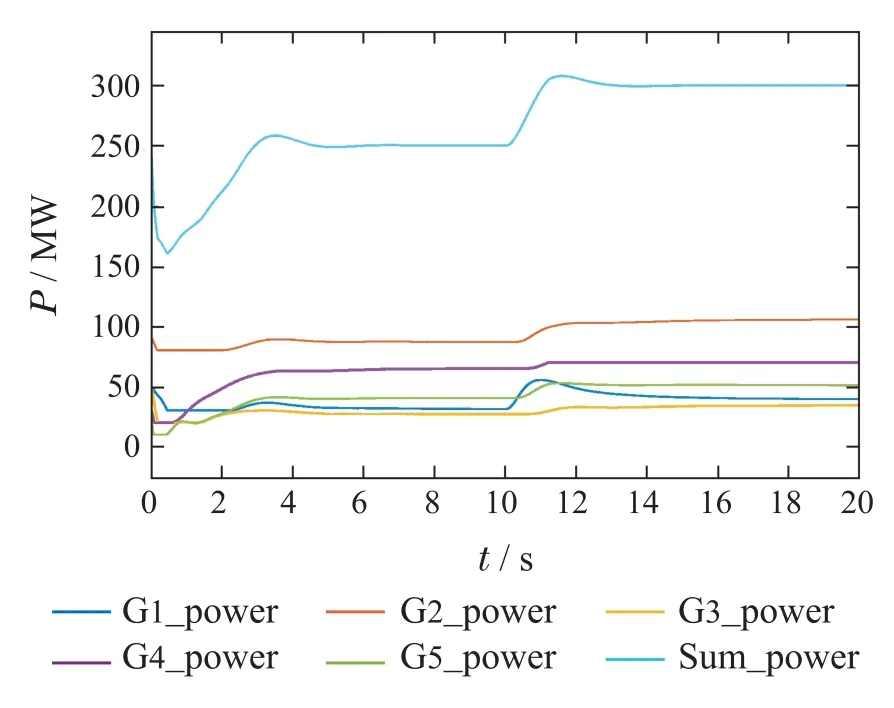
图8 负载突变情况下发电机输出变化曲线Fig.8 The power output curves of generators when the loads change suddenly

从图7–8可以看出,增加负载后各个发电机的输出功率都有增加,且一致性变量z从−30.84变为−35.07,发电成本从0.191$/kWh变为0.204$/kWh.输出总功率与负载需求保持平衡,发电机输出在限制范围内,这说明算法对于负载突变下的情况具有良好的鲁棒性.

情况C与文献[23]中的算法进行比较,取文献[23]中的各个发电机参数和输出限制,考虑与文献[23]中相同的时变时滞函数为τ(t)=0.85|sint|+0.2和总负载需求功率,得到的仿真结果如下图9–10所示.

从图9–10中可以发现,本文设计的算法在程序运行过程中,发电机输出始终保持在限制的范围内,并且以较快的收敛到最优输出状态,算法稳定时间为15 s左右.而文献[23]即使不考虑输出限制,系统稳定时间也需要30 s左右,再加上有多个发电机输出限制的情况下,会使收敛速度更慢,这表明本文所提算法要优于文献[23]中的算法.

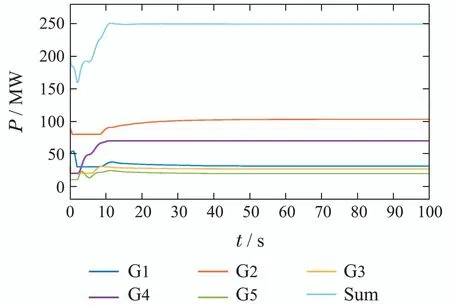
图9 本文发电机的输出功率曲线Fig.9 The power output curves of generators in this paper

图10 文献[23]的发电机输出功率曲线Fig.10 The power output curves of generators in reference 24

6 结论

本文提出了一种新的分布式电力经济调度算法,各个发电机之间不需要交换成本信息,且通过一个方向投影算子解决了发电机的输出约束问题,适应于成本函数为凸且函数不可微的情况,这样应用范围更广.利用时滞分割的方法减小了系统的保守性,增加了系统的时滞上界.仿真结果也验证了算法的有效性和优越性.