求解复杂耦合问题的多系统优化方法

马海平,朱 聪,母佳鑫,孙 超

(1.绍兴文理学院电子工程系,浙江绍兴 312000;2.成都理工大学信息科学与技术学院,四川成都 610059)

1 引言

国务院印发的《新一代人工智能发展规划》中明确强调要围绕新一轮产业变革的重大需求,应用人工智能提升产业发展,大力推进智能系统的集成应用.同时随着工业系统的大规模集成,具有多系统、多目标、多约束、多尺度和不确定特征的复杂耦合问题也随之大量涌现,这对相关领域的传统研究方法提出了挑战.目前针对工业系统中复杂耦合问题的研究已取得很多成果,但仍存在少部分子系统与子系统,或环节与环节之间信息交互与反馈关系不明确,从而难以保证整个问题的全局最优.因此在当今国际竞争激烈与国家重大战略需求环境下,迫切需要寻求更好地求解此类问题的方法和策略,实现局部与整体、短期与长远、效益与安全和环境影响之间的全局优化,为实现我国智能工业打下坚实的基础[1–4].毫无疑问解决产业变革中的复杂耦合问题具有非常重大的现实意义和广泛的应用前景,已成为相关学科的研究热点和重要研究方向.

2 复杂耦合问题

本文中的复杂耦合问题,主要指的是复杂耦合系统中的优化问题,其往往由多个不同功能的子系统耦合而成,每个子系统又包含多个目标和多个约束,同时各子系统之间存在不同程度的交互,比如部分目标相同或变量共享等,其数学模型描述为

式中:Fi为第i个子系统,K为子系统个数,为所有子系统第j个共同目标函数,M0为共同目标函数个数,fik为第i个子系统中的第k个私有目标函数,Mi为私有目标函数个数;为所有子系统第j个共同约束方程,q0为共同约束方程个数,gik为第i个子系统中的第k个私有约束方程,qi为私有约束方程个数;为所有子系统共享决策变量,x为私有决策变量.从式(1)可以看到,该模型是对复杂耦合问题中多个子系统的整体优化.

此类复杂耦合问题具有两个显著特点:一方面,其涉及不同功能的多个子系统,各子系统紧密耦合且耦合关系复杂;另一方面,子系统内部的目标和约束相互冲突,难以调和.因此,不能简单地将复杂耦合问题看成一类传统的单目标优化问题或多目标优化问题,前者只涉及一个目标函数的优化,后者涉及两个或以上相互冲突目标函数的优化.复杂耦合问题包含多个优化子系统,每个子系统又类似于传统意义上的多目标优化问题,也就是说,复杂耦合问题是多个多目标优化问题的集成,这里将其称之为多系统优化问题.但是必须指出,这样的案例实际上大量存在于产业变革的各个方面,比如在云计算环境下,基于多客户按需服务的多级供应链网络就是一个典型的多系统优化问题,包括用于生产制造的多目标车间作业调度子系统、用于产品储存的多目标分配子系统和用于产品派发的多目标旅行商子系统[5–7].该案例的求解任务就是整体优化供应链网络,以期获得各级网络的最优解.

当前,针对复杂耦合问题优化的研究已有一些相似的文献发表[8–9].国外学者Martins等[10]较早研究了多学科耦合系统的设计问题,提出了多学科设计优化(multidisciplinary design optimization,MDO)方法,其主要思想是考虑各学科之间的协同效应,应用有效的优化框架来组织和管理整个系统的求解过程,该方法本质上只是一个设计框架,没有涉及具体的优化机制和实现过程.对于复杂耦合问题,更多的研究者则从设计层面将其转化为多目标优化特别是众目标优化(many-objective optimization,MOO)问题[11],然后在此基础上进行传统的优化求解.张青富等[12]提出一种基于分解的高效计算框架,将一个多目标优化问题分解成一系列单目标优化子问题,然后融合相邻子问题的信息加速求解各子问题.C.A.Coello 等[13]提出了协同进化优化方法,运用生物协同演化的思想和分而自治的策略,通过构造多个种群,建立它们之间的竞争或合作关系来模拟复杂系统的演化环境,以达到整体优化的目的.Y.S.Ong等[14–15]针对多个任务的求解提出了多因子优化(multiobjective multifactorial EA,MO–MFEA)方法,其基本思想是将多个不同任务的解空间统一到一个扩展的解空间中,经过进化操作后,针对不同任务再将统一表示的解集解码到各任务原来的解空间中,从而达到同步优化多个任务的目的,数值仿真结果表明该方法在求解多任务问题上具有很好的性能.

综合分析,求解复杂耦合问题无疑是智能优化方法设计和应用的重要研究方向,非常有必要对其进一步的探索.本文从求解复杂耦合问题出发,借鉴多种群进化算法的智能平行特征,利用种群间进化信息的继承和交互作用,提出多系统优化(multi-system optimization,MSO)方法,同时通过基准函数验证了新方法的高效性和优越性.进一步根据供应链理论和实际需求,建立基于多客户按需服务的三级供应链网络,并将所提出的MSO方法应用到该网络中,仿真结果表明所提出的方法具有很好的优化性能.

3 多系统优化方法

MSO方法的设计原理是借鉴多种群进化算法的智能平行特征,将一个子系统的优化环境用一个子种群来表示,每个子系统通过优秀的进化算子求解一类多目标优化问题,子系统之间则通过变量共享、目标函数和约束条件的相似程度来实现信息迁移与反馈,完成不同子系统内部多个目标的同步优化,从而得到各子系统的全局最优.其基本思想是根据进化信息的继承性和优化环境的关联性,在一个子系统内部产生的优秀解集大概率对其他子系统的优化有很大的正向帮助和启发,从而能够加速子系统全局寻优.基于所述设计原理和思想,一种用于求解复杂耦合问题的MSO方法框架如图1所示,主要包括子系统内部的进化操作和子系统之间的迁移操作,接下去详细阐述各自的实现过程.

图1 多系统优化方法框架Fig.1 The framework of MSO method

3.1 子系统内的进化操作

对于子系统内的进化操作,采用常规的遗传算子,主要包括选择、交叉和变异.其中选择算子采用轮盘赌选择法,其概率的分布与候选解集的秩成正比关系,反映了子系统中不同候选解所对应的相对性能.在多目标优化领域,一般采用经典的非支配排序法来计算候选解集的秩[16].考虑本文提到的复杂耦合问题存在大量约束条件,且在实际问题中,这些约束条件尤为重要,因此有必要在候选解集排序过程中优先考虑约束影响.结合适应度值,修改后候选解集的秩计算如下:首先计算每个候选解的约束冲突数,然后对约束冲突数进行非支配排序,当候选解的约束冲突数相等时,则进一步对其按常规的适应度值进行非支配排序.接下去执行交叉,可以选择均匀交叉、多点交叉等,目的是通过替换或重组生成新的解集.最后执行变异,根据概率随机修改候选解中的决策变量,增加子种群中解集的多样性.需要说明的是,子系统内的进化操作是一个相对独立的演化过程,完全可以采用其他更优秀的进化算子或群体智能算子来提高优化性能.

3.2 子系统间的迁移操作

子系统间的迁移操作是MSO方法的关键技术,其通过变量共享关系、目标函数和约束条件的相似程度来实现不同子系统之间信息的迁移和反馈.整个迁移操作归纳为3步:第1步选择需要迁移的子系统对,第2步在该子系统对内选择需要迁移的候选解,第3步完成它们之间的迁移.

首先根据不同子系统目标值和约束值的相似程度匹配子系统对,也就是说,使用相似程度来决定与迁入子系统构成迁移关系的迁出子系统.根据优化环境的关联性,具有高相似度的子系统对比具有低相似度的子系统对更有可能通过迁移操作而相互受益.不同子系统之间的相似系数SL的计算如算法1所示,其中G和H表示不同子系统内目标函数值或约束值的集合.算法1的目的是在不同子系统集合中,通过比较找到目标函数值或约束值相同的个数,SL值越大,子系统间相似程度越高.

算法1子系统间相似系数的计算.

然后在已获得的相似系数基础上,计算选择迁出子系统的概率,公式如下:

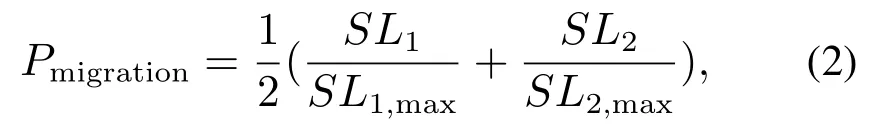
式中:Pmigration为迁出子系统的选择概率,其值越大,被选择作为迁出子系统的可能性越大;SL1,SL2,SL1,max和SL2,max分别为不同子系统之间目标值相似系数、约束值相似系数、最大目标值相似系数和最大约束值相似系数.迁出子系统的选择过程如算法2所示.

算法2迁出子系统的选择.

进一步在已确定迁出子系统基础上选择迁出候选解.本文采用候选解之间的欧氏距离计算迁出候选解的选择概率,然后基于该概率使用轮盘赌法选择迁出对象,过程如图2所示,图中D为根据欧氏距离计算得到的选择概率.这是因为解集间的欧氏距离越大,其种群多样性就越高,从而为找到最优解提供更多可能性.

图2 基于轮盘赌法的迁出解选择Fig.2 Emigrating solution selection based on roulette wheel method

在复杂耦合问题中,由于不同子系统通常具有不同的候选解结构,即决策变量存在不同程度的共享,因此在计算欧氏距离前,解的结构需要一致,以表1中的两个子系统为例,子系统1缺失变量3,子系统2缺失变量2和4.

表1 不同子系统中的候选解结构Table 1 Candidate solution structures in different subsystems

首先要求每个候选解应包含整个问题的所有变量,如果某一子系统中的某一变量不存在,用N/A表示该缺失数据.然后重新定义欧氏距离计算公式为

式中:xik和xjl分别为第i和j个子系统中的第k和l个候选解,∆ikjl为它们之间的距离;n和s分别为候选解长度和决策变量序号.

最后,在确定迁出子系统中的迁出候选解后,执行迁移算子,定义为

两个子系统间的迁移过程如算法3所示.可以看到,迁入候选解的每个决策变量都有可能被其他子系统中的决策变量所替换.整个子系统间迁移操作的优点在于其考虑了一般智能优化方法的共性核心问题—探索与开发的权衡问题,即通过目标值和约束值的相似程度来促进不同子系统的快速寻优,通过解集距离来提高子系统的多样性.

算法3子系统间的迁移.

3.3 方法流程

基于上述设计原理,给出MSO方法的实现步骤,描述如下:

步骤1初始化控制参数:设定子系统数K及对应的子种群大小Ni、交叉概率pc、变异概率pm、迁移阈值概率pv、精英E0以及最大迭代次数T;

步骤2初始化每个子系统,即随机产生相应的候选解集;

步骤3对每个子系统,根据非支配排序法计算每个候选解的秩并按比例计算选择概率,然后按第2.1节所述,依概率执行子系统内的进化操作,包括选择、交叉和变异,或直接移植NSGA–II作为子系统内进化操作的主体;

步骤4基于算法1和式(2)计算不同子系统间目标值和约束值相似系数SL及迁出子系统的选择概率Pmigration,并基于算法2依概率选择需要迁移的子系统对;然后,基于式(3)计算该子系统对内部候选解之间的欧氏距离σ,根据图2计算迁出候选解的选择概率D,并使用轮盘赌法选择需要迁移的候选解;最后,按照算法3完成不同子系统候选解之间的迁移,即根据阈值概率pv判断是否用迁出候选解的决策变量替换迁入候选解对应位置的决策变量,整个子系统间迁移过程的具体执行细节参考第2.2节所述.

步骤5保存每个子系统中的最佳解作为精英,并用上一代的精英替代当代中的最差解;

步骤6如果满足停止准则或最大迭代次数T,输出结果并停止运算;否者,回到步骤3进行下一次迭代,算法4给出MSO方法其中一代的实现过程.

算法4MSO方法其中一代实现过程.

3.4 理论分析

接下去考虑MSO方法的收敛性,根据其设计原理和实现过程,参考文献[17]中多种群多目标进化优化算法的马尔科夫链模型推导过程,由于两者之间的运行机理基本相同而面向对象不同,可以直接得到第i个子系统从种群分布v转移到种群分布u的状态转移概率Pi(u|v)为

式中Ni和ni分别为第i个子系统的种群大小及候选解长度,其中

式中P(1),P(2)和U分别为进化(选择和交叉)、迁移和变异的转移概率,其下标依次为子系统、候选解和决策变量序号.进一步,由于式(6)的结构与文献[18]中的式(11)相同,可以用相同的定理和步骤证明所提出的方法在精英策略下必然收敛.

3.5 方法特点

MSO方法与其他智能优化方法一样,是一种模拟自然现象规律和生物进化机制的优化方法.但是又与其他方法有本质的区别.首先MSO方法与第1节中提到的众目标优化方法比较,区别在于:1)概念不同,已有方法属于多目标优化,本文所提方法属于多系统优化;2)机理不同,已有方法需要对多目标或决策变量进行分解或转换,策略的选择影响优化性能,本文所提方法对复杂耦合问题的优化是一种自然行为,即无需先验知识,根据问题建立子系统,不再需要考虑目标函数或决策变量的处理策略.接着MSO方法与协同进化优化方法比较,它们的共同点都是运用多个种群来模拟演化环境,其区别在于协同进化优化方法是通过竞争或合作关系来实现单个目标或多个目标的优化,而MSO方法是通过迁移算子来实现多个子系统的优化.最后MSO方法与MO–MFEA比较,它们的共同点都是用于优化多系统问题,扩大了智能优化方法的应用范畴;其区别在于MO–MFEA需要对子系统的解空间进行统一编码及目标函数标量化,并在统一的表示空间内进行知识的迁移,MSO方法是通过信息反馈机制,即目标值和约束值的相似程度与解集欧氏距离的折中来实现不同子系统间决策变量的迁移,其演化过程是一种自组织和自学习的动态协调过程.总的来说,MSO方法对各子系统的求解是平行同步优化的,根据问题的耦合性和进化信息的关联性,在一个子系统内部产生的优秀解集,很大程度上也会对其他子系统产生积极的优化效果,因此通过子系统间的迁移,能够加速各子系统的全局优化,从而减少所需的迭代次数,缩短计算时间.

4 实验仿真

为了验证所提的MSO方法的有效性,本节采用文献[19]中的9个基准函数(见表2)进行仿真实验,并分别与文献[16]中的NSGA–II,文献[12]中的MOEA/D和文献[14–15]中的MO–MFEA进行比较,选择这3种算法的原因是前两者是经典的多目标优化方法,后者是目前为数不多且求解多任务性能最好的多因子优化方法.对于表2中的基准函数,其由2个子系统构成,每个子系统包含2到3个目标函数.这些基准函数是根据目标值的相似程度和决策变量的共享程度建立的,其中相似程度分为高(HS)、中(MS)和低(LS),用Sim(T1,T2)来表示子系统T1和T2的相似概率,共享程度分为完全(CI)、部分(PI)和不共享(NI),由此组合构成9个测试函数,这里相似程度和共享程度的分类依据参考文献[19].

表2 多系统(任务)基准函数集Table 2 Multi-system(task)benchmark function sets

便于比较的合理性和公正性,通过多次试验将算法相关参数调节到相对最优来获得合适的性能.对于本文提出的MSO方法,由于其是对基准函数两个子系统同步优化,设置子系统数K=2,每个子种群大小为Ni=100,模拟二进制交叉及pc=1,多项式变异及pm=1,迁移阈值概率pv=1,精英E0=2.对于NSGA–II和MOEA/D,因为两者均为多目标优化算法,因此需要对基准函数中两个子系统单独优化,每次优化的种群大小为N=100,其他参数设置参照MSO方法,另外MOEA/D的分解方式采用边界交叉聚合方法.对于MO–MFEA,由于其整体求解K个子系统,种群大小设置为K·Ni=200,另外其框架是以NSGA–II为基础,因此其他参数设置与NSGA–II相同.所有方法最大迭代次数均为1000,算法独立运行30次,用IGD作为性能衡量指标,其值越小表示性能越好,计算过程参考文献[19],优化结果(IGD平均值和方差)见表3.

表3的结果分两部分讨论:

首先,考虑目标值相似程度对性能的影响,将CIHS,PIHS 和NIHS 作为高相似组(HS 组);CIMS,PIMS 和NIMS 作为中相似组(MS组);CILS,PILS和NILS作为低相似组(LS组).由表可知,对于HS组和MS组,本文所提的MSO方法的性能均优于NSGA–II,MOEA/D和MO–MFEA,对于LS 组,MSO 方法优于NSGA–II和MOEA/D,但在函数CILS和NILS上,劣于MO–MFEA,这表明目标值相似程度对MSO方法的优化性能有很大的影响,基于相似程度来实现子系统间迁移是构建MSO方法的一个重要因子.

其次,考虑决策变量共享程度对性能的影响,将CIHS,CIMS 和CILS 作为完全共享组(CI组);PIHS,PIMS和PILS作为部分共享组(PI组);NIHS,NIMS和NILS作为不共享组(NI组).由表可知,对于CI组和NI组,本文所提的MSO方法的性能均优于NSGA–II和MOEA/D,但在部分函数上则劣于MO–MFEA,对于PI组,MSO方法的性能均优于NSGA–II,MOEA/D和MO–MFEA,这表明决策变量的共享程度对MSO的优化性能也有一定的影响,但规律不是很明显,基于共享程度来实现子系统间迁移是构建MSO方法的另外一个重要因子.

表3 不同优化方法的测试结果比较Table 3 Result comparisons for different optimization methods

综合以上两部分讨论,可以得到MSO方法在相似度高和中的基准函数上比其他方法更具有优势,这也体现了所提方法充分考虑进化信息的继承性和优化环境的关联性,子系统间的迁移能够有效利用这些信息加速全局寻优.

图3 给出了基准函数的Pareto 前沿,以及MSO,NSGA–II,MOEA/D和MO–MFEA在这些函数上的实验结果,从图中可以看到,本文所提的MSO方法在大多数函数上能够接近于理想的Pareto前沿.

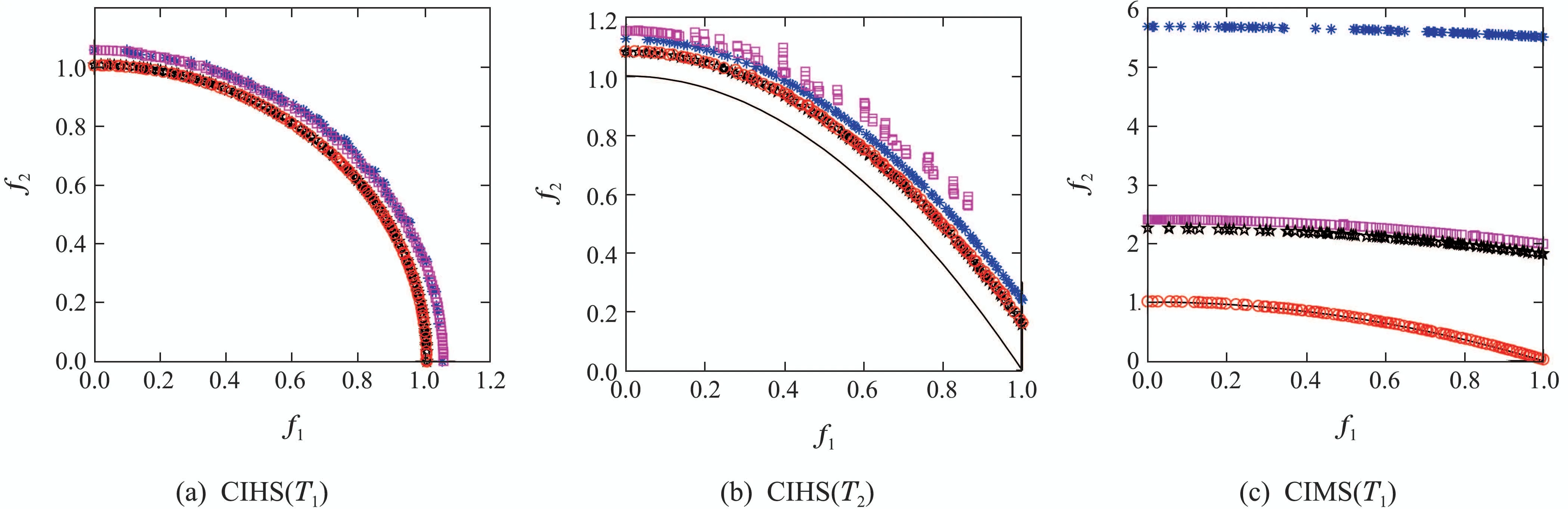
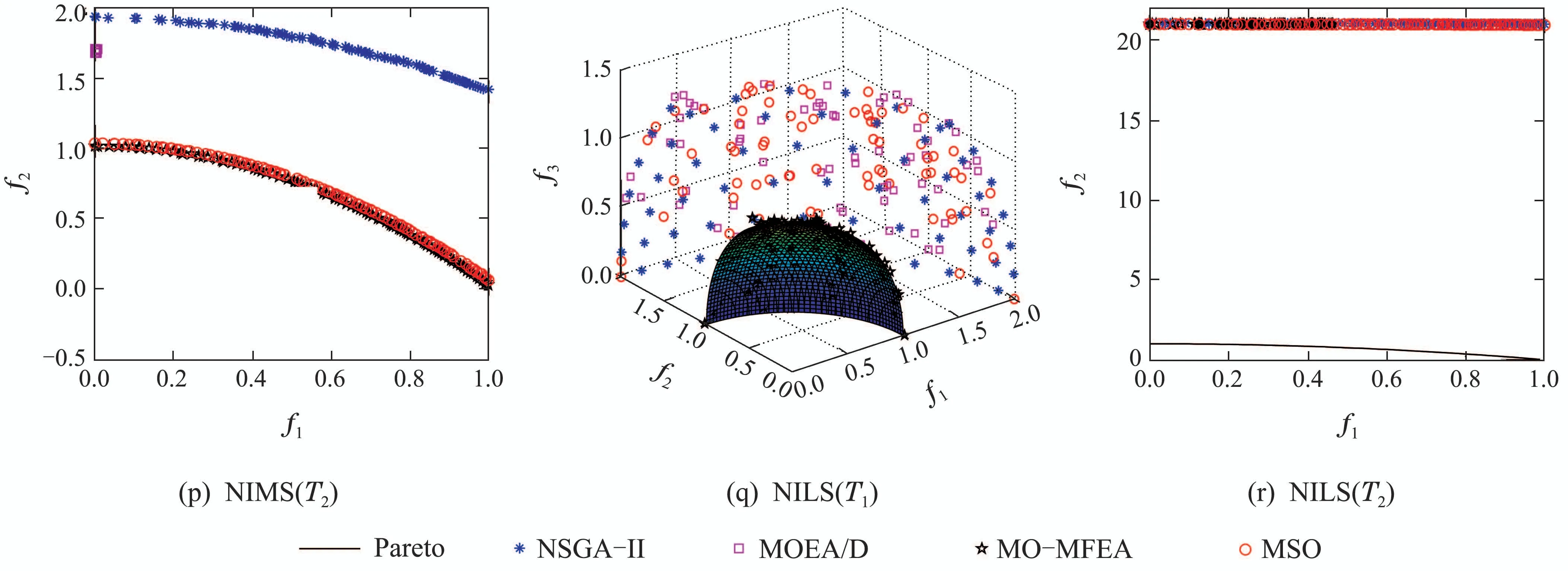
图3 不同优化方法在基准函数上的实验结果图Fig.3 Experimental results of different optimization methods on benchmark functions

5 案例分析

5.1 问题描述

图4为基于多客户按需服务的三级供应链网络,图中制造商A1–AM用于生产不同类型的产品,并将产品运输到不同区域的配送中心C1–CN,然后根据客户需求调用车辆,形成送货路径,并派发至不同客户B1–BL中.从优化的角度分析,该三级供应链网络包括:用于生产制造的多目标车间作业调度子系统、用于产品储存的多目标分配子系统和用于产品派发的多目标旅行商子系统,整个供应链网络构成一个集中决策的多系统优化问题,通过集成优化使得供应链每个子系统的各自效益达到最优,以适应市场竞争.

图4 基于多客户按需服务的三级供应链网络Fig.4 Three-echelon supply chain network based on multi-customer on-demand service

5.2 数学模型

1)对于用于生产制造的多目标作业车间调度子系统,可描述为:存在M个并行独立制造商,每个制造商加工r类产品,每类产品有m道工序,分别在m台机器上加工,产品j在机器k上的加工时间固定,不考虑产品加工的优先权,同一时刻最多只有一个产品在一台机器上加工,且加工过程不会间断,机器间缓冲区容量为无限.设Tij为制造商i中产品j的完工时间,为制造商i中产品j在机器k上的加工费用,所考虑的目标包括最小化子系统内所有产品的最大完工时间和产品的加工总成本,其基本数学模型可描述为

其中每个子目标数学描述如下:

其中:式(12)表示每个制造商中每道工序被加工且只被某台机器加工一次;式(13)表示所有工序的完成时间均为非负值.

2)对于用于产品储存的多目标分配子系统,可描述为:制造商完成不同产品的加工后,需运输到位于不同区域的配送中心,制造商i运往配送中心h的产品种类为cih,对应的运费为,运输流量为wih,所考虑的目标为最小化子系统所有产品的运输总成本和总流量,其基本数学模型可描述为

其中每个子目标数学描述如下:

a)子系统内所有产品的运输总成本

b)子系统内所有产品的运输总流量

该子系统的约束条件为

其中:式(17)表示每个制造商加工的产品种类均为r;式(18)表示每个配送中心的运输量均为非负值.

3)对于用于产品派发的多目标旅行商子系统,可描述为:产品到达不同配送中心后,需要继续将其派发给不同客户,车辆从配送中心h出发遍历Lh个客户后返回到各自所属配送中心(可以看为第Lh+1个客户),设从客户p到客户q的距离为dhpq,费用为,所考虑的目标为最小化子系统内所有产品的派发总路程和总成本,其基本数学模型可描述为

其中每个子目标数学描述如下:

a)子系统内所有产品的派发总路程

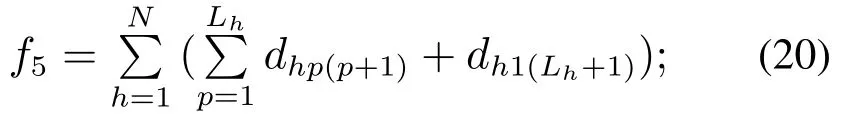
b)子系统内所有产品的派发总成本

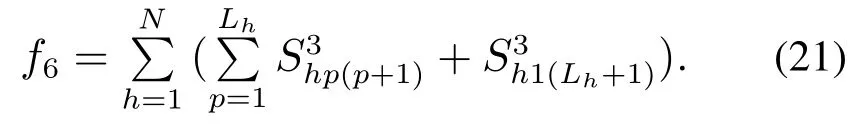
该子系统的约束条件为

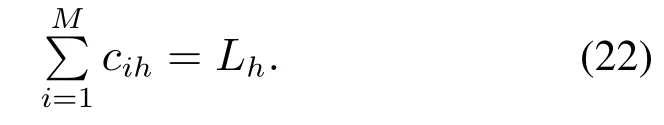
式(22)表示每个配送中心将不同制造商运输过来的所有产品分别派发给Lh个客户.

5.3 仿真结果

采用本文提出的MSO方法求解上述三级供应链网络优化问题.整个供应链网络的参数设置如下:制造商M=5,产品种类r=10,工序m=10,配送中心N=5,客户Lh=9,其他相关数据分别来自JSPLIB[20],QAPLIB[21],TSPLIB[22]数据库;另外系统所涉及的加工费用S1、运输费用S2和派送费用S3服从[1,10]的均匀分布.为了验证所提方法的有效性,同样与NSGA–II,MOEA/D 和MO–MFEA 进行比较,对于MSO 方法,根据供应链网络子系统数,设置子种群数为3,每个子种群的大小为100,对于NSGA–II和MOEA/D,每个子系统单独运行,每次优化的种群大小为100,对于MO–MFEA,种群大小设置为300,所有方法的其他参数与上一节实验仿真中的设置相同,表4给出了作业调度子系统、分配子系统和旅行商子系统的仿真结果,其数值越小表示性能越好.

表4 不同优化方法在供应链网络优化问题上的结果比较Table 4 Result comparisons of different optimization methods for supply chain network

从表4中可以观察到,本文提出的MSO方法在求解三级供应链网络优化问题上,对于其中的车间作业调度子系统,其性能略优于NSGA–II和MOEA/D,与MO–MFEA基本相同,这是因为车间作业调度子系统模型跟其它两个子系统模型相比,交互较少,可以看作为一个相对独立的多目标优化问题,这对于本文提出的MSO方法而言,难以发挥子系统之间的迁移操作优势,在这种情况下,其退化为改进版的NSGA–II,因此MSO方法在该子系统上难以呈现出性能优势.而对于分配子系统和旅行商子系统,MSO方法的性能要远好于NSGA–II和MOEA/D,略优于MO–MFEA,这是因为这两个子系统与车间作业调度子系统相比,其模型表达式和约束更为相似,变量之间的关联也更为密切,因此本文提出的MSO方法在不需要先验信息的情况下,能够通过其自身的优化机理求解问题,并呈现出好的优化潜力.

6 结论

人工智能的快速发展引发了新一轮产业升级和变革,同时也涌现出大量具有多系统多目标特点的复杂耦合问题.为解决这些优化问题,本文提出了一种MSO新方法,其借鉴多种群进化算法的智能平行特征,利用在一个子系统内部产生的优秀解集通过迁移来帮助和启发其他子系统的进化,从而加速整个问题的全局优化.同时,为测试新方法的可行性和有效性,将该方法应用到基准函数和具有多系统优化特征的三级供应链网络,仿真实验结果表明新方法在基准函数和应用问题上均具有很好的整体优化能力,为解决其他复杂耦合优化问题提供了新的思路和较强的参考意义.未来的研究方向一方面从剖析复杂耦合问题内在关系,考虑不同子系统间的异质结构和求解策略,来建立更准确的多系统优化模型;另一方面在目前的MSO方法框架下,根据问题支撑条件改进算子结构提高优化性能,并力图求解产业变革中所涉及的各类复杂耦合问题.