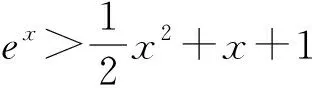提取结论 妙证不等式*
——谈高中数学课堂教学中发展学生逻辑推理素养
福建厦门外国语学校石狮分校 (362700) 石明荣
“逻辑推理”是指从一些事实和命题出发,依据规则推出其他命题的素养.是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.在高中数学课堂教学中,如何发展学生“逻辑推理”素养,关键在于如何引导学生发现问题和提出问题,然后利用所学知识进行表述和论证,形成有论据、有条理、合乎逻辑的思维品质和理性精神.笔者就如何在高中数学课堂教学环节,通过对几个常见结论的证明和提取,进一步解决一类数学试题,发展学生的“逻辑推理”素养,拓展学生的解题思维能力,仅供同仁参考.
1 发现问题,提取结论,提升思维品质
例1 (人民教育出版社(A版)数学(选修2-2)第32页,习题1.3B组第1题)利用函数的单调性,证明下列不等式,并通过函数图象直观验证:
(1)sinx
证明:(1)设f(x)=sinx-x,x∈(0,π),则f′(x)=cosx-1<0,所以f(x)在(0,π)上为减函数,从而f(x) 图1 如图1可知,当x∈(0,π)时,函数y=sinx的图象在函数y=x的图象的下方,从而当x∈(0,π)时,不等式sinx (2)设f(x)=ex-(1+x),则f′(x)=ex-1.当x<0时,ex<1,f′(x)<0,所以f(x)在(-∞,0)上为减函数.当x>0时,ex>1,f′(x)>0,所以f(x)在(0,+∞)上为增函数.从而f(x)≥f(0)=e0-1=0,当x≠0时,f(x)>0,不等式ex>1+x成立. 图2 如图2可知,当x≠0时,函数y=ex的图象在函数y=1+x的图象的上方,从而当x≠0时,不等式ex>1+x成立. 通过对以上两道课本习题的证明,学生容易发现问题,进一步提取出如下结论: 结论1当x≥0时,sinx≤x; 结论2当x∈R时,ex≥1+x; 通过对以上两道试题的证明,再次引导学生可以发现问题,容易提取到如下结论: 借助以上四个结论,可以快速解决部分与ex,lnx,sinx,cosx有关的不等式试题,达到事半功倍之效果,从而发展学生的“逻辑推理”素养,拓展解题思维能力. 例3证明下列不等式:(1)ex+cosx-3>lnx;(2)ex+cosx-1>xlnx. 例4任意x∈[0,+∞),不等式eax+cosx-sinx≥2恒成立.求实数a的取值范围. 分析:不等式eax+cosx-sinx≥2中既有指数式,又有三角函数式,若能把三角函数化为多项式结构,结合上述结论,容易求得实数a的取值范围. 综上所述,教师通过引导学生挖掘“教材中的习题”,鼓励学生大胆发现、猜测,进一步提取出一些结论,根据所提取的结论,大胆地去尝试解题,从而发展了“逻辑推理”核心素养,拓展了逻辑推理能力.广大教师应尽力构建以核心素养为导向的数学课堂,将核心素养的培养渗透到数学的每一个环节,实现“素养型”课堂的转型.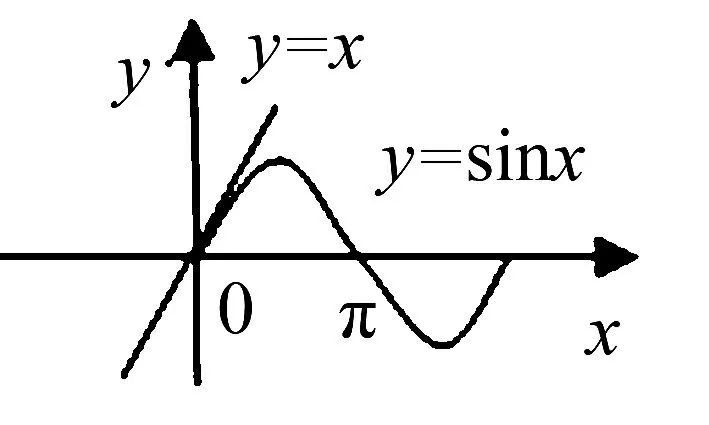

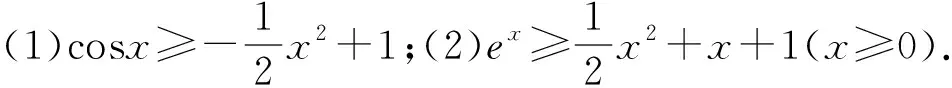


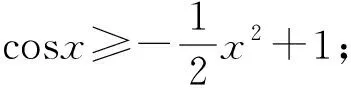
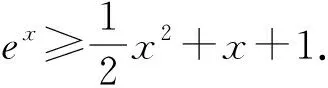
2 解决问题,发展学生“逻辑推理”素养,拓展学生解题思维能力