高三数学课堂的高效源于“用教材教”*
——例谈改编教材例习题的几种手段
江苏省江浦高级中学 (211800) 徐爱勇
纵观近些年高考卷,每年试题中总会有相当一部分直接来源于教材例习题的改编、拓展、整合,有些试题甚至就是教材的原题.这一举措对推进课程改革起到了良好的“风向标”作用,同时还能够更加理性地引导教师在教学过程中要重视教材的使用,注重挖掘教材的内涵.“用教材教”这一观点应当成为全体一线教师达成的一条基本共识.“用教材教,而不是教教材”真正的意图是要求教师能够更加灵活地、富有创造性地使用教材.如果把教材文本呈现的内容看作是“露出海面的冰山一角”,那么“用教材教”就要求教师能够把“海面以下的巨大冰山托出海面”,让学生领略到“整座冰山”.
高效课堂是学生主动学习、积极思考的课堂,是师生互动、生生互动的课堂,是学生对所学知识主动实现意义建构的课堂.构建高效课堂业已成为全体同仁不懈的追求.基于此,笔者试结合自身的教学经验和体会,来阐述在高三复习过程中,改编教材例习题的几种手段,以期能够达到高效备考的目的,希望能够引起广泛地关注.
1.手段1——变换图形
案例1(苏教版数学2 P95第21题)已知M(-1,3),N(6,2),点P在x轴上,且使PM+PN取最小值,求点P的坐标.
变式平面直角坐标系中,点A(1,-2),B(4,0),P(a,1),N(a+1,1),当四边形PABN的周长最小时,过三点A,P,N的圆的圆心坐标是.
评析:本题主要考查的核心知识点为“求点关于线的对称点”.更多时候,对其变式多为“改变对称轴的位置”,从而增加其运算的容量.更有甚者,将对称轴直线的斜率定为1或-1,从而直接得出结果,将解题思索过程固化,偏离了解题教学的价值方向.
改变已有命题的条件或结论的表现形式,将原命题中的条件或结论间接化、隐蔽化,或改变问题的背景变换出新的命题的方法.本题变式的核心就是“将线段BN平移至PC,其中C(3,0)”即可,从而体现其“灵动性”.
2.手段2——以图思题
案例4(苏教版必修4P122例5图3-2-2)如图1,在半圆钢板上截取一块矩形材料,怎样截取能使这个矩形的面积最大?

图1

图2
变式(1)(苏教版必修4 P121思考)在一个圆所有内接矩形中,怎样的矩形面积最大?
(2)(苏教版必修4 P132 第18题)如图2,在半径为R,圆心角为60°的扇形AB弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点M,N在OB上,求这个矩形面积的最大值及相应的∠AOP的值.

图3
(3)(苏教版数学5 P19例4)如图3,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,问:点B在什么位置是,四边形OACB的面积最大?
(4)在(3)的基础上,点B在什么位置时,线段OC的长取最大值?
评析:通过归纳类比、拓展思考、反思建构,做到举一反三,由此及类,由习题到模式,这是培养解题能力、抽象概括能力的重要手段.本组题在教材中均为核心题型,按照如此串联和变式,圆→半圆→扇形→矩形→三角形→面积→长度→……一目了然,从而增强了复习的针对性.
3.手段3——变量包装
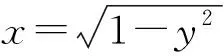
变式(1)已知u≥1,v≥1且(logau)2+(logav)2=loga(au2)+loga(av2)(a>1),则loga(uv)的最大值为,最小值为.
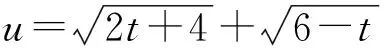

评析:有些问题看似平淡无奇,缺乏新意,但若我们对问题进行改头换面,或提炼,或抽象,或纯化,往往会有意想不到的感悟.这些感悟主要是把一个个零散的发现由表及里、由浅入深地集中和联系起来,再通过恰当的方法加以处理,化归为已有的认识,就自然形成了构造模型的方法,这一构造思想一般超越了问题的原有意境,具有更为丰富的想象力和创造力.
4.手段4——直观想象
案例4(苏教版数学5 P56第6题)设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,求证:a2,a8,a5也成等差数列.
变式(1)设Sn是等比数列{an}的前n项和,a2,a8,a5成等差数列,求证:S3,S9,S6也成等差数列.
(2)设Sn是等比数列{an}的前n项和,S4,S10,S7成等差数列,求证:a3,a9,a6也成等差数列.
评析:有些数学问题的已知条件或结论的外表形态与结构,让人容易想到相关的或相似的定义、定理、公式或图形等,如果我们善于抓住这一直觉,也许会从中得到有益启发.当我们解完题后,一个很自然的念头,立即会从脑海中掠过.该问题的逆命题是否成立?显然成立,解答过程从略.
再审视本题,还可以发现条件和结论之间的下标似乎存在某种对应关系.经过持续探究,可得到如下结论:设Sn是等比数列{an}的前n项和,Sm,Sn,St成等差数列,求证:对任意自然数k,am+k,an+k,at+k也成等差数列.
5.手段5——横向到边
案例5(苏教版数学1 P73第5题)汽车在隧道内行驶时,安全车距d(m)正比于车速v(km/h)的平方与车身长(m)的积,且安全车距不得小于半个车身长.假定车身长约为4m,车速为60km/h,安全车距为1.44个车身长.(1)试写出车距d与车速v之间的函数关系式;(苏教版选修2—2P38页第4题,题目同上,增加了第2问)(2)在交通繁忙时,应规定怎样的车速,可以使隧道的车流量最大?
变式将上两题进行整合,合并成一题,从而完成从“建模”到“解模”完的整过程.
评析:对数学习题的拓展常表现在解题方法层面上.这是一种联系性拓展,但数学教学中的联系性拓展不仅局限于此,还包括对教学内容之间的前后串联、课本例题的深化引申、课后习题的整合统一等.
不同的数学分支间具有普遍的联系性,有的显而易见,有的则较为隐蔽.数学教学的一个功能就是要向学生揭示这种关系,在这个过程中,可以使学生的知识体系得到整合,并逐渐对数学中的各种思想方法产生较为清晰的认识.
6.手段6——纵向到底
案例6(苏教版数学1 P8例1)写出集合{a,b}的所有子集.
(苏教版数学1 P9练习1)写出集合{1,2,3}的所有子集.
(苏教版数学1 P8旁白)集合{a1,a2,a3,a4}有多少个子集?
(苏教版数学1 P17第8题)求满足{1,3}∪A={1,3,5}的集合A.
(苏教版数学1 P94第18题)已知一个函数的解析式为y=x2,它的值域是{1,4},求此函数的定义域.
变式(1)集合{a1,a2,…,an}的所有子集的个数是多少?
(2)求集合M={1,2,3}的所有非空子集中各元素之和.若M={1,2,3,4}呢?你能按此方法大胆尝试探索,发现一个具有一般规律的结论吗?
(3)若A∪B={a,b},则这样的A,B共有多少组?若A∪B={a,b,c},则结论又如何呢?若A∪B∪C={a,b},则结论又如何呢?你能按此方法大胆尝试探索,发现一个具有一般规律的结论吗?
评析:我们把表面上不尽相同,而问题实质一致的若干问题有机地衔接在一起,形成问题串的方法.这种方法体现了在知识交汇点处命题的指导思想,也是各级各类考试中命制习题最常用的方法.
数学教学不仅要让学生掌握一定的数学知识,更重要的是要让学生理解蕴涵在这些知识中的丰富数学思想.数学思想方法对学生思考问题、解决问题更具有普遍性与指导性.例习题的教育价值是否能够充分发挥出来,完全取决于例习题中的数学思想是否被我们充分地挖掘与展现.
类似的题目和手段还可以举出一些.但本文的目的不是针对个别的题目,而是想纠正目前高三数学复习环节中的一些不良倾向.在高考复习中“用教材教”,以主干知识为核心,以教材例习题的拓展性、多解性、归一性、开放性和辨析性等特点精心做好高三数学复习工作,积极更新教学观念,只有这样才能真正地做到回到课本中去.

