深度迭代卷积神经网络的快速脑部MRI重建算法*

杜年茂，宋 威

江南大学人工智能与计算机学院，江苏无锡214122

1 引言

核磁共振成像（magnetic resonance imaging，MRI）是一种重要的医学成像手段。MRI具有无辐射、对比度高、多模态的特点，被广泛应用于脑部疾病检查。然而MRI成像时间较长，通常需要30 min[1]。长时间的数据采集会导致患者身体不舒服（肢体运动或幽闭恐惧症等），进而引发运动伪影。此外成像时间过长也是MRI诊断价格昂贵的原因之一。因此缩短MRI成像时间有很大的临床诊断意义与经济意义。

MRI成像时间长的主要原因在于原始数据只能依次于k-空间（图像的傅里叶空间）中采集，然而k-空间的遍历速度受基础MR物理学的限制（如T1、T2的TR值分别为800 ms与2 000 ms）[2-3]。除了物理硬件上的改善外，一个直接有效的加速MRI成像的措施为k-空间欠采样。在理论上，k-空间欠采样能够提供相应比例的加速度。然而，k-空间欠采样违反了Nyquist-Shannon采样定律，并且会在重建图像中生成严重的混叠伪影，严重程度与欠采样倍数正相关。欠采样的MRI重建的主要挑战在于利用MRI数据的先验知识来补偿丢失的数据。

传统的欠采样MRI重建算法主要是基于压缩感知（compressed sensing，CS）理论[4]，即CS-MRI[5]。基于CS理论MRI图像可以低于Nyquist Shannon采样频率进行采样，前提如下：（1）数据是可压缩的，即在某个变换域具有稀疏表示；（2）数据采样是非相干的。在这两个前提下可以通过非线性优化或者迭代算法进行重建[6-7]。早期的CS-MRI主要利用MRI在特定域的稀疏性，如全变分（total variation，TV）[5,8]与小波变换域等[9-10]。这些方法相对简单快速，但是会在重建图像中引入阶梯伪影[3,11]。此类方法的自然拓展是通过自适应的建模以实现更加灵活的稀疏域表示。其中比较有代表性的算法是字典学习方法[12-13]。字典学习方法依靠构建局部块字典来提高重建精度。由于字典是从数据中学习的，因此字典学习方法能够重建出更高质量的图像。但是字典学习方法也有重建时间长以及正则化方程和超参数选择困难的问题[2,14]。

与传统方法相对的是，近年来深度学习方法尤其是卷积神经网络已经被成功应用于欠采样的核磁共振图像重建。不同于传统的手工提取特征的方式，深度网络通过训练可以学习到更抽象的数据表示。现有的研究已经证明基于深度学习方法在重建精度以及速度上超越传统的基于CS的方法。如Schlemper等[15]提出了深度级联神经网络，将传统的迭代优化问题展开为深层级联网络，并使用数据一致性（data consistency，DC）模块来保障数据的保真度，该方法在重建精度和速度上均超过经典的字典学习方法。Yang等[2]提出了一种深度去混叠生成性对抗网络（deep de-aliasing generative adversarial networks，DAGAN），该网络使用残差U-net作为生成器，并结合了图像域、频域、感知和对抗信息作为损失函数。Yang等[2]与传统的算法进行了丰富的对比实验，其方法在重建精度和速度上也超过传统方法。最近Wang等[16]提出了复数卷积神经网络，该网络使用了复数卷积核来处理复数数据。除了图像域的卷积，Eo等[3]与Souza等[17]研究了混合域卷积神经网络，即在图像域与k-空间混合卷积。

为了达到更大的加速因子，可以考虑如下两种策略：一种是利用MR数据自身的冗余性，如MRI切片内部的冗余。二是当成像场景为3D模式时，可以利用相邻切片间的冗余关系。人体脑部MRI图像通常是序列的，相邻切片间存在着数据冗余。上述基于深度学习的方法对比于传统方法都取得了显著效果，但是这些方法都只针对单幅MRI图像进行重建，没有利用相邻切片间的数据冗余。针对此问题，本文提出了一个深度迭代卷积神经网络（deep iterative convolutional neural network，DICNN）。该网络主要包含两部分：第一部分是双向卷积（bi-directional convolution，BDC）模块，用于处理切片间的数据冗余关系；第二部分是精细化网络（refine net，RNET），用于处理单个切片内部的冗余关系。本文依次迭代使用BDC与RNET对欠采样的MRI进行端到端的训练，以达到更大的加速因子以及更好的重建质量。

2 相关研究

2.1 循环神经网络

循环神经网络[18]（recurrent neural network，RNN）是一种以序列数据作为输入的神经网络，它在序列演化的方向上是递归的。RNN具有记忆能力，因此在学习序列的非线性特征方面具有优势。对于图像序列，RNN也有很好的序列建模能力，比如RNN已经被成功应用于3D医学图像分割领域[19-21]。通过在RNN递归过程中使用卷积操作融合相邻切片，使来自先前切片的信息可以有效地流入后续切片中。Schlemper等[14]使用双向卷积网络用于动态MRI重建，并取得了成功。由于人体脑部MRI图像序列相邻切片间也存在着关联，本文基于RNN的特性构造了BDC模块来处理切片间的数据冗余。

2.2 数据一致性

DC模块的作用是保持数据在k-空间的保真度。其原理是，MR信号采集自k-空间，欠采样的MRI只收集了部分k-空间数据，那么重建算法在恢复图像时应该被限制修改这部分已知的数据。原始k-空间数据经过逆傅里叶变换得到可视化的MRI图像，对重建后的图像进行傅里叶变换可以得到其在k-空间的表示。对于基于图像域的重建算法而言，对重建图像经过傅里叶变换，再用原始的k-空间信号替换掉重建的k-空间信号便可以达到数据一致性的效果。DC模块的定义如下：

2.3 注意力机制

注意力机制在很多计算机视觉的任务中被证明是有效的[22-24]。如在可变形卷积[25]的研究中，通过学习热力图来为特征赋予权重。Zhang等[26]通过添加长跳跃连接（long skip connection，LSC）来使网络专注于高频信息的学习。在欠采样的MRI重建中，通常需要保持一定比例的低频数据来维持图像的基础结构，大量包含组织细节的高频信息丢失。受到文献[26]的启发，本文在BDC与RNET中使用LSC。

3 方法

3.1 核磁共振成像原理与过程

核磁共振成像，是利用核磁共振（nuclear magnetic resonance）原理，通过外加梯度磁场以一定的频率（拉莫尔振动频率）向物体中注入能量，然后测量能量在物体内部不同结构环境中不同的衰减时间，即可获取构成这一物体的原子核的位置和种类，据此可以绘制成物体内部的结构图像。由于磁场对人体是无伤害的，因此核磁共振成像是非侵入的[27]。

核磁共振成像空间为k-空间，填充k-空间的数据直接从MR信号中获取。因为使用频率、相位与梯度磁场来对空间进行定位，所以MR信号已经具有适合于填充k-空间矩阵的类傅里叶格式。对获取的k-空间数据进行逆傅里叶变换就能得到MR图像。图1展示了一幅核磁共振图像在k-空间与图像域之间的相互转换关系。

Fig.1 Visualization of k-space and image domain of MR images图1 核磁共振图像的k-空间与图像域的可视化

从图1中可以看出，k-空间数据通常是排列在矩形格子中，与空间域图像的大小相同。但是kx和ky轴表示的是二维傅里叶空间中的频率，而不是图像域的x和y轴上的像素点。k-空间数据与图像域数据并不是一一对应的，k-空间的每一个数据都包含最终MR图像中所有像素点的空间频率信息与相位信息。反过来图像域的每个像素点都能映射到k-空间数据中的所有数据。图1中的箭头很好地展示了这一原理。

MR图像数据采集的过程可以用下列公式描述：其中，y表示k-空间的观测矩阵，x表示图像域的数据。

3.2 问题建模

设x∈ℂD为需要重建的复数值的脑部MR图像序列。D=DxDyT，其中Dx与Dy分别为MR图像的宽与高，T表示序列长度。设y∈ℂM表示欠采样的k-空间观测矩阵。重建问题就是从部分采样数据y中重建出x：

其中，ε是噪声项，Fu是欠采样的傅里叶编码矩阵。由于在欠采样的模式下，M≪D，这使得式（3）的逆问题成为病态问题。通常情况下，该类问题能以非限制优化问题加以解决：

对于传统的基于CS的方法，R通常为x在特定变换域的l0或l1范式，λ为噪声系数。基于深度学习的研究将卷积神经网络作为额外的约束项整合到基于CS的重建方法中：

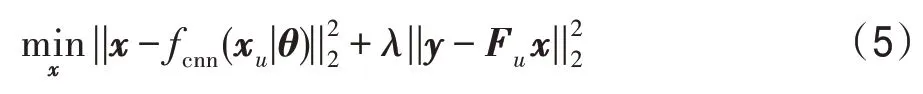
其中，fcnn表示卷积神经网络，θ是网络参数。fcnn以零填充的重建图像作为输入，然后直接产生重建图像作为输出。通过这种方式，施加在x上的正则化项可以近似地由卷积神经网络来表示。由于低于Nyquist采样频率，xu中的混叠伪影十分严重，因此基于卷积神经网络的重建方法可以视为图像域的去混叠问题。

3.3 基于DICNN的快速脑部MRI重建算法

本文分别使用两个独立的模块来分别利用脑部MRI序列两方面的冗余。其中BDC模块用于切片间的冗余关系，RNET用于切片内的冗余关系。本文提出的网络整体结构图如图2所示。DICNN以迭代的方式对脑部MRI图像序列进行重建。初始时，DICNN以零填充重建图像x0与其在k-空间的观测矩阵y作为输入，其中x0=xu。经过N次迭代后输出重建结果xN：

Fig.2 Overall network structure of DICNN图2 DICNN网络整体结构图

其中，θj,j∈[1,2,…,N]是每个迭代阶段卷积神经网络fcnn的参数。理论上可以共享权重。

在每次迭代中，先使用BDC提取相邻切片间关系：

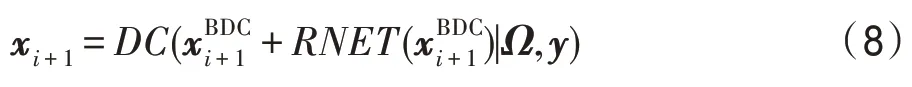
BDC是一个双向卷积神经网络，RNN的结构使得BDC能够有效地对脑部MRI序列进行建模。BDC的网络结构如图3所示。因为BDC模块可以视作一个重建子网络，可以输出重建结果，为了简单起见，设表示第i+1次迭代中BDC网络的输入，表示相对应的输出项。图3中蓝色节点表示MRI切片，绿色节点表示隐藏层特征，箭头表示相应的节点的数据流动方向。

Fig.3 Network structure of BDC图3 BDC网络结构图

BDC模块在一个方向递归过程可以用如下过程公式表示：

相似的，BDC模块在另一个方向上的递归过程如下：

在式（9）与式（10）中，h是隐藏层特征，其上的箭头表示循环卷积神经网络的递归方向，[:]表示拼接操作，f表示2D卷积操作。最后对两个方向的重建结果融合得到第i+1次迭代中BDC模块的重建结果：

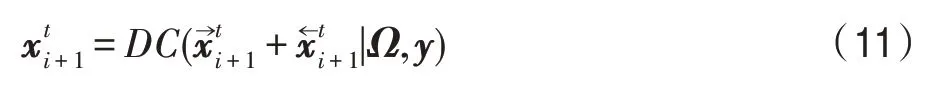
RNET是由d个堆叠的2D卷积操作组成，如图1中RNET放大部分所示。其中表示第i次迭代RNET中的第k个2D卷积核，k∈[1,2,…,d]。堆叠的卷积操作能够有效地扩充RNET在二维平面内的感受野，从而去除局部地区的混叠伪影。

4 实验与结果分析

4.1 实验数据

本文实验使用的是Calgary-Campinas数据（https://sites.google.com/view/calgary-campinas-dataset/home）。该数据集公开了35个T1加权单线圈脑部MRI样本。数据成像方向为矢状方向，单个样本的序列长度170，每张图片的大小为256×256，切片厚度为1 mm。以下实验若无特别说明，均采用的是三折交叉验证，其中两折训练集大小为23，测试集为12，最后一折训练集大小为24，测试集为11。

4.2 欠采样模式

为了验证本文算法的性能，主要使用了在快速核磁共振成像研究中常用的四种欠采样模式。它们分别是：Cartesian欠采样、Spiral欠采样、Radial欠采样与Poisson欠采样。这四种欠采样模式如图4所示。

其中Cartesian采样轨迹由于其硬件设计简单，容易实施，被广泛应用于现代商用MRI仪器。因此本文研究主要以此欠采样模式为主。由于MRI成像时在频率方向编码速度远快于相位方向的编码速度，因此在进行欠采样时通常会省略相位方向的数据。如图4（b）、（c）所示，本文使用了两种欠采样因子，分别为4倍和6倍。在欠采样时，需要保留一定比例的低频数据（autocalibration lines，ACL）用于维持图像的基础结构。本文在两种加速模式下分别保留了8%和6%的ACL。

对于Cartesian欠采样模式，本文使用了文献[15]中变密度随机欠采样的方法，除了ACL保持固定，对剩余的数据进行随机采样。该采样方法的实现在文献[15]公开的源码连接中找到。采样mask为在线生成，并且对于每张切片都随机生成采样mask。这样不仅会增强MRI数据的非相干性，而且能在训练时起到数据增强的效果。为了应对随机采样造成每次测试结果的不同，在测试时根据文件名称固定了随机数种子，以确保每种算法在测试时使用的是相同的欠采样mask。

除了Cartesian欠采样模式外，本文还探究不同欠采样模式对于重建质量的影响。主要设计了6倍欠采样模式下的另外三种欠采样mask，它们分别是Radial欠采样[28]、Spiral欠采样[29]与Poisson欠采样[30]。三种欠采样mask与其对应的零填充重建图如图4（d）、（e）、（f）所示。从图3中可以看出，不同的采样轨迹其重建伪影也有不同的特点，与Cartesian欠采样mask相比，Radial欠采样模式下出现了弧状的混叠伪影，Spiral欠采样模式下出现了波纹状的混叠伪影，Poisson欠采样模式下的伪影呈斑驳状。对于这三种欠采样模式mask的生成采用的线下模式，采样轨迹生成方程使用的是基于Python的sigpy工具包，网址为https://sigpy.readthedocs.io/en/latest/mri.html。

Fig.4 Visualization of k-space data and reconstructed image in undersampling modes图4 欠采样模式下k-空间与重建图像的可视化

4.3 评价指标

本文采用三种通用的图像质量评价指标，它们分别是归一化均方误差（normalized mean square error，NMSE）、峰值信噪比（peak signal to noise ratio，PSNR）与结构相似度（structural similarity，SSIM）。NMSE越小越好；PSNR单位为dB，其在数值上越大表明重建结果越好；SSIM数据值接近1说明图像结构相似，重建结果越好。NMSE和PSNR是基于误差敏感的图像质量评价，强调整体重建精度；SSIM强调图像质量的感知。

4.4 实验环境与参数设置

本文网络代码实现是基于Pytorch 1.1.0版本。实验环境为Google Colab，显卡型号为Tesla P100，显存16 GB，CPU型号为Intel®Xeon®CPU@2.20 GHz，内存大小为26 GB。

DICNN网络参数设置如下：网络总的迭代次数设置为I=5，RNET中卷积层数d=5。网络中卷积核大小为3，步长为1，为了保持图像大小，padding值设置为1。除输入输出层外，卷积层通道数为64。由于采集到的MRI信号值为复数，因此本文将输入层与输出层通道数为2，分别存储复数的实部于虚部。激活函数采用Leaky ReLU，其中α值设置为0.1。网络的训练采用Adam优化器，初始学习率为e=10-3，训练轮次为200轮，并且在训练170轮次后e衰减至10-4。由于使用的数据集单个MRI序列为170，直接放入网络会造成显存负担，故本文在训练时随机从序列中截取长度为s=16的序列进行训练。由于子序列是随机截取的，因此在训练过程中也起到了数据增强的效果。本文在测试时使用了完整的序列长度，4.6节进一步探索了测试时序列长度对于模型精度的影响。

4.5 BDC与RNET

为了验证BDC与RNET两个模块的性能，本文对这两个模块进行了消融实验。主要进行了四个实验：（1）BDC，即仅使用BDC模块；（2）RNET，同上；（3）RNET-BDC，在每次迭代中先使用RNET，后使用BDC，即先处理MRI切片内部的冗余关系，后处理MRI切片间存在的冗余关系；（4）DICNN，即本文所提出的最终的模型。其中实验（1）和（2）探索单个模块的性能。实验（3）和（4）探索的是模块顺序对于重建结果的影响。

本部分实验采用三折交叉验证，欠采样因子为6。为了简化实验过程，本节所有模型的训练轮次为100，学习率衰减的训练轮次数为第80轮，实验结果如表1所示。

Table 1 Comparison of reconstruction accuracy of DICNN structure variations表1 DICNN结构变体重建精度的比较

从表1的实验结果可以看出，BDC与RNET的重建精度相近。RNET-BDC与DICNN的重建精度与上述两者差距较为明显。这进一步说明利用MRI序列中切片间的数据冗余有助于提升重建精度。RNETBDC与DICNN的对比结果表明，先使用BDC模块，后使用RNET模块是最优的网络结构。

4.6 测试序列长度对重建精度的影响

为了验证测试时的序列长度对重建结果的影响，本文对6倍Cartesian欠采样模式训练出来的模型进行了如下实验。即在测试时使用不同的序列长度，测试子序列长度从16开始，以步长为16递增。三折交叉验证的实验结果如图5所示。

Fig.5 Reconstruction results of using different sequence lengths during testing图5 测试时使用不同序列长度的重建结果

可以看到随着测试时序列长度的增加，重建精度总体呈现上升趋势。在本文中，当测试时序列长度设置为96时重建结果最优。但是，同样需要注意的是，切片长度为96的重建结果比切片长度为16的重建结果的PSNR值提升是在千分位级别。这说明本文方法在测试时的序列长度上有很强的鲁棒性。这一结果同时也凸显出本文提出网络结构的有效性，即在循环迭代的过程中能够有效地处理相邻切片间的数据冗余，不会因序列长度变化而显现性能上的大幅度变动。

4.7 与其他方法的比较

为了验证所提出算法的有效性，实验使用深度级联卷积神经网络（deep cascade of convolutional neural networks，DC-CNN）[15]、混合卷积神经网络（hybrid,dual domain，cascade of convolutional neural networks，H-CNN）算法[17]和卷积循环神经网络（convolutional recurrent neural networks，CRNN）算法[14]进行比较。其中DC-CNN是基于深度学习的迭代重建算法，HCNN是基于k-空间与图像域的混合卷积神经网络。这两个算法基于单幅MRI切片的重建算法，没有使用相邻切片间的数据冗余关系。CRNN与本文的DICNN是基于MRI序列的重建算法。表2显示了不同算法在不同欠采样模式下的三折交叉验证结果。

从表2中数据可以看出，DICNN在不同采样模式下的所有重建指标均优于其他对比方法。此外还可以从表2中分析出，脑部MRI序列中相邻切片间的数据冗余有助于提升重建质量。例如，在4倍欠采样Cartesian模式下DICNN的PSNR值比DC-CNN高1.85 dB，然而在6倍Cartesian欠采样模式下这一差距变成了2.97 dB。同样的，CRNN在4倍模式下的重建精度与DC-CNN相当，但是在6倍模式下重建精度明显高于DC-CNN，为1.53 dB。同样都利用了切片间的数据冗余，DICCN在两种欠采样模式下的PSNR值分别比CRNN高出1.42 dB与1.44 dB。这表明DICNN在提取MRI序列中数据冗余的能力更强。

此外表2中还包含了各方法在另外三种欠采样模式的重建结果。相较于6倍Cartesian欠采样模式，各方法在6倍Radial、Spiral与Poisson欠采样模式下的重建精度有明显提高。

图6显示了6倍Cartesian欠采样模式下，四种重建算法在不同切片上的重建结果。对于每个切片编号，其PSNR值为三折交叉实验结果的平均。从图6中可以看出，MRI序列两端的重建精度很低，这是因为本文所选用的脑部MRI数据集的成像方向为矢状方向，序列两端的图像包含人体组织很少，因此信噪比较高。此外每个算法的PSNR曲线均呈盆地状，中间切片的精度较低。DICNN相较于其他重建算法PSNR曲线更高，且更加平坦。

Table 2 Reconstruction accuracy of different methods under different undersampling methods表2 不同欠采样下不同方法的重建精度

Fig.6 PSNR values of different reconstruction algorithms on different slices图6 不同重建算法在不同切片上PSNR值

Fig.7 Comparison of reconstruction results of different algorithms under different undersampling modes图7 不同算法在不同欠采样模式下的重建结果比较

为了从主观上体现重建算法的区别，图7比较了四种算法在6倍Cartesian、Radial、Spiral与Poisson欠采样模式下的重建结果。从重建图像上可以看出，6倍Cartesian欠采样模式下，H-CNN与DC-CNN丢失了大量的脑部组织细节，如小脑区域。CRNN在此欠采样模式下能够恢复出部分细节，但是不够理想。与CRNN相比，DICNN能够提供更多更清晰的边缘细节。从图7中的绝对值误差图上可以看出，DCCNN与H-CNN的重建出现较高的误差，相比较下CRNN与DICNN的误差图不明显。此外，从图7中6倍Cartesian欠采样模式下误差图下的刻度条上也能看出DICNN的误差峰值比其他算法小。图8显示了6倍Cartesian欠采样模式下各方法重建图像在小脑区域的放大图。可以看到，H-CNN与DC-CNN重建的图像在细节纹理上十分模糊。虽然在6倍欠采样因子下CRNN的重建指标高于H-CNN与DC-CNN，但是重建图像依然模糊，细节丢失严重。通过对比可以看出，DICNN的重建图像更接近真实图像。

Fig.8 Comparison of details under 6X Cartesian undersampling mode图8 6倍Cartesian欠采样模式下的重建细节比较

图7中还展示了四种算法在6倍Radial、Spiral与Poisson欠采样模式下重建结果与真实图像的误差图。从误差图的彩色条上的刻度线可以看出，各种方法的重建可视化结果与表2中数据一致。在6倍Spiral欠采样模式下，各方法的重建质量要低于6倍的Radial与Poisson欠采样模式，这一点也可以从误差图中的刻度线上看出。

为了进一步探索本文所提方法在四种欠采样模式下的重建效果，图9显示了6倍欠采样模式下，DICNN在四种欠采样模式下的重建结果。图9中第二行分别使用绿、黄、红三色箭头指出了四种欠采样模式重建图像中的小脑区域的三处边缘细节。可以看到虽然DICNN在Poisson欠采样模式下获得的重建精度最高，但是在重建图像上的部分细节上不如其他降采样模式清晰，如图9中的黄色箭头所指。从视觉效果来看，Radial降采样模式重建出来的图像细节更加丰富，更接近真实图像。在表2中，DICNN在6倍Cartesian与6倍Spiral欠采样模式下的重建精度相当，但是在Cartesian欠采样模式下的重建细节要好一些。

表3显示了四种算法在模型容量和测试时间方面的比较。可以看到DICNN的模型容量小于DCCNN，但是由于利用了切片间的数据冗余，其重建精度更高。与CRNN相比，DICNN模型容量较大，但是在重建速度上要快于CRNN。此外CRNN在迭代重建时融合了前一阶段的迭代结果，需要保存大量的中间变量，因此在实际运行时CRNN所占的显存远大于DICNN。

Fig.9 Comparison of DICNN reconstruction results under 6X different undersampling modes图9 DICNN在6倍不同欠采样模式下的重建结果比较

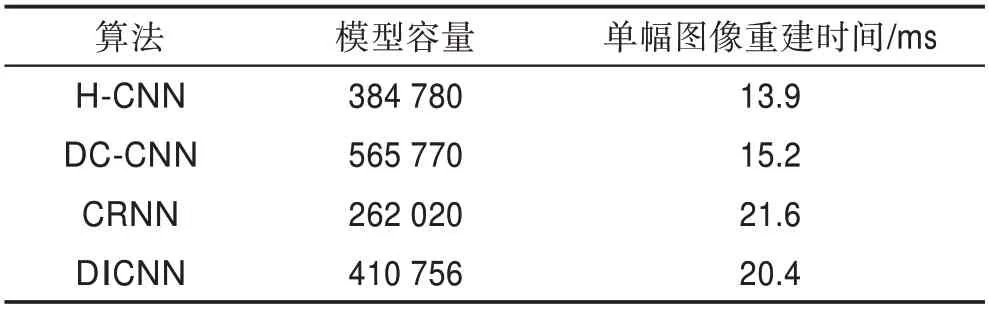
Table 3 Comparison of model capacity and reconstruction speed of four algorithms表3 四种算法在模型容量与重建速度上的比较

5 结束语

本文构建了一个用于欠采样脑部MRI重建的深度迭代卷积神经网络DICNN。为了利用脑部MRI序列中切片间与切片内的数据冗余，相应的本文构造了两个子模块BDC与RNET。其中BDC包含了双向卷积结构，可以有效地处理MRI序列数据，在训练中学习相邻切片的冗余关系。RNET包含堆叠的2D卷积层，可以进一步处理单幅切片中的数据冗余关系。实验仿真证明，DICNN能够有效利用脑部MRI切片间与切片内的冗余关系作为先验知识，复原出的图像能够提供更清晰的组织结构。此外DICNN的重建速度约每秒50张，能够满足实时重建的要求。

本文的仿真实验建立在单线圈的MRI成像场景，在未来的工作中可以结合并行成像来对脑部MRI序列进行重建，以达到更高的重建质量。