稀疏重构和紧凑性结合的图像显著性检测*

张莹莹，葛洪伟+

1.江南大学江苏省模式识别与计算智能工程实验室，江苏无锡214122

2.江南大学物联网工程学院，江苏无锡214122

1 引言

近年来，计算机视觉领域发展迅速，其中涉及大量的图像处理。若能预先检测出图像中的显著目标，将极大促进视觉领域各分支方向的研究与发展。如今，显著性检测[1-2]已广泛应用于图像分割[3]、目标跟踪[4]等领域。

显著性检测的研究大都离不开先验知识，如背景先验[5]、中心先验[6]等，这些算法将图像边界部分作为背景或将中心区域视为前景目标，并在此基础上通过对比计算确定图像各区域的显著值。近几年的显著性检测方法多是以超像素为基础展开的[7-9]。有些学者探索图像区域间的联系，将图像以超像素为节点构建成无向权重图，进而计算超像素显著性。例如：Qin等[10]利用元胞自动机的传播机制不断更新超像素的显著值。Yang等[11]提出流形排序的检测方法，分别将前景或背景视为标签，通过标签传播求得超像素的显著值。Zhou等[12]将图像表示成二层稀疏图，利用显著区域的紧凑性计算显著图。另外，也有些学者将稀疏表示用于图像显著性检测。例如：Li等[13]在多尺度下构建背景字典，并将图像块投影在背景字典上求得重构系数，利用重构误差分别得到稠密重构和稀疏重构的显著图，并采用贝叶斯融合，得到了很好的结果。Huo等[14]引入局部图正则化稀疏重构算法精确地保留区域的几何结构以减少重构的不稳定性。

上述方法对于图像构成简单的场景检测效果明显，但在显著目标较小或是前景同背景颜色相近等复杂情况下往往难以正确检测出显著物体。因此，本文提出了稀疏重构和紧凑性结合的图像显著性检测算法（image saliency detection combining sparse reconstruction and compactness，SRC）。

2 稀疏重构和紧凑性结合的显著性检测

SRC对输入图像平滑预处理后将其分割成超像素。之后一方面将各超像素投影在背景模板上进行稀疏重构，采用元胞自动机（cellular automata，CA）的更新机制对重构误差传播得到初步显著图；另一方面利用显著区域的紧凑性提取前景、背景种子，分别计算基于前景种子和背景种子的显著图并融合。最后将两阶段的显著图融合输出最终结果。SRC算法框架见图1。

2.1 图像主结构提取

Fig.1 Framework of SRC algorithm图1 SRC算法框架图

显著物体通常结构完整，环境杂乱时，一些微小的背景噪声也可能导致检测结果不连续或残缺。若能减弱背景噪声，突出图像主结构，显著性计算会更准确。Jia等[15]提出的织物瑕疵检测采用相对总变差方法（relative total variation，RTV）模糊变化缓慢的灰度区域，保留边缘之类的急速变化的区域。SRC采用RTV对输入图像做保留主结构的平滑预处理。

RTV模型的目标函数为：

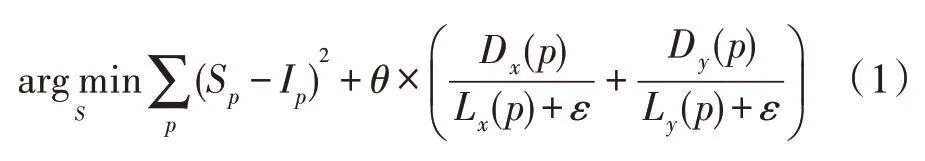
其中，p表示像素点，I是输入图像，S是输出图像，θ=0.015用来控制权重，ε是一个很小的正数，用来保证分母不为0。Dx(p)和Dy(p)分别表示像素p在x和y方向的窗口总变差，计算了窗口R(p)内的绝对空间差异，定义如下：

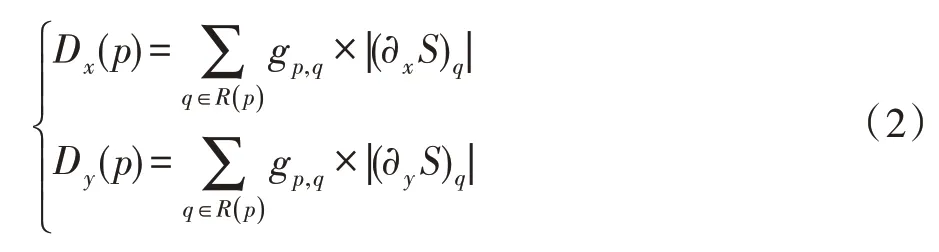
其中，R(p)是以像素p为中心的长方形区域，gp,q是由空间相关性定义的加权函数，其定义为：

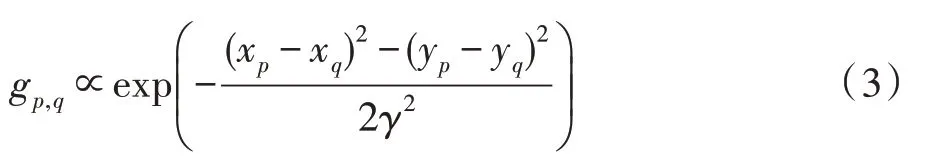
γ=3用于控制窗口的空间尺度。Lx(p)、Ly(p)为窗口固有变差，记为：

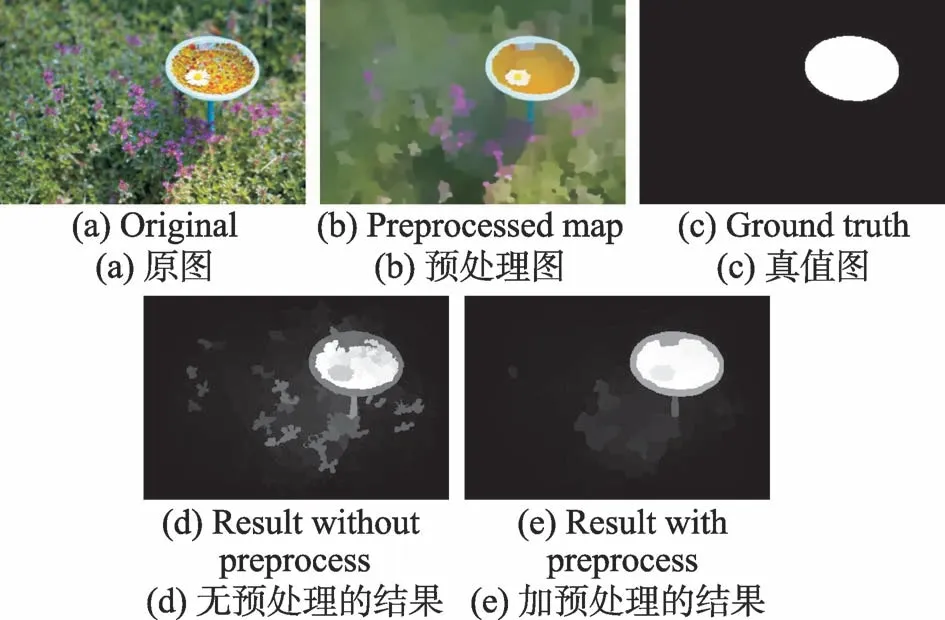
Fig.2 Effect of preprocessing图2 预处理效果

预处理可以弱化微小噪声，减轻对后续计算的干扰。由图2（b）可知，预处理后背景中的杂草变得模糊。由图2（d）和图2（e）可见，不加预处理的显著图中杂草的显著性很高，预处理后的显著图中背景的显著值则明显降低。

2.2 提取背景模板

利用简单线性迭代聚类（simple linear iterative clustering，SLIC）[16]将平滑后的图像分割成N个超像素。将每个超像素块用所含像素点的RGB和Lab两种颜色特征以及超像素位置坐标构成的8维特征向量x={L,a,b,R,G,B,x,y}T表示，整幅图像可以表示为X=[x1,x2,…,xN]∈RD×N，D表示特征维度。

通常认为，显著物体位于图像中心附近，而图像的四周则属于背景，在此基础上，多数基于稀疏重构的算法提取图像四周的超像素块作为背景模板。考虑到显著物体位于图像边缘的情况，SRC利用边界连通性[17]从图像四周的超像素块中除去属于背景的可能性较小的超像素，将剩余的超像素视为背景模板。边界连通性认为前景与图像边界的连接程度小于背景与图像边界的连接程度，据此将超像素属于背景的概率定义为：

其中，Lenbnd(i)代表第i个超像素的边界长度，Area(i)代表第i个超像素的面积。BndCon(i)越小，说明第i个超像素与图像边界的连接程度越小，它属于前景物体的概率也就越大。将位于图像四周的BndCon(i)＜0.5的超像素视为前景除去，提取剩余超像素视作背景模板，将背景模板的D维特征表示成b，由此构成背景模板集B=[b1,b2,…,bM]，M为背景模板中超像素的个数。

相比将图像四周的所有超像素视为背景，本文提取背景模板的方法更贴合实际情况，这样后续计算所有超像素在背景模板上的稀疏重构误差时得到的结果也更准确。

2.3 基于稀疏重构的显著图

稀疏重构在检测复杂场景时表现出很好的鲁棒性，具有较强的背景噪声抑制能力[13]。将背景模板B作为稀疏重构的字典，将各个超像素投影在该字典上进行稀疏重构，采用式（6）计算第i个超像素的重构系数：

其中，λ是一个用来平衡等号右边两项重要性的参数，即用来调节误差项和稀疏约束项||αi||1的重要程度。λ越大对αi的稀疏性约束越强。反之，则表示更加强调重构误差越小越好，λ在这里取0.01。利用重构系数可得第i个超像素在背景字典上的稀疏重构误差：

前景与背景通常差别较大，在同一字典上的稀疏重构误差也会有较大差异。若超像素属于背景，将它投影在背景字典上进行重构的误差就会很小，而前景在背景字典上的重构误差则比较大，因此可以利用重构误差的大小粗略区分前景背景。图3（b）是重构误差图，可以看到，前景的重构误差较大，亮度较高，而背景区域因误差很小，显得比较暗。

CA是显著性检测中常用的传播机制[10]，它可以将图像初始显著值更新到更稳定准确的状态。将超像素视为CA模型中的元胞，利用区域间的信息将重构误差视为初始显著值不断更新直至稳定，并将得到的结果分配给对应超像素包含的所有像素点便得到基于稀疏重构误差的显著图S1。图3（c）是对重构误差CA传播后的结果，它使显著区域内部更加均匀。

Fig.3 Effect of sparse reconstruction图3 稀疏重构效果

2.4 基于紧凑性的显著图

图像中背景区域往往比较松散，前景物体则相对紧凑，因此可以根据区域的紧凑性判断该区域的显著程度。首先根据RGB、Lab组成的六维颜色特征用K-means算法将N个超像素分成K类，令F=[f1,f2,…,fK]表示K个聚类中心，计算各超像素和每一类之间的相似性，可得相似性矩阵A=[aij]N×K，aij为：

其中，σ2=0.1，ci表示第i个超像素的颜色特征向量，fj表示第j类的聚类中心。

文献[10]中的流形排序算法经常用来传播超像素间的相关性，该算法以超像素为节点将图像表示成G=(V,E)的形式，V表示节点集，E是边集，eij∈E表示节点vi和vj相连，利用超像素包含像素点的Lab平均颜色特征计算边的权值。为提高准确性，SRC采用RGB、Lab两种颜色特征和稀疏重构误差计算边权值，将超像素vi和vj的相关性表示为：

若第j类属于背景，sv(j)就会比较大，将第j类属于前景的可能性定义为p(j)=1-sv(j)，采用p的平均值将这K类划分为前景种子和背景种子，并将两类种子集合分别表示为FG和BG。

通常，与背景种子相似的往往是背景，反之则为前景，即超像素的显著性大小同它与背景的相似性成反比例关系。于是超像素vi基于背景种子的显著性可定义为：

将超像素的显著值分配给其包含的所有像素点便得到基于紧凑性的显著图S2。

图4是流形排序算法改进前后得到的基于紧凑性的显著图对比。可以看到改进后的紧凑性计算过程可以更好地突出图像中的前景目标。

Fig.4 Effect of improved manifold ranking图4 流形排序改进效果

2.5 显著图融合

与仅由稀疏重构误差得到的显著图S1相比，紧凑性计算得到的显著图S2的准确率得以提高，但召回率有时会降低。将二者融合，在准确率几乎不变的情况下召回率明显高于任一方。这是由于稀疏重构和紧凑性分别适用于不同的复杂场景。例如：图5中的松鼠与背景颜色较为相近，尤其是头部，不细看难以区分，稀疏重构凭其较强的前景突出能力突出显示松鼠身体，且给松鼠头部较高的显著值，而由紧凑性得到的显著图则将松鼠头部完全视为背景，分配给身体部分的显著值也不是很高。当物体位于图像边缘附近时，如图中的标志牌，虽然稀疏重构的背景模板中已滤除了属于前景可能性较大的超像素，但仍免不了包含少部分前景区域，这样由稀疏重构得到的显著图中前景物体的显著值略低，而紧凑性对位于任何位置的显著物体都适用，可以赋予整个显著物体较高的显著值。也就是说在不同的场景下，仅由稀疏重构或紧凑性得到的显著图的召回率高低不一致，综合考虑上述两种情况，将S1、S2融合，得到的显著图在任何情况下的召回率都不低，因此在整个数据集上评测时召回率会提高。融合过程在Matlab里仅需一行代码就可以完成，用时可以忽略不计，融合公式为：

Fig.5 Map of fusion effect图5 融合效果图

3 实验结果与分析

3.1 数据集

为验证SRC的有效性，在5个公开数据集上对其进行评估，它们分别是MSRA10K[18]、ECSSD[19]、PASCALS[20]、SOD[21]、DUT-OMRON[11]。

MSRA10K包含10 000张图像，图像构成简单，胜在数量很大，其余4个数据集图像构成相对复杂。ECSSD由1 000张图像构成，图像富含纹理特征，部分图像含多个显著物体。PASCAL-S包含850张图像，多由复杂场景构成，且包含多个显著物体。SOD仅含300张图像，但每张图像往往包含多个显著物体，且位置不一。DUT-OMRON包含5 168张图像，富含自然场景，且部分图像含多个显著物体，是一个挑战性很大的数据集。

3.2 参数设置与评价指标

超像素个数N的初始值设为300，分类个数K设为36。为了取得最佳效果，对公式中的系数多次取值进行实验。实验结果表明式（9）中η在[0.4，0.6]之间具有鲁棒性，将其设为0.5。经实验对比还发现融合式（19）中的β和式（20）中的τ在0.3～0.6内取值结果变化不大，将其统一设为0.4。

本文采用PR曲线、F-measure、MAE（mean absolute error）等常用指标以及最新提出的E-measure[22]对所有对比算法进行评估。用阈值0～255对显著图分割计算P、R值，对一个数据集中所有图片同一阈值下的P、R求平均值，得到256对P、R值，绘制可得PR曲线。采用图中所有像素点显著值平均值的2倍为阈值计算指标F-measure:

其中，β2=0.3用来强调P的重要性。

MAE用来评估显著图和标准真值图之间的像素级的平均绝对误差：

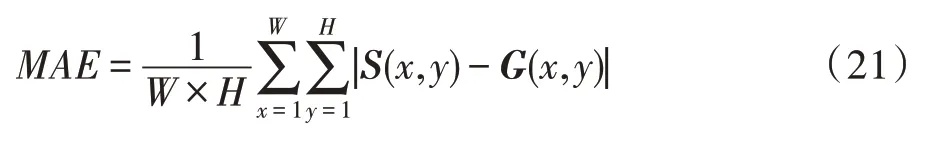
其中，S(x,y)是由算法得到的显著图，G(x,y)是标准真值图，W和H分别是图像的宽和高。

3.3 实验对比与分析

为验证所提算法的有效性，将SRC同近几年提出的13种算法从多方面进行对比，分别为：DP（salient region detection using diffusion process on a two-layer sparse graph）[12]、DSR（saliency detection via dense and sparse reconstruction）[13]、IDCL（salient region detection via integrating diffusion-based compactness and local contrast）[6]、BFS（saliency detection via background and foreground seed selection）[5]、MAP（saliency region detection based on Markov absorption probabilities）[23]、BSCA（background-based map optimized via single-layer cellular automata）[10]、LPS（inner and inter label propagation:salient object detection in the wild）[24]、MC（saliency detection via absorbing Markov chain）[8]、GBMR（saliency detection via graph-based manifold ranking）[11]、MS（saliency detection with multi-scale superpixels）[7]、WMR（saliency detection via affinity graph learning and weighted manifold ranking）[25]、RRWR（robust saliency detection via regularized random walks ranking）[26]、RCRR（reversion correction and regularized random walk ranking for saliency detection）[1]。

图6列举了几幅具有代表性的图片。其中，第2幅图像包含多个显著目标，对比算法能检测出显著目标的范围，却不能区分各个显著物体，而SRC可以较好地区分它们。第3幅图中大海和蓝天占据大部分空间，而飞机所占空间极小，在这种情况下，多数算法如BFS、LPS、MS、WMR等无法检测出飞机而将蓝天和大海视为显著的，DP、DSR等虽能检测出飞机，但不能充分抑制背景，而SRC却可以清晰地检测出飞机并充分抑制背景。多数算法对先验知识的不合理使用使误差增大，如BFS、GBMR等使用背景先验时将图像四周全视为背景，BFS使用中心先验时假定显著物体位于图像中心附近。仅利用紧凑性得到的显著图，如DP算法能检测出显著物体，但对背景噪声的抑制能力较差，仅利用稀疏重构却又可能将边缘的显著物体视为背景，将二者融合得到的显著图可适用于大部分场景，相比其他算法具有更强的前景突出和背景抑制能力。

Fig.6 Visual comparison of 14 detection methods图6 14种检测方法的视觉对比

图7是各算法在5个数据集上的PR曲线，由于MSRA10K数据集图像构成比较简单，符合显著性检测中常用的先验知识，因此各算法在该数据集上效果显著，PR曲线重叠较多不易区分，但仍能看出SRC效果略有提升，图8（a）再次验证了这一点。在其余4个复杂数据集上，SRC的PR曲线包围大部分对比算法的PR曲线，而图8中SRC的P、R、F值高于所有对比算法，也高于仅利用紧凑性计算显著性的方法DP。这是因为稀疏重构、紧凑性计算分别在不同的场景下取得较好的检测效果。稀疏重构的准确性依赖于背景模板的提取，SRC利用图像四周的超像素构建背景模板，有可能会漏掉图像中心的背景，SRC对背景模板改进时虽滤除了其中属于前景可能性较大的超像素，无法准确除去全部前景部分，当物体位于边缘部分较多中心区域全是背景时利用稀疏重构误差确定图像显著性的方法效果不佳，这时就需要紧凑性计算赋予前景物体较高的显著值。当显著物体不在边缘附近但前景与背景颜色相近时仅利用紧凑性计算难以区分前景背景的交界处，还有可能检测不出与背景极为相似的前景，而稀疏重构凭借其优秀的前景突出能力可以赋予前景较高的显著值。综上所述，稀疏重构和紧凑性相辅相成，结合所得的算法在前景突出和背景抑制方面优于所有对比算法。

表1是各算法的平均绝对误差MAE。可以看到，SRC在多个数据集上具有最小的MAE值。仅DSR算法在DUT-OMRON上的MAE略低于SRC，这是因为该数据集中的显著物体种类大小不一，DSR在8个尺度下计算显著图并融合，误差相对较小。表2的E-measure描述了显著图的结构完整性。Emeasure越大，说明显著图的结构越完整。SRC算法的E-measure值在任一个数据集上均优于所有对比算法，这说明结合稀疏重构和紧凑性获得的显著图结构更完整。表3显示了各算法在SOD数据集上平均处理一幅图像所需要的时间。BFS利用颜色、纹理进行边缘检测的过程耗时较长，运行最慢，单张图片处理时间约为7.479 s。DSR在8个尺度下计算显著图并融合，运行速度也比较慢，单张图片处理时间约为5.186 s。SRC检测一幅图像的时间约为0.841 s，速度较快但不是最优的，SRC算法中的CA模型传播显著值的过程较为耗时，对检测速度有较大影响。

Fig.7 PR curves of 14 algorithms on 5 datasets图7 14种算法在5个数据集上的PR 曲线

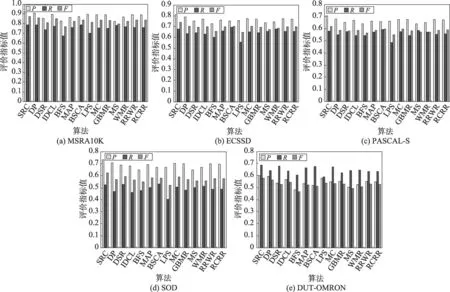
Fig.8 P、R、F values of 14 algorithms on 5 datasets图8 14种算法在5个数据集上的P、R、F 值

Table 1 Mean absolute error of all algorithms表1 所有算法的平均绝对误差

Table 2 E-measure of all algorithms表2 所有算法的E-measure

Table 3 Comparison of average running time表3 平均运行时间对比 s

4 结束语

SRC算法先对图像进行结构提取，弱化噪声，然后从稀疏重构误差和显著区域的紧凑性两方面考虑，求得两种显著图并融合得到最终结果。在5个数据集上与多种算法进行对比，无论是视觉效果还是多种评价指标都证明了SRC的有效性。在未来的学习和研究中，可以考虑形状、纹理等特征以及其他先验知识以进一步提升检测效果。