基于低秩全变差正则化的高光谱异常检测方法*

徐 超，詹天明

南京审计大学信息工程学院，南京211815

1 引言

随着成像光谱技术的快速发展，高光谱遥感在近二十年内取得了重大突破。高光谱遥感是以数百个窄频率且连续的光谱通道记录反射光成像，这些窄频率覆盖可见光、近红外和短波红外波段，光谱分辨率可达纳米数量级[1-3]。高光谱图像是三维的立方体数据，其每个像素点是一个由向量表示的光谱，每个光谱波段代表每个光谱带上反射值的辐射度[4-6]。三维的立方体则包含在这些连续波段上的一系列二维空间图像[7-8]。因此，高光谱图像较好地体现了场景的空谱联合信息。基于这一特点，高光谱图像可以更好地对地物中的不同种类进行区分以及对特定目标进行识别。因此，高光谱图像在地质学、生态学、地貌仿真、农林科技、岩石分类、大气科学、环境监测等研究领域得到了广泛的应用，为政府相关部门以及企业提供了有力的决策支持[9-10]。

图像中，有些具有特定形状的像素点与其周围环境具有较大差异的目标被称为异常目标[11]。由于高光谱图像中每个像素点包含丰富的光谱信息，与彩色图像和多光谱图像相比，高光谱图像更适用于异常检测，这在许多军事和民用应用领域中引起了人们的极大兴趣。由于异常目标往往非常小且以一种低概率形式出现，因此异常目标很难通过任何的监督手段或者肉眼观察来检测。从理论角度分析，异常检测可以看作是将图像中的像素点分为异常和背景两个类别的问题。但是在没有先验光谱信息的前提下准确检测到与周边背景有一定差异的目标是非常具有挑战性的工作[12]。

近几十年来，许多专家学者对异常检测问题进行深入分析，提出了许多异常检测方法。在高光谱异常检测研究领域，应用最为广泛的是由Reed和Yu提出的Reed-Xiaoli(RX)方法[13]。该方法假设背景服从多维高斯分布，RX算子利用多维高斯分布的概率密度函数测量待测像素属于背景的概率值。所得的广义似然比测试结果其实是输入测试像素的光谱矢量与其邻域内背景均值的马氏距离。但在实际应用场景中，由于噪声和异常像素的存在，用多维高斯分布描述复杂的背景存在较大的误差。因此许多改进算法纷纷被提出，例如基于正则化的RX算法[14]、基于分割的RX算法[15]、基于线性滤波器的RX算法[16]、核RX算法[17]等。此外，一些没有基于RX算法的异常检测方法也被广泛提出，其中基于表示学习的异常检测方法在近几年受到了广泛关注。这类方法假设高光谱特征可由字典线性表示。通过对表示系数进行约束，可以得到不同的检测算子。其中，比较知名的表示学习检测算法有稀疏表示的异常检测算法[18]、协同表示的异常检测算法[19]，以及低秩表示的异常检测算法[20]。

基于低秩表示的异常检测算法将高光谱图像分为背景和异常两个部分，并对背景部分进行低秩约束。异常区域则可通过原始图像和恢复背景区域的残差求得。但是，高光谱图像中存在大量的混合像元以及噪声的干扰，该方法会将部分属于背景的像素点错误划分为异常目标。为此，本文提出一种基于低秩和全变差（total variation，TV）正则化约束的高光谱异常检测方法。首先，针对混合像元的问题，利用线性和非线性解混方法提取高光谱图像的丰度图，将丰度图与原始图像进行融合得到待检测的图像。其次，在融合数据中构建背景区域的字典，并构建图像的低秩表示模型。然后，对背景的表示系数进行低秩约束，对表示异常的光谱维进行TV正则化约束，建立异常检测的低秩和TV正则化模型。最后，通过最优化目标函数，求解分类结果得到异常检测结果。在三组典型的高光谱图像中进行对比实验，结果表明本文方法与现有方法相比可获得更好的高光谱异常检测性能。

2 基于低秩表示的异常检测

设X∈ℝm×n×B表示高光谱图像，对空间域进行拉升并转置，其可以表示为I∈ℝB×N，其中N=m×n。在高光谱图像中，隶属于异常的像素点与隶属于背景的像素点是不同的，同时隶属于背景的像素点之间应存在较强的相关性。因此，文献[11]将矩阵I分解为背景和异常两部分：

I=DS+E（1）

其中，DS表示背景部分，D是由隶属于背景的像素点构成的字典，S是表示系数，而E则表示异常部分。

在已知I和D的前提下，求解S和E即可实现异常检测的目的。文献[11]认为背景像素点与其邻域的像素点相关性较强，应隶属于同一子空间，因此表示系数S应该服从低秩约束。而异常像素点与其他像素点有较强的差异性，因此可对E加上稀疏约束。高光谱异常检测转化为求解如下优化问题：

其中，rank(·)表示秩函数，λ是调节参数，||·||2,1表示矩阵l21范数。

式（2）中的优化问题是NP难问题，文献[11]指出该优化问题求解等价于求解如下的凸优化问题：

其中，||·||*表示矩阵核范数。当目标函数达到最优化，异常可由E的最优值的二范数求得：

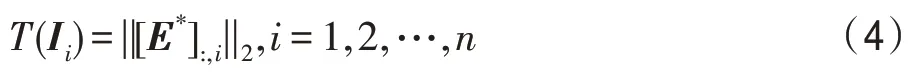
其中，E*表示E的最优值。若T(Ii)大于设定的阈值时，当前像素点Ii则隶属于异常。

3 本文方法

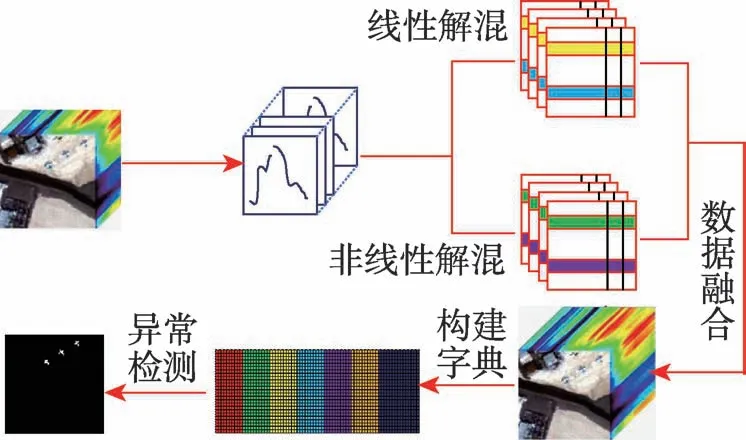
Fig.1 Flow chart of proposed method图1 本文方法流程图

为克服混合像元以及噪声对异常检测的影响，本文提出基于低秩与TV正则化的异常检测方法，图1显示了本文方法的整体流程。首先，利用光谱线性和非线性解混方法对高光谱图像进行解混，得到的丰度图像和原始图像进行融合形成待检测混合数据。其次，对挖掘背景图像特征，构建背景字典。然后，建立异常检测模型，并进行优化求解。最后，求解异常部分的二范数得到异常检测结果。

3.1 解混

高光谱图像的空间分辨率不高导致图像中存在很多由不同地物组成的混合像元，影响后续的分类和识别精度。为提升高光谱图像处理的性能，可通过光谱解混获得亚像素级的信息。目前，高光谱解混通过对每个像素的光谱进行分解，将混合像元分解为多个纯像元以及所占比例。高光谱解混主要分为线性解混和非线性解混。线性解混假设混合像元是由多个纯像元即端元的线性组合而成。而非线性解混则假设混合像元是由多个端元非线性组合而成。在已知端元的前提下，线性解混和非线性解混的目标都是求解端元对应的丰度，从而达到解混目的。目前，线性解混和非线性解混在高光谱图像应用领域各有优势，为综合利用它们这些优势，本文对高光谱图像进行线性和非线性解混，利用解混得到的丰度信息对原始高光谱图像进行信息补偿以提升后续异常检测性能。

本文利用文献[21]中的高光谱解混方法对图像进行线性和非线性解混。设Bl=[b1,b2,…,bC]∈ℝB×C表示端元矩阵，表示双线性端元矩阵，Al,An∈ℝm×n×w分别是线性和非线性解混的丰度矩阵，文献[21]中的解混目标方程为：

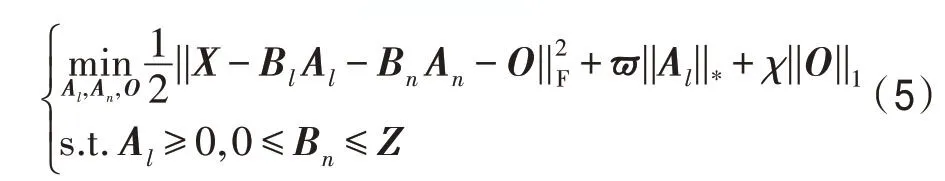
其中，ϖ和χ是非负常数，O是稀疏噪声，Z(i,j),k=

在线性和非线性解混结束后，将得到的丰度图Al,An∈ℝm×n×w叠加到原始高光谱图像X中，得到待检测的混合数据Xl=[X;Al;An]∈ℝm×n×(B+2w)。该混合数据与原始的高光谱图像相比，在光谱维上增加了亚像素级的特征，可以更好地用于不同地物的鉴别和分类中。

3.2 构建字典

字典的构建在异常检测任务中非常重要。在基于稀疏表示的目标检测方法中，由背景字典和目标字典组成的全局字典是已知的。但在异常检测中，字典是未知的，需要分析原始数据的背景和异常差异，构建完备的背景区域字典。由于异常部分在图像中所占的比例非常小，因此本文首先用文献[22]中所提的ERS（entropy rate superpixel）超像素分割方法对混合数据Xl进行分割，得到多个同质区域。ERS方法对高维数据分割速度快，且能设置生成的超像素个数，超像素边缘贴合度较好，在高光谱处理领域得到了广泛的应用。其次，将像素个数较小的超像素从数据中剔除，并将剩余的超像素按照其在图像中的顺序进行排列。然后，利用K均值算法对排列好的数据进行分类，得到K个类别。借鉴文献[11]中的预检测方法，首先将所有类别中像素个数小于一定阈值的直接剔除，然后对每个类别计算其均值μi和协方差Σi，再对每个类别中的像素计算预检测值：

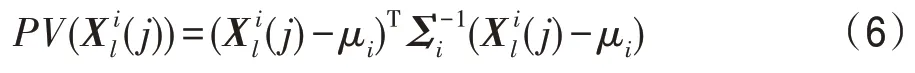
3.3 建模与优化

对Xl进行展开得到其二维矩阵的表示形式Il，与文献[11]类似，Il可由背景部分和异常部分分别表示：

其中，Sl是混合数据背景部分字典的表示系数，El是混合数据的异常部分。

为增强异常检测结果，在模型中对异常部分的光谱维引入TV正则项，结合对Sl的低秩约束，本文的变化检测模型如下：

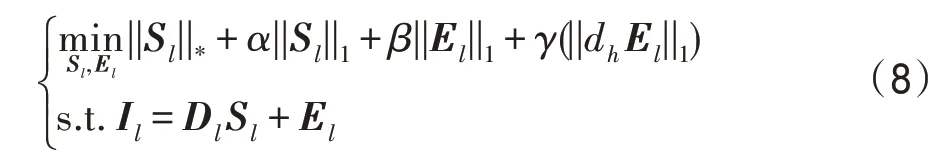
其中，模型中的第二项是对表示系数进行稀疏性约束，第四项是光谱维TV正则项，dh表示垂直方向的梯度算子。该模型结合了背景表示系数的低秩全局结构信息和稀疏局部结构信息，同时对异常部分进行了TV正则化约束，可以更好地对异常进行检测。

式（8）的最优化可用交替迭代算法[23-24]进行求解。因为式（8）对每个变量都是凸函数，因此其迭代解是收敛的。首先对目标方程进行分裂，引入中间变量J、P1和P2，满足J=Sl，P1=dhEl。原始优化问题转化为求解如下最优化问题：

3.4 算法步骤

本文提出的基于低秩与TV正则化高光谱异常检测算法总体流程如下所示：

算法1基于低秩与TV正则化高光谱异常检测算法

4 实验结果与分析

4.1 实验数据

为验证本文方法对高光谱异常检测的效果，使用三组真实高光谱图像中的包含小目标的图像块进行仿真实验。第一组高光谱图像是由机载可见光/红外成像光谱仪在美国加利福尼亚州圣地亚哥上空拍摄的。该图像空间分辨率为3.5 m/pixel，尺寸为400×400，成像波长范围从370到2 610 nm，共包含224个光谱波段，去掉38个水汽、低信噪比和信息缺失波段后，剩余186个波段用于实验[11]。图2（a）显示了该数据的伪彩色图像。第二组高光谱图像是选自HYDICE高光谱数据集。该图像空间分辨率为1 m/pixel，尺寸为307×307，光谱分辨率为10 nm，共包含227个光谱波段，去掉45个水汽和低信噪比波段后，剩余182个波段用于实验[20]。图2（b）显示了该数据的伪彩色图像。

Fig.2 Real hyperspectral image图2 真实高光谱图像

在第一组真实高光谱图像中，选择其左上角包含飞机的图像块验证本文方法。图3（a）显示了左上角图像块，其空间大小为100×100。图3（b）显示了其对应的真实异常图，包含3个共57个像素点的异常目标。在第二组真实高光谱图像中，选择右上角包含汽车和屋顶的图像块验证本文方法。图4（a）显示了右上角图像块，其空间大小为80×100。图4（b）显示了其对应的真实异常图，其中共包含9种异常目标。图5（a）显示了圣地亚哥机场中的停机坪仿真伪彩色图像。空间分辨率为100×100。在该仿真图像中植入了16个异常目标，图5（b）显示了对应的真实异常图像。

Fig.3 Image block in upper left corner of the first hyperspectral image图3 第一个高光谱图像左上角图像块

Fig.4 Image block in upper right corner of the second hyperspectral image图4 第二个高光谱图像右上角图像块

Fig.5 Simulated image block of airport in the first hyperspectral image图5 第一个高光谱图像停机坪仿真图像块

4.2 参数分析

本文方法在字典构建时主要参数包括预检测时的类别个数K，构建每个类别子字典的p值参考文献[11]分别取K=15,p=20。在预检测前进行分类并将类别中像素个数小于一定阈值的直接剔除，主要是提高字典构建以及后续异常检测的效率。该阈值根据图像大小设置，针对本文中的实验数据，阈值可设为20至50。本文实验中分别设置20、30、40和50。发现不同值对检测结果影响不大，主要原因是在分类结果中每个类别的像素个数是固定的，去除像素个数较小的那些类别即可。因此，可通过分类结果将每个类别中的像素个数进行排序，再按照排序结果动态设置阈值。

本文实验发现除K值和p值外，超像素的个数对字典构建效果也有较大影响。图6～图8分别显示了图3（a）、图4（a）和图5（a）选取100、200、300、400，300、400、500、600以及300、400、500、600个超像素的分割结果。从分割结果中看出，图3（a）选取300个超像素时异常目标的分割结果较好，图4（a）选取500个超像素时异常目标的分割结果较好，而图5（a）选取500个超像素时异常目标的分割结果较好。

Fig.6 Different scales superpixel image in Fig.3(a)图6 图3(a)不同尺度超像素图

Fig.7 Different scales superpixel image in Fig.4(a)图7 图4(a)不同尺度超像素图

Fig.8 Different scales superpixel image in Fig.5(a)图8 图5(a)不同尺度超像素图

本文异常检测模型中包含参数α、β和λ。参考文献[11]α和β值分别设为α=0.1，β=0.1。固定α和β值后，用AUC（area under curve）曲线显示不同λ值对检测结果的影响。图9显示了两组数据集中选取不同λ值的AUC值。从图中可以看出，当值λ选取过大时，检测精度有所下降，这是因为λ值较大，模型中光谱邻域信息的约束增强。而当λ值较小时，TV项的约束对检测结果起不到应有影响。因此，λ值的合理范围设定在[0.000 1,0.001 0] 。本文实验中，设λ=0.000 5。

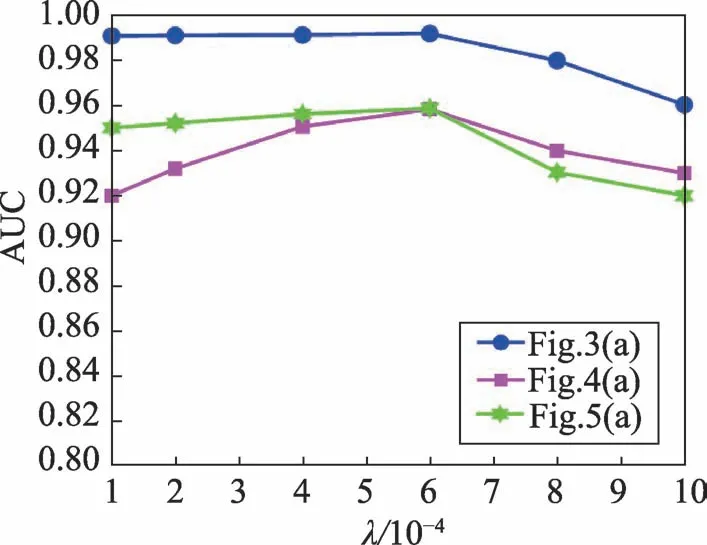
Fig.9 AUC curve obtained by different λ values图9 不同λ 值得到AUC曲线图

4.3 对比分析

为验证本文方法在高光谱图像中的异常检测效果，在两个数据集中与global-RX[13]、SRD（sparse representation-based detector）[25]、RPCA-RX（robust principal component analysis-RX）[13,26]以及LRASR（low-rank and sparse representation）[11]算法所取得的检测结果进行对比。同时为分析线性解混和非线性解混的性能，用线性解混和非线性解混分别与本文3.3节所提异常检测模型结合进行异常检测（简称LU-LRTV（linear unmixing-low rank and total variation）和NLU-LRTV（nonlinear unmixing-low rank and total variation）方法）。图10、图11和图12分别显示了不同方法在图3（a）、图4（a）和图5（a）上的异常检测结果。从图中可以看出本文所提方法由于利用了解混后的丰度图以及在检测模型中增加了低秩和TV正则化约束，其结果不仅可以较为准确地检测出异常区域，此外从结果中可以看出若只用线性解混或者非线性解混，其检测结果都没有本文所用线性-非线性融合的检测效果好。说明线性解混和非线性解混在高光谱异常检测任务中各有优势，将其融合使用则可以得到最高的检测精度。

Fig.10 Anomaly detection results of different methods in Fig.3(a)图10 不同方法对图3(a)异常检测结果图

Fig.11 Anomaly detection results of different methods in Fig.4(a)图11 不同方法对图4(a)异常检测结果图

Fig.12 Anomaly detection results of different methods in Fig.5(a)图12 不同方法对图5(a)异常检测结果图

为定量分析不同方法的检测精度，表1显示了不同算法在两组数据集上检测结果的AUC值，AUC值越高说明检测精度越好。从表中结果可知本文方法在实验所用三组高光谱图像异常检测中都取得了比其他方法更优的结果。同时，对异常目标较大的检测，本文方法的检测精度最高，AUC值可以达到0.992 0。表2列出了本文方法在三组数据集中的检测速度，在100×100×186以及80×100×172大小的高光谱图像变化检测任务中其速度分别在30 s和15 s左右，可以看出本文方法的检测速度较快，可满足实际应用需求。

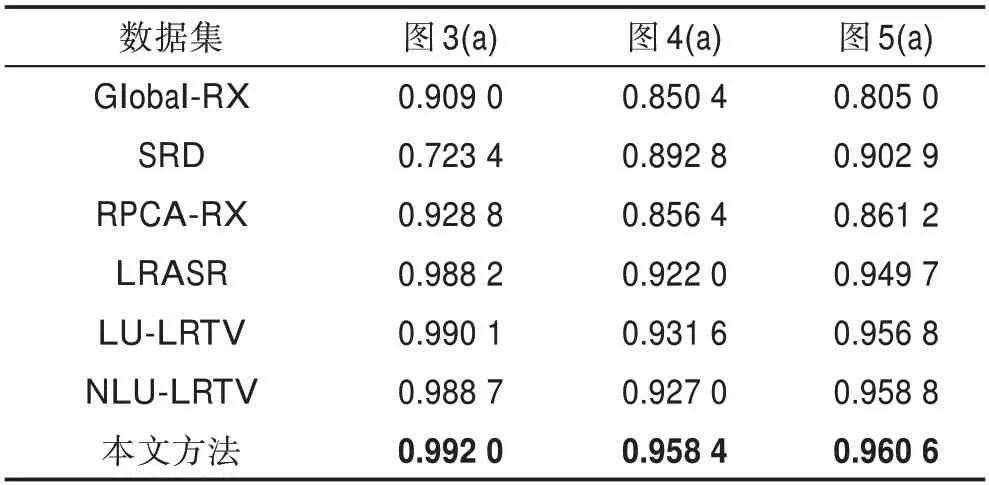
Table 1 AUC values of different methods on three datasets表1 不同方法在三组数据集上的AUC值

Table 2 Detection time of proposed method on three datasets表2 本文方法在三组数据集上的检测时间s

5 结论

针对高光谱图像异常检测问题，本文提出了一种基于低秩正则化约束的高光谱异常检测方法。该方法主要分为四个步骤：（1）端元提取后对高光谱图像进行线性和非线性解混，将得到的两组丰度图像与原高光谱图像进行融合；（2）根据背景区域在融合数据中的特征并利用超像素分割结果构建图像背景的字典，同时构建图像的低秩表示模型；（3）由背景和异常目标各自特点，建立异常检测正则化模型；（4）对模型进行优化求解，得到异常检测结果。在两组真实高光谱图像数据集中进行实验，并与经典的高光谱图像异常检测方法的检测结果进行对比分析，结果表明本文方法可获得较优的高光谱异常检测的性能。