基于加权网格和信息熵的并行密度聚类算法*

胡 健，徐锴滨，毛伊敏+

1.江西理工大学信息工程学院，江西赣州341000

2.江西理工大学应用科学学院信息工程系，江西赣州341000

1 引言

聚类算法是一种无监督的学习算法，能够根据数据对象的相关特征，将相似的对象归为一类，而差别较大的数据对象则划分到不同类中，因此聚类算法可以从样本数据中发现潜在的分布模式，被广泛应用于文本分析、生物学、医学、卫星图像分析等各种领域[1]。在聚类算法中，基于密度的聚类算法，如DBSCAN[2]（density-based spatial clustering of applications with noise）和OPTICS[3]算法，可以发现任意形状的簇且对噪声不敏感，受到人们的广泛关注[4-6]。

随着互联网信息技术的不断发展以及大数据时代的到来，使得大数据相较于传统数据，具有了4V特性[7]——Volume（数量大）、Variety（种类多）、Velocity（速度快）、Value（价值密度低）。但是传统的密度聚类算法所需的时间复杂度较高，只适用于较小规模的数据集，而在处理大数据时无疑会产生更庞大的计算复杂度[8]。因此，如何降低密度聚类算法的计算复杂度，将其应用到大数据上，是个具有挑战性的难题。

随着Google开发的MapReduce架构的广泛应用，以Hadoop、Spark为代表的分布式计算架构受到了越来越多的关注[9-10]。为了能进一步降低密度聚类算法的计算复杂度，通过改进传统的密度聚类算法，并与分布式计算架构相结合成为目前密度聚类算法研究的主要方向[11-14]。Li等人[15]首先提出了基于Map-Reduce下的并行DBSCAN算法，其使用MapReduce计算架构，将数据分片后并行执行DBSCAN算法形成局部簇，再通过增量的方式合并得到全局簇，实现了DBSCAN算法的并行化，然而该算法没有提出有效方法来划分数据，合并局部簇的计算复杂度较高。Silva等人[16]提出了MapReduce下的分布式DBSCAN算法，根据特定场景划分数据，聚类簇的合并采用增量的方式，算法的时间复杂度较高，算法总体并行化效率较低。文献[17-18]分别提出了基于Hadoop和基于Spark下的并行密度聚类算法，有效降低密度聚类算法的计算复杂度，同时分别给出了基于Hadoop和Spark下的数据划分方案，但算法对数据进行分区处理时未具体考虑数据特性，也没有给出有效的局部簇合并生成全局簇的方法。

如何有效地划分数据，合并局部簇一直是密度聚类算法并行化的重要研究内容[19]。由于数据网格化能将空间数据划分为有限数目的单元，落入同一网格的点可以被看作一个对象进行处理，可以很好地解决数据划分的问题[20]。因此，He等人[21]提出MRDBSCAN（efficient parallel density-based clustering algorithm using MapReduce）算法，采用均匀划分网格的方式将数据网格化，以网格单元作为对象并行执行DBSCAN算法，最后合并这些网格对象得到全局簇。然而算法明显存在两个问题：均匀划分网格时，网格单元的大小实际难以确定，算法的聚类效果受网格单元大小的影响较大，导致算法的聚类效果不佳；另外，算法在合并局部簇时采用增量的方式，计算效率仍然较低。在此基础上，文献[22-23]分别提出了基于Hadoop下的H-DBSCAN算法和基于Spark下的S-DBSCAN算法，同样是采用均分网格的方法来划分数据，不同的是它们通过加入网格边界的扩展，以此来提高聚类结果的精确度和局部簇的合并效率。为了能更有效地划分网格，以及进一步加快合并局部簇的效率，王兴等人[24]提出增量并行化快速聚类算法IP-DBSCAN（incremental parallelization of fast clustering based on DBSCAN algorithm）。该算法主要分为三个阶段：首先通过二分法和贪心算法对空间数据进行合理网格化；其次进行本地局部聚类，获得局部簇候选集；最后使用R*-tree索引策略进一步提高局部簇的合并速度。相较于其他按网格划分数据的并行密度聚类算法，IP-DBSCAN算法能更加合理地对数据进行划分，且在合并局部簇时加快了收敛速度，从而进一步加快了算法的并行化效率。然而该算法仍存在两个明显的不足：一方面，算法采用二分法划分数据时，仍需要输入网格边长阈值，阈值的不同会影响算法的聚类结果准确度，导致聚类结果的准确度不高；另一方面，在进行本地局部聚类时计算复杂度较高，在合并局部簇时没有采用并行化的思想，算法总体并行化效率有待进一步提升。针对上述算法存在的问题，本文主要做了以下几方面工作：（1）在数据划分阶段，根据空间中数据点的分布状况，提出ADG（adaptive division grid）策略来自适应划分网格。（2）在完成数据划分之后，为提高局部聚类效果，针对每个数据分区，提出NE（neighboring expand）策略构建其加权网格用于加强网格之间的关联性；同时提出WGIE（weighted grid and information entropy）策略来计算网格密度以及密度聚类算法的ε邻域和核心对象，使密度聚类算法更适用于加权网格；最后为解决并行密度聚类算法对局部簇的计算效率较低的问题，提出基于MapReduce的并行局部簇聚类算法COMCORE-MR（core clusters computing algorithm based on MapReduce）。（3）在局部聚类完成后，为进一步加快局部簇合并的收敛速度，提出了基于并查集的局部簇合并算法MECORE（merge core cluster）；接着结合MapReduce计算模型，提出了基于MapReduce的并行化合并局部簇算法MECORE-MR（merge core cluster by using MapReduce），实现并行化合并局部簇，从而进一步提升算法总体并行化效率，更快地获取聚类结果的全局簇，提升了并行密度聚类算法对局部簇合并效率。

2 算法及相关概念介绍

2.1 加权网格

加权网格[20]表示为WG=(G,N(G),W)，其中G=gi表示一个网格单元，N(G)=N(gi)表示与网格单元gi相关联的其余网格单元集合，W=w(gi,N(gi))表示网格单元gi与其余网格单元的权值。

2.2 均匀网格划分

均匀网格划分[25]的思想是：对于给定的数据空间，其维度为D，则将每一维的数据分成n个具有相同大小且互不相交的区间，因此D维数据空间就被划分为nd个相等的网格单元。如图1所示，若D=2，n=3，则该二维数据空间被划分为9个相等的网格单元。

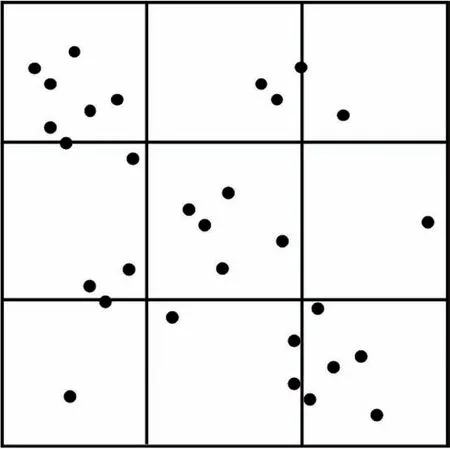
Fig.1 Uniform grid division图1 均匀网格划分

2.3 信息熵

对于一个离散型的变量X，其信息熵[26]公式为：

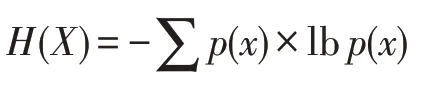
其中，p(x)为离散变量X在系统事件中出现的概率。

2.4 并查集

并查集[27]用一棵单独的树表示每一个集合，树的根节点表示该集合的代表，树的每个叶子节点表示集合中的一个元素。对于一组不相交的动态集合X={x1,x2,…,xn}和Y={y1,y2,…,yn}，利用并查集对其进行合并一般分为三个步骤：

makeset(X,Y)阶段：分别将集合X和集合Y建立一个新的并查集，其中包含n个单元素集合。

find(x)阶段：返回元素x所在集合的代表。

unionset(x,y)阶段：若元素x和元素y所在的集合不相交，则合并x和y所在的集合。

3 DBWGIE-MR算法

3.1 算法思想

DBWGIE-MR（density-based clustering algorithm by using weighted grid and information entropy based on MapReduce）算法的思想是：（1）根据数据点空间分布状况，提出ADG策略来自适应划分网格。（2）对每个数据分区，提出NE策略构建其加权网格用于加强网格之间的关联性，以此提高聚类效果；同时提出WGIE策略来计算网格密度以及密度聚类算法的ε邻域和核心对象，使密度聚类算法更适用于加权网格；最后结合MapReduce计算模型，提出并行的局部簇聚类算法COMCORE-MR，解决并行密度聚类算法对局部簇的计算效率较低的问题，从而提升算法的总体并行化效率。（3）在局部簇生成后，基于并查集的合并方法，提出了基于并查集的局部簇合并算法MECORE，用于加快合并局部簇的收敛速度；接着结合MapReduce计算模型，提出了基于MapReduce的并行化合并局部簇算法MECORE-MR，实现并行化合并局部簇，从而进一步提升算法总体并行化效率，实现了并行化地合并局部簇，从而更快地得到聚类结果的全局簇，提升了基于密度的聚类算法对局部簇合并的效率。

3.2 数据划分

目前基于网格划分数据的并行化密度聚类算法中，对于网格的划分往往是采用均匀划分的方式，即在数据的某一维度上进行等分，这种划分方式存在两个缺陷：（1）网格边长选取的不确定性，即划分数据时网格的初始边长难以确定，边长大小的选取对于聚类效果的影响较大；（2）网格数据密度不一致性，即在数据网格化时未考虑大数据环境下数据的分布特性，导致划分后的网格数据密度存在不均匀的情况。针对这些问题，本文提出了ADG策略用于将数据自适应地划分为网格。ADG策略的描述如下：

先将d维数据空间等分为2d个初始网格单元，再根据网格中数据点之间分布状况来计算网格边长的划分阈值φ。当所有网格满足非空且当前边长大于划分阈值时，则停止网格划分。网格边长划分阈值φ的取值需要根据当前最小网格中的点个数和数据点分布的紧密程度，当网格单元中的数据点个数过多或者分布过于稀疏，则需要进一步划分网格，而数据点之间的最小平均距离可以体现当前网格中整体数据分布的状况，故阈值φ的计算公式如下：

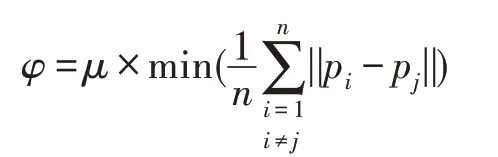
其中，pi和pj分别为d维空间中的任意两个数据点，μ为当前最小网格单元中的点个数。

ADG策略首先将整体空间划分为大小相同的数据网格，再对每一个网格做进一步细分，故其特点是将均匀网格划分与自适应网格划分相结合，从全局上数据网格的划分是非均匀的，而从局部上数据网格呈现的是均匀划分的状态。此外，由于ADG策略综合考虑了每个网格单元的数据点的数量及其分布特性，通过计算密度阈值，能对数据点较多的网格单元做进一步的细分，直到每个数据网格均满足密度阈值才会停止划分，因此最后得到的网格单元密度较为均匀，这样保证了算法计算节点的负载平衡，也为局部聚类的算法稳定性提供了保障。

3.3 局部簇形成

目前基于网格划分的并行化密度聚类算法中，局部簇的形成是通过在每个网格对象中并行执行聚类算法获得的，这种方式存在两个问题：一是在聚类过程中未能充分考虑到相邻网格之间数据的关联性，导数聚类效果不好；二是算法的计算复杂度较高，对局部簇的计算效率较低。针对这些问题，本文首先基于邻居网格和网格边界扩展原理，提出NE策略来构建每个数据分区的加权网格，加强网格之间的关联性，以此来提高聚类效果；同时，提出WGIE策略来计算网格对象的密度值，并重定义ε邻域和核心对象，使密度聚类算法更适用于加权网格；最后结合MapReduce计算模型，提出并行的局部簇聚类算法COMCORE-MR，解决并行密度聚类算法对局部簇的计算效率较低的问题，以此来提升算法的总体并行化效率。

3.3.1 加权网格构建

在对数据进行网格化处理后，为了能在聚类过程中考虑到相邻网格之间数据的关联性，进一步提升聚类效果，本文提出了NE策略来构建每个数据分区的加权网格，加强网格之间的关联性，以此来提高聚类效果。NE策略的描述如下：

首先对加权网格的作用范围进行设置。为更好地确定加权网格的作用范围，基于网格对象的邻居网格[28]，加权网格的作用范围定义如下：

NE策略通过构建每个网格对象的加权网格，使得算法在对每个网格对象进行局部聚类的过程中，不再是单一地考虑每个网格对象内部的数据关系，而是能根据每个网格对象的加权网格，综合考虑了相邻网格簇之间的连通关系以及权重关系。这样既避免了算法容易陷入局部最优，同时提高了聚类结果的精确度。

例1如图2所示，在该数据网格中有16个网格单元，数据的维度为2。

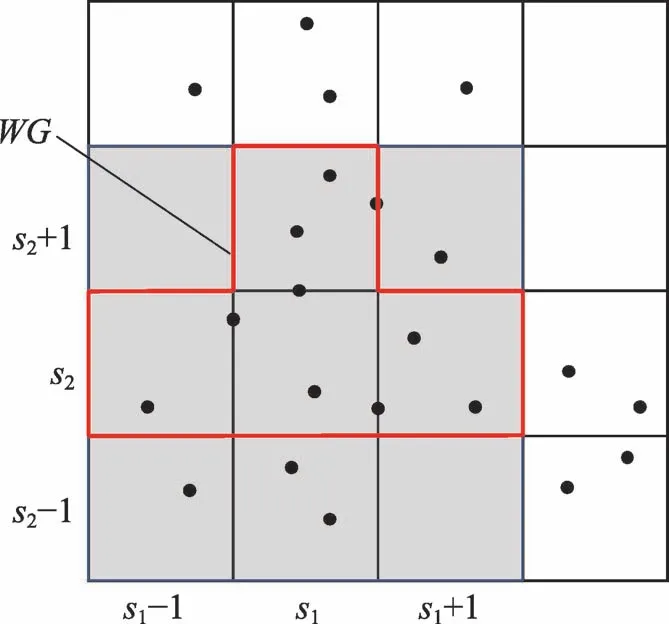
Fig.2 Construction of weighted grid图2 加权网格的构建

3.3.2 网格密度的计算

目前基于网格划分的并行化密度聚类算法中，网格密度的计算是使用网格中的数据点个数作为该网格对象的密度值，虽然这种密度表示方法在大多数基于密度的聚类问题中取得了较好效果，但在基于加权网格的密度聚类问题中，由于不同网格对象之间存在着关联性，因此直接使用网格中的数据点个数来计算加权网格中的网格密度，有失合理性。在构建好网格对象的加权网格之后，为使密度聚类算法能更好地应用于加权网格，本文提出WGIE（加权网格信息熵）策略用于计算网格单元的密度，并重新定义密度聚类算法的ε邻域和核心对象。WGIE策略定义如下：

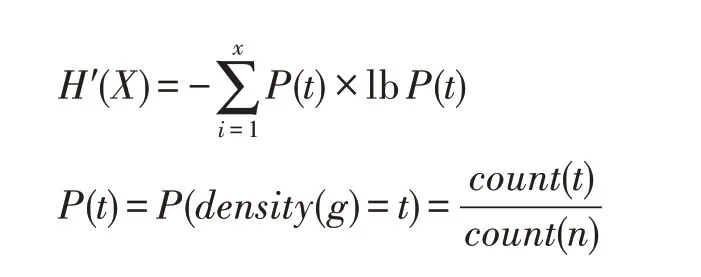
其中，t表示数据网格化后的某一非空网格单元的密度，即以该网格单元为中心构成的加权网格中的所有数据点个数；x表示该密度取值下的网格单元数量；P(t)是网格单元密度为t所出现的概率；count(t)表示网格单元中网格密度为t的网格单元个数；count(n)表示划分后的非空网格单元总数。

证明（1）单调性：对于∀t1,t2且t1-t2＞0，P(t1)-P(t2)＞0，则H′(P(t1))-H′(P(t2))＜0。

（2）非负性：因为0 ＜P(t)，lbP(t)＜0，所以0 ＜，即H′(X)＞0。

（3）累加性：对于∀t1,t2∈t，H′(P(t))=H′(P(t1,t2))=H′(P(t1)×P(t2))=H′(P(t1))+H′(P(t2))。

因此公式满足信息熵定义的基本条件，是系统稳定程度的度量公式。□

为使密度聚类算法更好地应用于加权网格，根据加权网格的作用范围和加权网格信息熵策略来重定义ε邻域和核心对象。核心对象与网格单元的密度值密切相关，采用加权网格与信息熵策略能有效刻画加权网格中网格对象的密度值，当网格单元的密度H′(X)小于给定的密度阈值μ时，则说明以该网格单元为中心的加权网格中的数据是比较有序的，因此执行聚类算法的过程中以该网格单元作为中心效果会更好，该网格单元中成为核心对象的概率越大。ε邻域和核心对象定义如下：

定义1（加权网格的ε邻域）对于一个网格对象gi，以该网格对象为中心构建加权网格后，加权网格范围内的所有网格对象为网格对象gi的ε邻域。

定义2（加权网格的核心对象）对于一个网格对象gi，若其密度满足H′(X)≤μ（即加权网格信息熵小于给定的阈值），则该网格对象为核心网格对象。包含在核心网格内的任一点均为核心对象。

3.3.3 局部聚类

在提出了网格对象的密度计算方法之后，为了能更快地进行局部聚类，进一步加快算法的总体并行化效率，本文提出基于MapReduce的并行化计算局部簇的COMCORE-MR算法。该算法主要分为两个阶段，并行计算网格密度阶段和并行计算局部簇阶段。

先在并行计算网格密度阶段，需要输入网格对象g以及网格中的点pi；接着，执行map函数计算出以网格对象g为中心的加权网格中点的数量Ci[g]，并输出Key-value值＜g,Ci[g]＞。之后，执行reduce函数合并map函数的结果，并使用WGIE策略计算出每个网格对象的网格密度hi，最后输出Key-value值＜(g,N(gi)),hi＞传入下一个阶段。如图3（a）所示。

接着在并行计算局部簇阶段，需要输入数据集D中的点pi以及上个阶段计算出的Key-value值＜(g,N(gi)),hi＞；之后，调用map函数对数据进行计算，如果输入的数据为数据点pi，则map函数计算每个数据点所对应的网格对象g并输出Key-value值＜g,pi＞，如果输入的数据为Key-value值＜(g,N(gi)),hi＞，则map函数根据定义2计算当前网格对象g是否为核心网格，如果hi≤μ，则当前网格对象g为核心网格，输出Key-value值＜g,N(gi)＞，如果hi＞μ，则不输出任何结果；最后执行reduce函数，合并map函数的结果，输出Key-value值＜(g,N(gi)),N(pi)＞。最终得到的结果便是核心簇的序列集合，即聚类结果的局部簇。如图3（b）所示。

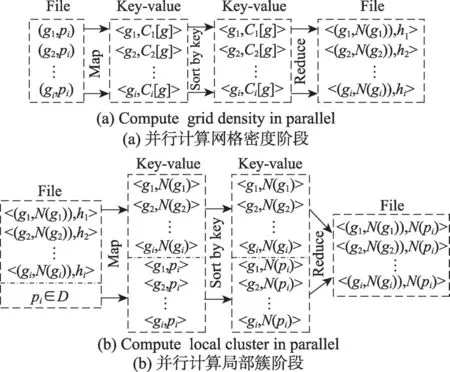
Fig.3 Process of COMCORE-MR algorithm图3 COMCORE-MR算法的计算过程

3.4 局部簇的合并

目前基于网格划分的密度聚类算法中，对局部簇的合并通常是采取增量的方式，并且没采取并行化思想，导致算法在合并局部簇时计算复杂度较高，算法总体并行化效率较低。针对这些问题，本文首先提出了基于并查集的局部簇合并算法（MECORE），用于加快合并局部簇的收敛速度；接着结合MapReduce计算模型，提出了基于MapReduce的并行化合并局部簇算法（MECORE-MR），实现并行化合并局部簇，从而进一步提升算法总体并行化效率。

3.4.1 局部簇的合并

为进一步加快合并局部簇的收敛速度，本文提出了基于并查集的合并局部簇算法（MECORE），该算法首先基于并查集对两个不相交集的合并方法，提出了基于并查集的合并不同网格对象的3个方法：Makeset、Find、Unionset。Makeset方法先将每个不同的网格对象单独处理为一个树叶节点；Find方法将处于同一局部簇中的网格对象节点相连接，返回一棵以根节点为代表的树，簇的核心网格对象作为根节点，而局部簇中的其他网格对象作为叶节点，所有的叶节点都与根节点连接；Unionset方法是将两个不同的局部簇进行合并，寻找共同的叶子节点，将其中一棵树的根节点转换为另一棵树的叶子节点。接着使用这3个方法对局部簇进行合并。算法的总体步骤如下：

对于所有的局部簇对象，将这些局部簇对象所构成的表R作为合并局部簇算法的输入，表的每一项都是核心网格对象g以及核心网格的邻域N(g)。首先，算法初始化每一个非空网格对象g∈G，将其看作一个单独的簇，每一个网格对象的状态都被初始化为unvisited，并且在算法执行之后每个网格对象的状态将变为unvisited、non-core和core这3个状态之一。接着，在输入局部簇所构成的表后，算法检索每一个核心网格对象g的Key-value值＜g,N(gi)＞，将其状态由unvisited更改为core，之后要对其邻域内的网格对象N(g)的状态进行设置，分为以下几种情况：

如果在N(g) 中的一个网格对象gi的状态为non-core，则表示当前的网格对象gi已经分配到了另一个簇中，因此网格对象gi的状态保持不变。

如果在N(g)中的一个网格对象gi的状态为core，则将以gi为核心的局部簇合并到g的局部簇中。

如果在N(g) 中的一个网格对象gi的状态为unvisited，则将其加入到以g为核心的局部簇中，并将gi的状态变更为non-core。

最后，在算法执行完之后，根据数据点和网格ID的相对应，便能得到聚类的全局簇，而被标记为unvisited的网格对象中的数据点便是离群点(outlier)。

算法具体实现如下：

3.4.2 局部簇的并行化合并

基于并查集的局部簇合并算法可以很好地对局部簇进行合并得到聚类的全局簇。为了进一步提高合并局部簇的效率，解决基于密度的并行化聚类算法中没有并行化合并局部簇的问题，本文提出了基于MapReduce的并行化合并局部簇的MECORE-MR算法。MECORE-MR算法的步骤如下：

算法需要将网格对象集G、数据集D以及表R作为输入，其中表R中的数据是COMCORE-MR算法计算出的局部簇数据。该算法首先随机地将网格对象集合G划分为数量相近的k个部分G1,G2,…,Gk，同时将表R也划分为k个部分R1,R2,…,Rk，其中k的值对应了执行算法所需要的并行节点数；接着，执行map函数，如果map函数输入的数据为数据点pi∈D，则map函数计算每个数据点所对应的网格对象g并输出Key-value值＜g,pi＞；如果输入的数据为表R中的局部簇数据，则检索该局部簇的核心网格对象的Key-value值＜g,N(gi)＞,根据Key值g在G1,G2,…,Gk中进行索引，得到相应的k值，将此核心网格对象的Key-value值分配到相应的Rk中，并输出Key-value值＜Mi,(g,N(gi))＞传递到reduce函数中去；最后执行reduce函数，对于每个Mi，并行化执行MECORE算法，将得到的k个合并结果最后执行一次局部簇合并算法，再与＜g,pi＞进行结合得到聚类全局簇。

在MECORE-MR算法中，通过并查集结构对局部簇进行合并的时间复杂度为O(i×n)，其中n为数据点个数，i为核心网格对象中点的极大值，因此其时间复杂度趋近于常量。考虑到大数据环境下，n的值较大，通过结合MapReduce可以进一步降低其时间复杂度，有效提升对局部簇的合并效率。

算法具体实现如下：

3.5 DBWGIE-MR算法的步骤

DBWGIE-MR算法具体实现步骤如下所示：

4 实验结果以及分析

4.1 实验环境

为验证DBWGIE-MR算法的性能，本文设计了相关实验。实验的硬件设备为Master主机1台和Slaver机3台，共4个节点。每一台硬件设备的处理器均为Intel®CoreTMi5-9400H CPU@2.9 GHz，内存16 GB。实验的软件编程环境均为python3.5.2；操作系统均为Ubuntu 16.04；MapReduce架构均为Apache Hadoop3.2版本。

4.2 数据来源

DBWGIE-MR算法实验数据为4个人工合成的类簇，分别是Flame、Compound、Aggregation和D31。Flame[29]是一个包含凸数据集和凹数据集的密度簇，包含240个样本点，如图4（a）所示；Compound[30]是一个拥有6个不同形状的复杂结构密度簇，共有399个样本点，这些簇之间存在着相连、内嵌、包含和不同密度重叠的情况，如图4（b）所示；Aggregation[31]拥有7个不同形状的非高斯分布的密度簇，共有788个样本点，如图4（c）所示；D31[32]则拥有31个高斯密度簇，如图4（d）所示。

4.3 评价指标

为验证DBWGIE-MR算法对数据集的聚类精确度，采用F-measure对聚类算法的结果进行评价，Fmeasure是正确率(precision)和召回率(recall)的加权平均值，计算方法如下：

通常情况下，参数λ设置为1，F-measure综合考虑了聚类结果的正确率（precision）和召回率（recall）的情况，能够较为准确地评价聚类算法的结果，当Fmeasure的值较高时，说明聚类结果更为准确合理。

4.4 参数选取

DBWGIE-MR算法通过使用ADG策略，自适应划分数据空间，并且使用NE策略和WGIE策略来计算网格对象的密度值，但对于密度阈值μ来说，仍需要指定具体的值。为了使DBWGIE-MR算法能获得更加准确的聚类结果，需要对密度阈值μ的取值进行合理的设置，本文在基于Flame数据集下，保证其他参数不变，将密度阈值μ的取值设置为[1,12]，独立运行10次，取10次的F-measure均值进行分析。从图5中可以看出，密度阈值μ的值给定得太小或者太大都会影响聚类结果的准确度。实验结果表明，在μ的值取5的时候，能得到较为准确的聚类结果。

4.5 NE策略和WGIE策略的有效性分析

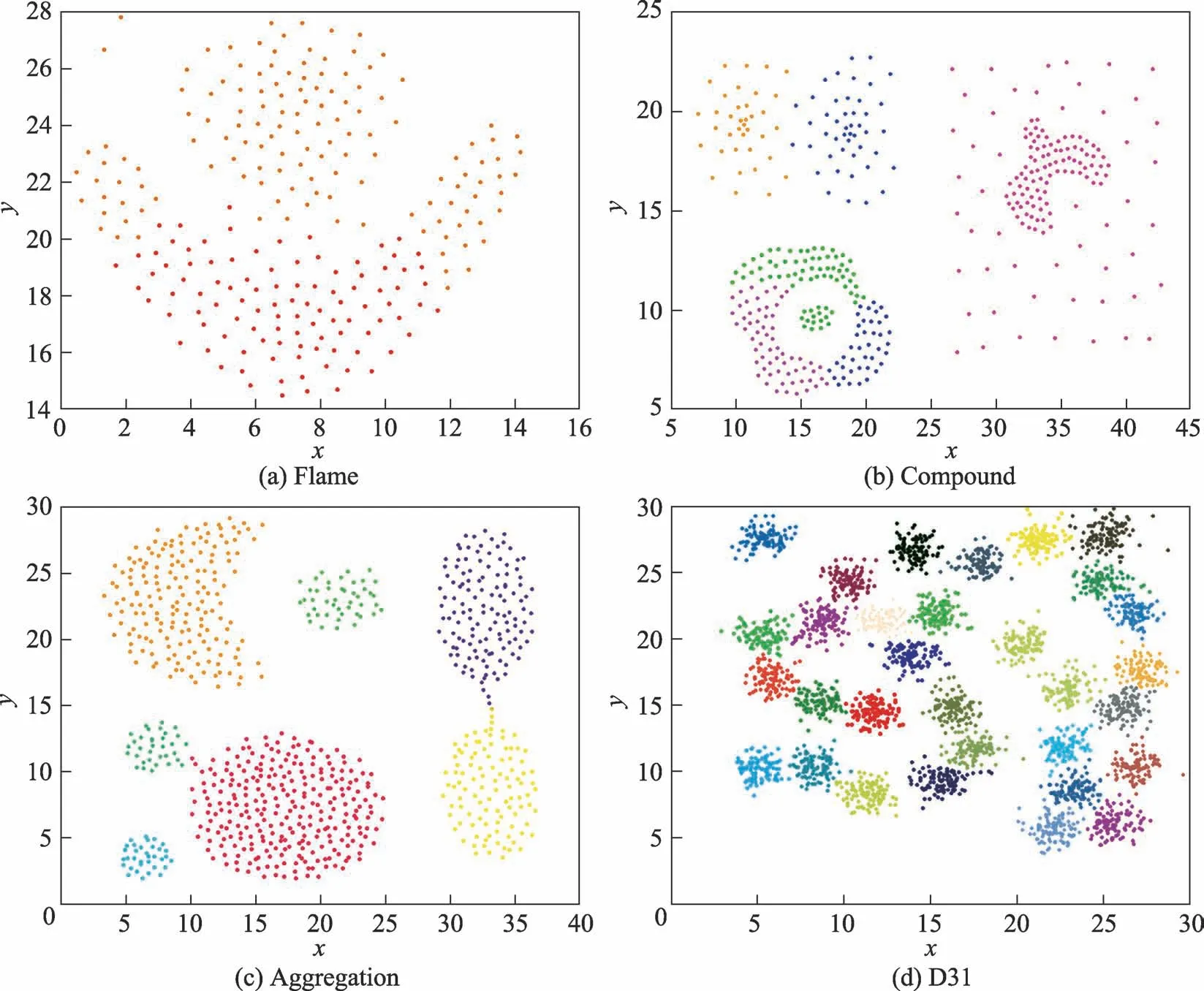
Fig.4 Dataset of experiment图4 实验数据集

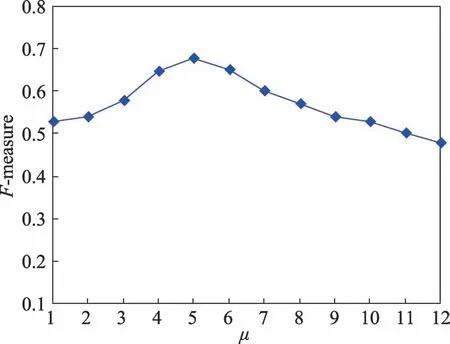
Fig.5 Selection of density value图5 密度阈值的选取

为验证NE策略和WGIE策略进行局部聚类的有效性，实验中利用本文算法DBWGIE-MR，分别采用不同的局部聚类方式，比较在不同聚类数目下的Fmeasure值的变化。将MR-DBSCAN[21]、H-DBSCAN[22]算法中的局部聚类方法与本文的基于NE策略和WGIE策略的局部聚类方式进行对比实验，图6为运行次数在[0,10]范围内变化时，分别采用3种不同的局部聚类方式的聚类效果。

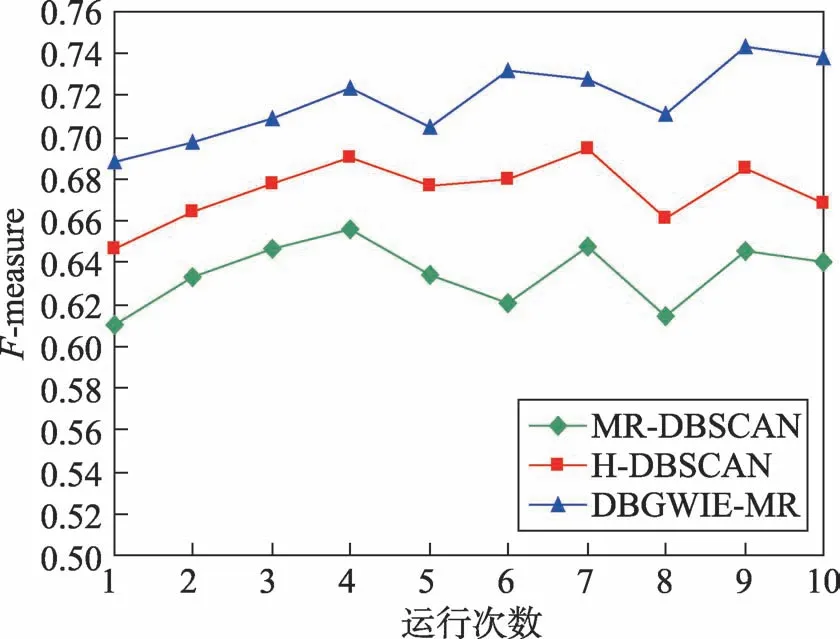
Fig.6 Comparison of results in different local cluster algorithms图6 不同局部聚类方式下的聚类效果比较

从图6中可以看出，本文通过NE策略和WGIE策略，以加权网格的方式进行局部聚类的效果明显优于采用MR-DBSCAN和H-DBSCAN算法的局部聚类方式。当采用这3种不同的局部聚类方式的聚类效果相差最大时，DBWGIE-MR算法使用基于NE策略和WGIE策略的方式进行聚类时，F-measure要比采用MR-DBSCAN和H-DBSCAN算法的局部聚类方式分别高出17.8%和8.3%。由于MR-DBSCAN的局部聚类过程是在单一的网格单元中进行，使得聚类过程仅考虑到网格对象内部的数据关系，而孤立了不同网格中的数据关系，这种局部聚类方式考虑得不够全面，比较单一，容易使算法陷入局部最优，因此其F-measure值相对较低。H-DBSCAN算法的局部聚类方式是建立在MR-DBSCAN基础上，在单一的网格单元中进行局部聚类之后，再根据网格之间的共同边界点，对网格边界进行二次扩展，考虑了相邻网格簇之间的连通关系，因此其F-measure值优于MR-DBSCAN。但是这种改进方式是在每个网格单元完成局部聚类之后再进行重聚类，其聚类效果有待进一步提升。而DBWGIE-MR算法采用NE策略和WGIE策略，构建了每个网格对象的加权网格，并以加权网格的聚类方式，在局部聚类的整个过程中综合考虑了相邻网格簇之间的连通关系以及权重关系，对网格簇之间的关系分析得较为全面，因此采用NE策略和WGIE策略进行聚类的效果较好。

4.6 聚类结果的比较分析

为验证DBWGIE-MR算法聚类结果的精准度，本文在基于Flame、Compound、Aggregation和D31的数据集下进行实验，根据聚类结果的最优值、精确度、方差和运行时间，分别与MR-DBSCAN[21]算法和H-DBSCAN[22]算法的性能进行综合比较。聚类结果的最优值能够反映算法寻优能力的强弱程度，值越小表示寻找局部簇的能力越强；精确度可直观地反映算法聚类结果的好坏程度；运行算法20次得到聚类结果的方差能够表示算法的稳定程度，值越小表示算法越稳定；运行时间表示得到聚类结果所花费的时间。实验结果如表1所示。

从表1中可以看出，MR-DBSCAN算法的聚类效果较差，而H-DBSCAN算法的聚类效果比MRDBSCAN算法的聚类效果更好，尤其是在Flame数据集上精确度提升了0.046。因为其在数据网格化的基础上加入了对网格边界点的处理，在一定程度上克服了MR-DBSCAN算法没有考虑网格之间关联性的缺陷，具有一定的寻优能力。但由于采用的是均分网格的数据网格化方法，没有考虑到数据点的分布状况，因此H-DBSCAN算法的稳定性均不佳。而DBWGIE-MR算法在稳定性的表现上比MR-DBSCAN和H-DBSCAN算法更佳，说明DBWGIE-MR克服了以上算法的缺陷，采用ADG策略自适应地将数据划分为密度较为均匀的网格单元，保证了数据网格化的合理性，对算法计算节点的负载平衡起到一定的帮助，算法聚类过程的波动性较低，因此算法稳定性更好，DBWGIE-MR算法的方差较低；与此同时，通过采用NE策略以及WGIE策略构建加权网格以及形成加权网格的局部聚类方式，使得局部聚类的过程中能综合考虑到不同网格对象之间的关联度，避免了算法陷入局部最优，使得DBWGIE-MR算法具有较强的寻优能力，因此DBWGIE-MR算法的最优值最小；此外，DBWGIE-MR算法的运行时间比起MRDBSCAN和H-DBSCAN算法，在Flame数据集上分别降低了0.47 s和0.89 s，原因是DBWGIE-MR算法采用了并行化合并局部簇算法MECORE-MR算法，加快了合并局部簇的收敛速度，因此DBWGIE-MR算法对聚类过程的执行速度得到提升。

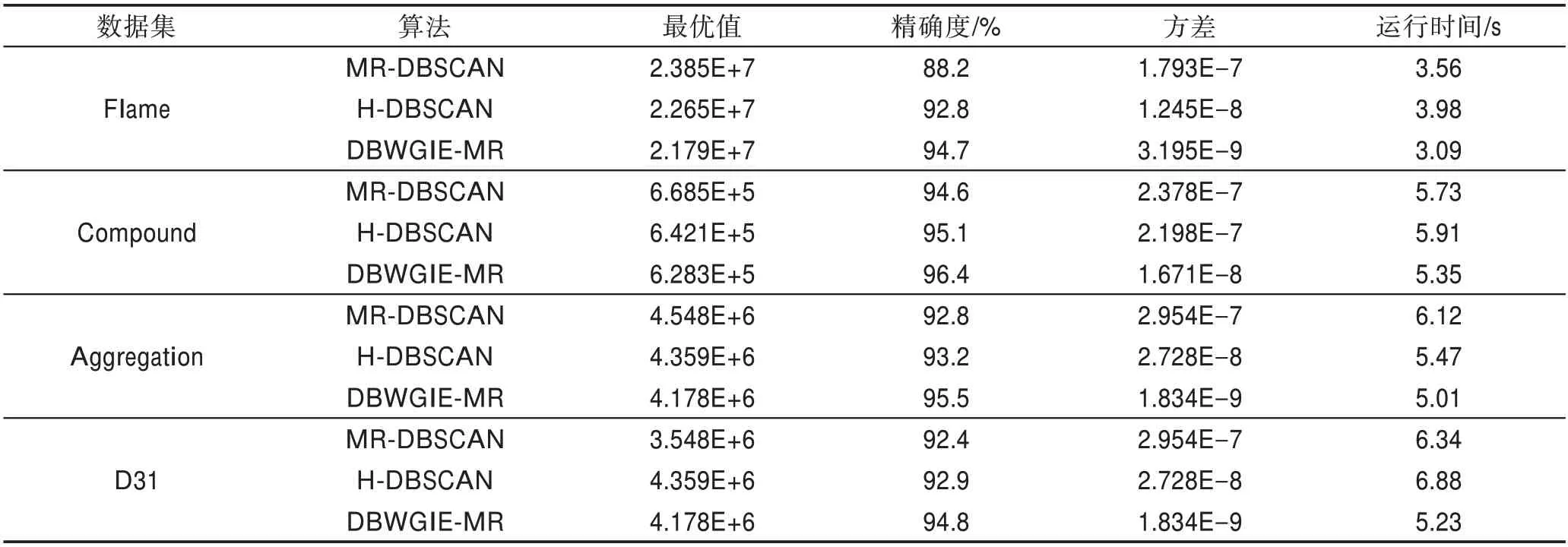
Table 1 Comparison of results in different clustering algorithms表1 各算法的聚类结果比较分析

4.7 算法性能的比较分析

为验证DBWGIE-MR算法在大数据环境下的运行性能，实验数据在基于D31数据集下进行实验，首先将D31数据集中的点数量进行扩充，构造成行数为300万行（0.6 GB）、500万行（1 GB）、1 100万行（2 GB）、1 600万行（3 GB）的大数据集。同时，为验证算法在Hadoop并行化框架下的计算能力，采用算法的加速比进行衡量。算法的加速比是指通过并行化计算使得算法的运行时间降低从而得到的性能提升，加速比通常被作为检验并行化算法性能的重要指标。在不同数据集规模下，DBWGIE-MR算法的实验结果如图7所示。

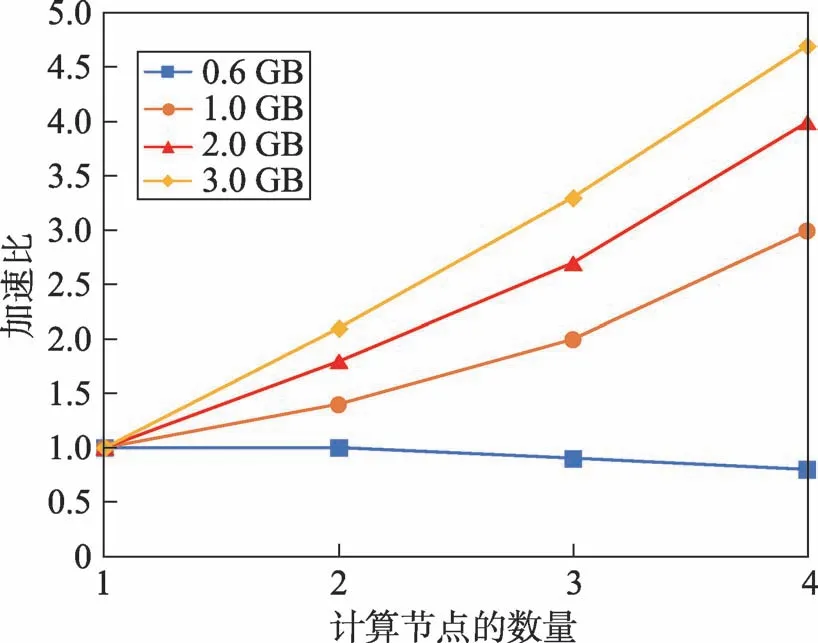
Fig.7 Acceleration rate of algorithm on different computing nodes图7 算法在不同计算节点下的加速比

从图7中可以看出，DBWGIE-MR算法在处理大数据集上具有很好的加速比。在一开始数据集较小时，如图中的0.6 GB数据量所示，随着计算节点数量的增加，加速比趋近于1.0，甚至在节点4时，出现了下降的趋势，加速比降低了0.2，这是由于在数据集的规模较小时，数据量远小于集群所处理的数据量，将数据分散到不同的计算节点中产生了不同的时间开销，包括集群运行时间、任务调度时间、节点存储时间等，这些开销降低了算法的计算速度，因此在这种情况下的并行效果是较低的；而在数据规模达到3.0 GB时，算法在4个节点下计算的加速比为4.6，比在1个节点下计算提高了3.6，原因是随着数据集规模的逐步增加，算法的能够并行化计算局部簇和合并局部簇的优点逐渐被放大，使得算法在计算节点增加的同时，加速比呈线性的增长，算法的并行化效果得到很大的提升。这也表明DBWGIE-MR算法适用于处理较大规模的数据集，并且随着计算节点的增长，并行化的效果更佳。

为进一步验证DBWGIE-MR算法在大数据下的并行化性能，将DBWGIE-MR算法的运行时间分别与MR-DBSCAN[21]、IP-DBSCAN[24]算法进行比较，所有的算法都是基于扩充后的D31数据集以及相同的并行计算节点。实验结果如图8所示。

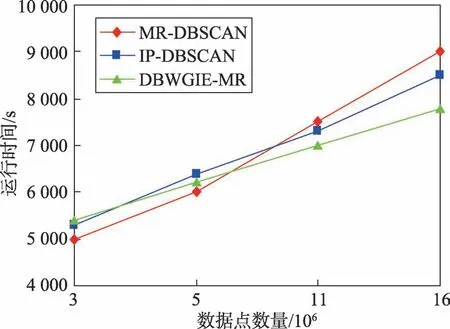
Fig.8 Running time of algorithm in different data sets图8 算法在不同数据集规模下的运行时间

从图8中可以看出，在数据集规模较小时，即数据点的数量在3×106左右时，MR-DBSCAN算法完成聚类所需的时间最少，运行时间比IP-DBSCAN算法和DBWGIE-MR算法分别减少102 s和95 s，DBWGIEMR算法执行时间则相对较长，原因是在数据集规模较小的阶段，DBWGIE-MR算法需要采用ADG策略和WGIE策略自适应地划分数据空间以及计算每个网格单元的密度，增加了算法处理数据集的时间。然而，随着数据集的规模提升，数据集的规模为11×106时，可以明显看到，IP-DBSCAN算法和DBWGIEMR算法的运行时间分别比MR-DBSCAN算法减少了160 s和400 s，原因在于在大规模数据集下，聚类过程中产生的局部簇的数量明显增加，而相较于MR-DBSCAN算法，IP-DBSCAN算法采用了并查集对局部簇进行合并，加快了局部簇的收敛，因此在合并局部簇上所需的计算时间有所减少，DBWGIE-MR算法更是在并查集合并局部簇的基础上，提出并行化合并局部簇，更进一步加快了对局部簇的合并计算，因此DBWGIE-MR算法的运行时间要少于IPDBSCAN算法；当数据规模为16×106时，DBWGIEMR算法的运行时间明显要少于MR-DBSCAN和IPDBSCAN算法，分别降低了400 s和700 s，这也更加表明了在数据规模较大的情况下，DBWGIE-MR算法能更快地对数据进行处理得到结果，并行化效果更佳。

5 结束语

为解决大数据下基于密度的聚类算法中的数据网格化划分不合理，提高聚类结果的精确度以及在大规模数据集下的并行化效率，本文提出了基于MapReduce和加权网格信息熵策略的DBWGIE-MR算法。该算法首先根据数据点空间分布状况，提出ADG策略，自适应划分网格单元；其次为了提高聚类效果，针对每个数据分区，提出NE策略构建其加权网格用于加强网格之间的关联性；同时提出WGIE策略来计算网格密度以及密度聚类算法的ε邻域和核心对象，使密度聚类算法更适用于加权网格；接着结合MapReduce计算模型，提出并行计算局部簇算法COMCORE-MR，从而提升算法的总体并行化效率；最后提出了基于并查集的局部簇合并算法MECORE，用于加快合并局部簇的收敛速度，并结合MapReduce计算模型，提出了并行合并局部簇算法MECORE-MR，实现了并行化地合并局部簇，从而更快地得到聚类结果的全局簇，提升了基于密度的聚类算法对局部簇合并的效率。与其他并行化密度聚类算法相比，该算法能根据数据之间的分布状况来自适应确定网格划分边长，以及构建加权网格来加强网格单元之间的联系，利用该算法的独特优势来实现聚类。实验在四个标准数据集上进行对比分析，结果表明DBWGIE-MR算法在聚类精度、寻优能力和算法稳定性上都有显著的提高。此外，在扩充后的大规模数据集的实验中，也验证了DBWGIE-MR算法具有较好的并行化效果。结果也表明，相比MR-DBSCAN算法和IP-DBSCAN算法，DBWGIE-MR算法在面对大规模的数据集下的并行化效率更强。虽然改进后算法的聚类精度有所提升，但仍存在提升空间，并且本文并未解决网格单元密度阈值的设置问题，算法并行化性能还有待进一步提高，以上这些将是下一步的研究工作。