浅析整体法和隔离法的选取策略

◇ 甘肃 李 栋

(作者单位:甘肃省张掖市临泽县第一中学)

受力分析是解决物理问题的关键步骤,而研究对象的选取又是受力分析的必要环节.在确定研究对象时通常会用到整体法和隔离法,尤其是在处理连接体问题时,往往随着研究对象的转化,二者要灵活交替使用.但学生在解决实际问题时,不注重研究对象的选取,受力分析往往具有随意性,很多时候将简单问题复杂化.本文将结合例题给出整体法和隔离法选取的一些策略.

例1如图1所示,倾角为θ 的斜面体C 置于水平面上,B 置于斜面上,通过细绳跨过光滑的定滑轮与A 相连接,连接B 的一段细绳与斜面平行,当A 匀速下落时,则( ).

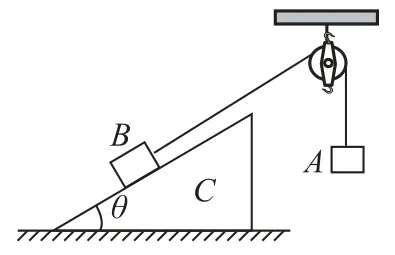
图1

A.B 受到C 的摩擦力一定不为零

B.C 受到水平面的摩擦力一定为零

C.不论B、C 间摩擦力大小、方向如何,水平面对C 的摩擦力方向一定向左

D.水平面对C 的支持力与B、C 总重力大小相等

由题意可知若A 匀速下落,则B 匀速上升,同时C 静止,所以三者的加速度均为零,因此我们在处理B、C、D 三个选项时,可以把B 和C 作为整体受力分析.如图2-甲所示,整体必受重力、地面支持力、绳的拉力作用,但这3个力的合力不可能为零,所以地面一定给B、C 整体一个向左的静摩擦力.这样很容易得出选项B、D 错误,选项C正确.

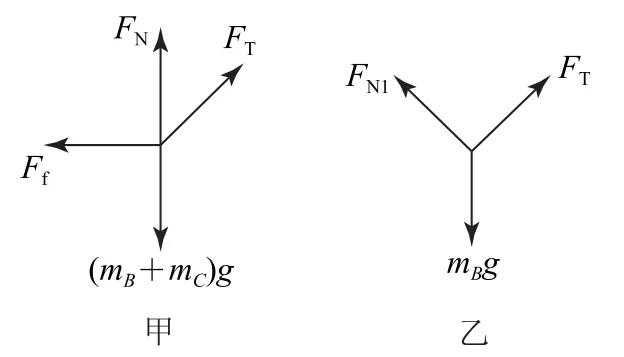
图2

再隔离B 进行受力分析,如图2-乙所示.B 必定受重力、斜面支持力和绳的拉力作用,这三个力合力可能为零,所以B 与C 间既可能存在沿斜面向上的摩擦力,也可能存在沿斜面向下的摩擦力,还可能不存在摩擦力.因此选项A 错误.

【点悟】当系统内物体具有相同加速度时(包括均处于平衡状态的物体),应优先考虑整体法,把具有相同加速度的物体作为研究对象进行受力分析,这样既可减少受力分析的个数,又能避免中间环节的烦琐推导,大大简化运算,提高解题速度;若题目中涉及物体间相互作用力(内力),则需隔离物体作为研究对象,隔离物体时,要优先隔离处于平衡状态和受力较少的物体,再进行受力分析.

例2如图3 所示,质量为m的物体A 被平行于斜面的细线拴在质量为M 的斜面上端,整个装置保持静止状态,斜面被固定在台秤上,物体与斜面间无摩擦,装置稳定后,当细线被烧断物体下滑时与静止时比较,台秤的示数( ).(重力加速度为g,物体下滑时斜面静止)

图3

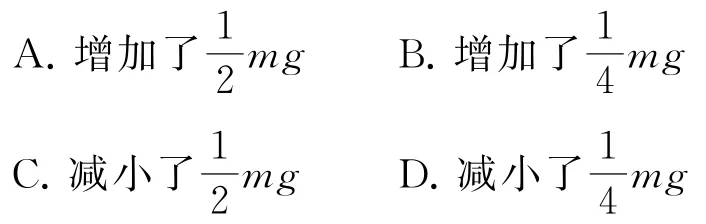
当整个装置保持静止状态时,可将物体A 和斜面作为整体受力分析如图4-甲所示,根据平衡条件和牛顿第三定律可知,整体对台秤的压力FN＝(M ＋m)g.

当烧断细绳时,隔离物体A 进行受力分析如图4-乙所示,根据牛顿第二定律可知mgsin30°＝ma,解得物体A 沿斜面下滑的加速度此时虽然物体A、斜面加速度不同,但题目需要计算台秤对整体的支持力,因此也可以将二者作为整体对竖直方向进行受力分析,如图4-丙所示,根据牛顿第二定律可得(M ＋m)g－FN2＝M×0＋masinθ,解得

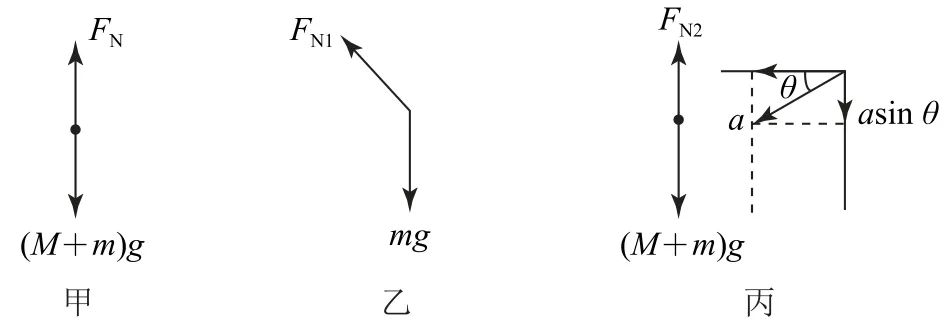
图4

根据牛顿第三定律可知,此时台秤的示数即整体对台秤的压力大小为比开始的压力(M ＋m)g 减小了选项 D 正确.

【点悟】对各物体加速度不相同的系统来说,我们一般会用隔离法处理.但对于一些复杂问题,单用隔离法很难求出结果,解决过程也比较烦琐,甚至用隔离法无从下手.这时,我们不妨试用一下整体法.这种情况下,在定量计算时,一般既要分解力,也要分解加速度,所以牛顿第二定律的表达式

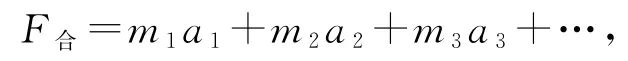
一般写成如下分表达式:

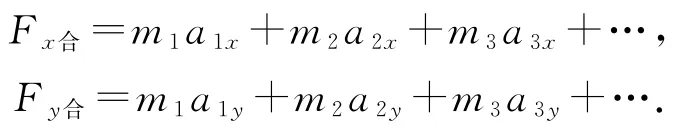
综上所述,在分析多个物体相互作用的问题时,认真分析题意,根据题目特征,利用整体法和隔离法恰当选取研究对象,不仅能够快速找到解题的着手点,而且可以简化计算,提高解题速度.