声固耦合系统的某消声器结构性能研究

刘文瑜， 罗卫东,2

(1.贵州大学 机械工程学院， 贵州 贵阳 550025； 2.贵州大学 明德学院， 贵州 贵阳 550025)

引言

消声器是一个相对密闭的空间，它受到的激励都作用于壳体，这种激励会引发壳体振动从而产生辐射声，声波的波动又会引起消声器内部空气振动，两者互相影响放大或衰减原壳体的振动，这种结构与声腔的相互作用，就形成了声固耦合系统。

赵荣宝等[1]总结了前人对统计能量、传递分析、模态计算等方法，还预测了结构模态分析法的趋势。徐嘉启等[2]基于模态叠加法计算了在由有声腔和结构相互影响下系统中的混响声压。姜哲[3-4]从理论推导到实例计算再到声场重构，系统的解析了声辐射问题中的模态分析过程。李双等[5]研究了结构模态和声模态之间的联系。KRUNTCHEVA M R[6]指出考虑声固耦合会改变系统的动力学特性，并研究了薄壁结构与薄壁声腔模态之间的耦合关系。马飞天等[7]用有限元分析法分析了结构-声腔耦合系统的模态特征，得出耦合系统的模态不是两个单体模态的简单叠加，且其中一个的模态振型会影响另一个系统中的模态振型。

结构在声场中的响应可以通过实验和计算进行研究，一般来说为了简化模型，都是把流体对结构的影响视为对结构附加质量，这无疑降低了精度。要贴近实际分析结构和声腔的相互作用，就必须建立声固耦合方程计算所有必要的单位矩阵和载荷矢量。本研究为了探究该消声器壳体在两者相互作用下是否会发生共振开裂，采用直接耦合法，构建了声固耦合模型，通过数值分析耦合系统的结构性能特性。

1 建立耦合模型

消声器内腔室形成一个相对封闭的声学系统，壁面结构视为弹性壁，对于弹性薄壁的声振耦合分析，由于壳体周围存在流体介质，在结构和流体之间存在着耦合关系。由于Virtual.Lab提供节点fix功能，所以结构网格和声学网格尺寸可以不一致，考虑计算机性能，这里结构网格尺寸选为4 mm，声学网格尺寸由式(1)计算取8 mm。用Hypermesh软件划分消声器的声学网格和结构网格，同时赋予壳体材料属性，消声器壳体材料属性如表1所示。

(1)

式中,λ—— 网格尺寸

C0—— 声在理想空气中的速度

fmax—— 计算的最大频率，取3000 Hz

导入Virtual.Lab中使用检查节点冲突功能把2个网格节点匹配起来，得到耦合模型如图1所示。

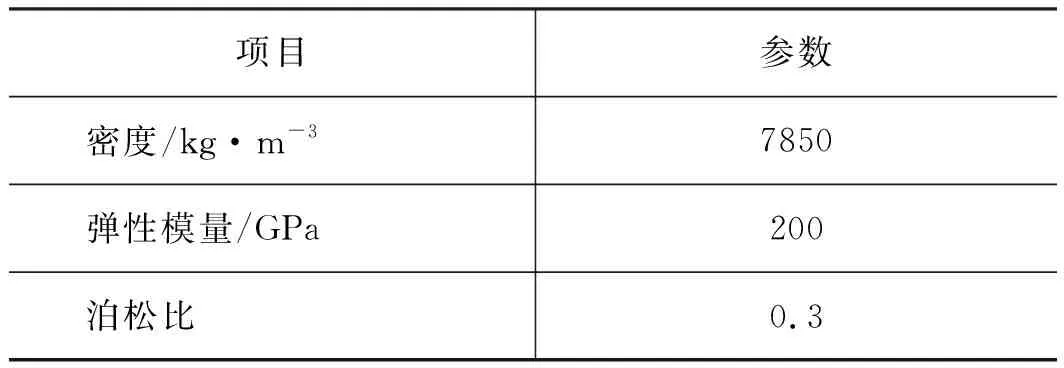
表1 消声器材料属性

图1 结构、声学、耦合模型

2 模态分析

2.1 结构模态分析

模态是物体固有的特征，外界激励对之影响微乎其微。一般地，理想条件下忽略系统阻尼和外界载荷，多自由度振动系统运动微分方程[8-9]为：

(2)

式中, [Ms] —— 系统的质量矩阵

[Ks] —— 系统的刚度矩阵

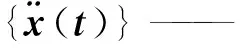
{x(t)} —— 系统的节点位移向量

{x(t)}={A}sinωt

(3)

式中, {A} —— 模态振型向量

ω—— 某一阶模态频率

把式(3)代入式(2)可得：

([Ks]-ω2[Ms]){A}=0

(4)

当|[Ks]-ω2[Ms]|=0时，求出的ω2就是特征值，开方就可得到各阶次的模态频率。

图2 约束位置

该消声器在安装的时候有螺栓连接，所以在计算时应添加相应的约束条件，约束位置如图2所示。经理论计算后再由Virtual.Lab计算出该消声器的前8阶模态固有频率及振型，振型图如图3所示，振型特征和最大变形位置如表2所示。从图3和表2中可以看到该消声器的理论计算和仿真结果误差不超过0.6%，表明计算结果是正确可靠的。

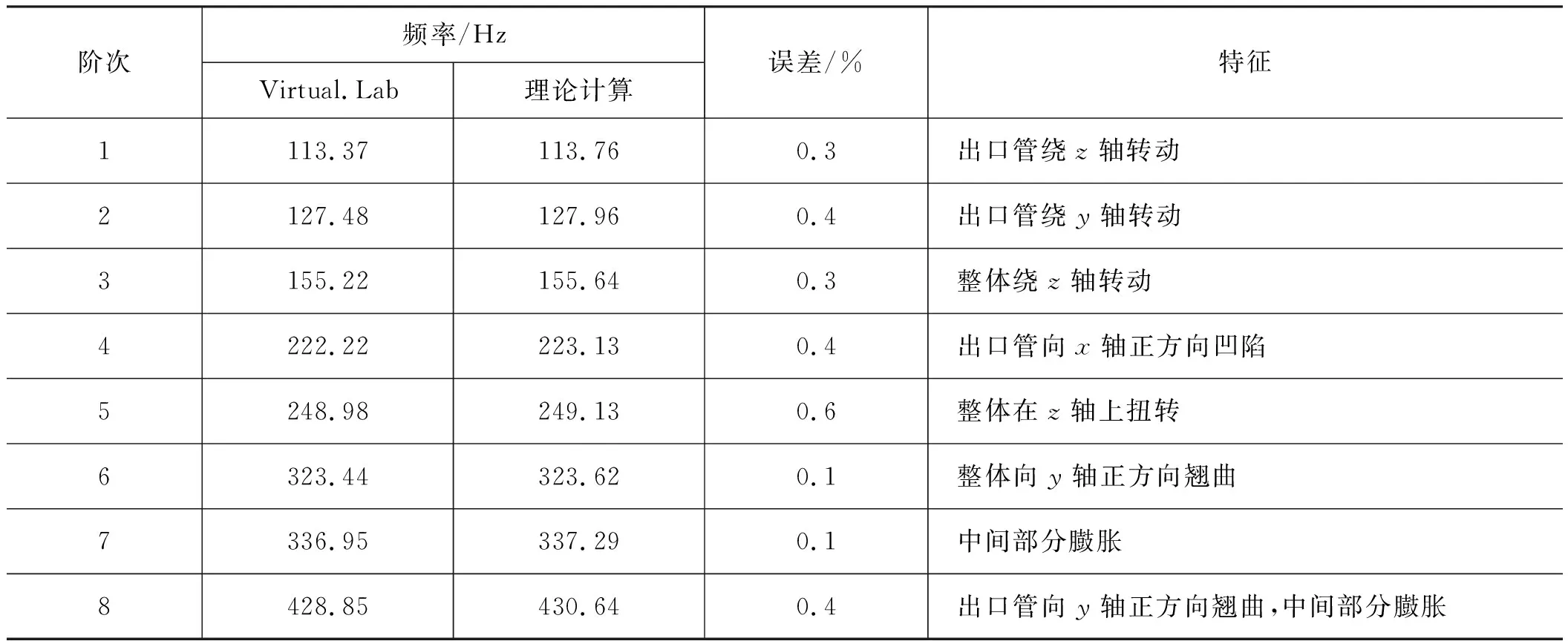
表2 结构模态前8阶振型特征

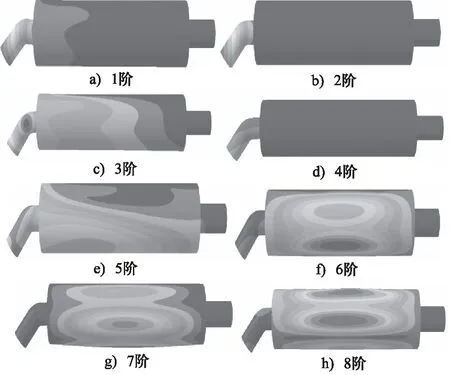
图3 前8阶结构模态振型

2.2 声模态分析

声腔模态的振型特征表现为某一频率下扩张腔内部不同位置的声压分布。理想状态下，把声波传递视为无衰减，所以理想流体介质无衰减声学波动方程[10]为：

(5)

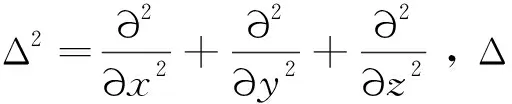
结合声学边界条件，用离散法求解式(5)，可得流体矩阵方程[11]：

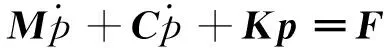
(6)

式中,M—— 声学质量矩阵

C—— 声学阻尼矩阵，由于是声波传递无衰减，所以取0

K—— 声学刚度矩阵

p—— 节点声压矢量

F—— 载荷矢量

声学模态分析是对F=0时计算其特征值和特征向量。进一步写为：

(K-ω2M)p=0

(7)

式中,ω为声学模态频率。

特征方程为：

|K-ω2M|=0

(8)

式(8)可以求出声模态频率ωi(i=1,2,3,… )，将模态频率代入式(7)即可求出声压振型pi(i=1,2,3,… )。

利用Virtual.Lab声学有限元模块设置进口处振动速度1 m/s，计算前10阶声学模态，从第1阶到第8阶对应的频率为：0, 191.1, 352.1, 432.1, 521.3, 652.0, 835.6, 961.0, 962.3, 988.7 Hz。列出某些阶次振型图如图4所示。

由图4可以看到，消声器声腔的横、纵模态十分明显，1阶振型可以忽略，2到7阶呈现的都是纵向模态，由于扩张腔是对称的，所以声压分布也较为均匀，且峰值出现在352.1 Hz的出口端。随着频率的提高可以看到在第8阶首次出现了横向模态，对称线在X轴上。在第10阶时出现了横向模态和纵向模态，说明在988.7 Hz时声传播在扩张腔内反应比较剧烈，可能会发生共振开裂。

图4 各阶次声模态振型图

2.3 耦合模态分析

对于消声器结构建立运动微分方程：

(9)

式中,M1—— 结构质量矩阵

K1—— 结构刚度矩阵

F1—— 结构外载荷矢量

u—— 偶合面上节点的位移矢量

建立声学有限元方程为：

(10)

式中,M2—— 声学质量矩阵

K2—— 声学刚度矩阵

F2—— 边界条件决定的单位表面传给流体的力矢量

所以耦合方程[12]可以写成：

(11)

式中,S—— 耦合矩阵

c—— 声在理想空气中的速度

ρ—— 理想空气密度

基于此理论用直接声固耦合法在软件里计算前8阶耦合模态，观察耦合系统中的消声器模态变化，表3列出了耦合模态的频率和振型特征，将耦合模态振型制成如图5所示。

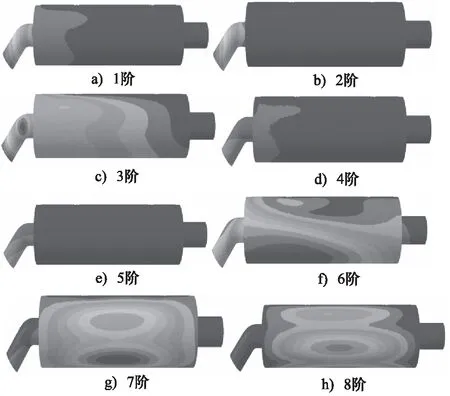
图5 前8阶耦合模态振型

从表3中可以看到：耦合系统中结构和声腔相互影响，前3阶耦合系统频率相比单独结构系统变化不大，4到8阶都有一定幅度的降低，更易发生共振；只有第3阶模态振型特征从整体绕z轴转动变成了出口管绕z轴转动，说明耦合系统中空气对以结构变形为主的振型特征影响并不大。从图5中可以看到：变形分布有些许变动，但总体趋势没有变化，这是由于结构振动引起的声压变化或者声压变化引起的结构振动导致的；各阶最大变形量在数值上有所增加，但增加量不大，平均约为0.6 mm。

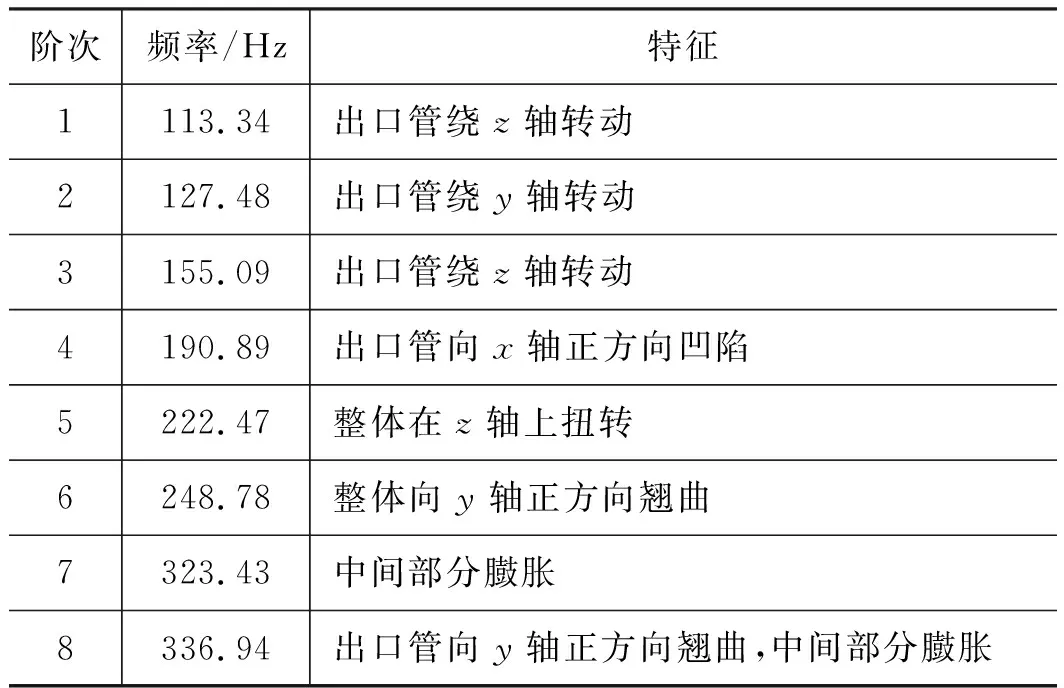
表3 耦合模态振型

3 共振分析

车辆在运行时，路面激励和发动机激励是排气系统受到的主要激励。但随着国家的发展与进步，道路情况越来越好，路面越来越平坦，此时的路面激励比较小，可以忽略，主要研究的是在发动机激励下该消声器壳体耦合系统是否会发生共振导致壳体开裂。

本研究的车辆装载CMI ISF2.8s4129v型号发动机，4缸4冲程，额定转速为3200 r/min，发动机常用工作转速为800≤n≤ 3200 r/min，内燃机动力学的发动机激励[13]可以由式(12)表示：

(12)

式中,n—— 转速

z—— 缸数

τ—— 冲程数

求得发动机激励频率范围为26.67 Hz≤f≤106.67 Hz，结合表3可知，发动机最大激励106.67 Hz小于声固耦合系统的1阶固有频率113.34 Hz，数值为6.67 Hz，声固耦合系统动态性能较好，壳体不会因共振而开裂。但如果路面情况比较差，在路面和发动机共同激励下还是可能会发生共振，路面激励计算公式[14]为：

(13)

式中,v—— 行驶速度

λ—— 路面不平度波长，这是由路面情况决定的

4 结论

用理论计算和Virtual.Lab仿真分析某消声器的结构模态，通过对比验证仿真结果的正确性，在Virtual.Lab中建立了声固耦合模型，经过仿真分析得出以下结论：

(1) 理论计算结果和Virtual.Lab计算结果误差未超过0.6%，证明Virtual.Lab的计算结果是可靠的；

(2) 耦合系统模态不是简单的独立模态系统叠加，2个独立模态系统相互影响，其中一个系统在模态频率处振动会引起另一个系统产生振动，二者的相互作用就会影响原系统的模态频率和振型特征；

(3) 耦合系统中空气对以结构变形为主的振型特征影响不大，但会改变其变形量；

(4) 经计算，该耦合系统1阶固有频率为113.34 Hz，不会和发动机激励106.67 Hz发生共振而导致结构开裂，结构性能较好。