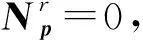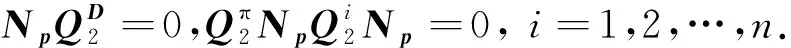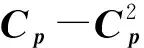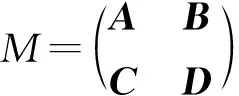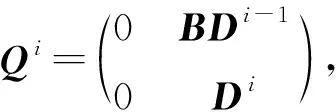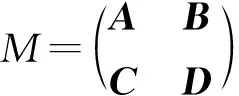关于复数矩阵的强-Drazin逆
张维玺,郭世乐,陈焕艮
(1. 杭州师范大学理学院,浙江 杭州 311121; 2. 福建技术师范学院电子与信息工程学院,福建 福清 350300)
在本文中,Cn×n表示所有n×n复矩阵的集合,N(Cn×n)表示所有n×n幂零复矩阵的集合.A∈Cn×n的Drazin逆是一个唯一的复矩阵X,表示为AD,并且满足AX=XA,X=XAX与A-A2X∈N(Cn×n).谱矩阵Aπ表示I-AAD,对任一个有Drazin逆的复数矩阵A∈Cn×n.一个复矩阵A∈Cn×n有强-Drazin逆,如果存在一个n×n的矩阵X满足X2A=X,AX=XA,A-AX∈N(Cn×n).这里X是唯一的,并且称为A∈Cn×n的强-Drazin逆.许多作者研究了强-Draizn逆,如文[1-2].正如我们所知,A∈Cn×n具有强-Drazin逆当且仅当复矩阵A可表示为可交换的幂零矩阵和幂等矩阵的和[3].
1 加性结果
本节的目的是确定两个复强-Drazin可逆矩阵和的强-Drazin逆的存在性.为了进一步讨论,先讨论如下引理.
引理1令A∈Cn×n,那么以下条件等价:
1)A有强-Drazin逆;
2)A-A2是幂零元;
3)A=E+W,这里E∈Cn×n是幂等元,W∈Cn×n是幂零元,并且EW=WE.
证明2)⟺3).由[3,引理2.1]可证,这两个条件等价.
1)⟹3).设矩阵X是复矩阵A的强-Drazin逆,由强-Drazin逆的定义可知,AX是幂等元,A-AX是幂零元,并且A=AX+A-AX,AX(A-AX)=(A-AX)AX.
3)⟹1).令X=(A+1-E)-1E,容易证明矩阵X就是复矩阵A的强-Drazin逆.
□
定理1令P,Q∈Cn×n都有强-Drazin逆,并且PQiP=0,i=1,2,…,n.那么P+Q有强-Drazin逆.
证明因为P,Q∈Cn×n都有强-Drazin逆,所以存在正整数n,m使得(P-P2)n=0, (Q-Q2)m=0.我们需要证明(P+Q)-(P+Q)2是幂零元.
(P+Q)-(P+Q)2=(P-P2)-QP+(Q-Q2)-PQ.
首先证明(P-P2)-QP和(Q-Q2)-PQ都是幂零元.因为PQiP=0,i=1,2,…,n,所以由归纳法可得
((P-P2)-QP)n+1=(P-P2)n+1-QP(P-P2)n=0.
然后,((Q-Q2)-PQ)2m的每一项可以写成如 (Q-Q2)i1(PQ)j1(Q-Q2)i2(PQ)j2…(Q-Q2)ik(PQ)jk的形式,其中i1+j1+i2+j2+…+ik+jk=2m.因为PQiP=0,i=1,2,…,n.那么这些项又可以写成
(Q-Q2)iPQ(Q-Q2)j,i+j=2m-1.
由于(Q-Q2)iPQ(Q-Q2)j=0,所以((Q-Q2)-PQ)2m=0.
现在证明(P-P2)-QP+(Q-Q2)-PQ是幂零元.令A=(P-P2)-QP,B=(Q-Q2)-PQ,那么有An+1=0,B2m=0.设f(λ)=λn-a1λn-1-…-an为Q的特征值多项式.由Cayley-Hamilton定理可得f(Q)=0.因此Qn=a1Qn-1+…+anI.因为PQiP=0,i=1,2,…,n,所以有PQiP=0对任意正整数k,进一步可得ABkA=0 对任意正整数k.显然,(A+B)n+4m+2的每一项可以写成
Ar1Bs1Ar2Bs2…ArkBsk,r1+r2+…+rk+s1+s2+…+sk=n+4m+2,
并且ri 情况Ⅰr1=0,那么上述式子的每一项可以写成如Bs1Ar2Bs2…ArkBsk的形式,其中s1<2m,r2 情况Ⅱr1>0,有r1 因此,有(A+B)n+4m+2=0,所以A+B是幂零元.证毕. 推论1令P,Q∈Cn×n都有强-Drazin逆,并且PQP=0,PQ2=0,那么P+Q有强-Drazin逆. 证明因为PQP=0,PQ2=0,所以有PQiP=0,i=1,2,…,n.因此,由定理1,可证得P+Q有强-Drazin逆. 本节的目标是将上文结果应用于分块复数矩阵.我们现在推导: 因为CAiB=0,i=1,2,…,n,由Cayley-Hamilton定理可得,CAiB=0,i=1,2,…,2n,因此PQiP=0,i=1,2,…,2n.所以,由定理1,可得P+Q有强-Drazin逆.证毕. 众所周知,1994年,美国数学家约翰·纳什、约翰·海萨尼、莱因哈德·泽尔腾因在非合作博弈均衡分析理论方面做出了开创性贡献,从而对博弈论和经济学产生了重大影响,而共同获得诺贝尔经济学奖。这一当今科学界最有影响力的奖项颁发,充分说明了数学对经济的重要性。财经与数学息息相关,现在经济学大多是要求有计量经济模型分析的,计量经济学的支持就是数学;博弈论的也是依靠数学思维分析,……。这也就不难理解,许多财经类企事业单位和科研机构在招聘时甚至会直接录用数学专业或有数学专业背景的学生。可见,一方面是数学是财经类行业的重要的工具;另一方面,数学思维对财经类行业有重要指导意义。 令P∈Cn×n有强-Drazin逆,那么它就有Drazin逆.下文用Pπ表示谱幂等元In-PPD.现在证明: 定理3令P,Q∈Cn×n都有强-Drazin逆,并且PQD=0,PDQ=0,QπPQiPPπ=0,其中i=1,2,…,n,那么P+Q有强-Drazin逆. 证明因为P,Q∈Cn×n都有强-Drazin逆,由强-Drazin逆的定义可知,若某元素的强-Drazin逆存在,那么它与该元素的Drazin逆是相同的.假设ind(P)=r.由[4,引理1]可得 也有强-Drazin逆由于P+Q-(P+Q)2是幂零元. 推论2令P,Q∈Cn×n都有强-Drazin逆,并且PQD=0,PDQ=0,QπPQPPπ=0,QπPQ2Pπ=0,那么P+Q有强-Drazin逆. 证明因为QπPQ2Pπ=0且PDQ=0,有 QπPQ2PPπ=0,QπPQ3Pπ=QπPQ2PπQPπ+QπPQ2PPDQPπ=0. 那么可得QπPQ3PPπ=0,由归纳法容易证明QπPQiPPπ=0,i=1,2,…,n.因此,由定理3,证毕. 因此 作为直接结论,可得: 证明因为CB=0,有CBDiCAπ=0,i=0,1,…,n-1,那么由定理4,可证得结果.
2 分块矩阵
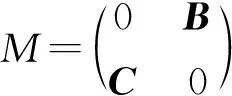
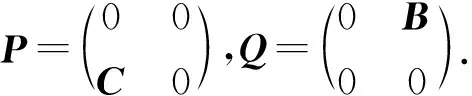
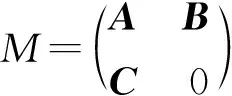
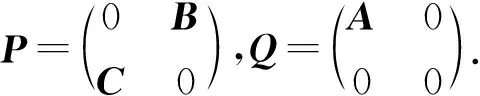
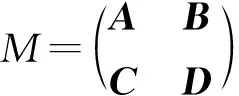

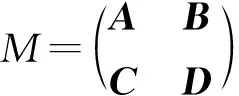

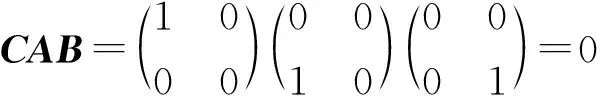
3 谱条件