一类平面脉冲系统的稳定性与相图研究

李路遥，申建华

(杭州师范大学理学院，浙江 杭州 311121)

0 引言

任意一个二维常系数线性微分系统u′=Au,其中A为非退化的常数矩阵，经过适当的坐标变换之后，就可以转化成3种标准形式之一.本文讨论如下标准形式的脉冲系统：

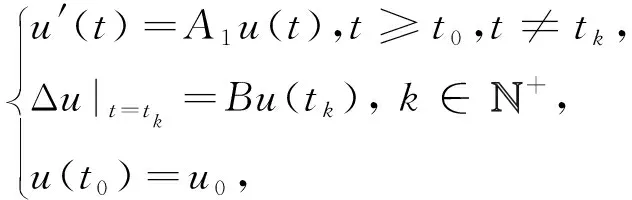
(1)

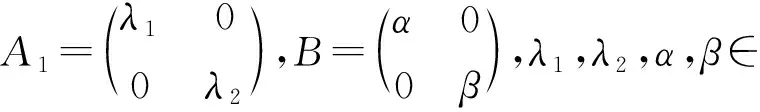
近年来，关于脉冲微分方程的研究已有较多深刻结果[1-7]，但有关脉冲微分方程几何理论的研究还不多，主要困难是不连续动力系统的相空间理论还不完善.本文旨在研究系统(1)的稳定性和相图特征，得到的结果显示系统(1)有比系统u′(t)=A1u(t) 更加复杂的动力学性质.

1 主要结果

经过计算，不难得到系统(1)的解为

(2)

其中i=1,2,u1=x,u2=y,σ1=α,σ2=β,u01=x0,u02=y0.为了得到系统(1)更加复杂的相图特征，需要引入一个引理，由于证明过程较为简单，这里不做证明.

令Sk={(xk(t),yk(t))|xk=(1+α)k-1x0eλ1(t-t0),yk=(1+β)k-1y0eλ2(t-t0),k=1,2,3,…}, 则{Sk}是曲线族.事实上，系统(1)的相图在曲线族{Sk}上.

若1+α=0或1+β=0，当t>t1,x(t)=0，或y(t)=0，系统(1)的相图在y-轴或x-轴上.因此，仅需考虑下列两种情形：Ⅰ)α>-1,β>-1；Ⅱ)α>-1,β<-1，或α<-1,β>-1，或α<-1,β<-1.

对于情形Ⅰ，容易得到

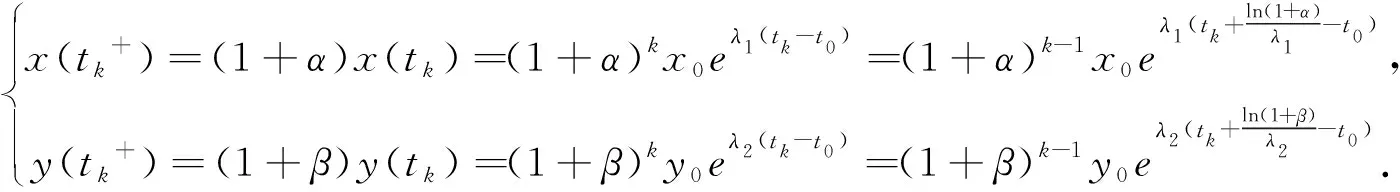
(3)

从而可以看出，点(x(tk+),y(tk+))和曲线Sk在同一象限上，且(x(tk+),y(tk+))在曲线Sk+1上.因此，曲线Sk和Sk+1在同一象限内.由于xk(t),yk(t)都是关于t的单调函数，从而由引理1知：

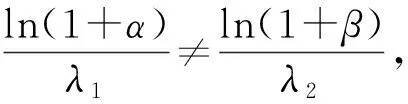
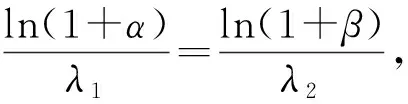
(4)

此时，对系统(1)相图的特征及解的稳定性，有以下结论.

定理1对系统(1)有：

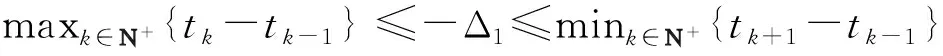
3) 当Δ1>0时，系统(1)的相图是间断连续的，且λ1<0,λ2<0时，系统(1)的解是渐近稳定的；当λ1>0,λ2>0时，系统(1)是无穷扩散的.

(5)

当λ1<0，可得

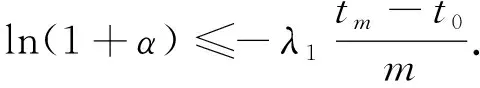
(6)

(7)

于是，当m→+∞时，

因此，当m→+∞时有x(t)→0.同理可得，当λ2<0时，y(t)是有界的，而且y(t)→0.从而当λ1<0,λ2<0时系统(1)是渐近稳定的.

当λ1>0，从式(5)可以得到

(8)

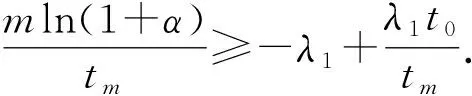
于是对∀t∈(tm,tm+1]，当m→+∞时，

即x(t)→+∞(t→+∞).同理可得，当λ2>0时，有y(t)→+∞(t→+∞).从而系统(1)是无穷扩散的.

下证稳定性.由于

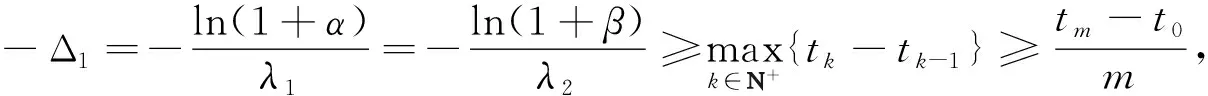
(9)

类似于1)的证明，可以得到当λ1>0,λ2>0时，系统(1)是渐近稳定的.当λ1<0,λ2<0时，系统(1)是无穷扩散的.

3) Δ1>0，由于tk+Δ1>tk，系统(1)在任意两个相邻区间(tk,tk+1]和(tk-1,tk]上没有重叠部分，因此相图间断连续.下证稳定性.由于

所以，当λ1<0,λ2<0,ln|1+α|<0,ln|1+β|<0时，有

当λ1>0,λ2>0,ln|1+α|>0,ln|1+β|>0时，有

所以，当λ1<0,λ2<0时，系统(1)是渐近稳定的.当λ1>0,λ2>0时，系统(1)是无穷扩散的.

(10)

可以看出点(x(tk+),y(tk+))和曲线Sk不在同一象限，但与曲线Sk-1在同一象限，这也说明曲线Sk+1与曲线Sk不在同一象限，但与曲线Sk-1在同一象限.由于xk(t),yk(t)都是关于t的单调函数，从而由引理1知：

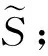
(11)

此时，对系统(1)相图的特征及解的稳定性，有以下结论.

定理2对系统(1)有：

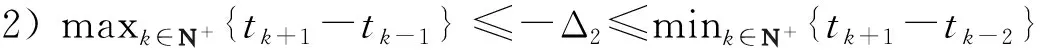
系统的热容Ct是热水器的固有属性，文献[7]中通过实验数据的样本点进行最小二乘法的拟合并通过线性回归进行校核分析，得到的最终待定系数Ct的取值为21.7～25.3 kJ/K。在此，将热水温升与加热时间的数学模型导入MATLAB软件进行模拟计算，系统热容Ct以2为步长进行划分，其余参数取均值且保持不变，具体参数见表1，热水温升与加热时间的关系曲线如图3所示。

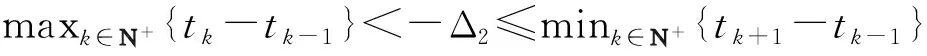
于是有

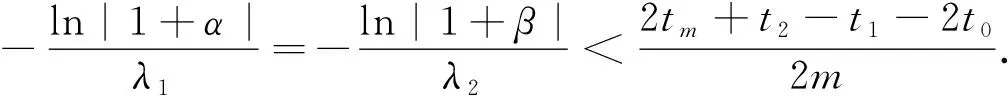
(12)

当λ1<0时容易得到

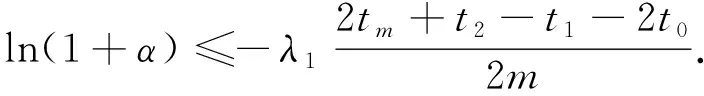
(13)

因此

从而

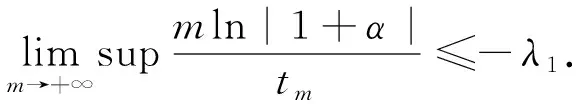
(14)

因此x(t)→0(t→+∞).同理可得，当λ2<0时，y(t)→0(t→+∞).从而系统(1)是渐近稳定的.当λ1>0，从式(13)可得

(15)

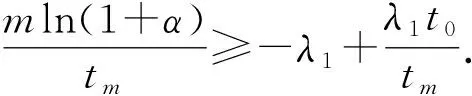
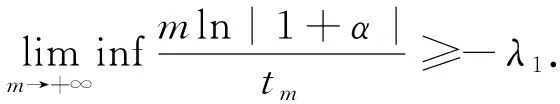
(16)

即x(t)→+∞(t→+∞).同理可得，当λ2>0时，有y(t)→+∞(t→+∞).从而系统(1)是无穷扩散的.

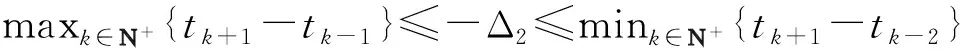
于是有

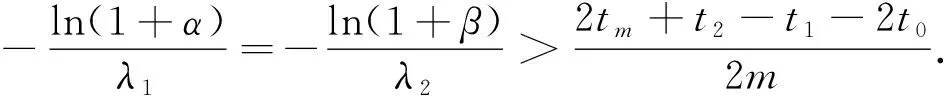
(17)

因此，类似1)的证明，可以得到以下结论：当λ1>0,λ2>0时，系统(1)是渐近稳定的；当λ1<0,λ2<0时，系统(1)是无穷扩散的.

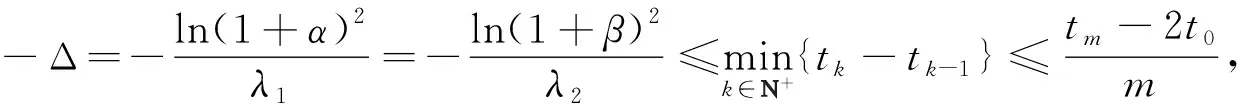
(18)

于是有

因此，可以得到以下结论：当λ1<0,λ2<0时，

当λ1>0,λ2>0时，

所以当λ1<0,λ2<0时，系统(1)是渐近稳定的；当λ1>0,λ2>0时，系统(1)是无穷扩散的.

2 数值模拟

下面仅给出当λ1<0,λ2<0时的数值模拟.

对于情形Ⅰ，当α>-1,β>-1时，取定参数λ1=-0.6,λ2=-0.3,x0=100,y0=120,tk=5k.

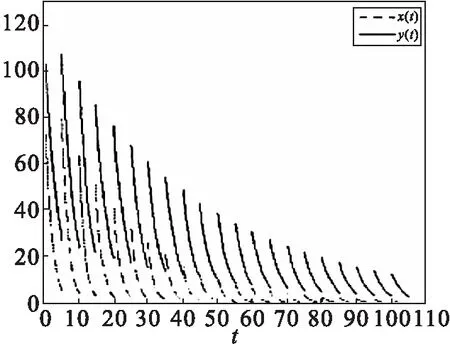
(a)函数图

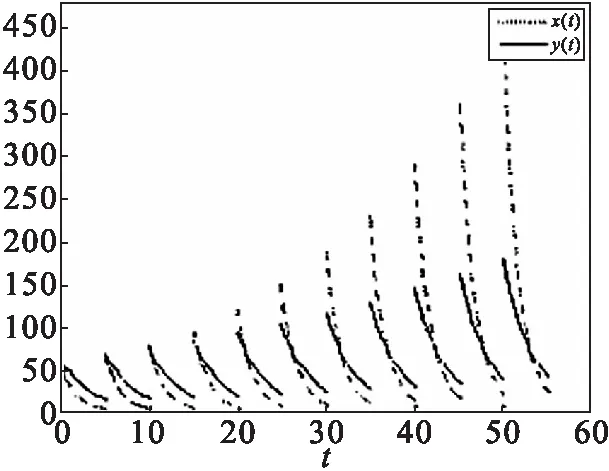
(a)函数图

由图1、2可以看出系统(1)是渐近稳定的，且此时相图在整个区间上看起来是连续的，但实际是间断连续的.

3) 当Δ1>0时，取α=-0.36,β=-0.2，得到的函数图和相图见图3.

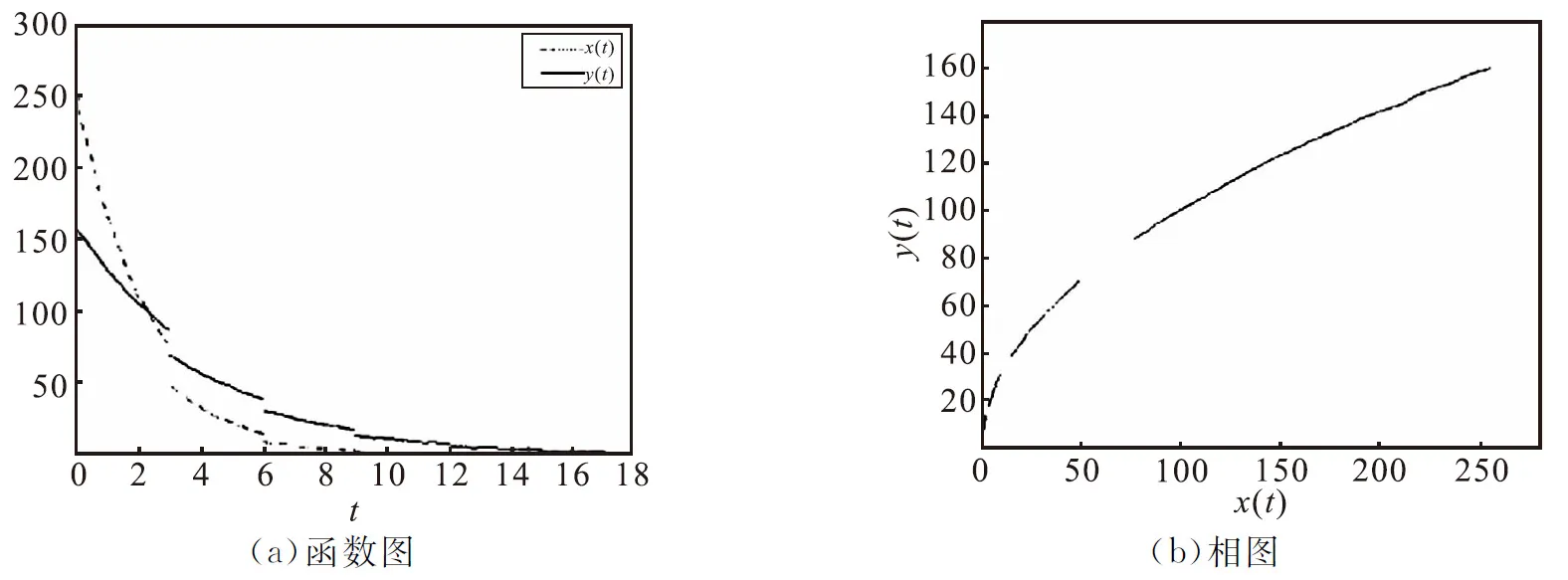
由图3可以看出系统(1)是渐近稳定的，且此时相图在整个区间上明显是间断连续的.

考虑情形Ⅱ，即α>-1,β<-1，或α<-1,β>-1，或α<-1,β<-1.

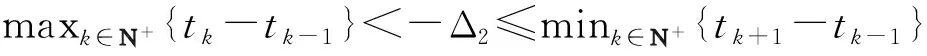
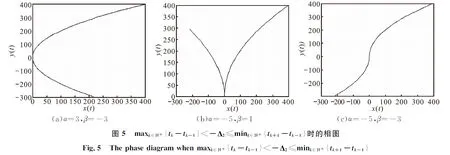
从图4可以看出系统(1)是渐近稳定的，从图5可以看出相图在整个区间上看起来是连续的，但实际上是间断连续的.

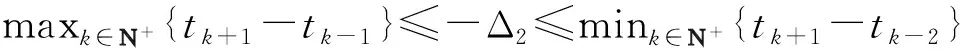
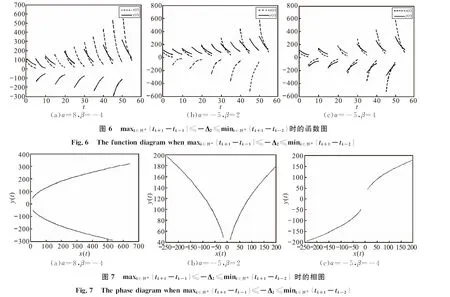
从图6可以看出系统(1)是无穷扩散的，从图7可以看出相图在两个象限上看起来是连续的，但其实是间断连续的.

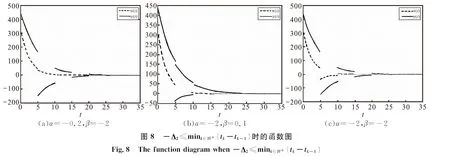
但在不同象限的相图见图9.

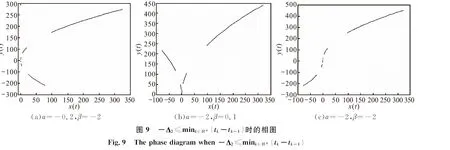
由图8、图9可以发现，系统(1)是渐近稳定的，而且相图明显是间断连续的.